Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 4 દ્વિચલ સુરેખ સમીકરણો
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 4 દ્વિચલ સુરેખ સમીકરણો
સ્વાધ્યાય – 4.1
1. “નોટબુકની કિંમત પેનની કિંમત કરતાં બમણી (બે ગણી) છે.’ આ વિધાનને દ્વિચલ સુરેખ સમીકરણ સ્વરૂપે દર્શાવો. (નોટબુકની કિંમત ₹ x તથા પેનની કિંમત ₹ y લો.)
ધારો કે, નોટબુકની કિંમત ₹ x તથા પેનની કિંમત ₹ y છે.
આપેલ માહિતી મુજબ નોટબુકની કિંમત પેનની કિંમત કરતાં બમણી છે.
∴ x = 2y
આમ, x = 2y, એટલે કે, x – 2 = 0 એ માગેલ દ્વિચલ સુરેખ સમીકરણ છે.
2. નીચે દર્શાવેલા દ્વિચલ સુરેખ સમીકરણોને ax + by + c = 0 તરીકે દર્શાવો અને દરેક કિસ્સામાં a, b અને ની કિંમત શોધો :
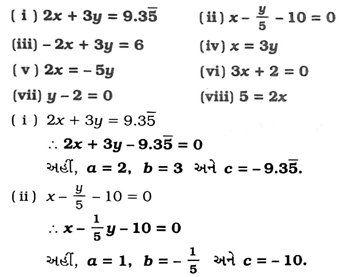
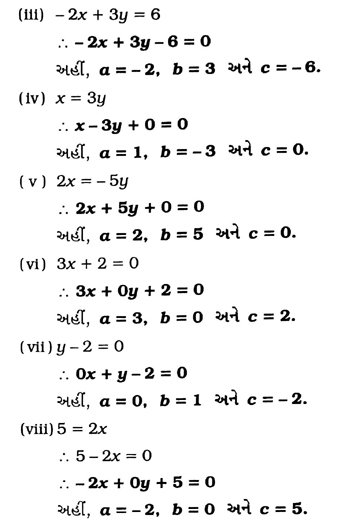
સ્વાધ્યાય – 4.2
1. નીચેના પૈકી કયો વિકલ્પ સાચો છે અને શા માટે?
y = 3x + 5ને (i) અનન્ય ઉકેલ હોય. (ii) માત્ર બે ઉકેલ હોય. (iii) અનંત ઉકેલ હોય.
વિકલ્પ (iii) એ સાચો વિકલ્પ છે. y = 3x + 5 એ દ્વિચલ સુરેખ સમીકરણ હોવાથી તેને (1, 8), (2, 11), (3, 14), (4, 17), (0, 5), (– 1, 2) જેવાં અનંત ઉકેલ હોય.
2. નીચેના પૈકી પ્રત્યેક સમીકરણના ચાર ઉકેલ લખો :
(i) 2x + y = 7
(ii) πx + y = 9
(iii) x = 4y
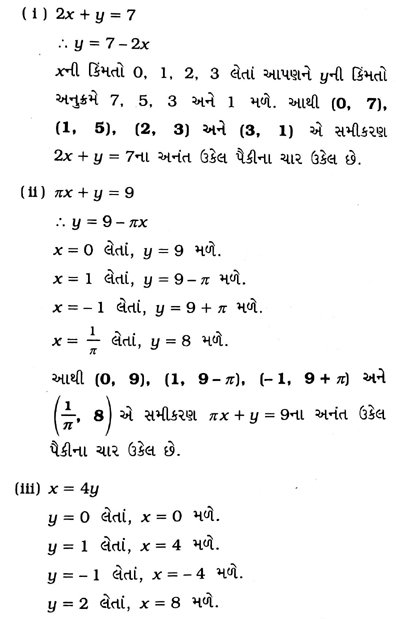
આથી (0, 0), (4, 1), (−4, −1) અને (8, 2) એ સમીકરણ x = 4y ના અનંત ઉકેલ પૈકીના ચાર ઉકેલ છે.
3. નીચેનામાંથી કાં બિંદુઓ સમીકરણ x – 2y = 4ના ઉકેલ છે અને કયાં બિંદુઓ ઉકેલ નથી તે ચકાસો :

4. જો x = 2, y = 1 એ સમીકરણ 2x + 3y = ત્નો એક ઉકેલ હોય, તો પત્ની કિંમત શોધો.
x = 2, y = 1 એ સમીકરણ 2x + 3y = kનો એક ઉકેલ છે. આથી x = 2 અને y = 1 દ્વારા સમીકરણનું સમાધાન થાય.
∴ 2 (2) + 3 (1) = k
∴ 4 + 3 = k
∴ 7 = k
∴ k = 7
સ્વાધ્યાય – 4.3
1. નીચે દર્શાવેલા પ્રત્યેક દ્વિચલ સુરેખ સમીકરણ માટે આલેખ દોરો :
(1) x + y = 4
(ii) x – y = 2
(iii) y = 3x
(iv) 3 = 2x + y
(i) x + y = 4
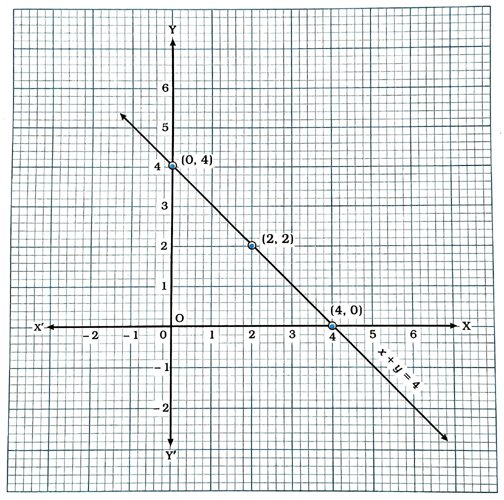
x + y = 4નો આલેખ દોરવા આપણને તેનાં ઓછામાં ઓછા બે ઉકેલ જોઈએ. સહેલાઈથી જોઈ શકાય છે કે (0, 4) અને (4, 0) એ આપેલ સમીકરણના બે ઉકેલ છે જ. પરંતુ, ચોકસાઈના હેતુથી આપણે ત્રણ ઉકેલ મેળવીશું.
x = 0 લેતાં, 0 + y = 4, એટલે કે y = 4 થાય.
x = 2 લેતાં, 2 + y = 4, એટલે કે y = 2 થાય.
x = 4 લેતાં, 4 + y = 4, એટલે કે y = 0 થાય.
આ ત્રણ ઉકેલને આપણે નીચે દર્શાવેલ કોષ્ટકમાં બતાવી શકીએ :
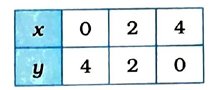
હવે, આ ત્રણ બિંદુનું કાર્તેઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ સમીકરણ x + y = 4નો આલેખ છે.
(ii) x – y = 2
x – y = 2નો આલેખ દોરવા આપણે તેના ત્રણ ઉકેલ શોધીશું. સરળતા ખાતર આપણે સમીકરણને y-સ્વરૂપમાં દર્શાવીશું, એટલે કે સમીકરણ y = x – 2 લઈશું.
x = 0 માટે, y = – 2.
x = 2 માટે, y = 0.
x = 4 માટે, y = 2.
કોષ્ટક સ્વરૂપે આ ત્રણ ઉકેલ નીચે મુજબ દર્શાવાય :
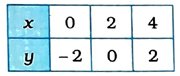
હવે, આ ત્રણ બિંદુનું કાર્તેઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ સમીકરણ x – y = 2નો આલેખ છે.
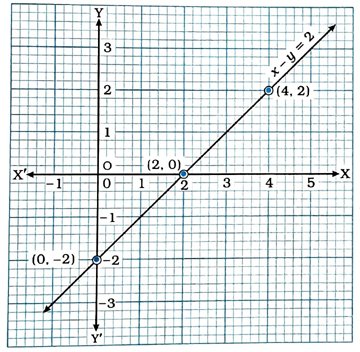
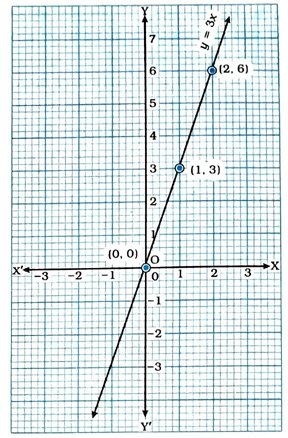
(iii) y = 3x
y = 3x નો આલેખ દોરવા આપણે તેના ત્રણ ઉકેલ શોધીશું.
x = 0 માટે, y = 0.
x = 1 માટે, y = 3.
x = 2 માટે, y = 6.
કોષ્ટક સ્વરૂપે આ ત્રણ ઉકેલ નીચે મુજબ દર્શાવાય :
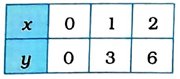
હવે, આ ત્રણ બિંદુનું કાઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ સમીકરણ y = 3x નો આલેખ છે.
(iv) 3 = 2x + y
3 = 2x + yનો આલેખ દોરવા આપણે સમીકરણને
y = 3 – 2x સ્વરૂપે દર્શાવીને તેના ત્રણ ઉકેલ શોધીશું.
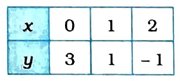
x = 0 માટે, y = 3.
x = 1 માટે, y = 1.
x = 2 માટે, y = −l.
કોષ્ટક સ્વરૂપે આ ત્રણ ઉકેલ નીચે મુજબ દર્શાવાય :
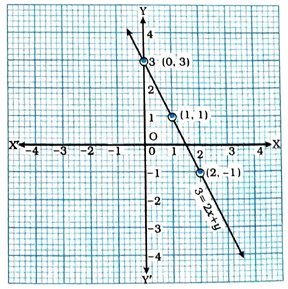
હવે, આ ત્રણ બિંદુનું કાર્તેઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ સમીકરણ 3 = 2x + yનો આલેખ છે.
2. બિંદુ (2, 14)માંથી પસાર થતી બે રેખાઓનાં સમીકરણો આપો. આવી બીજી કેટલી રેખાઓ મેળવી શકાય અને શા માટે?
બિંદુ (2, 14)માંથી પસાર થતી બે રેખાઓનાં સમીકરણ તરીકે y = 7x તથા x + y = 16 આપી શકાય. કારણ કે (2, 14) દ્વારા બંને સમીકરણોનું સમાધાન થાય છે.
આવી બીજી અસંખ્ય રેખાઓ મેળવી શકાય કે જેનું સમાધાન બિંદુ (2, 14) દ્વારા થાય. દા. ત., y – x = 12, y = 6x + 2, x – y = – 12 વગેરે. આવી અસંખ્ય રેખાઓ (સમીકરણો) મળવાનું કારણ સરળ છે. આપણે જાણીએ જ છીએ કે આપેલ સમતલમાં આપેલ બિંદુમાંથી અસંખ્ય રેખાઓ પસાર થાય છે.
3. જો બિંદુ (3, 4) સમીકરણ 3y = ax + 7ના આલેખ પરનું એક બિંદુ હોય, તો તની કિંમત શોધો.
બિંદુ (3, 4) એ સમીકરણ 3y = ax + 7ના આલેખ પરનું બિંદુ હોવાથી તેનાં યામ x = 3 અને y = 4 એ સમીકરણ 3y = ax + 7નું સમાધાન કરે.
એટલે કે, 3 (4) = a (3) + 7
∴ 12 = 3a + 7
∴ 12− 7 = 3a
∴ 5 = 3a
∴ 3a = 5
∴ a = 5/3
4. એક શહેરમાં ટૅક્સી ભાડું આ પ્રમાણે છે : પ્રથમ કિલોમીટર માટે ભાડું ₹ 8 અને ત્યારબાદના દરેક કિલોમીટર માટે ભાડું ₹ 5 પ્રતિકિલોમીટર છે. કાપેલ અંતર x કિલોમીટર અને કુલ ભાડું ₹ y લઈ આ માહિતી માટે દ્વિચલ સુરેખ સમીકરણ લખો અને તેનો આલેખ દોરો.
ધારો કે, કુલ કાપેલ અંતર x કિલોમીટર અને કુલ ભાડું ₹ y છે. હવે, પ્રથમ કિલોમીટરનું ભાડું ₹ 8 છે અને ત્યારબાદના (x – 1) કિલોમીટર માટે કિલોમીટરદીઠ ભાડું ₹ 5 છે. આથી કુલ ભાડું ₹ [8 + 5 (x – 1)] થશે, જે ₹ y આપેલ છે. આમ, આપણને નીચે મુજબનું સમીકરણ મળે :
8 + 5 (x – 1) = y
∴ 8 + 5x − 5 = y
∴ 5x – y + 3 = 0
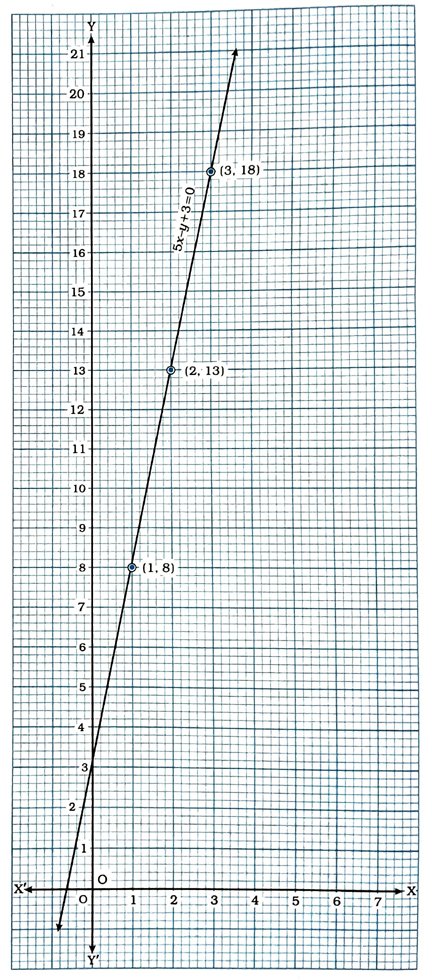
આ સમીકરણનો આલેખ દોરવા સમીકરણને y = 5x + 3 સ્વરૂપમાં દર્શાવીને તેનાં ત્રણ ઉકેલ શોધીશું.
નોંધ : કાપેલ અંતર કદી શૂન્ય અથવા ઋણ ન હોય. આથી આપણે ત્ની ધન કિંમતો જ પસંદ કરીશું.
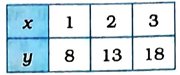
x = 1 માટે, y = 8.
x = 2 માટે, y = 13.
x = 3 માટે, y = 18.
કોષ્ટક સ્વરૂપે આ ત્રણ ઉકેલ નીચે મુજબ દર્શાવાય :
હવે, આ ત્રણ બિંદુનું કાર્તેઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ ઉપર મેળવેલ સમીકરણ 5x – y + 3 = 0 નો આલેખ છે.
5. નીચે આકૃતિ (1) અને આકૃતિ (2)માં આપેલા આલેખ માટે તેની નીચે આપેલા વિકલ્પોમાંથી યોગ્ય સમીકરણ પસંદ કરો :
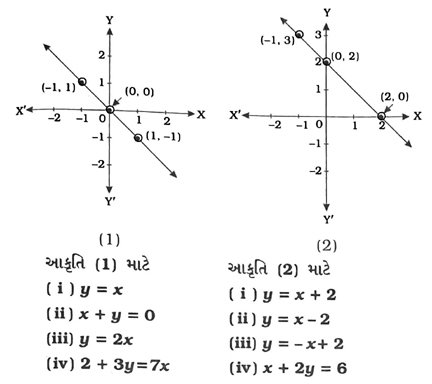
આકૃતિ (1) માટે : આકૃતિ (1)માં આપેલ આલેખ માટે યોગ્ય સમીકરણ (ii) x + y = 0 છે, કારણ કે આલેખમાં દર્શાવેલ ત્રણેય બિંદુઓ (– 1, 1), (0, 0) અને (1, −1) દ્વારા તે સમીકરણનું સમાધાન થાય છે. બાકીનાં સમીકરણો પૈકી (i) y = x તથા (iii) y = 2xનું સમાધાન બિંદુ (0, 0) દ્વારા થાય છે, પરંતુ બાકીનાં બે બિંદુઓ દ્વારા નહીં. તે જ પ્રમાણે સમીકરણ (iv) 2 + 3y = 7xનું સમાધાન એક પણ બિંદુ દ્વારા થતું નથી.
આકૃતિ (2) માટે : આકૃતિ (2)માં આપેલ આલેખ માટે યોગ્ય સમીકરણ (iii) y = – x + 2 છે, કારણ કે આલેખમાં દર્શાવેલ ત્રણેય બિંદુઓ (– 1, 3), (0, 2) અને (2, 0) દ્વારા તે સમીકરણનું સમાધાન થાય છે. સમીકરણ (i) y = x + 2નું સમાધાન માત્ર બિંદુ (0, 2) દ્વારા થાય છે. સમીકરણ (ii) y = x – 2નું સમાધાન માત્ર બિંદુ (2, 0) દ્વારા થાય છે. સમીકરણ (iv) x + 2y = 6નું સમાધાન એક પણ બિંદુ દ્વારા થતું નથી.
6. જો અચળ બળ લગાડવાથી એક પદાર્થ પર થતું કાર્ય તે પદાર્થ દ્વારા કપાયેલા અંતરના સમપ્રમાણમાં હોય, તો આ બાબતને બે ચલવાળા સમીકરણના સ્વરૂપમાં રજૂ કરો અને 5 એકમ અચળ બળ લઈ તેનો આલેખ દોરો અને આલેખ પરથી પદાર્થ દ્વારા કપાયેલ અંતર (i) 2 એકમ (ii) 0 એકમ હોય ત્યારે થતું કાર્ય શોધો.
આપણે જાણીએ છીએ કે કાર્ય = બળ × કાપેલ અંતર.
ધારો કે, કાર્ય = y અને કાપેલ અંતર = x તથા અચળ બળ = 5 એકમ છે.
તો, કાર્ય અને કાપેલ અંત૨ વચ્ચેનો સંબંધ y = 5x દ્વારા રજૂ થાય જે એક દ્વિચલ સુરેખ સમીકરણ છે.
y = 5xનો આલેખ દોરવા તેના 3 ઉકેલ શોધીને કોષ્ટક સ્વરૂપમાં દર્શાવીએ.
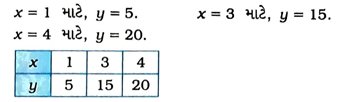
હવે, આ ત્રણ બિંદુનું કાર્તેઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ સમીકરણ y = 5ત્નો આલેખ છે.
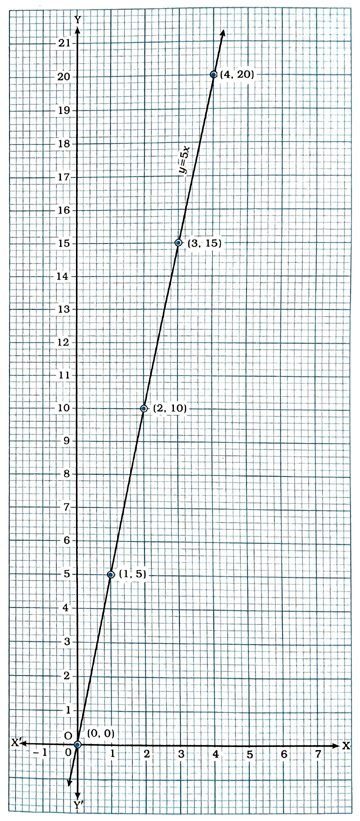
(i) આલેખ પરથી આપણે જોઈ શકીએ છીએ કે જ્યારે કાપેલ અંતર (x) 2 એકમ હોય ત્યારે થતું કાર્ય (y) 10 એકમ છે.
(ii) આલેખ પરથી આપણે જોઈ શકીએ છીએ કે જ્યારે કાપેલ અંતર (x) 0 એકમ હોય ત્યારે થતું કાર્ય (y) 0 એકમ છે.
7. ધોરણ 9ની બે વિદ્યાર્થિનીઓ યામિની અને ફાતિમાએ ભૂકંપગ્રસ્ત લોકો માટે પ્રધાનમંત્રી રાહતફંડમાં સંયુક્ત રીતે ₹ 100નો ફાળો આપ્યો. આ માહિતી આધારિત દ્વિચલ સુરેખ સમીકરણ લખો. (તમે તેમના ફાળાની રકમને ₹ x અને ₹ y લઈ શકો) આ સમીકરણ આધારિત આલેખ દોરો.
ધારો કે, યામિનીએ આપેલ ફાળો ₹ x અને ફાતિમાએ આપેલ ફાળો ₹ y છે. આથી તેમણે આપેલ કુલ ફાળો ₹ (x + y) થાય. આપેલ માહિતી મુજબ તેમણે આપેલ કુલ ફાળો ₹ 100 છે. આથી આપણને દ્વિચલ સુરેખ સમીકરણ x + y = 100 મળે. હવે, x + y = 100નો આલેખ દોરવા આપણે તેના ત્રણ ઉકેલ મેળવીએ અને તેમને કોષ્ટક સ્વરૂપે દર્શાવીએ.
x = 0 માટે, y = 100; x = 50 માટે, y = 50; x = 100 માટે, y = 0.
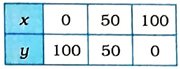
હવે, આ ત્રણ બિંદુનું કાર્તેઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ સમીકરણ x + y = 100નો આલેખ છે જે આપેલ માહિતીને રજૂ કરે છે.
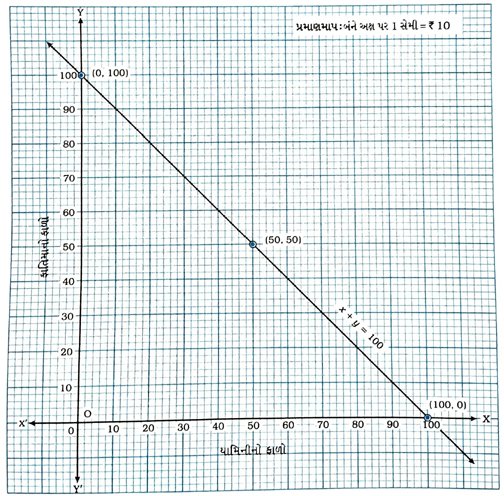
8. યુ.એસ.એ. અને કૅનેડા જેવા દેશમાં તાપમાન ફેરનહીટમાં મપાય છે. ભારત જેવા દેશમાં તાપમાન સેલ્સિયસમાં મપાય છે. અહીં ફેરનહીટનું સેલ્સિયસમાં રૂપાંતર કરતું સુરેખ સમીકરણ આપેલ છે.
(i) ઉપર દર્શાવેલ સુરેખ સમીકરણમાં ઝ-અક્ષ પર સેલ્સિયસ અને y-અક્ષ પર ફેરનહીટ લઈ આલેખ દોરો.
(ii) જો તાપમાન 30°C હોય, તો ફેરનહીટમાં શું તાપમાન થાય?
(iii) જો તાપમાન 95 °F હોય, તો સેલ્સિયસમાં તાપમાન કેટલું હોય?
(iv) જો તાપમાન 0°C હોય, તો ફેરનહીટમાં તાપમાન કેટલું હોય અને જો તાપમાન 0F માં હોય, તો સેલ્સિયસમાં તાપમાન કેટલું હોય?
(v) ફેરનહીટ અને સેલ્શિયસમાં સંખ્યાત્મક રીતે સમાન હોય તેવું તાપમાન હોય? જો હા તો તે શોધો.


સ્વાધ્યાય – 4.4
1. સમીકરણ y = 3નું (i) એક ચલમાં (ii) બે ચલમાં ભૌમિતિક નિરૂપણ દર્શાવો.
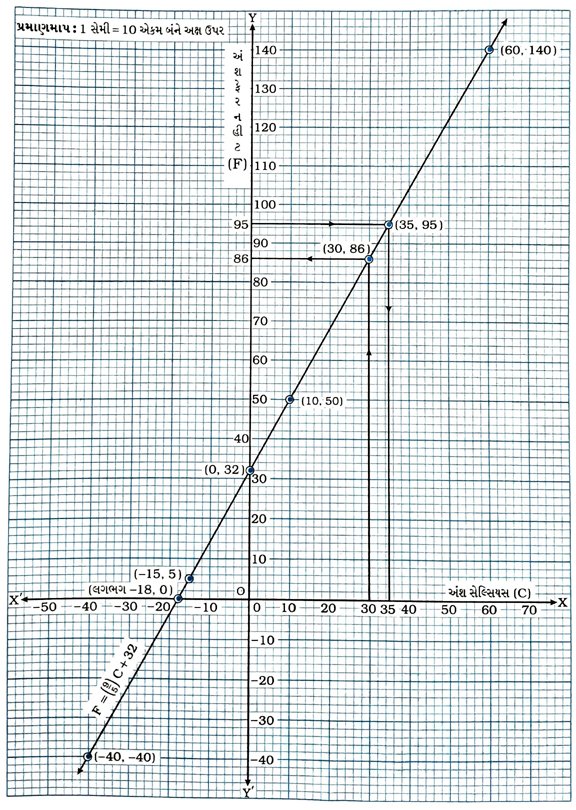
(i) સમીકરણ y = 3ને એક ચલના સમીકરણ તરીકે લેતાં તેનો આલેખ સંખ્યારેખા પર બિંદુ સ્વરૂપે હોય, જે નીચે દર્શાવેલ છે :
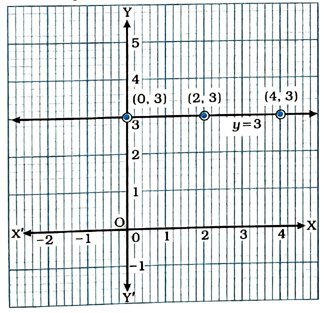
(ii) સમીકરણ y = 3ને દ્વિચલ સુરેખ સમીકરણના સ્વરૂપે 0x + y = 3 લખાય. અહીં xની કોઈ પણ કિંમત માટે yની કિંમત 3 જ થાય. આથી (0, 3), (2, 3) અને (4, 3) ને સમીકરણના ત્રણ ઉકેલ તરીકે સહેલાઈથી લઈ શકાય.
હવે, આ ત્રણ બિંદુઓનું કાર્તેઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ દ્વિચલ સુરેખ સમીકરણ y = 3નો આલેખ (નિરૂપણ) છે.
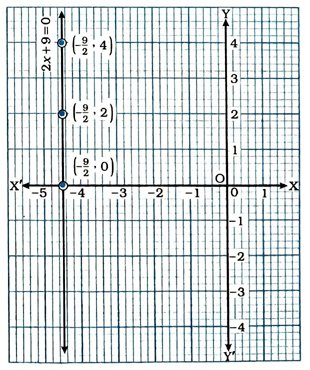
2. સમીકરણ 2x + 9 = 0નું (i) એક ચલમાં (ii) બે ચલમાં ભૌમિતિક નિરૂપણ દર્શાવો.

હવે, આ ત્રણ બિંદુઓનું કાર્તેઝિય સમતલમાં નિરૂપણ કરીને તે બિંદુઓમાંથી પસાર થતી રેખા દોરીએ. આ રેખા એ દ્વિચલ સુરેખ સમીકરણ 2x + 9 0નો આલેખ (નિરૂપણ) છે.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરો : (ફક્ત અંતિમ જવાબ)
(1) સમીકરણ 4x – 3y = 24ને પ્રમાણિત સ્વરૂપમાં ……. લખાય.
(2) 3x + 5y = k નો એક ઉકેલ (3, 3) હોય, તો k = …….. .
(3) F = (9/5) C + 32માં C = 15 હોય, તો F = …….. .
(4) 4x – ky = 20નો એક ઉકેલ (10, 4) હોય, તો k = …….. .
(5) જો 7x + 2y = k નો આલેખ ઉગમબિંદુમાંથી પસાર થતી રેખા હોય, તો k = …….. .
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) સમીકરણ 5x – 3y = 60ને પ્રમાણિત સ્વરૂપમાં લખો.
( 2 ) 2x + 5y = k નો એક ઉકેલ (3, 2) હોય, તો k ની કિંમત શોધો.
( 3 ) જો 13x + 12y = 60 અને 12x + 13y = 40 હોય, તો x + yની કિંમત શોધો.
( 4 ) સમીકરણ 3x – 4y = 12નું y-સ્વરૂપ આપો.
( 5 ) 3x – 5y = 30 માટે, જો x = 15 હોય, તો y શોધો.
૩. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) બે અંકની સંખ્યામાં એકમનો અંક x અને દશકનો અંક y હોય, તો તે સંખ્યા …….. છે.
A. x + y
B. yx
C. 10x + y
D. 10y + x
( 2 ) બિંદુ …….. એ 3x + y = 12ના આલેખ પરનું બિંદુ છે.
A. (1, 5)
B. (2, 10)
C. (4, 0)
D. (– 2, – 6)
( 3 ) સમીકરણ 5/x + 2/y = 6 માટે, જો x = 1 હોય, તો y = ………
A. 1/2
B. 2
C. 5
D. 1/5
( 4 ) બે સંખ્યાઓનો સરવાળો 16 અને તફાવત 4 હોય, તો તે પૈકીની મોટી સંખ્યા ……… છે.
A. 16
B. 20
C. 10
D. 6
( 5 ) 4x + 3y = 24નો આલેખ x-અક્ષને ……… બિંદુમાં છેદે.
A. (0, 8)
B. (0, − 8)
C. (6, 0)
D. (– 6, 0)
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) (6, 2 ) એ સમીકરણ 2x – 3y = 7નો એક ઉકેલ છે.
( 2 ) (7, 4) અને (– 3, 4)ને જોડતી રેખા પુ-અક્ષને (0, 4)માં છેદે.
( 3 ) સમીકરણ 5x + 0y – 13 = 0નો આલેખ x-અક્ષને સમાંતર રેખા છે.
( 4 ) જો (2, 3) એ સમીકરણ 5x + ky = 22નો એક ઉકેલ હોય, તો k = 4.
( 5 ) 2019x + 2020y = 0નો આલેખ ઉગમબિંદુમાંથી પસાર થતી રેખા છે.
જવાબો
1. (1) 4x – 3y – 24=0 (2) 24 (3) 59 (4) 5 (5) 0
2. ( 1 ) 5x – 3y – 60 = 0 (2) 16 (3) 4 ( 4 ) y = 3x–12/4 (5) 3
3. (1) 10y + x (2) (4, 0) (3) 2 (4) 10 (5) (6, 0)
4. ( 1 ) ખોટું ( 2 ) ખરું ( 3 ) ખોટું ( 4 ) ખરું ( 5 ) ખરું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here