Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 7 ત્રિકોણ
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 7 ત્રિકોણ
સ્વાધ્યાય – 7.1
1. ચતુષ્કોણ ACBDમાં AC = AD અને AB એ ∠Aનો દ્વિભાજક છે, (જુઓ આકૃતિ) સાબિત કરો કે Δ ABC = Δ ABD, BC અને BD વિશે તમે શું કહી શકો ?
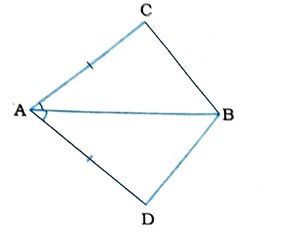
Δ ABC અને Δ ABDમાં
AC = AD (પક્ષ)
∠ BAC = ∠BAD (AB એ ∠Aનો દ્વિભાજક છે.)
AB = AB (સામાન્ય બાજુ)
∴ Δ ABC ≅ Δ ABD (બાખૂબા)
∴ BC = BD (CPCT)
આમ, BC અને BD સમાન છે.
2. જેમાં AD = BC અને ∠DAB = ∠CBA હોય તેવો ચતુષ્કોણ ABCD છે. (જુઓ આકૃતિ) સાબિત કરો કે,
(i) Δ ABD ≅ Δ BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC

Δ ABD અને Δ BACમાં
AD = BC (પક્ષ)
∠DAB = ∠CBA (પક્ષ)
AB = BA (સામાન્ય બાજુ)
∴ Δ ABD ≅ Δ BAC (બાખૂબા)
∴ BD = AC (CPCT)
∴ ∠ABD = ∠BAC (CPCT)
3. AD અને BC એ રેખાખંડ AB પરના સમાન લંબ છે. (જુઓ આકૃતિ) સાબિત કરો કે, CD એ ABને દુભાગે છે.

4. l અને m બે સમાંતર રેખાઓ છે. બીજી બે સમાંતર રેખાઓની જોડ p અને qની રેખાઓ તેમને છેદે છે. (જુઓ આકૃતિ)
સાબિત કરો કે, Δ ABC ≅ Δ CDA.

l || m અને AC તેમની છેદિકા છે.
∴ ∠BCA = ∠DAC (યુગ્મકોણ)
p || q અને AC તેમની છેદિકા છે.
∴ ∠BAC = ∠DCA (યુગ્મકોણ)
હવે, Δ ABC અને Δ CDAમાં
∠BCA = ∠DAC
∠BAC = ∠DCA
AC = AC (સામાન્ય બાજુ)
∴ Δ ABC ≅ Δ CDA (બાખૂબા)
5. કિરણ l એ ∠Aનો દ્વિભાજક છે અને B એ કિરણ l પરનું કોઈ બિંદુ છે. BP અને BQ એ Bમાંથી ∠Aની બાજુઓ પરના લંબ છે. (જુઓ આકૃતિ) સાબિત કરો કે,
(i) Δ APB ≅ Δ AQB
(ii) BP = BQ અથવા B એ ∠Aની બાજુઓથી સમાન અંતરે આવેલ છે.

l એ ∠PAQનો દ્વિભાજક છે અને B એ l પરનું બિંદુ છે.
∴ ∠PAB = ∠QAB
BP અને BQ એ Bમાંથી AP અને AQ પરના લંબ છે.
∴ ∠BPA = ∠BOA = 90°
હવે, Δ APB અને Δ AQBમાં
∠PAB = ∠QAB
∠BPA = ∠BQA
અને AB = AB (સામાન્ય બાજુ)
∴ Δ APB ≅ Δ AQB (ખૂખૂબા)
∴ BP = BQ (CPCT)
BP અને BQ એ ∠PQAના ભુજ AP અને AQ પરના લંબ છે.
∴ BPએ Bનું APથી અંતર છે અને BQ એ Bનું AQથી અંતર છે.
આમ, B એ ∠PAQની બાજુઓથી સમાન અંતરે છે.
6. આપેલ આકૃતિમાં AC = AE, AB = AD અને ∠BAD = ∠EAC. તો સાબિત કરો કે, BC = DE.
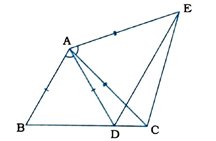
∠BAD = ∠EAC
∴ ∠BAD + ∠DAC = ∠EAC + ∠DAC
∴ ∠BAC = ∠DAE (આસન્નકોણ)
હવે, Δ BAC અને Δ DAEમાં,
AC = AE (પક્ષ)
AB = AD (પક્ષ)
∠BAC = ∠DAE
∴ Δ BAC ≅ Δ DAE (બાખૂબા)
∴ BC = DE (CPCT)
7. AB એક રેખાખંડ છે અને P તેનું મધ્યબિંદુ છે અને જેથી ∠BAD = ∠ABE અને ∠EPA = ∠DPB થાય તેવાં બિંદુઓ D તથા E રેખા ABની એક બાજુએ આવેલ છે. (જુઓ આકૃતિ) સાબિત કરો કે,

(i) Δ DAP ≅ Δ EBP
(ii) AD = BE
∠BAD = ∠ABE
∴ ∠PAD = ∠PBE ( ‘.’ P એ AB પરનું બિંદુ છે.)
∠EPA = ∠DPB
∴ ∠EPA + ∠EPD = ∠DPB + ∠EPD
∴ ∠APD = ∠BPE (આસન્નકોણ)
P એ ABનું મધ્યબિંદુ છે.
∴ AP = BP
હવે, Δ DAP અને Δ EBPમાં,
∠PAD = ∠PBE
∠APD = ∠BPE
AP = BP
∴ Δ DAP = Δ EBP (ખૂબાખૂ)
∴ AD = BE (CPCT)
8. કાટકોણ ત્રિકોણ ABCમાં ∠C કાટખૂણો છે. M એ કર્ણ ABનું મધ્યબિંદુ છે. DM = CM થાય તે રીતે Cને M સાથે જોડી D સુધી લંબાવો. બિંદુઓ D અને B જોડો. (જુઓ આકૃતિ)

સાબિત કરો કે,
(i) Δ AMC ≅ Δ BMD
(ii) ∠DBC કાટકોણ છે.
(iii) Δ DBC ≅ Δ ACB
(iv) CM = 1/2 AB
Δ AMC અને Δ BMDમાં
AM = BM (M એ ABનું મધ્યબિંદુ છે.)
CM = DM
∠AMC = ∠BMD (અભિકોણ)
∴ બાખૂબા મુજબ Δ AMC ≅ Δ BMD [પરિણામ (i)]
∴ ∠MCA = ∠MDB (CPCT)
∠MCA અને ∠MDB એ રેખાઓ AC અને BDની છેદિકા દ્વારા બનતા યુગ્મકોણ છે અને તેઓ સમાન છે.
∴ AC || BD
હવે, ∠DBC અને ∠ACB એ AC || BDની છેદિકા BC દ્વારા બનતા છેદિકાની એક તરફના અંતઃકોણ છે.
∴ ∠DBC + ∠ACB = 180°
∴ ∠DBC + 90° = 180° (પક્ષ : ∠C = 90°)
∴ ∠DBC = 90°
એટલે કે, ∠DBC કાટકોણ છે. [પરિણામ (ii)]
હવે, Δ AMC ≅ Δ BMD
∴ AC = BD
Δ DBC અને Δ ACBમાં
BD = CA
∠DBC = ∠ACB (કાટખૂણા)
BC = CB (સામાન્ય બાજુ)
∴ બાખૂબા મુજબ, Δ DBC ≅ Δ ACB [પરિણામ (iii)]
∴ DC = AB (CPCT)
DM = CM અને D રેખાખંડ CD પર આવેલું બિંદુ છે.
∴ DC = 2CM
∴ AB = 2CM
∴ 1/2 AB = CM
∴ CM = 1/2 AB [પરિણામ (iv)]
સ્વાધ્યાય – 7.2
1. જેમાં AB = AC હોય તેવા સમદ્વિબાજુ ત્રિકોણ ABCમાં ∠B અને ∠Cના દ્વિભાજકો એકબીજાને Oમાં છેદે છે. A અને Oને જોડો. સાબિત કરો કે,
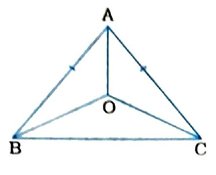
(i) OB = OC
(ii) AO એ ∠Aનો દ્વિભાજક છે.

2. Δ ABCમાં AD એ BCનો લંબદ્વિભાજક છે. (જુઓ આકૃતિ) સાબિત કરો કે, Δ ABC કે જેમાં AB = AC હોય તેવો સમદ્ધિબાજુ ત્રિકોણ છે.
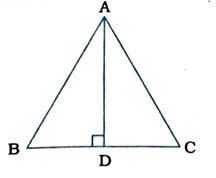
Δ ABCમાં AD એ BCનો લંબદ્વિભાજક છે.
∴ BD = CD અને ∠ADB = ∠ADC = 90°
Δ ADB અને Δ ADCમાં,
AD = AD (સામાન્ય બાજુ)
∠ADB = ∠ADC (કાટખૂણા)
અને BD = CD
∴ Δ ADB ≅ Δ ADC (બાખૂબા)
∴ AB = AC (CPCT)
હવે, Δ ABCમાં AB = AC
∴ Δ ABC સમતિબાજુ ત્રિકોણ છે, જેમાં AB = AC છે.
3. Δ ABC સમઢિબાજુ ત્રિકોણ છે. BE અને CF એ સમાન બાજુઓ અનુક્રમે AC અને AB પર વેધ છે. (જુઓ આકૃતિ) સાબિત કરો કે, આ વેધ સમાન છે.
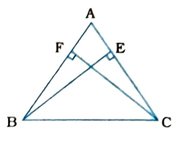
Δ ABCમાં AC = AB
∴ ∠ABC = ∠ACB
∴ ∠FBC = ∠ECB
હવે, Δ FBC અને Δ ECBમાં,
∠FBC = ∠ECB
∠BFC = ∠CEB (કાટખૂણા)
BC = CB (સામાન્ય બાજુ)
∴ ખૂખૂબા મુજબ, Δ FBC ≅ Δ ECB
∴ CF = BE (CPCT)
આમ, Δ ABCની સમાન બાજુઓ AC અને AB પરના વેધ BE અને CF સમાન છે.
4. Δ ABCની બાજુઓ AC અને AB પરના બે વેધ BE અને CF સમાન છે. (જુઓ આકૃતિ) સાબિત કરો કે,
(i) Δ ABE ≅ Δ ACF
(ii) AB = AC, અર્થાત્ ABC એ સમદ્વિબાજુ ત્રિકોણ છે.

Δ ABE અને Δ ACFમાં,
∠AEB = ∠AFC (કાટખૂણા)
∠A = ∠A (સામાન્ય ખૂણો)
BE = CF (પક્ષ)
∴ ખૂખૂબા મુજબ, Δ ABE = Δ ACF
∴ AB = AC (CPCT)
આમ, Δ ABC એ સમદ્વિબાજુ ત્રિકોણ છે.
5. ABC અને DBC એ સમાન પાયા BC પર આવેલા બે સમદ્વિબાજુ ત્રિકોણ છે. (જુઓ આકૃતિ) સાબિત કરો કે, ∠ABD = ∠ACD.



7. જેમાં ∠A = 90° અને AB = AC હોય તેવો કાટકોણ ત્રિકોણ ABC છે, તો ∠B અને ∠C શોધો.

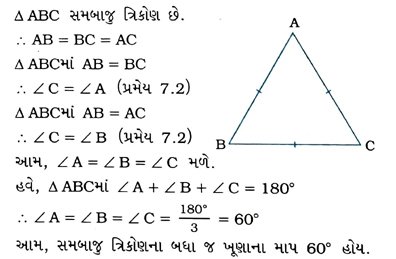
8. બતાવો કે સમબાજુ ત્રિકોણના બધા જ ખૂણાના માપ 60° હોય.
સ્વાધ્યાય – 7.3
1. Δ ABC અને Δ DBC સમાન પાયા BC પર આવેલા બે સમઢિબાજુ ત્રિકોણ છે અને શિરોબિંદુઓ A અને D એ BCની એક જ બાજુએ આવેલ છે (જુઓ આકૃતિ). જો ADને લંબાવતા તે BCને P બિંદુમાં છેદે તો સાબિત કરો કે,
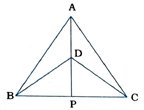
(i) Δ ABD ≅ Δ ACD
(ii) Δ ABP ≅ Δ ACP
(iii) AP એ ∠A તથા ∠Dને દુભાગે છે.
(iv) AP એ BCનો લંબદ્વિભાજક છે.

2. જેમાં AB = AC હોય તેવા Δ ABCનો વેધ AD છે, તો સાબિત કરો કે,
(i) AD એ BCને દુભાગે છે. (ii) AD એ ∠Aને દુભાગે છે.

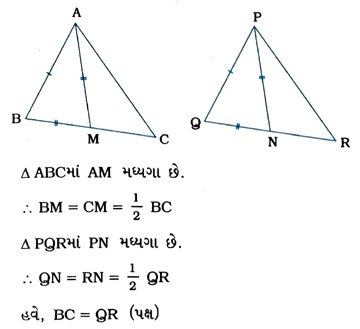
3. Δ ABCની બે બાજુઓ AB અને BC તથા મધ્યગા AM એ Δ PQRની અનુરૂપ બાજુઓ PQ અને QR તથા મધ્યગા PNને સમાન છે. (જુઓ આકૃતિ) તો સાબિત કરો કે,
(i) Δ ABM ≅ Δ PQN (ii) Δ ABC = Δ PQR

4. ત્રિકોણ ABCમાં BE અને CF બે સમાન વેધ છે, તો એકરૂપતા માટેની કાકબાની શરતનો ઉપયોગ કરી સાબિત કરો કે ABC સમઢિબાજુ ત્રિકોણ છે.
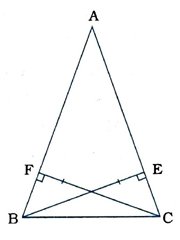
Δ FBC અને Δ ECBમાં
CF = BE (પક્ષ)
∠CFB = ∠BEC
= 90° (પક્ષ)
BC = CB (સામાન્ય બાજુ)
∴ કાકબા મુજબ Δ FBC ≅ Δ ECB
∴ ∠FBC = ∠ECB (CPCT)
∴ ∠ABC = ∠ACB
હવે, Δ ABCમાં ∠ABC = ∠ACB
∴ AC = AB (પ્રમેય 7.3)
આમ, Δ ABCમાં AB = AC હોવાથી Δ ABC સમદ્વિબાજુ ત્રિકોણ છે.
5. જેમાં AB = AC હોય તેવો સમઢિબાજુ ત્રિકોણ ABC છે. AP ⊥ BC દોરી ∠B = ∠C દર્શાવો.

Δ ABCમાં AP લંબ છે.
∴ ∠APB = ∠APC
= 90°
Δ APB અને Δ APCમાં,
∠APB = ∠APC = 90°
AB = AC (પક્ષ)
AP = AP (સામાન્ય બાજુ)
∴ કાકબા મુજબ, Δ APB ≅ Δ APC
∴ ∠ABP = ∠ACP (CPCT)
∴ ∠ABC = ∠ACB
આમ, Δ ABCમાં ∠B = ∠C થાય.
સ્વાધ્યાય – 7.4
1. સાબિત કરો કે, કર્ણ એ કાટકોણ ત્રિકોણની સૌથી મોટી બાજુ છે.
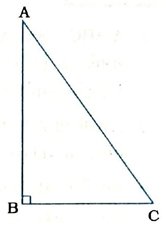
Δ ABCમાં ∠B કાટખૂણો છે.
∴ ∠B = 90° અને AC કર્ણ છે.
Δ ABCમાં,
∠A + ∠B + C = 180°
∴ ∠A + 90° + ∠C = 180°
∴ ∠A + ∠C = 90°
∠A અને ∠Cનું માપ હંમેશાં ધન સંખ્યા હોય અને તેઓનો સરવાળો 90° છે.
∴ ∠A < 90° અને ∠C < 90°
આથી ∠A < ∠Bઅને ∠C < ∠B
∴ BC < AC અને AB < AC (પ્રમેય 7.7)
આમ, કર્ણ AC એ બાકીની બંને બાજુ AB અને BCથી મોટી બાજુ છે.
આમ, કર્ણ એ કાટકોણ ત્રિકોણની સૌથી મોટી બાજુ છે.
2. આપેલ આકૃતિમાં Δ ABCની બાજુઓ AB અને ACને અનુક્રમે બિંદુ P તથા Q સુધી લંબાવેલ છે. વળી, ∠PBC < ∠QCB. સાબિત કરો કે, AC > AB.
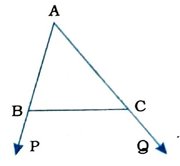
∠PBC < ∠QCB (પક્ષ)
∴ – ∠PBC > – ∠QCB (અસમતાને (– 1) વડે ગુણતાં અસમતા ફેરવાય)
∴ 180° – ∠PBC > 180° – ∠QCB (બંને બાજુ 180° ઉમેરતાં) …… (1)
હવે, ∠ABC અને ∠PBC રેખિક જોડ રચે છે તથા ∠ACB અને ∠QCB રેખિક જોડ રચે છે.
∴ ∠ABC = 180° – ∠PBC અને ∠ACB = 180° – ∠QCB
(1)માં ઉપરોક્ત કિંમતો મૂકતાં,
∠ABC > ∠ACB
Δ ABCમાં ∠ABC > ∠ACB
∴ AC > AB (પ્રમેય 7.7)
3. આપેલ આકૃતિમાં ∠B < ∠A અને ∠C < ∠D. તો સાબિત કરી કે, AD < BC.

Δ OABમાં ∠B < ∠A
∴ OA < OB (પ્રમેય 7,7) …… (1)
Δ OCDમાં ∠C < ∠D
∴ OD < OC (પ્રમેય 7,7) …… (2)
(1) અને (2)નો સરવાળો લેતા,
OA + OD < OB + OC
∴ AD < BC (O એ AD અને BCનું છેબિંદુ હોવાથી બંને રેખાખંડનુ બિંદુ છે.)
4. AB અને CD એ ચતુષ્કોણ ABCDની અનુક્રમે સૌથી નાની અને સૌથી મોટી બાજુઓ છે. (જુઓ આકૃતિ) સાબિત કરો કે, ∠A > ∠C અને ∠B > ∠D.
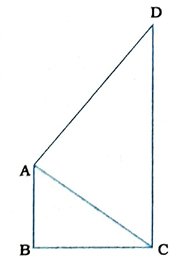
રચના : ચતુષ્કોણ ABCDનો વિકર્ણ AC રચો.
AB ચતુષ્કોણ ABCDની સૌથી નાની બાજુ અને CD ચતુષ્કોણ ABCDની સૌથી મોટી બાજુ છે.
∴ AB < BC અને AD < CD
Δ ABCમાં AB < BC
∴ ∠ACB < ∠BAC ……. (1)
Δ CDAમાં AD < CD
∴ ∠DCA < ∠DAC …….. (2)
(1) અને (2)નો સરવાળો લેતાં,
∠ACB + ∠DCA < ∠BAC + ∠DAC
∴ ∠BCD < ∠BAD
∴ ∠BAD > ∠BCD
આમ, ચતુષ્કોણ ABCDમાં ∠A > ∠C.
આ જ પ્રમાણૈ વિકર્ણ BDની રચના કરી Δ ABD અને Δ CBDની અસમતાનો ઉપયોગ કરીને ∠B > ∠D સાબિત થાય.
5. આપેલ આકૃતિમાં PR > PQ અને PS એ ∠QPRનો દ્વિભાજક હોય, તો સાબિત કરો કે ∠PSR > ∠PSQ.
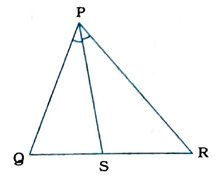
PS એ ∠QPRનો દ્વિભાજક છે.
∴ ∠QPS = ∠RPS = 1/2 ∠QPR …… (1)
∠PSR એ Δ PQSનો બહિષ્કોણ છે તથા ∠PSQ એ Δ PRSનો બહિષ્કોણ છે.
∴ ∠PSR = ∠Q + ∠QPS અને
∠PSQ = ∠R + ∠RPS …….. (2)
Δ PQRમાં PR > PQ
∴ ∠Q > ∠R
∴ ∠Q + 1/2 ∠QPR > ∠R + 1/2 ∠QPR
∴ ∠Q + ∠QPS > ∠R + ∠RPS [(1) પરથી]
∴ ∠PSR > ∠PSQ [(2) પરથી]
6. સાબિત કરો કે, રેખાની બહારના બિંદુમાંથી રેખા પર દોરેલ લંબ રેખાખંડ સૌથી નાનો રેખાખંડ હોય છે.

P એ રેખા ABની બહારનું બિંદુ છે.
રેખાખંડ PM એ Pમાં AB પર દોરેલ લંબ રેખાખંડ છે.
N એ રેખા AB પરનું Mથી ભિન્ન અન્ય કોઈ પણ બિંદુ છે.
Δ PMNમાં ∠M = 90°
∴ ∠N < 90°
આમ, Δ PMNમાં ∠N < ∠M
∴ PM < PN
આ હકીકત બિંદુ Nના કોઈ પણ સ્થાન માટે સત્ય છે.
∴ રેખાની બહારના બિંદુમાંથી રેખા પર દોરેલ લંબ રેખાખંડ સૌથી નાનો રેખાખંડ છે.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરો : (ફક્ત અંતિમ જવાબ)
( 1 ) APQRમાં જો ∠P = ∠Q હોય, તો ત્રિકોણની ……. બાજુઓ સમાન હોય.
( 2 ) ΔABCમાં ∠A = 60° અને ∠B = 70° હોય, તો ત્રિકોણની સૌથી મોટી બાજુ ……. થાય.
( 3 ) ΔXYZમાં XY = 5 સેમી, YZ = 7.2 સેમી અને ZX = 5.8 સેમી હોય, તો ત્રિકોણનો સૌથી મોટો ખૂણો ……. થાય.
( 4 ) સમાન પરિમિતિવાળા બે ……… ત્રિકોણ હંમેશાં એકરૂપ થાય.
( 5 ) જો APQR = A YXZ હોય, તો
∠PRQ = ∠ ……….
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) Δ ABC ≅ Δ RPQ છે. જો ∠A = 50° અને ∠B = 70° હોય, તો ∠Q શોધો.
( 2 ) ΔXYZમાં ∠Y =∠Z, XY = 6 સેમી અને YZ = 8 સેમી હોય, તો ΔXYZની પરિમિતિ શોધો.
( 3 ) Δ PQR સમદ્વિભુજ કાટકોણ ત્રિકોણ છે જેમાં PR કર્ણ છે. તો ∠P શોધો.
( 4 ) Δ PQRમાં PQ = 8 સેમી અને QR = 7 સેમી હોય, તો RPની લંબાઈ કેટલાં સેમીથી ઓછી જ હોય?
( 5 ) Δ ABC અને ΔXYZમાં AB = XZ, BC = ZY અને ∠B = ∠Z હોય, તો Δ ABC અને Δ XYZની એકરૂપતા સંકેતમાં દર્શાવો.
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) ΔABCમાં AB = BC અને ∠A = 40॰ હોય, તો ∠B = …….
A. 40°
B. 80°
C. 100°
D. 60°
( 2 ) જો બાજુઓના માપ (સેમીમાં) …….. હોય, તો તેવા ત્રિકોણની રચના કરવી શક્ય નથી.
A. 3, 4, 5
B. 5, 12, 13
C. 6, 8, 20
D. 6, 7, 10
( 3 ) Δ PQRમાં PQ = 9.2 સેમી અને PR = 7.6 સેમી હોય, તો QRની લંબાઈ ……… સૈમી ન હોઈ શકે,
A. 2.5
B. 3.5
C. 1.5
D. 4.5
( 4 ) Δ ABC અને Δ PORમાં AB = QR, BC = PQ અને AC = PR હોય, તો Δ ABC ≅ Δ ……..
A. PQR
B. RQP
C. PRQ
D. QPR
( 5 ) Δ ABCમાં AB = 8 સેમી, BC = 6 સેમી અને AC = 5 સેમી હોય, તો …….. સાચું છે.
A. ∠A > ∠C
B. ∠B > ∠A
C. ∠B < ∠C
D. ∠B > ∠C
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) સમદ્વિભુજ ત્રિકોણ ગુરુકોણ ત્રિકોણ હોઈ શકે.
( 2 ) A ABCમાં ∠A > ∠C > ∠B હોય, તો ત્રિકોણની સૌથી મોટી બાજુ AC છે.
( 3 ) Δ ABCમાં ∠A = 30° અને ∠B = 60॰ હોય, તો AC = 2BC થાય.
( 4 ) Δ ABCમાં ∠A = 40° અને ∠B = 50॰ હોય, તો ત્રિકોણની સૌથી મોટી બાજુ AB છે.
( 5 ) જેની બાજુઓના માપ 5 સેમી, 8 સેમી અને 15 સેમી હોય તેવા ત્રિકોણની રચના શક્ય છે.
જવાબો
1. ( 1 ) PR અને QR (2) AC (3) ∠X ( 4 ) સમબાજુ ( 5 ) YZX
2. ( 1 ) 60° ( 2 ) 20 સેમી ( 3 ) 45° ( 4 ) 15 સેમીથી ( 5 ) ΔABC ≅ Δ XZY
3. ( 1 ) 100° ( 2 ) 6, 8, 20 ( 3 ) 1.5 ( 4 ) RQP ( 5 ) ∠B < ∠C
4. ( 1 ) ખરું ( 2 ) ખોટું ( 3 ) ખોટું ( 4 ) ખરું ( 5 ) ખોટું
સ્વાધ્યાય – 7.5 (વૈકલ્પિક)*
1. ABC ત્રિકોણ છે. જે Δ ABCનાં ત્રણેય શિરોબિંદુઓથી સમાન અંતરે આવેલ હોય એવું બિંદુ Δ ABCના અંદરના ભાગમાં મેળવો.
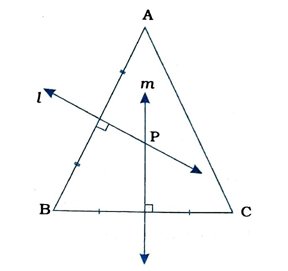
Δ ABCની બાજુ ABનો લંબદ્વિભાજક l તથા બાજુ BCનો લંબદ્વિભાજક m રચો. l અને mના છેદબિંદુને P નામ આપો. P એ ABના લંબદ્વિભાજક પરનું બિંદુ છે. માટે P એ A અને Bથી સમાન અંતરે છે.
∴ PA = PB
P એ BCના લંબદ્વિભાજક પરનું બિંદુ છે.
∴ PB = PC
આમ, PA = PB = PC
આમ, P એ Δ ABCનાં ત્રણેય શિરોબિંદુઓથી સમાન અંતરે આવેલું બિંદુ છે.
આ બિંદુ Pને Δ ABCનું પરિકેન્દ્ર કહે છે.
નોંધ : અહીં, Δ ABC લઘુકોણ ત્રિકોણ હોવાથી બિંદુ P Δ ABCના અંદરના ભાગમાં મળે. જો Δ ABC કાટકોણ ત્રિકોણ હોય, તો બિંદુ P એ કર્ણ પર મળે (કર્ણનું મધ્યબિંદુ) અને જો Δ ABC ગુરુકોણ ત્રિકોણ હોય, તો બિંદુ P ત્રિકોણની બહારના ભાગમાં મળે.
2. જે ત્રિકોણની ત્રણેય બાજુઓથી સમાન અંતરે આવેલું હોય એવું બિંદુ ત્રિકોણના અંદરના ભાગમાં મેળવો.
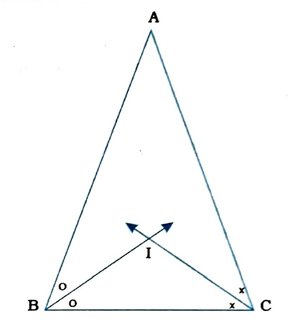
Δ ABCના ખૂણા ∠B અને ∠Cના દ્વિભાજકો રચો અને તેમના છેદબિંદુને I નામ આપો.
I એ ∠Bના દ્વિભાજક પરનું બિંદુ છે. માટે I એ બાજુઓ BA અને BCથી સમાન અંતરે છે. તે જ રીતે I એ ∠Cના દ્વિભાજક પરનું બિંદુ છે. માટે I એ બાજુઓ CB અને CAથી સમાન અંતરે છે.
આમ, I એ Δ ABCની ત્રણેય બાજુઓ AB, BC અને ACથી સમાન અંતરે આવેલ બિંદુ છે.
આ બિંદુ Iને Δ ABCનું અંત:કેન્દ્ર કહે છે.
3. એક વિશાળ બગીચામાં લોકો ત્રણ સ્થળે એકઠા થયેલ છે. (જુઓ આકૃતિ)
A: આ સ્થાન પર બાળકો માટેના જુદા જુદા હીંચકા અને લપસણી છે.
B: આ સ્થાનની નજીક માનવ-નિર્મિત તળાવ આવેલું છે.
C : આ સ્થાનની નજીક પર વિશાળ પાર્કિંગ તથા બહાર નીકળવાનો માર્ગ આવેલ છે.
કયાં સ્થળે આઇસક્રીમ પાર્લર ઊભું કરવું જોઈએ કે જેથી વધુમાં વધુ લોકો આવી શકે?
(સૂચના A, B અને Cથી સમાન અંતરે પાર્લર આવેલું હોવું જોઈએ.)
સૌપ્રથમ સ્થાન (હિંદુ) A, B અને C દ્વારા બનતો Δ ABC રચો. ત્યારબાદ દાખલા નં. 1માં બતાવ્યું તે પ્રમાણે કોઈ પણ બે બાજુઓના લંબદ્વિભાજકનું છેદબિંદુ P મેળવો. આ બિંદુ Pનું સ્થાન આઇસક્રીમ પાર્લર ઊભું કરવા માટેનું ઉત્તમ સ્થળ થાય કા૨ણ કે તે ત્રણેય સ્થળ A, B અને Cથી સમાન અંતરે છે.
4. આપેલ આકૃતિ (1) અને (2)માં દર્શાવેલ ષટ્કોણીય અને તારા આકારની રંગોળીને વધુમાં વધુ 1 સેમી બાજુવાળા સમબાજુ ત્રિકોણ જેટલા સમાય તેટલા ભરો. બંને કિસ્સામાં આવાં ત્રિકોણોની સંખ્યા ગણો. કઈ આકૃતિમાં વધુ ત્રિકોણ હશે?
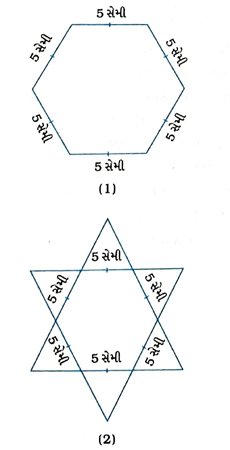
આકૃતિ (1)ની ષટ્કોણીય રંગોળીના વિકર્ણોના છેદબિંદુ દ્વારા બિંદુ O મળે. બિંદુ Oને ષટ્કોણ ABCDEFનાં શિરોબિંદુઓ સાથે ક્રમિક રીતે જોડવાથી છ સમબાજુ ત્રિકોણ બને જે દરેકમાં બાજુની લંબાઈ 5 સેમી હોય. આવા એક ત્રિકોણમાં નીચેની આકૃતિમાં દર્શાવેલ છે તે રીતે 1 સેમી લંબાઈવાળા 25 ( 1 + 3 + 5 + 7 + 9) સમબાજુ ત્રિકોણ સમાય. આથી ષટ્કોણીય રંગોળી ABCDEFમાં 25 × 6 = 150 ત્રિકોણ સમાય.
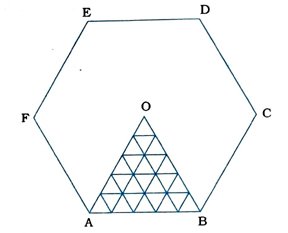
તે જ રીતે આકૃતિ 2માં અંદરના ષટ્કોણીય ભાગમાં 150 ત્રિકોણ અને બહારના 6 ત્રિકોણમાં 25 × 6 = 150 ત્રિકોણ સમાય. આમ. આકૃતિ (2)માં 150 + 150 = 300 ત્રિકોણ સમાય.
આકૃતિ (2)માં વધુ ત્રિકોણ સમાય.
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here