Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 8 ચતુષ્કોણ
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 8 ચતુષ્કોણ
સ્વાધ્યાય – 8.1
1. એક ચતુષ્કોણના ખૂણાઓનો ગુણોત્તર 3: 5: 9 : 13 છે. આ ચતુષ્કોણના બધા જ ખૂણાઓ શોધો.
ધારો કે, ચતુષ્કોણ ABCD એ આપેલ ચતુષ્કોણ છે.
∴ ∠A : ∠B : ∠C : ∠D = 3 : 5 : 9 : 13
ગુણોત્તરોનો સરવાળો = 3 + 5 + 9 + 13 = 30
ચતુષ્કોણ ABCDમાં ∠A + ∠B + ∠C + ∠D = 360°
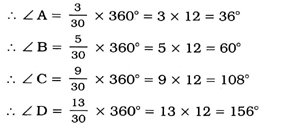
આમ, આપેલ ચતુષ્કોણના ખૂણાઓ અનુક્રમે 36°, 60°, 108 અને 156° છે.
2. જો સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો સમાન હોય, તો દર્શાવો કે તે લંબચોરસ છે.
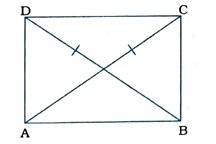
સમાંતરબાજુ ચતુષ્કોણ ABCDમાં વિકર્ણો સમાન છે, એટલે કે AC = BD.
Δ DAB અને Δ CBAમાં,
DA = CB (પ્રમેય 8.2)
AB = BA (સામાન્ય બાજુ)
DB = CA (પક્ષ)
∴ બાબાબા મુજબ, Δ DAB ≅ Δ CBA
∴ ∠DAB = ∠CBA (CPCT)
સમાંતરબાજુ ચતુષ્કોણ ABCDમાં AD || BC અને AB તેમની છેદિકા છે.
∴ ∠DAB + ∠CBA = 180° (છેદિકાની એક તરફના અંતઃકોણ)
આમ, ∠DAB અને ∠CBA પૂરકકોણ છે અને તેઓ સમાન છે.
∴ ∠DAB = ∠CBA = 90°
એટલે કે, સમાંતરબાજુ ચતુષ્કોણ ABCDમાં ∠A અને ∠B બંને કાટખૂણા છે. માટે, સમાન વિકર્ણો ધરાવતો સમાંતરબાજુ ચતુષ્કોણ ABCD લંબચોરસ છે.
3. સાબિત કરો કે, જો ચતુષ્કોણના વિકર્ણો એક્બીજાને કાટખૂણે દુભાગે, તો તે સમબાજુ ચતુષ્કોણ છે.
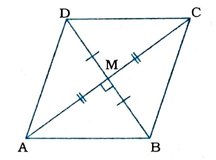
ચતુષ્કોણ ABCDના વિકર્ણો AC અને BD M બિંદુમાં કાટખૂણે દુભાગે છે.
∴ AM = CM, BM = DM અને
∠AMB = ∠CMB = ∠CMD = ∠AMD = 90°
Δ AMB અને Δ CMBમાં,
AM = CM
∠AMB = ∠CMB
BM = BM (સામાન્ય બાજુ)
∴ બાખુબા મુજબ, Δ AMB ≅ Δ CMB
∴ AB = CB (CPCT)
તે જ રીતે Δ BMC ≅ Δ DMC અને Δ DMA ≅ Δ BMA સાબિત કરવાથી BC = DC અને DA = BA મળે.
આમ, ચતુષ્કોણ ABCDમાં AB = BC = CD = DA. આથી ચતુષ્કોણ ABCD સમબાજુ ચતુષ્કોણ છે.
આમ, જો ચતુષ્કોણના વિકર્ણો એકબીજાને કાટખૂણે દુભાગે, તો તે સમબાજુ ચતુષ્કોણ છે.
4. સાબિત કરો કે, ચોરસના વિર્ણો સમાન છે અને તે એકબીજાને કાટખૂણે દુભાગે છે.

ABCD એ આપેલ ચોરસ છે, જેના વિકર્ણી AC અને BD એકબીજાને Mમાં છેદે છે.
પ્રત્યેક ચોરસ એ સમાંતરબાજુ ચતુષ્કોણ પણ છે જ.
∴ AC અને BD એકબીજાને દુભાગે છે. …… (1)
Δ DAB અને Δ CBAમાં,
DA = CB (ચોરસની બાજુઓ)
∠DAB = ∠CBA (ચોરસના ખૂણા કાટખૂણા)
AB = BA (સામાન્ય બાજુ)
∴ બાખૂબા મુજબ Δ DAB ≅ Δ CBA
∴ BD = AC (CPCT) …….. (2)
હવે, Δ AMB અને Δ CMBમાં,
AM = CM (BD એ ACને Mમાં દુભાગે છે)
BM = BM (સામાન્ય બાજુ)
AB = CB (ચોરસની બાજુઓ)
∴ બાબાબા મુજબ, Δ AMB ≅ Δ CMB
∴ ∠AMB = ∠CMB (CPCT)
પરંતુ, ∠AMB અને ∠CMB રેખિક જોડના ખૂણા છે
∴ ∠AMB + ∠CMB = 180°
આમ, ∠AMB = ∠CMB = 90° ……. (3)
(1), (2) અને (3) પરથી સાબિત થાય છે કે ચોરસના વિકર્ણો સમાન છે અને તે એક્બીજાને કાટખૂણે દુભાગે છે.
5. સાબિત કરો કે, જો ચતુષ્કોણના વિકર્ણો સમાન હોય તથા તે એકબીજાને કાટખૂણે દુભાગે, તો તે ચોરસ છે.
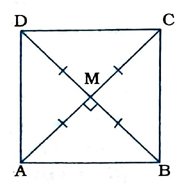
ચતુષ્કોણ ABCDના વિર્ણો AC અને BD સમાન છે તથા એક્બીજાને M બિંદુમાં કાટખૂણે દુભાગે છે.
∴ AC = BD.
MA = MC = MB = MD = 1/2 AC = 1/2 BD તથા
∠AMB = ∠CMB = ∠DMC = ∠DMA = 90°
Δ AMB અને Δ CMBમાં,
AM = CM
∠AMB = ∠CMB (કાટખૂણા)
BM = BM (સામાન્ય બાજુ)
∴ બાખૂબા મુજબ Δ AMB ≅ Δ CMB
∴ AB = CB (CPCT)
તે જ રીતે BC = DC અને DA = BA મળે,
આમ, ચતુષ્કોણ ABCDમાં,
AB = BC = CD = DA મળે. ……. (1)
Δ DAB અને Δ CBAમાં,
DA = CB
BD = AC (પક્ષ)
AB = BA (સામાન્ય બાજુ)
∴ બાબાબા મુજબ, Δ DAB ≅ Δ CBA
∴ ∠DAB = ∠CBA (CPCT)
આમ, ચતુષ્કોણ ABCDમાં ∠A = ∠B મળે,
તે જ રીતે ∠B = ∠C અને ∠C = ∠D મળે,
આમ, ચતુષ્કોણ ABCDમાં ∠A = ∠B = ∠C = ∠D વળી, ચતુષ્કોણ ABCDમાં,
∠A + ∠B + ∠C + ∠D = 360°
∴ ∠A = ∠B = ∠C = ∠D = 360°/4 = 90° … … (2)
આથી (1) અને (2) પરથી સાબિત થાય છે કે ચતુષ્કોણની ચારેય બાજુઓ સમાન છે તથા ચારેય ખુણા સમાન છે.
આથી ચતુષ્કોણ ABCD ચોરસ છે.
આમ, જો ચતુષ્કોણના વિકર્ણો સમાન હોય તથા તે એક્બીજાને કાટખૂણે દુભાગે, તો તે ચોરસ છે.
6. સમાંતરબાજુ ચતુષ્કોણ ABCDનો વિકર્ણ AC એ ∠Aને દુભાગે છે. (જુઓ આકૃતિ) સાબિત કરો કે, (I) તે ∠Cને પણ દુભાગે છે. (ii) ABCD સમબાજુ ચતુષ્કોણ છે.

સમાંતરબાજુ ચતુષ્કોણ ABCDનો વિર્ણ AC એ ∠Aને દુભાગે છે.
∴ ∠DAC = ∠BAC …… (1)
હવે, ∠BAC અને ∠DCA એ AB || CDની છેદિકા AC દ્વારા બનતા યુગ્મકોણ છે.
∴ ∠BAC = ∠DCA …….. (2)
તે જ રીતે, ∠ DAC અને ∠ BCA એ AD || BCની છેદિકા AC દ્વારા બનતા યુગ્મકોણ છે.
∴ ∠ DAC = ∠ BCA ……. (3)
(1), (2) અને (3) પરથી,
∠ DCA = ∠ BCA
વળી, ∠ DCA + ∠ BCA = ∠ BCD (આસન્નકોણ)
આથી AC એ ∠Cને પણ દુભાગે છે. …પરિણામ (i)
સમાંતરબાજુ ચતુષ્કોણ ABCDમાં,
∠A = ∠C (પ્રમેય 8.4)

∴ Δ DACમાં DA = DC (સમાન ખૂણાની સામેની બાજુઓ)
વળી, સમાંતરબાજુ ચતુષ્કોણ ABCDમાં,
AB = CD અને BC = DA (પ્રમેય 8.2)
∴ AB = BC = CD = DA
આમ, ચતુષ્કોણ ABCDમાં ચારેય બાજુઓ સમાન છે.
માટે, ABCD સમબાજુ ચતુષ્કોણ છે. … પરિણામ (ii)
7. ABCD સમબાજુ ચતુષ્કોણ છે. સાબિત કરો કે, વિકર્ણ AC એ ∠A તેમજ ∠Cને દુભાગે છે તથા વિકર્ણ BD એ ∠B તેમજ ∠Dને દુભાગે છે.
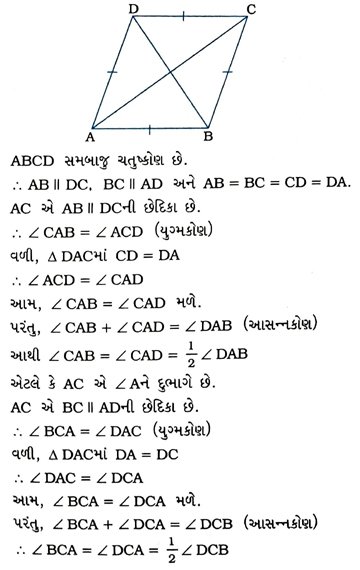
એટલે કે, AC એ ∠Cને દુભાગે છે.
આમ, AC એ ∠A તેમજ ∠Cને દુભાગે છે.
આ જ રીતે વિકર્ણ BD લેતાં સાબિત કરી શકાય કે, BD એ ∠B તેમજ ∠Dને દુભાગે છે.
8. લંબચોરસ ABCDમાં વિકર્ણ AC એ ∠A તેમજ ∠Cને દુભાગે છે. સાબિત કરો કે, (i) ABCD ચોરસ છે. (ii) વિકર્ણ BD એ ∠B તેમજ ∠Dને દુભાગે છે.

9. સમાંતરબાજુ ચતુષ્કોણ ABCDમાં વિકર્ણ BD પર બે બિંદુઓ P અને Q એવાં લીધાં છે કે જેથી DP = BQ થાય. (જુઓ આકૃતિ) બતાવો કે, (i) Δ APD ≅ Δ CQB (ii) AP = CQ (iii) Δ AQB ≅ Δ CPD (iv) AQ = CP (v) APCQ સમાંતરબાજુ ચતુષ્કોણ છે.
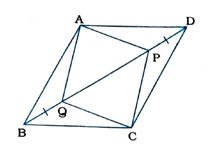
ABCD સમાંતરબાજુ ચતુષ્કોણ છે.
∴ AD || BC અને વિકર્ણ BD તેમની છેદિકા છે.
∴ ∠ADB = ∠CBD (યુગ્મકોણ)
∴ ∠ADP = ∠CBQ …… (1)
તે જ રીતે, CD || BA અને BD તેમની છેદિકા છે.
∴ ∠ABD = ∠CDB (યુગ્મકોણ)
∴ ∠ABQ = ∠CDP ……. (2)
Δ APD અને Δ CQBમાં,
AD = CB (સમાંતરબાજુ ચતુષ્કોણની સામસામેની બાજુ)
∠ADP = ∠CBQ [(1) મુજબ]
DP = BQ (પક્ષ)
∴ બાખૂબા મુજબ Δ APD ≅ Δ CQB …. પરિણામ (i)
∴ AP = CQ (CPCT) …. પરિણામ (ii)
Δ AQB અને Δ CPDમાં,
AB = CD (સમાંતરબાજુ ચતુષ્કોણની સામસામેની બાજુ)
∠ABG = ∠CDP [(2) મુજબ]
BQ = DP (પક્ષ)
∴ બાખૂબા મુજબ, Δ AQB ≅ Δ CPD …. પરિણામ (iii)
∴ AQ = CP (CPCT) …. પરિણામ (iv)
હવે, ચતુષ્કોણ APCOમાં AP = CQ અને AQ = CP હોવાથી પ્રમેય 8.3 મુજબ APCQ સમાંતરબાજુ ચતુષ્કોણ છે. …. પરિણામ (v)
10. ABCD સમાંતરબાજુ ચતુષ્કોણ છે અને શિરોબિંદુઓ A અને Cમાંથી વિકર્ણ BD પર અનુક્રમે AP અને CQ લંબ દોરેલ છે. (જુઓ આકૃતિ) સાબિત કરો કે, (i) Δ APB ≅ Δ CQD (ii) AP = CQ

સમાંતરબાજુ ચતુષ્કોણ ABCDમાં AB || CD અને BD તેમની છેદિકા છે.
∴ ∠ABD = ∠CDB (યુગ્મકોણ)
∴ ∠ABP = ∠CDQ
હવે, Δ APB અને Δ CODમાં,
AB = CD (સમાંતરબાજુ ચતુષ્કોણની સામસામેની બાજુ)
∠ABP = ∠CDQ [(1) મુજબ] (1)
∠APB = ∠CQD (કાટખૂણા)
∴ ખૂખૂબા મુજબ, Δ APB = Δ CQD … પરિણામ ( i )
∴ AP = CQ (CPCT) … પરિણામ (ii)
11. Δ ABC અને Δ DEFમાં AB = DE, AB || DE, BC = EF અને BC | EF છે. શિરોબિંદુઓ A, B અને C અનુક્રમે D, E અને F સાથે જોડાયેલાં છે. (જુઓ આકૃતિ) સાબિત કરો કે,
(i) ચતુષ્કોણ ABED એ સમાંતરબાજુ ચતુષ્કોણ છે.
(ii) ચતુષ્કોણ BEFC એ સમાંતરબાજુ ચતુષ્કોણ છે.
(iii) AD || CF AD = CF
(iv) ચતુષ્કોણ ACFD એ સમાંતરબાજુ ચતુષ્કોણ છે.
(v ) AC = DF
(vi) Δ ABC ≅ Δ DEF

ચતુષ્કોણ ABEDમાં AB = DE અને AB || DE, એટલે કે ચતુષ્કોણ ABEDની સામસામેની બાજુઓની એક જોડ સમાન અને સમાંતર છે.
∴ પ્રમેય 8.8 મુજબ ચતુષ્કોણ ABED એ સમાંતરબાજુ ચતુષ્કોણ છે. …. પરિણામ (i)
તે જ રીતે, ચતુષ્કોણ BEFCમાંBC = EF અને BC || EF હોવાથી પ્રમેય 8.8 મુજબ ચતુષ્કોણ BEFC એ સમાંતરબાજુ ચતુષ્કોણ છે. … પરિણામ (ii)
સમાંતરબાજુ ચતુષ્કોણ ABEDમાં AD || BE અને સમાંતરબાજુ ચતુષ્કોણ BEFCમાં BE || CF. આમ, AD અને CF બંને એક જ રેખાખંડ BEને સમાંતર છે.
∴ AD || CF …. (1)
સમાંતરબાજુ ચતુષ્કોણ ABEDમાં AD = BE અને સમાંતરબાજુ ચતુષ્કોણ BEFCમાં BE = CF
∴ AD = CF …. (2)
(1) અને (2)ને સાથે લેતાં,
AD || CF AD = CF ….. પરિણામ (iii)
ચતુષ્કોણ ACFDમાં AD || CF અને AD = CF
∴ પ્રમેય 8.8 મુજબ ચતુષ્કોણ ACFD એ સમાંતરબાજુ ચતુષ્કોણ છે. …. પરિણામ (iv)
AC અને DF એ સમાંતરબાજુ ચતુષ્કોણ ACFDની સામસામેની બાજુઓ છે.
∴ AC = DF …… પરિણામ (v)
Δ ABC અને Δ DEFમાં,
AB = DE (પક્ષ)
BC = EF (પક્ષ)
AC = DF [પરિણામ (v) મુજબ]
∴ બાબાબા મુજબ, Δ ABC ≅ Δ DEF … પરિણામ (vi)
12. સમલંબ ચતુષ્કોણ ABCDમાં AB || CD અને AD = BC. (જુઓ આકૃતિ) સાબિત કરો કે,
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) Δ ABC ≅ Δ BAD
(iv) વિકર્ણ AC = વિકર્ણ BD
[ સૂચના : AB ને લંબાવો અને Cમાંથી DAને સમાંતર તથા ABને Eમાં છેદતી એક રેખા દોરો.]
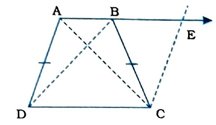
ABને E સુધી લંબાવેલ છે અને AB || CD.
∴ AE || CD
ચતુષ્કોણ ADCEમાં AE | CD અને રચના મુજબ CE || DA.
∴ ચતુષ્કોણ ADCE એ સમાંતરબાજુ ચતુષ્કોણ છે.
માટે, AD = CE અને AD = BC (પક્ષ)
∴ BC = CE
Δ BCEમાં BC = CE હોવાથી,
∠CBE = ∠CEB
∴ ∠CBE = ∠CEA …. (1)
સમાંતરબાજુ ચતુષ્કોણ ADCEમાં AD || CE અને AE તેમની છેદિકા છે.
∴ ∠DAE + ∠CEA = 180° (છેદિકાની એક તરફના અંતઃકોણ)
∴ ∠DAE + ∠CBE = 180° [(1) પરથી]
∴ ∠DAE = 180°− ∠CBE ….. (2)
વળી, ∠ABC + ∠CBE = 180° (ખિક જોડ)
∴ ∠ABC = 180° – ∠CBE …. (3)
(2) અને (3) પરથી,
∠DAE = ∠ABC
∴ ∠A = ∠B ….. પરિણામ (1)
AB || CD અને AD તેમની છેદિકા છે.
∴ ∠A + ∠D = 180°
∴ ∠D = 180° – ∠A ….. (4)
AB || CD અને BC તેમની છેદિકા છે.
∴ ∠B + ∠C = 180°
∴ ∠C = 180° – ∠B
∴ ∠C = 180° – ∠A [પરિણામ (i) મુજબ] … (5)
(4) અને (5) પરથી
∠C = ∠D … પરિણામ (ii)
વિકર્ણો AC અને BD દોરો.
Δ ABC અને Δ BADમાં,
BC = AD (પક્ષ)
∠ABC = ∠BAD (પરિણામ (i) મુજબ)
AB = BA (સામાન્ય બાજુ)
∴ બાખૂબા મુજબ, Δ ABC ≅ Δ BAD …. પરિણામ (iii)
∴ AC = BD (CPCT)
આમ, વિકર્ણ AC = વિકર્ણ_BD ….. પરિણામ (iv)
નોંધ : જે સમલંબ ચતુષ્કોણમાં બિનસમાંતર બાજુઓની જોડ સમાન હોય તે સમલંબ ચતુષ્કોણને સમદ્વિબાજુ સમલંબ ચતુષ્કોણ કહે છે. ઉપ૨ સાબિત કર્યા મુજબ તેના વિર્ણો સમાન હોય તથા સમાંતરબાજુઓ પરના ખૂણા સમાન હોય.
સ્વાધ્યાય – 8.2
1. ચતુષ્કોણ ABCDની બાજુઓ AB, BC, CD અને DAનાં મધ્યબિંદુઓ અનુક્રમે P, Q, R અને S છે. (જુઓ આકૃતિ 1) AC તેનો વિકર્ણ છે. સાબિત કરો કે,
(i) SR || AC અને SR = 1/2 AC
(ii) PQ = SR
(lil) PQRS સમાંતરબાજુ ચતુષ્કોણ છે.


2. ABCD સમબાજુ ચતુષ્કોણ છે અને P, Q, R અને s એ અનુક્રમે બાજુઓ AB, BC, CD અને DAનાં મધ્યબિંદુઓ છે. સાબિત કરો કે ચતુષ્કોણ PQRS એ લંબચોરસ છે.

∴ ∠DNP + ∠NPS = 180°
∴ ∠MNP + ∠NPS = 180°
∴ 90° + ∠NPS = 180°
∴ ∠NPS = 90º
∴ ∠SPQ = 90°
આમ, સમાંતરબાજુ ચતુષ્કોણ PQRSનો એક ખૂશી ∠P કાટખૂણો છે.
∴ ચતુષ્કોણ PQRS લંબચોરસ છે.
3. ABCD લંબચોરસ છે અને તેની બાજુઓ AB, BC, CD અને DAનાં મધ્યબિંદુઓ અનુક્રમે P, Q, R અને s છે. સાબિત કરો કે ચતુષ્કોણ PQRS એ સમબાજુ ચતુષ્કોણ છે.

4. સમલંબ ચતુષ્કોણ ABCDમાં AB || DC, BD વિકર્ણ છે અને ADનું મધ્યબિંદુ E છે. Eમાંથી ABને સમાંતર અને BCને Fમાં છેદતી એક રેખા દોરી છે. (જુઓ આકૃતિ) Fએ BCનું મધ્યબિંદુ છે તેમ બતાવો.
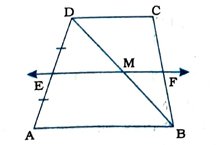
ધારો કે, દમાંથી ABને સમાંતર દોરેલ રેખાEF એ BDને Mમાં છેદે છે.
EF || AB અને AB || DC
∴ EF || DC
વિકર્ણ BD દ્વારા બે ત્રિકોણ Δ ABD અને Δ BCD મળે છે. Δ ABDમાં E એ ADનું મધ્યબિંદુ અને Eમાંથી ABને સમાંતર દોરેલ રેખા BDને Mમાં છંદ છે.
માટે, પ્રમેય 8,10 મુજબ M એ BDનું મધ્યબિંદુ છે.
હવે, Δ BCDમાં M એ BDનું મધ્યબિંદુ છે અને Mમાંથી પસાર થતી રેખા MF એ DCને સમાંતર છે.
માટે, પ્રમેય 8,10 મુજબ Fએ BCનું મધ્યબિંદુ છે.
નોંધ : અહીં EFની લંબાઈ અંગેનું નીચે મુજબનું પરિણામ પણ મેળવી શકાય :

5. સમાંતરબાજુ ચતુષ્કોણ ABCDમાં બાજુઓ AB અને CDનાં મધ્યબિંદુઓ અનુક્રમે E અને F છે. (જુઓ આકૃતિ) સાબિત કરો કે, રેખાખંડ AF અને EC વિકર્ણ BDનું ત્રણ સમાન ભાગમાં વિભાજન કરે છે.

(1) અને (2) પરથી DP = PQ = QB અને
DP + PQ + QB = BD.
આમ, AF અને EC એ વિકર્ણ BDનું ત્રણ સમાન ભાગમાં વિભાજન કરે છે.
6. સાબિત કરો કે, ચતુષ્કોણની સામસામેની બાજુઓનાં મધ્યબિંદુઓને જોડતાં રેખાખંડ એકબીજાને દુભાગે છે.

ચતુષ્કોણ ABCDની બાજુઓ AB, BC, CD અને DAનાં મધ્યબિંદુઓ અનુક્રમે P, Q, R અને S છે.
Δ ABCમાં P અને Q અનુક્રમે AB અને BCનાં મધ્યબિંદુઓ છે.
Δ ADCમાં S અને R અનુક્રમે DA અને DCનાં મધ્યબિંદુઓ છે.
(1) અને (2) પરથી,
PQ = SR અને PQ || SR મળે.
આમ, ચતુષ્કોણ PQRSની સામસામેની બાજુઓની એક જોડ સમાન અને સમાંતર છે.
આથી ચતુષ્કોણ PQRS સમાંતરબાજુ ચતુષ્કોણ છે.
સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો પરસ્પર દુભાગે છે. [પ્રમેય 8.6] આથી PR અને SQ એક્બીજાને દુભાગે છે.
આમ, ચતુષ્કોણની સામસામેની બાજુઓનાં મધ્યબિંદુઓને જોડતાં રેખાખંડ એક્બીજાને દુભાગે છે.
7. Δ ABCમાં ∠C કાટકોણ છે. કર્ણ ABના મધ્યબિંદુ Mમાંથી પસાર થતી અને BCને સમાંતર રેખા ACને Dમાં છેદે છે. સાબિત કરો કે,
(i) D એ ACનું મધ્યબિંદુ છે.
(ii) MD ⊥ AC
(iii) CM = MA = 1/2 AB
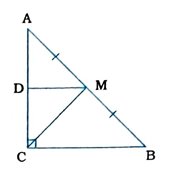
Δ ABCમાં ∠C કાટકોણ છે. કર્ણ ABના મધ્યબિંદુ Mમાંથી પસાર થતી અને BCને સમાંતર રેખા ACને Dમાં છેદે છે.
આથી પ્રમેય 8.10 મુજબ DM એ ACને દુભાગે છે.
માટે, D એ ACનું મધ્યબિંદુ છે. ….. પરિણામ (i)
Δ ABCમાં ∠C કાટખૂણો છે.
∴ ∠C = 90°
BC || DM અને DC તેમની છેદિકા છે.
∴ ∠MDC + ∠DCB = 180° (છેદિકાની એક તરફના અંતઃકોણ)
∴ ∠MDC + 90° = 180°
∴ ∠MDC = 90°
આમ, MD એ ACને લંબ છે.
એટલે કે, MD ⊥ AC ….. પરિણામ (ii)
હવે, Δ ADM અને Δ CDMમાં,
AD = CD (D એ ACનું મધ્યબિંદુ છે.)
∠ADM = ∠CDM (MD ⊥ AC હોવાથી કાટખૂણા)
DM = DM (સામાન્ય બાજુ)
∴ બાખૂબા મુજબ, Δ ADM ≅ Δ CDM
∴ AM = CM (CPCT) … (1)
વળી M એ ABનું મધ્યબિંદુ છે.
∴ AM = 1/2 AB … (2)
(1) અને (2) પરથી,
CM = MA = 1/2 AB સાબિત થાય. …… પરિણામ (iii)
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરોઃ (ફક્ત અંતિમ જવાબ)
( 1 ) સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો પરસ્પર ………. છે.
( 2 ) ચતુષ્કોણના ચારેય ખૂણાઓનો સરવાળો ……… થાય.
( 3 ) સમાંતરબાજુ ચતુષ્કોણનો કોઈ પણ વિકર્ણ તેનું બે …….. ત્રિકોણોમાં વિભાજન કરે છે.
( 4 ) Δ ABCમાં D અને E અનુક્રમે AB અને ACનાં મધ્યબિંદુ છે. જો BC = 8.2 સેમી હોય, તો DE = ……. સેમી.
( 5 ) Δ PQRની બાજુઓ PQ, QR અને RPનાં મધ્યબિંદુઓ અનુક્રમે X, Y અને Z છે. જો Δ XYZની પરિમિતિ 12.7 સેમી હોય, તો Δ PQRની પરિમિતિ ……. સેમી થાય.
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) સમાંતરબાજુ ચતુષ્કોણ ABCDમાં AB = 8 સેમી અને BC = 5 સેમી હોય, તો ABCDની પરિમિતિ શોધો.
( 2 ) Δ ABCની બાજુઓ AB, BC અને CAનાં મધ્યબિંદુઓ અનુક્રમે P, Q અને R છે, તો ચતુષ્કોણ PBCR કેવો ચતુષ્કોણ છે?
( 3 ) જે ચતુષ્કોણના સમાન વિકર્ણો પરસ્પર કાટખૂણે દુભાગે, તે ચતુષ્કોણનો પ્રકાર જણાવો.
( 4 ) ચતુષ્કોણ ABCDમાં ∠A : ∠B : ∠C : ∠D = 3 : 4 : 5 : 6 હોય, તો ચતુષ્કોણના સૌથી નાના ખૂણાનું માપ શોધો.
( 5 ) લંબચોરસ ABCDમાં AB = 8 સેમી અને BC = 15 સેમી હોય, તો BD શોધો.
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) સમાંતરબાજુ ચતુષ્કોણ ABCDમાં ∠A = 75° હોય, તો ∠B = ……..
A. 75°
B. 150°
C. 15°
D. 105°
( 2 ) સમબાજુ ચતુષ્કોણ PQRSમાં SP = 14 સેમી હોય, તો તેની પરિમિતિ ……. સેમી થાય.
A. 28
B. 42
C. 56
D. 70
( 3 ) જે ચતુષ્કોણના વિકર્ણો કાટખૂણે છેદે પરંતુ પરસ્પર દુભાગે નહીં તે ……. છે.
A. સમાંતરબાજુ ચતુષ્કોણ
B. સમલંબ ચતુષ્કોણ
C. સમબાજુ ચતુષ્કોણ
D. પતંગાકાર
( 4 ) સમાંતરબાજુ ચતુષ્કોણ ABCDમાં ∠A : ∠B : ∠C : ∠D = …… શક્ય છે.
A. 4 : 5 : 4 : 5
B. 3 : 4 : 5 : 6
C. 2 : 3 : 2 : 5
D. 1 : 2 : 3 : 4
( 5 ) સમબાજુ ચતુષ્કોણ PQRSના વિકર્ણો PR અને QS Mમાં છેદે છે, તો ∠PMQ = …….
A. 45°
B. 60°
C. 90°
D. 120°
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) લંબચોરસના સામસામેના ખૂણા પૂરક હોય છે.
( 2 ) દરેક લંબચોરસ એ ચોરસ પણ છે.
( 3 ) સમબાજુ ચતુષ્કોણની બાજુઓનાં મધ્યબિંદુઓને ક્રમમાં જોડવાથી લંબચોરસ મળે.
( 4 ) પતંગાકારના વિકર્ણો પરસ્પર કાટખૂણે દુભાગે છે.
( 5 ) સમાંતરબાજુ ચતુષ્કોણના સામસામેના ખૂણા પૂરક હોય છે.
જવાબો
1. ( 1 ) દુભાગે ( 2 ) 360° ( 3 ) એકરૂપ ( 4 ) 4.1 ( 5 ) 25.4
2. ( 1 ) 26 સેમી ( 2 ) સમલંબ ચતુષ્કોણ ( 3 ) ચોરસ ( 4 ) 60° ( 5 ) 17 સેમી
3. ( 1 ) 105° ( 2 ) 56 ( 3 ) પતંગાકાર ( 4 ) 4:5:4:5 ( 5 ) 90°
4. ( 1 ) ખરું ( 2 ) ખોટું ( 3 ) ખરું ( 4 ) ખોટું ( 5 ) ખોટું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here