Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 11 રચનાઓ
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 11 રચનાઓ
સ્વાધ્યાય – 11.1
1. આપેલ કિરણના ઉદ્ભવબિંદુ પર 90° ના ખૂણાની રચના કરો અને પ્રમાણિત કરો.

રચનાના મુદ્દા :
( 1 ) કિરણ AB આપેલ છે. કિરણ ABને A તરફ લંબાવી રેખા MAB મેળવો.
( 2 ) કોઈ અનુકૂળ ત્રિજ્યા અને કેન્દ્ર A લઈ વર્તુળનું ચાપ દોરો, જે રેખા MABને X અને Yમાં છેદે.
(૩) 1/2 XYથી મોટી ત્રિજ્યા લઈને X અને પુને વારાફરતી કેન્દ્ર લઈ ચાપ દોરો, જે એકબીજાને P બિંદુમાં છેદે.
( 4 ) Pમાંથી પસાર થાય તેવું કિરણ AC દોરો.
આમ, ∠CAB માગ્યા મુજબનો 90°નો ખૂણો છે.
રચનાને પ્રમાણિત કરીએ :
PX અને PY દોરો.
Δ PAX અને Δ PAYમાં,
AX = AY (એક જ વર્તુળની ત્રિજ્યાઓ)
PX = PY (સમાન વર્તુળની ત્રિજ્યાઓ)
PA = PA (સામાન્ય રેખાખંડ)
∴ બાબાબા મુજબ, Δ PAX = Δ PAY.
∴ ∠PAX = ∠PAY (CPCT)
પરંતુ, ∠PAX + ∠PAY = 180° (રેખિક જોડ)
∴ ∠PAY = 180°/2 = 90°
∴ ∠CAB = 90°
2. આપેલ કિરણના ઉદ્ભવબિંદુ પર 45ના ખૂણાની રચના કરો અને પ્રમાણિત કરો.
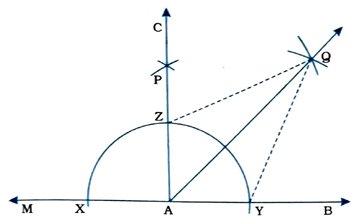
રચનાના મુદ્દા :
( 1 ) કિરણ AB આપેલ છે. કિરણ ABને A તરફ લંબાવી રેખા MAB મેળવો.
( 2 ) કોઈ સ્વૈર ત્રિજ્યા અને કેન્દ્ર A લઈ વર્તુળનું ચાપ ોરો, જે રેખા MABને X અને Yમાં છેદે.
( 3 ) 1/2 XYથી મોટી ત્રિજ્યા લઈને X અને Yને વારાફરતી કેન્દ્ર લઈ ચાપ ઘેરો, જે એક્બીજાને P બિંદુમાં છેદે.
( 4 ) Pમાંથી પસાર થાય તેવું કિરણ AC ઘેરો. આથી આપણને 90નો ∠CAB મળ્યો.
( 5 ) સૌપ્રથમ દોરેલ A કેન્દ્રિત ચાપ અને કિરણ ACના છેદબિંદુને Z નામ આપો.
( 6 ) 1/2 YZથી મોટી ત્રિજ્યા લઈને Y અને zને વારાફરતી કેન્દ્ર લઈ ચાપ દોરો, જે એકબીજાને Q બિંદુમાં છેદે.
( 7 ) કિરણ AQ રચો.
આમ, ∠QAB માગ્યા મુજબનો 45નો ખૂણો છે.
રચનાને પ્રમાણિત કરીએ :
દાખલા નં. 1માં આપણે ∠CAB = 90° પ્રમાણિત કરી ચૂક્યા છીએ, તેથી અહીં તેનું પુનરાવર્તન નહિ કરીએ.
રેખાખંડ QZ અને QY દોરી, Δ AZQ અને Δ AYQ મેળવો.
Δ AYQ અને Δ AZQમાં,
AY = AZ (એક જ વર્તુળની ત્રિજ્યાઓ)
YQ = ZQ (સમાન વર્તુળની ત્રિજ્યાઓ)
AQ = AQ (સામાન્ય રેખાખંડ)
∴ બાબાબા મુજબ, Δ AYQ = Δ AZQ
∴ ∠QAY = ∠QAZ (CPCT)
પરંતુ, ∠QAY + ∠QAZ = ∠ZAY = ∠CAB = 90°
∴ ∠QAY = 90°/2 = 45°
∴ ∠QAB = 45°
3. નીચે આપેલા માપના ખૂણાઓની રચના કરોઃ
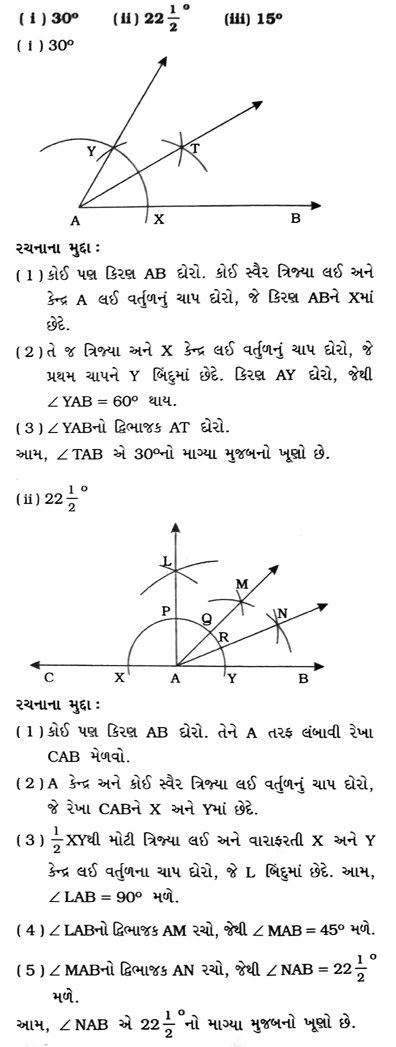

રચનાના મુદ્દા :
( 1 ) કોઈ પણ કિરણ AB દોરો. કોઈ સ્વૈર ત્રિજ્યા લઈ અને કેન્દ્ર A લઈ વર્તુળનું ચાપ દોરો, જે કિરણ ABને Xમાં છેદે.
( 2 ) તે જ ત્રિજ્યા અને X કેન્દ્ર લઈ વર્તુળનું ચાપ દોરો, જે પ્રથમ ચાપને Y બિંદુમાં છેદે. કિરણ AY દોરો, જેથી ∠YAB = 60 થાય.
( 3 ) ∠YABનો દ્વિભાજક AL રચો, જેથી ∠LAB = 30° થાય.
( 4 ) ∠LABનો દ્વિભાજક AM રચો, જેથી ∠MAB = 15° થાય.
આમ, ∠MAB એ 15નો માગ્યા મુજબનો ખૂણો છે.
4. નીચે આપેલ ખૂણાઓ રચો અને કોણમાપક વડે માપીને ચકાસો :
( i ) 75°
(ii) 105°
(iii) 135°
( i ) 75° અને
(ii) 105°

રચનાના મુદ્દા :
( 1 ) કોઈ પણ કિરણ AB દોરો. તેને A તરફ લંબાવી રેખા CAB મેળવો. કોઈ સ્વૈર ત્રિજ્યા અને A કેન્દ્ર લઈ વર્તુળનું ચાપ દોરો, જે રેખા CABને X અને Yમાં છેદે.
( 2 ) 1/2 XYથી મોટી ત્રિજ્યા લઈ અને વારાફરતી X અને Y કેન્દ્ર લઈ વર્તુળના ચાપ દોરો, જે L બિંદુમાં છેદે. કિરણ AL દોરો. આમ, ∠LAB = 90° મળે.
( 3 ) Xને કેન્દ્ર અને AX જેટલી ત્રિજ્યા લઈ વર્તુળનું ચાપ દોરો, જે ચાપ XYને Zમાં છેદે.
( 4 ) કિરણ AZ દોરો, જેથી ∠ZAB = 60° થાય.
( 5 ) હવે, ∠LAZનો દ્વિભાજક AM રચો. આથી ∠MAB = 75° અને ∠MAC = 105° થાય.
આમ, ∠MAB એ 75નો અને ∠MAC એ 105°નો એમ બે માગેલ ખૂણા એકસાથે મળે.
(iii) 135°
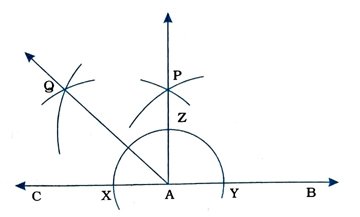
રચનાના મુદ્દા :
( 1 ) રેખા CAB દોરો. A કેન્દ્ર અને કોઈ સ્વૈર ત્રિજ્યા લઈને વર્તુળનું ચાપ દોરો, જે રેખા CABને X અને Yમાં છેદે.
( 2 ) 1/2 XYથી મોટી ત્રિજ્યા લઈને X અને Yને વારાફરતી કેન્દ્ર લઈ ચાપ દોરો, જે એકબીજાને P બિંદુમાં છેદે.
( 3 ) કિરણ AP દોરો. આમ, ∠PAC = ∠PAB = 90° મળે.
( 4 ) ∠PACનો દ્વિભાજક AQ રચો.
( 5 ) આથી ∠QAB = 135° થશે.
આમ, ∠QAB માગ્યા મુજબનો 135°નો ખૂણો છે.
5. આપેલ બાજુઓના માપવાળા સમબાજુ ત્રિકોણની રચના કરી તેની યથાર્થતા દર્શાવો.
રેખાખંડ XY આપેલ છે. એવા સમબાજુ ત્રિકોણની રચના કરવાની છે, જેમાં દરેક બાજુનું માપ XYના માપ જેટલું થાય.

રચનાના મુદ્દા :
( 1 ) કોઈ પણ કિરણ BM દોરો.
( 2 ) B કેન્દ્ર અને XY ત્રિજ્યા લઈ વર્તુળનું ચાપ દોરો, જે કિરણ BMને Cમાં છેદે.
( 3 ) XY ત્રિજ્યા લઈ B અને Cને વારાફરતી કેન્દ્ર લઈ વર્તુળના ચાપ દોરો, જે પરસ્પર A બિંદુમાં છેદે.
( 4 ) AB અને AC રચો.
આમ, Δ ABC એ માંગેલ સમબાજુ ત્રિકોણ છે, જેમાં દરેક બાજુનું માપ XYના માપ જેટલું છે.
રચનાની યથાર્થતા દર્શાવીએઃ
B કેન્દ્ર અને XY ત્રિજ્યા લઈને દોરેલું વર્તુળ કિરણ BMને Cમાં છેદે છે. માટે BC = XY થાય. B કેન્દ્ર અને XY ત્રિજ્યાવાળું વર્તુળ તથા C કેન્દ્ર અને XY ત્રિજ્યાવાળું વર્તુળ Aમાં છેદે છે. માટે AB = XY અને AC = XY થાય.
આમ, Δ ABCમાં AB = BC = AC = XY થાય.
આથી Δ ABC સમબાજુ ત્રિકોણ છે, જેની બાજુઓનું માપ આપ્યા મુજબ XY છે.
નોંધ : જો બાજુઓનું માપ આંકડાકીય રીતે આપેલ હોય. દા. ત., 4 સેમી, 5 સેમી વગેરે, તો સીધી પટ્ટીને બદલે અંકિત પટ્ટીનો ઉપયોગ કરવો પડે.
સ્વાધ્યાય – 11.2
1. BC = 7 સેમી, ∠B = 75° અને AB + AC = 13 સેમી હોય તેવા ત્રિકોણ ABCની રચના કરો.
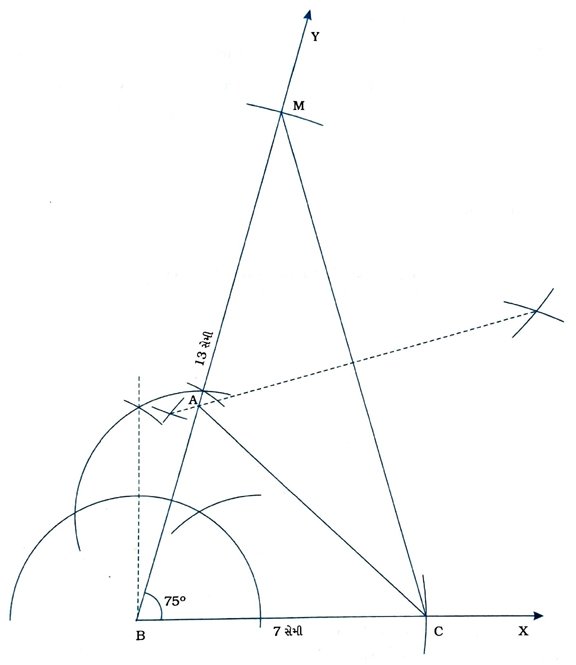
રચનાના મુદ્દા :
( 1 ) કિરણ BX દોરો. B કેન્દ્રિત 7 સેમી ત્રિજ્યાવાળો ચાપ દોરો, જે BXને Cમાં છેદે.
( 2 ) બિંદુ B આગળ ∠YBC રચો, જેનું માપ 75° થાય.
( 3 ) B કેન્દ્રિત 13 સેમી ત્રિજ્યાવાળો ચાપ દોરો, જે કિરણ BYને Mમાં છેદે.
( 4 ) MC દોરો અને તેનો લંબદ્વિભાજક રચો, જે BMને Aમાં છેદે.
( 5 ) AC દોરો.
આમ, Δ ABC એ આપેલ માપવાળો ત્રિકોણ છે.
2. BC = 8 સેમી, ∠B = 45° અને AB – AC = 3.5 સેમી હોય તેવા ત્રિકોણ ABCની રચના કરો.
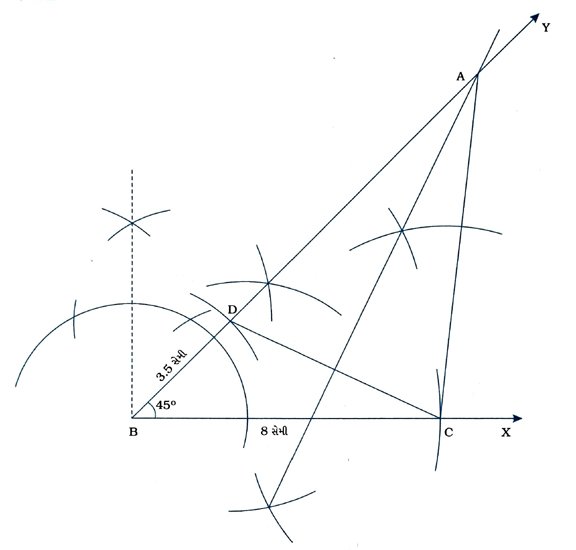
રચનાના મુદ્દા :
( 1 ) કિરણ BX દોરીને 8 સેમી લંબાઈનો રેખાખંડ BC મેળવો.
( 2 ) બિંદુ B આગળ કિરણ BYની રચના કરો, જેથી ∠ YBC = 45° થાય.
( 3 ) B કેન્દ્ર અને 3.5 સેમી ત્રિજ્યાવાળો ચાપ દોરો, જે કિરણ BYને Dમાં છેદે.
( 4 ) રેખાખંડ DC દોરી તેનો લંબદ્વિભાજક રચો, જે કિરણ BYને Aમાં છેદે.
( 5 ) રેખાખંડ AC દોરો.
આમ, Δ ABC એ આપેલ માપવાળો ત્રિકોણ છે.
3. QR = 6 સેમી, ∠Q = 60° અને PR – PQ = 2 સેમી હોય તેવા ત્રિકોણ PQRની રચના કરો.
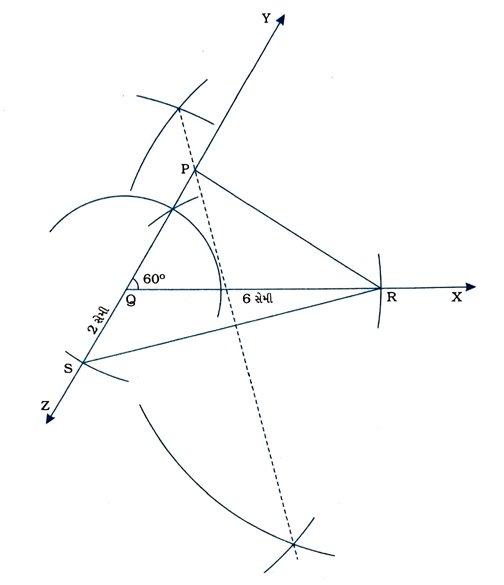
રચનાના મુદ્દા :
( 1 ) કિરણ QX દોરીને 6 સેમી લંબાઈનો રેખાખંડ QR મેળવો.
( 2 ) બિંદુ આગળ કિરણ QYની રચના કરો, જેથી ∠YOR = 60° થાય.
( 3 ) કિરણ QYને Q તરફ લંબાવી કિરણ QZ દોરો અને તેની પર QS = 2 સેમી થાય તેવું બિંદુ S મેળવો.
( 4 ) રેખાખંડ RS દોરી તેનો લંબદ્વિભાજક રચો, જે કિરણ QYને Pમાં છેદે.
( 5 ) રેખાખંડ PR દોરો.
આમ, Δ PQR એ આપેલ માપવાળો ત્રિકોણ છે.
4. ∠Y = 30°, ∠Z = 90° અને XY + YZ + ZX = 11 સેમી હોય તેવા ત્રિકોણ XYZની રચના કરો.
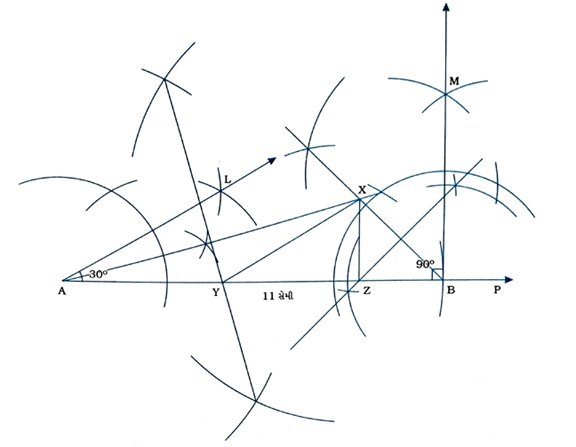
રચનાના મુદ્દા :
( 1 ) કિરણ AP દોરીને 11 સેમી લંબાઈનો રેખાખંડ AB મેળવો.
( 2 ) કિરણ AL એવું રચો, જેથી ∠LAB = 30° થાય.
( 3 ) કિરણ BM એવું રચો, જેથી ∠MBA 90° થાય.
( 4 ) ∠LAB અને ∠MBAના દ્વિભાજકો દોરો અને તેમનાં છેદબિંદુને X નામ આપો.
( 5 ) રેખાખંડ XB દોરો તથા તેનો લંબદ્વિભાજક રચો, જે ABને Zમાં છેદે.
( 6 ) રેખાખંડ XA દોરો તથા તેનો લંબદ્વિભાજક રચો, જે ABને Yમાં છે.
( 7 ) રેખાખંડ XY તથા XZ દોરો.
આમ, Δ XYZ એ આપેલ માપવાળો ત્રિકોણ છે.
5. પાયો 12 સેમી અને કર્ણ તથા બીજી બાજુનો સરવાળો 18 સેમી હોય તેવા કાટકોણ ત્રિકોણની રચના કરો.
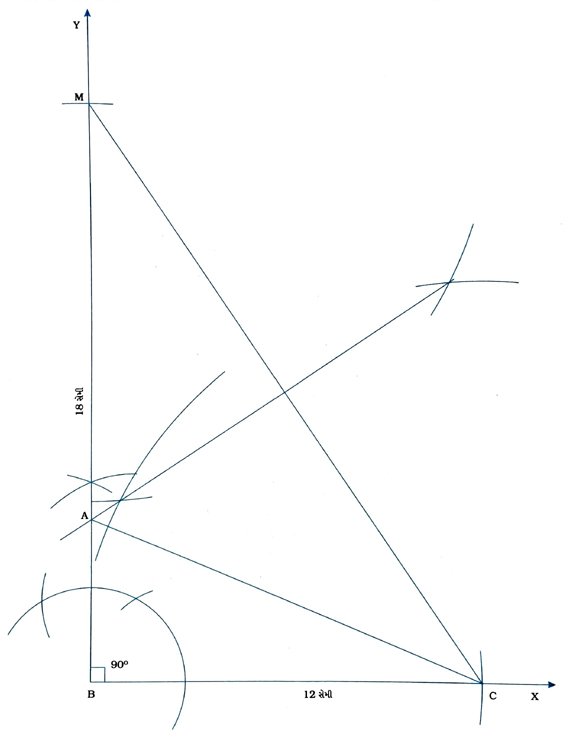
રચનાના મુદ્દા :
( 1 ) કિરણ BX દોરીને 12 સેમી લંબાઈનો રેખાખંડ BC મેળવો.
( 2 ) કિરણ BY એવું રચો, જેથી ∠YBC = 90° થાય.
( 3 ) B કેન્દ્ર અને 18 સેમી ત્રિજ્યાવાળો ચાપ દોરો, જે કિરણ BYને M બિંદુમાં છેદે.
( 4 ) રેખાખંડ CM દોરી તેનો લંબદ્વિભાજક રચો, જે BMને A બિંદુમાં છેદે.
( 5 ) રેખાખંડ AC રચો.
આમ, Δ ABC એ આપેલ માપવાળો કાટકોણ ત્રિકોણ છે. જેમાં ∠B કાટખૂણો છે, BC = 12 સેમી છે તથા AB + AC = 18 સેમી છે.
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here