NCERT Solutions Class 9Th Math – त्रिभुज
NCERT Solutions Class 9Th Math – त्रिभुज
लघु उत्तरीय प्रश्नोत्तर
1. दो त्रिभुजों के सर्वांगसम होने की भुजा-कोण-भुजा कसौटी को लिखें।
हल – यदि एक त्रिभुज की कोई दो भुजाएँ और उनके अंतर्गत कोण दूसरे त्रिभुज की कोई दो भुजाएँ और उनके अंतर्गत कोण के बराबर हों, तो वे त्रिभुज सर्वांगसम होते हैं ।
2. दो त्रिभुजों के सर्वांगसम होने की कोण-भुजा-कोण कसौटी को लिखें।
हल – यदि एक त्रिभुज के दो कोण और एक भुजा दूसरे त्रिभुज की दो कोणों और उनके संगत भुजा के बराबर हों, तो वे त्रिभुज सर्वांगसम होते हैं।
3. दो त्रिभुजों के सर्वांगसम होने की भुजा-भुजा-भुजा कसौटी को लिखें।
हल – यदि एक त्रिभुज की तीन भुजाएँ, दूसरे त्रिभुज की तीन भुजाओं के समान हों, तो वे त्रिभुज सर्वांगसम होते हैं ।
4. दो त्रिभुजों के सर्वांगसम होने की समकोण-कर्ण-भुजा कसौटी को लिखें।
हल – यदि दो समकोण त्रिभुजों में, एक त्रिभुज का कर्ण और एक भुजा क्रमशः दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर हों, तो दोनों त्रिभुज सर्वांगसम होते हैं ।
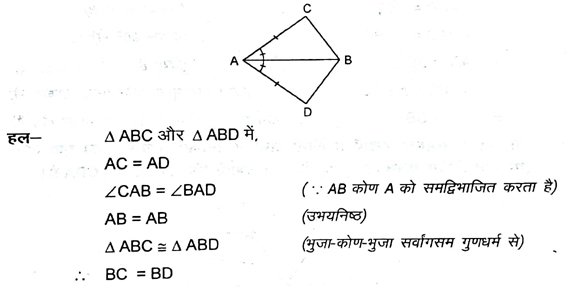
5. चतुर्भुज ACBD में, AC = AD है और AB कोण A को समद्विभाजित करता है (आकृति में) । दर्शाएँ कि ΔABC = ΔABD है।
BC और BD के बारे में आप क्या कह सकते हैं ?
6. ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB = ∠CBA है (आकृति में) सिद्ध करें कि –
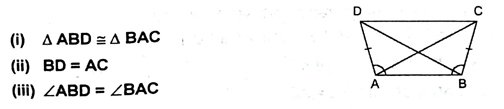

7. एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (आकृति में)। दर्शाएँ कि CD, रेखाखंड AB को समद्विभाजित करता है।

8. l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (आकृति में) । दर्शाएँ कि Δ ABC ≅ Δ CDA है ।
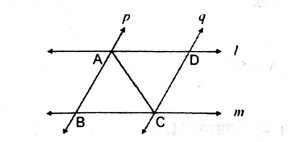
हल – चूँकि l तथा m समांतर रेखाएँ दूसरी समांतर रेखाओं p और q द्वारा प्रतिच्छेदित की जाती हैं। अतः AD || BC तथा AB ll CD
⇒ ABCD समांतर चतुर्भुज हैं।
अतः AB = CD और BC = AD

9. रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है । BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं (आकृति में) दर्शाएँ कि –

10. आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है । दर्शाएँ कि BC = DE है।

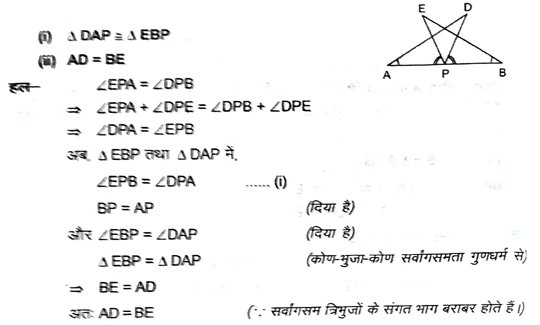
11. AB एक रेखाखंड है और p इसका मध्य बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (आकृति में) । दर्शाएँ कि –
12. एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (आकृति में) । दर्शाएँ कि –
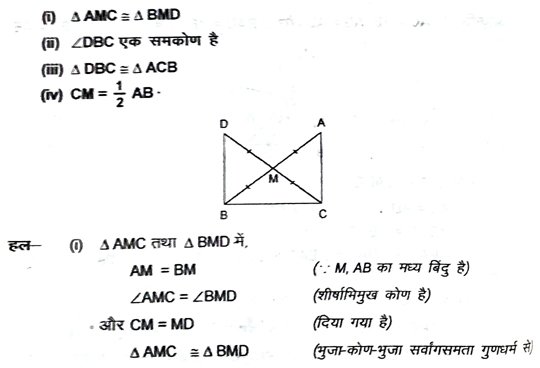

13. एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़ें। दर्शाएँ कि-


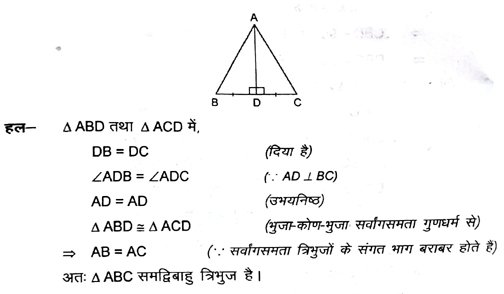
14. Δ ABC में AD भुजा BC का लम्ब समद्विभाजक है (देखें आकृति में) । दर्शाएँ कि Δ ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है ।
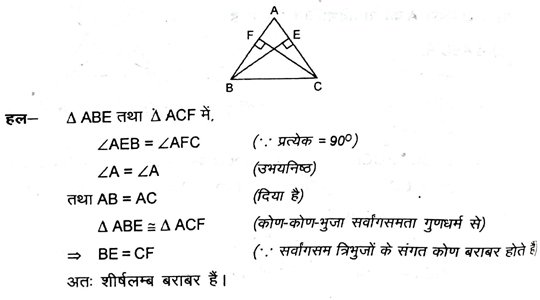
15. ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः BE और CF खींचे गए हैं (देखें आकृति) । दर्शाएँ कि ये शीर्षलम्ब बराबर हैं।
दीर्घ उत्तरीय प्रश्नोत्तर
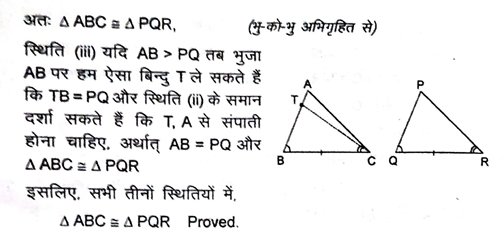
1. सिद्ध करें कि यदि एक त्रिभुज के कोई दो कोण और उनकी अंतर्गत भुजा दूसरे त्रिभुज के दो कोणों और उसकी अंतर्गत भुजा के बराबर हों, तो वे त्रिभुज सर्वांगसम होते हैं।

2. सिद्ध करें कि एक समद्विबाहु त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं ।
हल- दिया है— ABC एक समद्विबाहु त्रिभुज है जिनमें AB = AC

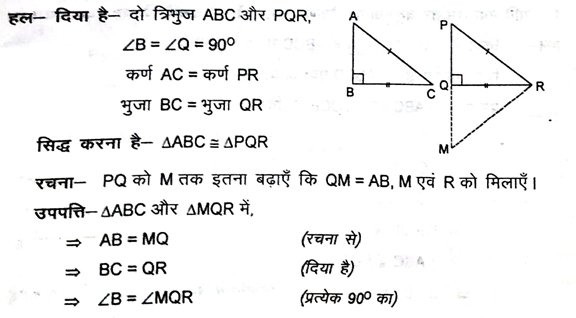
3. सिद्ध करें कि दो समकोण त्रिभुज सर्वांगसम होते हैं यदि त्रिभुज का कर्ण और एक भुजा क्रमश: दूसरे त्रिभुज के कर्ण और एक भुजा के बराबर होते हैं।

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here