Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 2 Polynomials (બહુપદીઓ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 2 Polynomials (બહુપદીઓ)
સ્વાધ્યાય – 2.1
1. નીચે આકૃતિમાં કોઈ બહુપદી p (x) માટે y = p (x)ના આલેખ આપેલ છે. દરેક કિસ્સામાં p (x)નાં શૂન્યોની સંખ્યા શોધો.
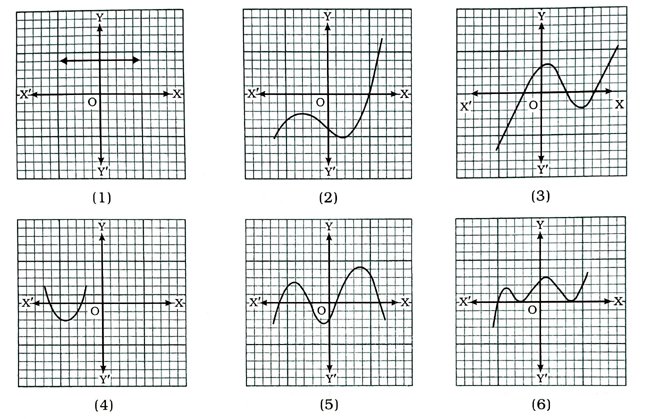
( 1 ) આલેખ x-અક્ષને સમાંતર હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 0 છે.
( 2 ) આલેખ x-અક્ષને એક બિંદુમાં છેદતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 1 છે.
( 3 ) આલેખ ૪-અક્ષને ત્રણ બિંદુમાં છેદતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 3 છે.
( 4 ) આલેખ x-અક્ષને બે બિંદુમાં છેદતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 2 છે.
( 5 ) આલેખ x-અક્ષને ચા૨ બિંદુમાં છેદતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 4 છે.
( 6 ) આલેખ x-અક્ષને ત્રણ બિંદુમાં છેદતો / સ્પર્શતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 3 છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. નીચેની આકૃતિમાં કોઈ બહુપદી p (x) માટે y = p (x)ના આલેખ આપેલ છે. દરેક કિસ્સામાં p (x)નાં શૂન્યોની સંખ્યા શોધો.
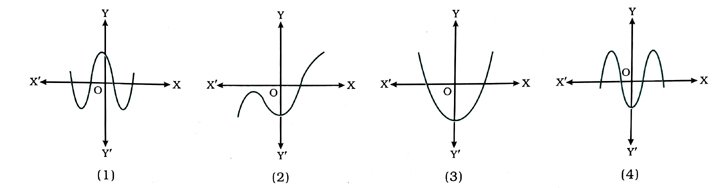
( 1 ) આલેખ x-અક્ષને ચાર બિંદુમાં છેદતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 4 છે.
( 2 ) આલેખ x-અક્ષને એક બિંદુમાં છેદતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 1 છે.
( 3 ) આલેખ x-અક્ષને બે બિંદુમાં છેદતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 2 છે.
( 4 ) આલેખ x-અક્ષને ચાર બિંદુમાં છેદતો હોવાથી બહુપદીનાં શૂન્યોની સંખ્યા 4 છે.
કૌશલ્ય ચકાસણી
1. નીચે આકૃતિમાં કોઈ બહુપદી p (x) માટે y = p (x)ના આલેખ આપેલ છે. દરેક કિસ્સામાં p (x)નાં શૂન્યોની સંખ્યા શોધો.
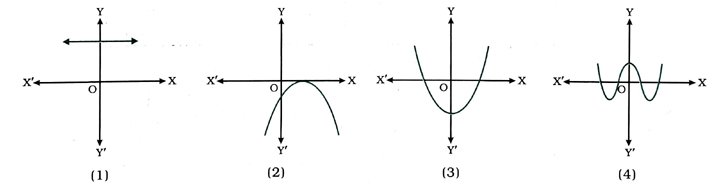
જવાબ : (1) 0 (2) 1 (3) 2 (4) 4
પાઠ્યપુસ્તકનાં ઉદાહરણો
2. દ્વિઘાત બહુપદી x2 + 7x + 10નાં શૂન્યો શોધો તથા તેનાં શૂન્યો અને સહગુણકો વચ્ચેનો સંબંધ ચકાસો.

3. બહુપદી x2 – 3નાં શૂન્યો શોધો અને તેનાં શૂન્યો અને સહગુણકો વચ્ચેનો સંબંધ ચકાસો.

4. જેનાં શૂન્યોના સરવાળો અને ગુણાકાર અનુક્રમે – 3 અને 2 હોય તેવી દ્વિઘાત બહુપદી મેળવો.

5. ચકાસો કે ૩, – 1, – 1/3 એ ત્રિઘાત બહુપદી p (x) = 3x3 – 5x2 – 11x – 3નાં શૂન્યો છે અને તે પછી શૂન્યો અને સહગુણકો વચ્ચેનો સંબંધ ચકાસો.
આપેલી બહુપદીને ax3 + bx2 + cx + d સાથે સરખાવતાં, આપણને a = 3, b = – 5, c = – 11, d = – 3 મળશે. હવે,
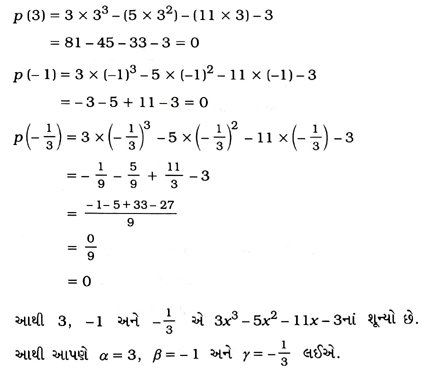
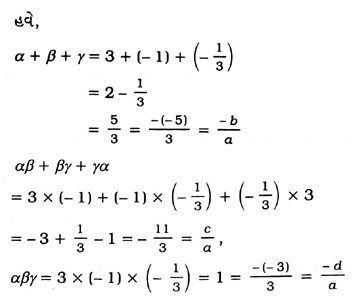
સ્વાધ્યાય – 2.2
1. નીચે દર્શાવેલ દ્વિઘાત બહુપદીઓનાં શૂન્યો શોધો તથા તેમનાં શૂન્યો અને સહગુણકો વચ્ચેનો સંબંધ ચકાસો :




2. નીચે દર્શાવેલ સંખ્યાઓ અનુક્રમે દ્વિઘાત બહુપદીનાં શૂન્યોનો સરવાળો અને શૂન્યોનો ગુણાકાર છે. તે પરથી દ્વિઘાત બહુપદી મેળવો :



મહત્ત્વનાં અન્ય ઉદાહરણો
1. નીચે દર્શાવેલ દ્વિઘાત બહુપદીઓનાં શૂન્યો શોધો તથા તેમનાં શૂન્યો અને સહગુણકો વચ્ચેનો સંબંધ ચકાસો :
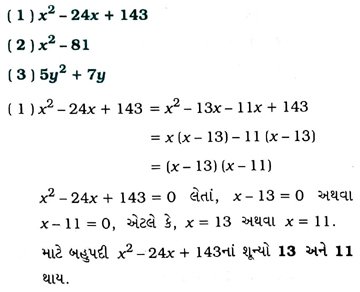


2. એવી દ્વિઘાત બહુપદી મેળવો જેનાં શૂન્યો 3 + √2 અને ૩ – √2 હોય.
ધારો કે, માગેલ દ્વિઘાત બહુપદી ax2 + bx + c છે જેનાં શૂન્યો α = 3 + √2 અને β = 3 – √2 છે.
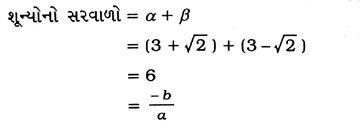


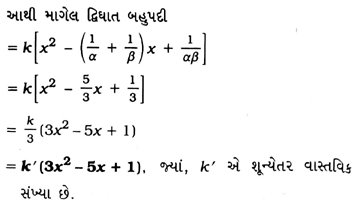
પાઠ્યપુસ્તકનાં ઉદાહરણો
6. 2x2 + 3x + 1ને x + 2 વડે ભાગો.

7. 3x3 + x2 + 2x + 5ને 1 + 2x + x2 વડે ભાગો.
સૌપ્રથમ આપણે ભાજક અને ભાજ્યના પદોને તેના ઘાતાંકના ઊતરતા ક્રમમાં ગોઠવીએ. યાદ કરો કે, બહુપદીના પદોને આ ક્રમમાં ગોઠવીએ તો, તે સ્વરૂપને બહુપદીનું પ્રમાણિત સ્વરૂપ કહે છે. આ ઉદાહરણમાં, ભાજ્ય પ્રમાણિત સ્વરૂપમાં જ છે અને x2 + 2x + 1 એ ભાજકનું પ્રમાણિત સ્વરૂપ થશે.
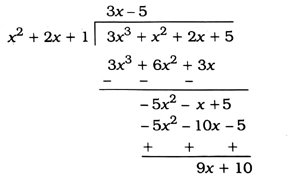
સોપાન 1 :
ભાગફળનું પ્રથમ પદ મેળવવા માટે ભાજ્યની સૌથી મોટી ઘાતવાળા પદને (એટલે કે 3x3) ભાજકના સૌથી મોટી ઘાતવાળા પદ (એટલે કે x2) વડે ભાગો. ભાગફળ 3x થશે. ત્યારબાદ ભાગાકારની પ્રક્રિયા આગળ ધપાવતાં – 5x2 − x + 5 વધશે.
સોપાન 2 :
હવે, ભાગળનું બીજું પદ મેળવવા માટે ભાગાકારના નવા ભાજ્યની સૌથી મોટી ઘાતવાળા પદને (એટલે કે – 5x2) ભાજકના સૌથી મોટી ઘાતવાળા પદ (એટલે કે x2) વડે ભાગો. ભાગફળ –5 મળશે. ફરીથી ભાગાકારની પ્રક્રિયા – 5x2 − x + 5 સાથે આગળ ધપાવો.
સોપાન 3:
9x + 10 બાકી રહેશે. હવે, 9x + 10ની ઘાત ભાજક x2 + 2x + 1ની ઘાત કરતાં ઓછી છે. માટે, આપણે ભાગાકાર આગળ ધપાવી શકીશું નહીં.
આથી ભાગફળ 3x – 5 અને શેષ 9x + 10 છે.
8. 3x2 – x3 – 3x + 5નો x – 1 − x2 વડે ભાગાકાર કરો અને ભાગપ્રવિધિ ચકાસો.
જુઓ કે, આપેલ બહુપદીઓ પ્રમાણિત સ્વરૂપમાં નથી. આથી ભાગાકાર કરવા માટે આપણે પ્રથમ ભાજ્ય અને ભાજકને તેની ઘાતના ઊતરતા ક્રમમાં ગોઠવીશું.

હવે, નવા ભાગફળ (3)ની ઘાત = 0 < ભાજક (– x2 + x – 1)ની ઘાત = 2 હોવાથી આપણે અટકીશું.
આથી ભાગફળ = x – 2; શેષ = 3 છે.
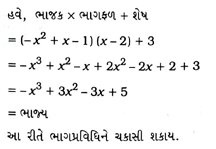
9. જો √2 અને − √2 એ 2x4 -3x3 – 3x2 + 6x – 2નાં બે શૂન્યો છે તેવું તમે જાણતા હો, તો બાકીનાં શૂન્યો શોધો.

સ્વાધ્યાય – 2.3
1. નીચે આપેલ તમામ બહુપદી p (x)ને બહુપદી g (x) વડે ભાગો અને ભાગફળ તથા શેષ મેળવો :

2. નીચે આપેલ બે બહુપદીઓ પૈકી બીજી બહુપદીને પ્રથમ બહુપદી વડે ભાગીને ચકાસો કે, પ્રથમ બહુપદી એ બીજી બહુપદીનો અવયવ છે કે નહીં :


4. x3 – 3x2 + x + 2ને બહુપદી g (x) વડે ભાગતા ભાગફળ અને શેષ અનુક્રમે x – 2 અને − 2x + 4 મળે છે, તો g (x) શોધો.
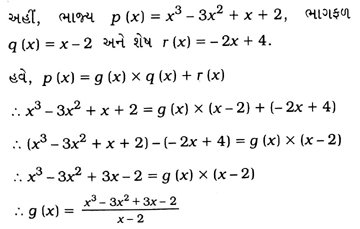
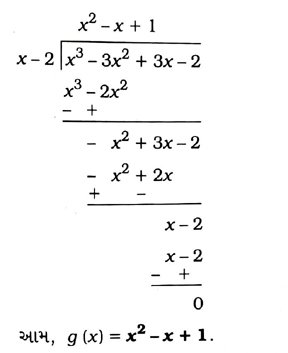
5. ભાગપ્રવિધિ અને નીચેની શરતોને સંતોષે તેવી બહુપદીઓ P (x), g (x), q (x) અને r (x)નાં ઉદાહરણો આપો :
(1) p (x)ની ઘાત = q (x)ની ઘાત
(2) q (x)ની ઘાત = r (x)ની ઘાત
(3) r (x)ની ઘાત = 0
( 1 ) p (x)ની ઘાત = q (x)ની ઘાત હોવાથી g (x)ની ઘાત = 0 થાય, એટલે કે g (x) એ શૂન્યેતર અચળ હોય તેવું એક ઉદાહરણ નીચે મુજબ આપી શકાય :
p (x) = 3x2 + 15x + 13, g (x) = 3,
q (x) = x2 + 5x + 4 અને r (x) = 1.
આપેલ ઉદાહરણ નીચે મુજબ ભાગપ્રવિધિનું સમાધાન કરે છેઃ
3x2 + 15x + 13 = 3 (x2 + 5x + 4) + 1
( 2 ) q (x)ની ઘાત = r (x)ની ઘાત હોવાથી,
g (x)ની ઘાત > q (૪)ની ઘાત, કારણ કે
g (x)ની ઘાત > r (x)ની ઘાત.
તેવું એક ઉદાહરણ નીચે મુજબ આપી શકાય :
p (x) = x3 + 5x2 + 2x + 7, g (x) = x2 + 1,
q (x) = x + 5 અને r (x) = x + 2.
આપેલ ઉદાહરણ નીચે મુજબ ભાગપ્રવિધિનું સમાધાન કરે છેઃ
x3 + 5x2 + 2x + 7 = (x2 + 1) (x + 5) + (x + 2).
( 3 ) r (x)ની ઘાત = 0 હોવાથી શેષ અચળ પદ છે તેવું એક ઉદાહરણ નીચે મુજબ આપી શકાય :
p (x) = x3 + 4x2 + 5x + 9, g (x) = x + 3,
q (x) = x2 + x + 2 અને r (x) = 3.
આપેલ ઉદાહરણ નીચે મુજબ ભાગપ્રવિધિનું સમાધાન કરે છેઃ
x3 + 4x2 + 5x + 9 = (x + 3) (x2 + x + 2) + 3
નોંધ : ઉપરોક્ત ત્રણેય દાખલાઓમાં અન્ય ઘણા ઉકેલ આપી શકાય.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. બહુપદી p (x) = x4 + 5x3 + 10x2 + 16x + 7ને બહુપદી g (x) = x2 + 2x +3 વડે ભાગતાં શેષ બહુપદી ax + b મળે છે. હ અને ની કિંમતો શોધો.
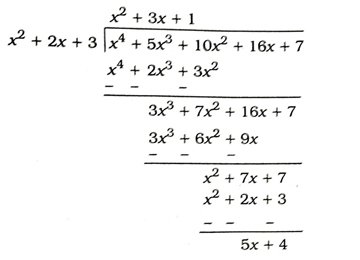
અહીં, શેષ 5x + 4 મળે છે. મળતી શેષ 5x + 4ને આપેલ શેષ ax + b સાથે સરખાવતાં, a = 5 અને b = 4 મળે,
2. જો બહુપદી 3x3 + 14x2 + 9x + aને બહુપદી 3x + 5 વડે નિઃશેષ ભાગી શકાતી હોય, તો તેની કિંમત શોધો.
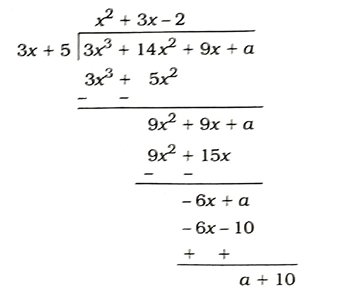
બહુપદી 3x3 + 14x2 + 9x + aને બહુપદી 3x + 5 વડે નિઃશેષ ભાગી શકાતી હોય, તો શેષ = 0 હોય.
∴ a + 10 = 0
∴ a = – 10
સ્વાધ્યાય – 2.4
આ સ્વાધ્યાય પરીક્ષાના માટે ધ્યાનમાં લેવાનું નથી.
1. નીચે ત્રિઘાત બહુપદીની સાથે દર્શાવેલ સંખ્યાઓ તેનાં શૂન્યો છે તે ચકાસો. દરેક પ્રશ્નમાં શૂન્યો અને સહગુણકો વચ્ચેનો સંબંધ પણ ચકાસો :


2. જેનાં શૂન્યોનો સરવાળો, બબ્બે શૂન્યોનાં ગુણાકારનો સરવાળો અને ગુણાકાર અનુક્રમે 2, −7, − 14 છે એવી ત્રિઘાત બહુપદી શોધો.
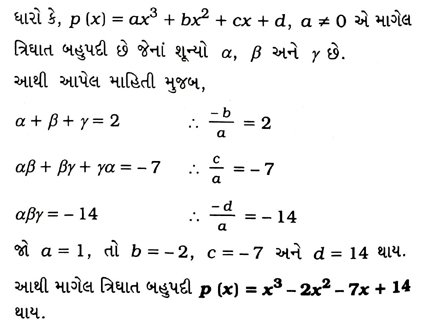
3. જો બહુપદી x3 – 3x2 + x + 1નાં શૂન્યો a − b, a, a + b, હોય, તો a અને b શોધો.
આપેલ ત્રિઘાત બહુપદી x3 – 3x2 + x + 1 માટે,
A = 1, B = – 3, C = 1 અને D = 1.
બહુપદીનાં શૂન્યો a – b, a અને a + b આપેલ છે.
હવે, શૂન્યોનો સરવાળો = (a – b) + a + (a + b) = 3a. બહુપદીનાં સહગુણકો પરથી,

4. બહુપદી x4 – 6x3 – 26x2 + 138x – 35નાં બે શૂન્યો 2 ± √3 હોય, તો બાકીના શૂન્યો શોધો.

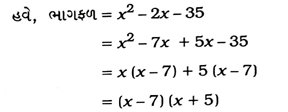
x – 7 = 0 લેતાં x = 7 અને x + 5 = 0 લેતાં x = – 5 આમ, આપેલ બહુપદીનાં બાકીનાં બે શૂન્યો 7 અને – 5 છે.

હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
( 1 ) સુરેખ બહુપદી p (x) = 3x + 2નું શૂન્ય = ……. છે.
( 2 ) દ્વિઘાત બહુપદી p (x) = x2 – 7x + 12નાં શૂન્યોનો ગુણાકાર …….. થાય.
( 3 ) ત્રિધાત બહુપદી p (x) = 2x3 – 17x2 + 38x – 15નાં શૂન્યોનો સરવાળો ……… થાય.
( 4 ) જો બહુપદી p (x) = x3 + 3x2 + kx – 24નું એક શૂન્ય 3 હોય, તો k = ……..
( 5 ) જો દ્વિઘાત બહુપદી p (x) = x2 + (k−7) x + (k + 1)નાં શૂન્યોનો સરવાળો અને શૂન્યોનો ગુણાકાર સમાન હોય, તો k = ………
( 6 ) નીચેના આલેખ x = p(y) માટે શૂન્યોની સંખ્યા ………. છે.
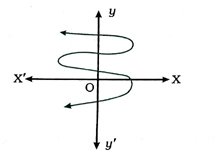
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
( 1 ) નીચે આપેલ બહુપદી p (x)ના આલેખ મુજબ p (x)નાં − 1 અને +1 વચ્ચે રહેલાં શૂન્યોની સંખ્યા ………. છે.
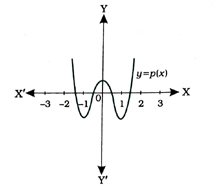
A. 4
B. 3
C. 2
D. 1
( 2 ) જેનાં શૂન્યોનો સરવાળો અને ગુણાકાર અનુક્રમે 4 અને 4 હોય તેવી દ્વિઘાત બહુપદી …….. છે.
A. x2 – 4x – 4
B. x2 + 4x + 4
C. x2 + 4x – 4
D. x2 – 4x + 4

3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ આપો :
( 1 ) દ્વિઘાત બહુપદી x2 − 12x + 20નાં શૂન્યોનો સરવાળો કેટલો થાય?
( 2 ) જો ત્રિઘાત બહુપદી ax3 + bx2 + cx + dનાં શૂન્યો પૈકી એક શૂન્ય 0 હોય, તો બાકીનાં બે શૂન્યોનો ગુણાકાર કેટલો થાય?
[સૂચન : જો y = 0, તો αβ + βγ + γα = αβ]
( 3 ) ત્રિઘાત બહુપદી p (x) = x3 + 5x2 – 2x – 24નાં શૂન્યોનો ગુણાકાર કેટલો થાય?
( 4 ) શું x6 + 2x3 + x – 1ને xની 5 ઘાતવાળી કોઈ બહુપદી વડે ભાગતા, ભાગફળ x2 – 1 થઈ શકે?
( 5 ) જો બહુપદી p (x)ને બહુપદી g (x) વડે ભાગતા ભાગફળ શૂન્ય મળે, તો p (x)ની ઘાત અને g (x)ની ઘાત વચ્ચેનો સંબંધ લખો.
( 6 ) y = 6x – 2x2 + 7નો આલેખ કેવો હશે?
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) જો કોઈ બહુપદીનો આલેખ x-અક્ષને ફક્ત એક જ બિંદુમાં છેદે, તો તે બહુપદી દ્વિઘાત બહુપદી ન હોઈ શકે.
( 2 ) જો કોઈ ત્રિઘાત બહુપદીનાં બે શૂન્યોની કિંમત 0 હોય, તો તે બહુપદીમાં xવાળું પદ અને અચળ પદ ન હોય.
[સૂચન : αβ + βγ + γα = 0 અને αβγ = 0 ]
( 3 ) 2 એ બહુપદી p (x) = x2 – 6x + 8નું એક શૂન્ય છે.
( 4 ) 5 એ બહુપદી p (x) = 2x3 – 5x2 – 13x + 30નું એક શૂન્ય છે.
( 5 ) જો 3 એ બહુપદી p (x) = x2 – 11x + kનું એક શૂન્ય હોય, તો k = 24.

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here