Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 3 Pair of Linear Equations in Two Variables (દ્વિચલ સુરેખ સમીકરણયુગ્મ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 3 Pair of Linear Equations in Two Variables (દ્વિચલ સુરેખ સમીકરણયુગ્મ)
સ્વાધ્યાય – 3.1
1. આફતાબ તેની દીકરીને કહે છે, “સાત વર્ષ પહેલાં મારી ઉંમર તે વખતની તારી ઉંમર કરતાં સાત ગણી હતી. હવે પછીના ત્રણ વર્ષ પછી મારી ઉંમર તારી તે વખતની ઉંમર કરતાં ત્રણ ગણી હશે.’’ (શું આ રસપ્રદ છે ?) આ પરિસ્થિતિને બૈજિક રીતે અને આલેખની રીતે દર્શાવો.
ધારો કે, આફતાબની હાલની ઉંમર ૪ વર્ષ અને તેની દીકરીની હાલની ઉંમર પુ વર્ષ છે, તો સાત વર્ષ પહેલાં આફતાબની ઉંમ૨ x-7 વર્ષ અને તેની દીકરીની ઉંમર y−7 વર્ષ હતી.
આથી આપેલ માહિતી મુજબ,
x – 7 = 7 (y –7)
∴ x − 7 = 7y – 49
∴ x — 7y + 42 = 0 …….. (1)
તે જ રીતે, ત્રણ વર્ષ બાદ આફતાબની ઉંમર x + 3 વર્ષ અને તેની દીકરીની ઉંમર y + 3 વર્ષ થશે.
આથી આપેલ માહિતી મુજબ,
x + 3 = 3 (y + 3)
∴ x + 3 = 3y + 9
∴ x – 3y – 6 = 0 …….. (2)
આમ, સમીકરણો x−7y + 42 = 0 અને x – 3y – 6 = 0 એ આપેલ પરિસ્થિતિને બેજિક રીતે દર્શાવે છે.
આપેલ પરિસ્થિતિને આલેખની રીતે દર્શાવવા આપણે બંને સમીકરણોના આલેખ એક જ આલેખપત્ર પર દોરીએ.


ઉપરોક્ત આલેખ આપેલ પરિસ્થિતિને આલેખની રીતે દર્શાવે છે.
તમે જોઈ શકો છો કે, બંને રેખા બિંદુ (42, 12)માં છેદે છે.
2. ક્રિકેટ-ટીમના પ્રશિક્ષક ₹ 3900માં 3 બેંટ અને 6 દડા ખરીદે છે. પછી તે બીજું તે જ પ્રકારનું 1 બૅટ અને તે જ પ્રકારના વધુ 3 દડા ₹ 1300માં ખરીદે છે. આ પરિસ્થિતિને બૈજિક અને ભૌમિતિક રીતે દર્શાવો.
ધારો કે, એક બૅટની કિંમત ₹ x અને એક દડાની કિંમત ₹ y છે. આથી 3 બૅટની કુલ કિંમત ₹ 3x અને 6 દડાની કુલ કિંમત ₹ 6y થાય. આપેલ માહિતી મુજબ 3 બૅટ અને 6 દડાની કુલ કિંમત ₹ 3900 છે.
∴ 3x + 6y = 3900
∴ x + 2y = 1300
તે જ રીતે, 1 બૅટની કિંમત ₹ x અને ૩ દડાની કુલ કિંમત ૬ 3ઘુ થાય. આપેલ માહિતી મુજબ 1 બૅટ અને 3 દડાની કુલ કિંમત ₹ 1300 છે.
∴ x + 3y = 1300
આમ, સમીકરણો x + 2y = 1300 અને x + 3y = 1300 આપેલ પરિસ્થિતિને બેજિક રીતે દર્શાવે છે.
આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવવા આપણે બંને સમીકરણોના આલેખ એક જ આલેખપત્ર પર દોરીએ.

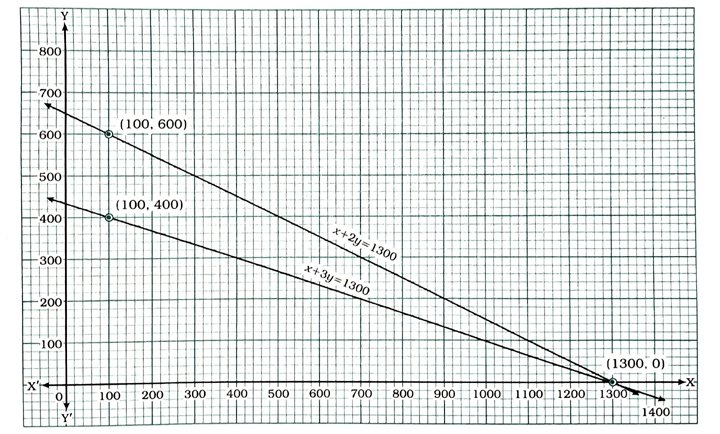
ઉપરોક્ત આલેખ આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવે છે.
તમે જોઈ શકો છો કે, બંને રેખા બિંદુ (1300, 0)માં છેદે છે.
3. એક દિવસે 2 કિગ્રા સફરજન અને 1 કિગ્રા દ્રાક્ષની કિંમત ₹ 160 હતી. એક મહિના પછી 4 કિગ્રા સફરજન અને 2કિગ્રા દ્રાક્ષની કિંમત ₹ 300 હતી. આ પરિસ્થિતિને બૈજિક રીતે અને ભૌમિતિક રીતે દર્શાવો.
ધારો કે, 1 કિગ્રા સફરજનની કિંમત ₹ x અને 1 કિગ્રા દ્રાક્ષની કિંમત ₹ y છે.
આથી આપેલ માહિતી મુજબ, 2x + y = 160 અને 4x + 2y = 300.
આમ, સમીકરણો 2x + y = 160 અને 4x + 2y = 300 એ આપેલ પરિસ્થિતિને બૈજિક રીતે દર્શાવે છે.
આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવવા આપણે બંને સમીકરણોના આલેખ એક જ આલેખપત્ર પર દોરીએ.


ઉપરોક્ત આલેખ આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવે છે.
તમે જોઈ શકો છો કે, બંને રેખા પરસ્પર સમાંતર છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. બે છોકરીઓની હાલની ઉંમરનો ગુણોત્તર 2: ૩ છે. ચાર વર્ષ બાદ તેમની ઉંમરનો ગુણોત્તર ૩: 4 થશે. આ પરિસ્થિતિને બૈજિક તેમજ ભૌમિતિક રીતે દર્શાવો.
ધારો કે, બે છોકરીઓ પૈકી નાની છોકરીની હાલની ઉંમર x વર્ષ અને મોટી છોકરીની હાલની ઉંમર y વર્ષ છે.
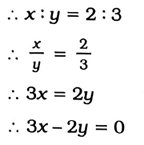
ચાર વર્ષ બાદ નાની છોકરીની ઉંમર x + 4 વર્ષ અને મોટી છોકરીની ઉંમર y + 4 વર્ષ થશે.

આમ, સમીકરણો 3x – 2y = 0 અને 4x – 3y = – 4 એ આપેલ પરિસ્થિતિને બૈજિક રીતે દર્શાવે છે.
આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવવા આપણે બંને સમીકરણોના આલેખ એક જ આલેખપત્ર પર દોરીએ.

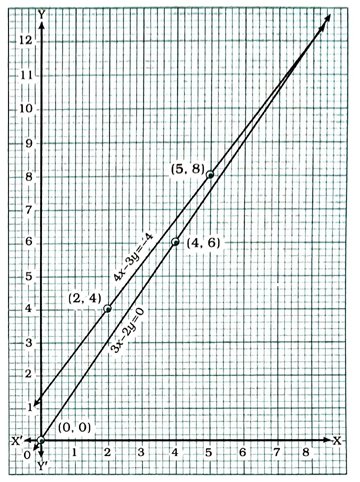
ઉપરોક્ત આલેખ આપેલ પરિસ્થિતિને ભૌમિતિક રીતે દર્શાવે છે.
તમે જોઈ શકો છો કે, બંને રેખા બિંદુ (8, 12)માં છેદે છે.
પાઠ્યપુસ્તકનાં ઉદાહરણો
4. સમીકરણયુગ્મ
x + 3y = 6 …….. (1)
2x – 3y = 12 …….. (2)
સુસંગત છે કે નહીં તે ચકાસો. જો સુસંગત હોય, તો આલેખની મદદથી ઉકેલો.
સમીકરણો (1) અને (2)ના આલેખ દોરીએ. આ માટે આપણે દરેક સમીકરણના બબ્બે ઉકેલ શોધીશું, જે નીચેના કોષ્ટકમાં દર્શાવેલ છે :

આલેખપત્ર ઉપર બિંદુઓ A (0, 2), B (6, 0), P (0, − 4) અને Q(3, – 2) દર્શાવો. આકૃતિમાં દર્શાવ્યા પ્રમાણે તેમને જોડતી રેખાઓ AB અને PQ દોરો.

બિંદુ B (6, 0) એ બંને રેખાઓ AB અને PQ ઉ૫૨નું સામાન્ય બિંદુ છે. તેથી સુરેખ સમીકરણયુગ્મનો ઉકેલ x = 6 અને y = 0 છે. આથી આપેલ સમીકરણયુગ્મ સુસંગત છે.
5. આલેખની રીતથી નીચેના સમીકરણયુગ્મને એક પણ ઉકેલ નથી, અનન્ય ઉકેલ છે અથવા અનંત ઉકેલો છે તે નક્કી કરો.

તે સમીકરણ (1)ને સમાન છે. સમીકરણો (1) અને (2) દર્શાવતી રેખાઓ સંપાતી છે તેમ તેમનું નિરૂપણ દર્શાવે છે. તેથી સમીકરણો (1) અને (2)ને અનંત ઉકેલો છે.
સમીકરણ (1) માટે,
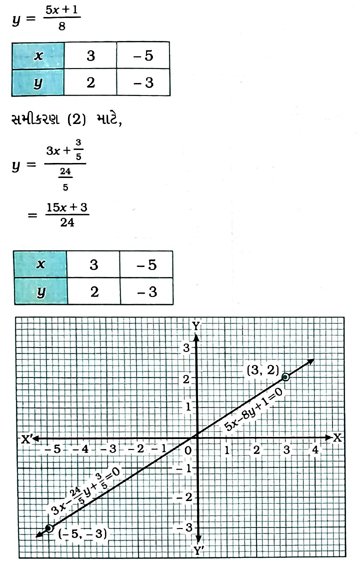
6. ચંપા ‘સેલ’માં કેટલાંક પેન્ટ અને સ્કર્ટ ખરીદવા ગઈ હતી. જ્યારે તેને તેના મિત્રોએ પૂછ્યું કે તેણે દરેકની કેટલી સંખ્યામાં ખરીદી કરી હતી, ત્યારે તેણે જવાબ આપ્યો, પેન્ટની સંખ્યાના બે ગણામાંથી બે ઓછી સંખ્યામાં સ્કર્ટ ખરીદ્યા. પણ પેન્ટની સંખ્યાના ચાર ગણામાંથી ચાર ઓછી સંખ્યામાં સ્કર્ટ ખરીદ્યા.’ ચંપાએ કેટલી સંખ્યામાં પેન્ટ અને કેટલી સંખ્યામાં સ્કર્ટ ખરીદ્યા તે શોધવા તેના મિત્રોને મદદ કરો.
ધારો કે, ખરીદેલા પેન્ટની સંખ્યા ૪ અને સ્કર્ટની સંખ્યા પુ છે. આથી સમીકરણો નીચે પ્રમાણે મળશે :
y = 2x – 2 …….. (1)
અને y = 4x – 4 …….. (2)
સમીકરણ (1) અને (2)ના બે ઉકેલોની મદદથી આલેખપત્ર પર આલેખ દોરો. કોષ્ટકમાં તેમના ઉકેલો આપેલા છે :
સમીકરણોના ઉકેલ સમાવતાં બિંદુઓમાંથી પસાર થતી રેખાઓ દર્શાવો. તે બે રેખાઓ બિંદુ (1, 0) આગળ છેદે છે. તેથી x = 1 અને y = 0 એ સુરેખ સમીકરણયુગ્મનો ઉકેલ થશે. એટલે કે તે 1 પેન્ટ ખરીદે છે અને સ્કર્ટ ખરીદતી નથી.
સ્વાધ્યાય – 3.2
1. નીચેની સમસ્યાઓ પરથી સુરેખ સમીકરણયુગ્મ બનાવો અને તેમનો ઉકેલ આલેખની રીતે શોધો :
( 1 ) ધોરણ Xના દસ વિદ્યાર્થીઓ ગણિતના કોયડાની સ્પર્ધામાં ભાગ લે છે. જો ભાગ લેનાર છોકરીઓની સંખ્યા છોકરાઓની સંખ્યા કરતાં 4 વધારે હોય, તો કેટલા છોકરાઓએ અને કેટલી છોકરીઓએ કોયડાની સ્પર્ધામાં ભાગ લીધો હશે તે શોધો.
( 2 ) 5 પેન્સિલ અને 7 પેનની કુલ કિંમત ₹ 50 છે અને તે જ કિંમતવાળી 7 પેન્સિલ અને 5 પેનની કુલ કિંમત ₹ 46 છે, તો એક પેન્સિલ અને એક પેનની કિંમત શોધો.
( 1 ) ધારો કે, x છોકરાઓ અને y છોકરીઓ સ્પર્ધામાં ભાગ લે છે.
આથી આપેલ માહિતી પરથી નીચે મુજબના બે સમીકરણ મળે :
x + y = 10 ……. (1)
અને y = x + 4,
એટલે કે, y − x = 4 …….. (2)
આ સમીકરણોના આલેખ દોરવા આપણે બંને સમીકરણના બે-બે ઉકેલ શોધીને કોષ્ટકમાં દર્શાવીએ.
સમીકરણ (1) માટે, x + y = 10 પરથી, y = 10 − x મળે.

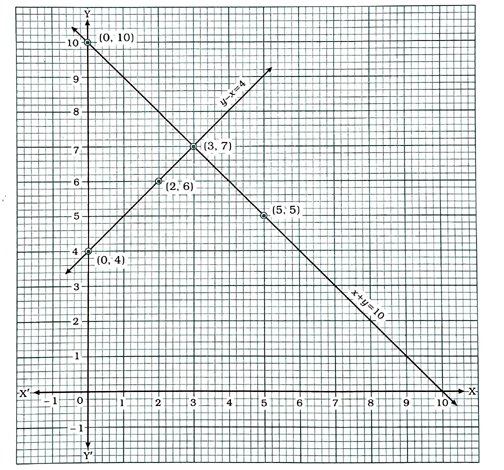
ઉપરોક્ત આલેખમાં બે રેખાઓ બિંદુ (3, 7)માં છેદે છે. આથી x = 3 અને y = 7 એ આપણે મેળવેલ સમીકરણયુગ્મનો ઉકેલ છે.
આમ, 3 છોકરાઓ અને 7 છોકરીઓ એ કોયડાની સ્પર્ધામાં ભાગ લીધો હશે.
ચકાસણી : x = 3 અને y = 7 એ પ્રશ્નમાં આપેલ બંને શરતોનું સમાધાન કરે છે.
( 2 ) ધારો કે, એક પેન્સિલની કિંમત ₹ x અને એક પેનની કિંમત ₹ y છે.
આથી આપેલ માહિતી પરથી નીચે મુજબના બે સમીકરણ મળે :
5x + 7y = 50 ……. (1)
7x + 5y = 46 ……. (2)
આ સમીકરણોના આલેખ દોરવા આપણે બંને સમીકરણના બે-બે ઉકેલ શોધીને કોષ્ટકમાં દર્શાવીએ.
સમીકરણ (1) માટે, 5x + 7y = 50 પરથી,


ઉપરોક્ત આલેખમાં બે રેખાઓ બિંદુ (3, 5)માં છેદે છે. આથી x = 3 અને y = 5 એ આપણે મેળવેલ સમીકરણયુગ્મનો ઉકેલ છે.
આમ, એક પેન્સિલની કિંમત ₹ 3 અને એક પેનની કિંમત ₹ 5 છે.
ચકાસણી : x = 3 અને y = 5 એ બંને સમીકરણ 5x + 7y = 50 અને 7x + 5y = 46નું સમાધાન કરે છે.



4. નીચેનાં પૈકી કયું સુરેખ સમીકરણયુગ્મ સુસંગત છે કે સુસંગત નથી, તે જણાવો. જો સુસંગત હોય, તો ભૌમિતિક રીતે ઉકેલ શોધો.


અહીં, બંને સમીકરણોની રેખાઓ સંપાતી છે. આથી તે સામાન્ય રેખા પરનું કોઈ પણ બિંદુ સમીકરણયુગ્મનો ઉકેલ આપે. આમ, y = 5 –x, જ્યાં x એ કોઈ વાસ્તવિક સંખ્યા છે, એ આપેલ સમીકરણયુગ્મના ઉકેલ છે.

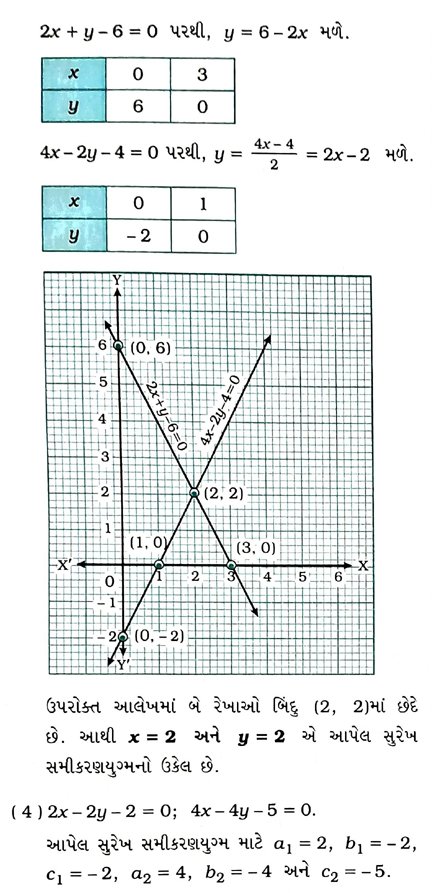


અહીં, બે રેખાઓ બિંદુ (20, 16)માં છેદે છે. આથી x = 20 અને y = 16 એ સમીકરણયુગ્મનો અનન્ય ઉકેલ છે.
આમ, બગીચાની લંબાઈ 20 મી અને પહોળાઈ 16મી છે.
6. સુરેખ સમીકરણ 2x + 39 – 8 = 0 આપેલ છે. એવું બીજું દ્વિચલ સુરેખ સમીકરણ લખો કે જેથી તે જોડીનું ભૌમિતિક નિરૂપણ નીચે પ્રમાણે હોય :
( 1 ) છેદતી રેખાઓ
( 2 ) સમાંતર રેખાઓ
( 3 ) સંપાતી રેખાઓ


7. સમીકરણો x – y + 1 = 0 અને 3x + 2y – 12 = 0 દ્વારા દર્શાવાતી રેખાઓના આલેખ દોરો. આ રેખાઓ અને x-અક્ષ દ્વારા રચાયેલા ત્રિકોણનાં શિરોબિંદુઓના યામ દર્શાવો અને બનતા ત્રિકોણાકાર પ્રદેશને છાયાંકિત કરો.
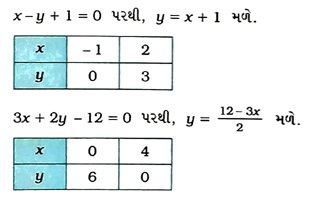

આપેલ રેખાઓ અને ૪-અક્ષ દ્વારા રચાયેલા ત્રિકોણનાં શિરોબિંદુઓ (– 1, 0), (4, 0) તથા (2, 3) છે.
મહત્ત્વનાં અન્ય ઉદાહરણો


આથી આપેલ સુરેખ સમીકરણયુગ્મ સુસંગત છે અને તે સમીકરણોને દર્શાવતી રેખાઓ ભિન્ન છેદતી રેખાઓ છે.
2. નીચેના સુરેખ સમીકરણયુગ્મનો ઉકેલ આલેખની રીતે શોધો :
x + y = 6 અને 3x – 4y = – 3
તદ્ઉપરાંત, તે સમીકરણોની રેખાઓ તથા x-અક્ષ દ્વારા બનતા ત્રિકોણનાં શિરોબિંદુઓ શોધો.


અહીં, બે રેખાઓ બિંદુ (3, 3)માં છેઠે છે. આથી આપેલ સુરેખ સમીકરણયુગ્મ x + y = 6 અને 3x – 4y = – 3નો અનન્ય ઉકેલ x = 3 અને y = 3 છે.
આપેલ સમીકરણોની રેખાઓ તથા x-અક્ષ દ્વારા બનતા ત્રિકોણના શિરોબિંદુઓ (3, 3), (– 1, 0) અને (6, 0) છે.
સ્વાધ્યાય – 3.3
1. નીચેનાં દ્વિચલ સુરેખ સમીકરણયુગ્મનો ઉકેલ આદેશની રીતે મેળવો :




2. 2x + 3y = 11 અને 2x – 4y = – 24નો ઉકેલ શોધો અને એવો ‘m’ શોધો કે જેથી y = mx + 3 થાય.

∴ 2m = – 2
∴ m = − 1
આમ, આપેલ સમીકરણયુગ્મનો ઉકેલ x = − 2, y = 5 છે અને m = − 1 એ y = mx + 3નું સમાધાન કરે છે.
3. નીચેની સમસ્યા ઉપરથી દ્વિચલ સુરેખ સમીકરણયુગ્મ મેળવો અને તેમનો ઉકેલ આદેશની રીતે મેળવો :
( 1 ) બે સંખ્યાનો તફાવત 26 છે અને એક સંખ્યા બીજી સંખ્યાથી ત્રણ ગણી છે, તો તે બે સંખ્યા શોધો.
ધારો કે, મોટી સંખ્યા x અને નાની સંખ્યા y છે.
આથી આપેલ માહિતી મુજબ નીચેના સમીકરણ મળે :
x – y = 26 ………(1)
x = 3y ……… (2)
સમીકરણ (1)માં x = 3y મૂકતાં,
3y – y = 26
∴ 2y = 26
∴ y = 13
x = 3yમાં y = 13 મૂકતાં,
x = 3 × 13 = 89.
આમ, માગેલ સંખ્યાઓ 39 અને 13 છે.
ચકાસણી : સંખ્યાઓનો તફાવત = 39 – 13 = 26 અને 39 એ 13ના ત્રણ ગણા છે.
( 2 ) બે પૂરકકોણો પૈકી મોટો ખૂણો નાના ખૂણા કરતાં 18° મોટો હોય, તો તે પૂરકકોણો શોધો.
ધારો કે, પૂરકકોણો પૈકી મોટા ખૂણાનું અંશમાપ x અને નાના ખૂણાનું અંશમાપ y છે.
આથી આપેલ માહિતી મુજબ નીચેના સમીકરણો મળે :
x + y = 180 …….(1)
x – y = 18 ……..(2)
સમીકરણ (2)માંથી x = y + 18 મળે.
સમીકરણ (1)માં x = y + 18 મૂકતાં,
y + 18 + y = 180
∴ 2y = 162
∴ y = 81
સમીકરણ (2)માં y = 81 મૂકતાં,
x – 81 = 18
∴ x = 99
આમ, માગેલ ખૂણાના અંશમાપ 99 અને 81 છે.
ચકાસણી : મોટો ખૂણો – નાનો ખૂણો = 99° – 81° = 18° અને મોટો ખૂણો + નાનો ખૂણો = 99° + 81° = 180° એટલે કે ખૂણા પૂરકકોણ છે.
(3) ક્રિકેટ-ટીમના કોચે 7 બૅટ અને 6 દડા ₹ 3800માં ખરીદ્યા. પછીથી તેણે તે જ કિંમતવાળા 3 બૅટ અને 5 દડા ₹ 1750માં ખરીદ્યા. તો એક બૅટની કિંમત અને એક દડાની કિંમત શોધો.
ધારો કે, એક બૅટની કિંમત ₹ x અને એક દડાની કિંમત ₹ y છે.
આથી આપેલ માહિતી મુજબ નીચેના સમીકરણો મળે :

(4) એક શહેરમાં ટેક્સીનું ભાડું નિશ્ચિત ભાડા અને અંતરના પ્રમાણમાં સંયુક્ત રીતે લેવાય છે. 10 કિમીના અંતર માટે ₹ 105 અને 15 કિમીની મુસાફરી માટે ₹ 155ની ચુકવણી કરવી પડે છે, તો નિશ્ચિત ભાડું કેટલું અને પ્રતિ કિમી કેટલા દરે કિંમત ચૂકવવી પડે? મુસાફરે 25 કિમીની મુસાફરી માટે કેટલું ભાડું ચૂકવવું પડશે?
ધારો કે, નિશ્ચિત ભાડું ₹ x અને મુસાફરીના દરેક કિલોમીટરદીઠ ભાડું ₹ y છે.
આથી આપેલ માહિતી મુજબ નીચેના સમીકરણો મળે :

( 5 ) એક અપૂર્ણાંકના અંશ અને છેદ બંનેમાં 2 ઉમેરતાં તે 9/11 બને છે. જો અપૂર્ણાંકના અંશ અને છેદ બંનેમાં 3 ઉમેરતાં તે 5/6 બને, તો તે અપૂર્ણાંક શોધો.


( 6 ) પાંચ વર્ષ પછી જેકબની ઉંમર (વર્ષમાં) તેના પુત્રની ઉંમર (વર્ષમાં) કરતાં ત્રણ ગણી હશે. પાંચ વર્ષ પહેલા, જેકબની ઉંમર (વર્ષમાં) તેના પુત્રની ઉંમરથી સાત ગણી હોય, તો તેમની વર્તમાન ઉંમર શોધો.
ધારો કે, જેકબની વર્તમાન ઉંમર x વર્ષ અને તેના પુત્રની વર્તમાન ઉંમર y વર્ષ છે.
પાંચ વર્ષ બાદ, જેકબની ઉંમર (x + 5) વર્ષ અને તેના પુત્રની ઉંમર (y + 5) વર્ષ થશે.
આથી આપેલ માહિતી મુજબ,
(x + 5) = 3 (y + 5)
∴ x + 5 = 3y + 15
∴ x – 3y = 10

∴ 4y = 40
∴ y = 10
x = 7y – 30માં y = 10 મૂકતાં,
x = 7 (10) − 30
∴ x = 40
આમ, જેકબની અને તેના પુત્રની વર્તમાન ઉંમર અનુક્રમે 40 વર્ષ અને 10 વર્ષ છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. નીચેના સુરેખ સમીકરણયુગ્મના ઉકેલ આદેશની રીતે શોધો :


2. નીચેના સુરેખ સમીકરણયુગ્મના ઉકેલનું અસ્તિત્વ હોય તો આદેશની રીતે શોધો :

2 (7 – 2y) + 4y = 15
∴ 14 – 4y + 4y = 15
∴ 14 = 15
આમ, આપણને હંમેશાં ખોટું હોય તેવું વિધાન 14 = 15 મળે છે. આથી આપેલ સુરેખ સમીકરણયુગ્મના ઉકેલનું અસ્તિત્વ નથી.
3. બે સંખ્યાઓનો તફાવત 3 છે અને નાની સંખ્યાના ત્રણ ગણા અને મોટી સંખ્યાના બે ગણાનો સરવાળો 66 છે. તે બે સંખ્યાઓ શોધો.

∴ x = 15
આમ, માગેલ સંખ્યાઓ 15 અને 12 છે.
4. એક પેટીમાં ₹ 5ના તથા ₹ 2ના સિક્કા છે. કુલ સિક્કાની સંખ્યા 40 છે તથા કુલ રકમ ₹ 125 છે. દરેક પ્રકારના સિક્કાની સંખ્યા શોધો.
ધારો કે, પેટીમાં ₹ 5ના x સિક્કા અને ₹ 2ના y સિક્કા છે.
આથી આપેલ માહિતી મુજબ નીચે પ્રમાણેના બે સમીકરણ મળે :
x + y = 40 ……….. (1)
5x + 2y = 125 ………..(2)
સમીકરણ (1)માંથી x = 40 – y મળે.
સમીકરણ (2)માં x = 40 – y મૂકતાં,
5 (40 – y) + 2y = 125
∴ 200 – 5y + 2y = 125
∴ – 3y = − 75
∴ y = 25
x = 40 – પુમાં y = 25 મૂકતાં,
x = 40 – 25
∴ x = 15
આમ, પેટીમાં ર્ 5ના અને ર્ 2ના સિક્કાની સંખ્યા અનુક્રમે 15 અને 25 છે.
સ્વાધ્યાય – 3.4
1. નીચેનાં સુરેખ સમીકરણયુગ્મનો ઉકેલ લોપની રીતે અને આદેશની રીતે શોધો :



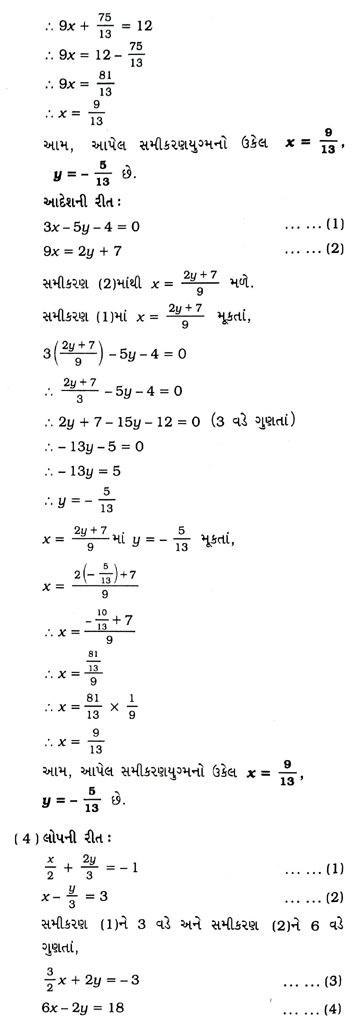

2. આપેલી સમસ્યાઓ પરથી સુરેખ સમીકરણયુગ્મ બનાવો અને તેમના ઉકેલો (જો શક્ય હોય તો) લોપની રીતે શોધો :
( 1 ) એક અપૂર્ણાંકના અંશમાં 1 ઉમેરતાં અને છેદમાંથી 1 બાદ કરતાં અપૂર્ણાંક કિંમત અતિસંક્ષિપ્ત રૂપમાં 1 બને છે. જો માત્ર છેદમાં 1 ઉમેરતાં અપૂર્ણાંકનું અતિસંક્ષિપ્ત સ્વરૂપ 1/2 બને, તો તે અપૂર્ણાંક શોધો.
ધારો કે, માગેલ અપૂર્ણાંકનો અંશ x અને છેદ y છે. આથી માગેલ અપૂર્ણાંક = x/y
પ્રશ્નમાં આપેલ પ્રથમ શરત મુજબ,

( 2 ) પાંચ વર્ષ પહેલા, નૂરીની ઉંમર સોનુની ઉંમરથી ત્રણ ગણી હતી. દસ વર્ષ પછી નૂરીની ઉંમર સોનુની ઉંમરથી બે ગણી થશે, તો નૂરી અને સોનુની વર્તમાન ઉંમર કેટલી થશે?
ધારો કે, નૂરીની વર્તમાન ઉંમર x વર્ષ અને સોનુની વર્તમાન ઉંમર y વર્ષ છે.
આથી પાંચ વર્ષ પહેલાં, નૂરીની ઉંમર (x – 5) વર્ષ અને સોનાની ઉંમર (y – 5) વર્ષ હતી.
તો, પ્રથમ શરત મુજબ,
(x – 5) = 3 (y – 5)
∴ x – 5 = 3y – 15
∴ x – 3y = – 10 ……… (1)
તે જ રીતે, દસ વર્ષ પછી, નૂરીની ઉંમર (x + 10) વર્ષ અને સોનુની ઉંમર (y + 10) વર્ષ થશે.
તો, દ્વિતીય શરત મુજબ,
x + 10 = 2 (y + 10)
∴ x + 10 = 2y + 20
∴ x – 2y = 10 ……… (2)
સમીકરણ (2)માંથી સમીકરણ (1) બાદ કરતાં,
(x – 2y) – (x – 3y) = 10 – ( – 10)
∴ x – 2y − x + 3y = 10 + 10
∴ y = 20
સમીકરણ (2)માં y = 20 મૂકતાં,
x – 2 (20) = 10
∴ x – 40 = 10
∴ x = 50
આમ, માહિતી પરથી મળતું સુરેખ સમીકરણયુગ્મ x – 3y = – 10 અને x − 2y = 10 છે તથા નૂરી અને સોનુની વર્તમાન ઉંમર અનુક્રમે 50 વર્ષ અને 20 વર્ષ છે.
(૩) બે અંકોની સંખ્યાના અંકોનો સરવાળો 9 છે. વળી સંખ્યાના નવ ગણા કરતાં મળતી સંખ્યા એ અંકોની અદલાબદલી કરતાં મળતી સંખ્યા કરતાં બે ગણી છે, તો તે સંખ્યા શોધો. ધારો કે, મૂળ સંખ્યામાં દશનો અંક x અને એકમનો અંક y છે.
આથી મૂળ સંખ્યા = 10x + y
તો, પ્રથમ શરત મુજબ,
x + y = 9 …….. (1)
અંકોની અદલાબદલી કરતાં મળતી સંખ્યામાં દશકનો અંક y અને એકમનો અંક x થાય.
આથી નવી સંખ્યા = 10y + x.
તો, દ્વિતીય શરત મુજબ,
9 (10x + y) = 2 ( 10y + x)
∴ 90x + 9y = 20y + 2x
∴ 88x – 1 1y = 0
∴ 8x – y = 0 (11 વડે ભાગતાં) ……… (2)
સમીકરણો (1) અને (2)નો સરવાળો લેતાં,
(x + y) + (8x – y) = 9 + 0
∴ 9x = 9
∴ x = 1
સમીકરણ (1)માં x = 1 મૂકતાં,
1 + y = 9
∴ y = 8
આથી મૂળ સંખ્યા = 10x + y
= 10 (1) + 8 = 18
આમ, માહિતી પરથી મળતું સુરેખ સમીકરણયુગ્મ x + y = 9 અને 8x – y = 0 છે તથા માગેલ સંખ્યા 18 છે.
( 4 ) મીના ₹ 2000 ઉપાડવા બૅન્કમાં ગઈ હતી. તેણે કૅશિયરને કહ્યું હતું કે મને માત્ર ₹ 50 અને ₹ 100ની નોટો જ જોઈએ છે. મીનાને કુલ 25 નોટો મળી હતી, તો તેણે ₹ 50 અને ₹ 100ની પ્રત્યેકની કેટલી કેટલી નોટો મેળવી હશે?
ધારો કે, મીનાને ર્ 50ની x નોટો અને ₹ 100ની y નોટો મળી હોય.
આથી તેને મળેલ કુલ ૨કમ = ₹ (50x + 100y) પરંતુ, પ્રથમ શરત મુજબ તેને કુલ ₹ 2000 મળેલ છે.
50x + 100y = 2000
∴ x + 2y = 40 (50 વડે ભાગતાં) …….. (1)
દ્વિતીય શરત મુજબ તેને કુલ 25 નોટો મળી છે.
∴ x + y = 25 ……… (2)
સમીકરણ (1)માંથી સમીકરણ (2) બાદ કરતાં,
(x + 2y) – (x + y) = 40 – 25
∴ y = 15
સમીકરણ (2)માં y = 15 મૂકતાં,
x + 15 = 25
∴ x = 10
આમ, માહિતી ૫૨થી મળતું સુરેખ સમીકરણયુગ્મ x + 2y = 40 અને x + y = 25 છે તથા મીનાએ ₹ 50ની 10 નોટો તથા ₹ 100ની 15 નોટો મેળવી હશે.
( 5 ) એક પ્રતિષ્ઠિત પુસ્તકાલય પ્રથમ ત્રણ દિવસનું એક પુસ્તકનું નિશ્ચિત ભાડું લે છે અને પછીના પ્રત્યેક દિવસદીઠ અતિરિક્ત ભાડું લે છે. સિરતા સાત દિવસ પુસ્તક રાખવાના ₹ 27 ચૂવે છે. સુસી પાંચ દિવસ પુસ્તક રાખવાના ₹ 21 ચૂકવે છે, તો નિશ્ચિત ભાડું અને પ્રત્યેક વધારાના દિવસનું ભાડું શોધો.
ધારો કે, પ્રથમ ત્રણ દિવસનું નિશ્ચિત ભાડું ₹ x અને પ્રથમ ત્રણ દિવસ પછીના વધારાના દિવસો માટે દિવસ- દીઠ ભાડું ₹ y છે.
સરિતા 7 દિવસ પુસ્તક રાખે છે.
આથી સરિતાને 4 દિવસ (7 – 3) માટેનું વધારાનું ભાડું ચૂકવવું પડે. આથી આપણને સરિતા માટે નીચેનું સમીકરણ મળે :
x + 4y = 27 ……. (1)
સુસી 5 દિવસ પુસ્તક રાખે છે. આથી સુસીને 2 દિવસ (5 – 3) માટેનું વધારાનું ભાડું ચૂકવવું પડે. આથી આપણને સુસી માટે નીચેનું સમીકરણ મળે :
x + 2y = 21 …….. (2)
સમીકરણ (1)માંથી સમીકરણ (2) બાદ કરતાં,
(x + 4y) – (x + 2y) = 27 – 21
∴ 2y = 6
∴ y = 3
સમીકરણ (1)માં y = 3 મૂકતાં,
x + 4 (3) = 27
∴ x + 12 = 27
∴ x = 15
આમ, માહિતી પરથી મળતું સુરેખ સમીકરણયુગ્મ x + 4y = 27 અને x + 2y = 21 છે તથા પ્રથમ ત્રણ દિવસનું નિશ્ચિત ભાડું ₹ 15 અને પ્રત્યેક વધારાના દિવસનું ભાડું ₹ 3 છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. લોપની રીતે નીચેના સમીકરણયુગ્મનો ઉકેલ શોધો :

2. લોપની રીતે નીચેના સમીકરણયુગ્મનો ઉકેલ શોધો :


3. કાવ્યા તેની કુલ બચત ₹ 40,000નું રોકાણ બે ભાગમાં કરે છે. તે અમુક રકમ 6 % વ્યાજના દરે અને બાકીની રકમ 8% વ્યાજના દરે રોકે છે. જો તેને એક વર્ષનું કુલ વ્યાજ ₹ 3000 મળે, તો તેણે દરેક વ્યાજના દરે રોકેલ રકમ શોધો.
ધારો કે, કાવ્યા 6 % વ્યાજના દરે ₹ x અને 8% વ્યાજના દ૨ે ₹ yનું રોકાણ કરે છે.

સ્વાધ્યાય – 3.5
1. નીચેના પૈકી ક્યા સુરેખ સમીકરણયુગ્મને અનન્ય ઉકેલ નથી અથવા અનંત ઉકેલો છે, તે જણાવો. જો અનન્ય ઉકેલ હોય, તો ચોકડી ગુણાકારની રીતે તેનો ઉકેલ શોધો.



2. ( 1 ) નીચેના સુરેખ સમીકરણયુગ્મને a અને bની કઈ કિંમતો માટે અનંત ઉકેલો છે?


3. નીચેના સુરેખ સમીકરણયુગ્મનો ઉકેલ આદેશની રીતે અને ચોકડી ગુણાકારની રીતે શોધો :


4. નીચેના કૂટપ્રશ્નોમાં સુરેખ સમીકરણયુગ્મ મેળવો અને કોઈ પણ બૈજિક રીતે તેમના ઉકેલ (જો શક્ય હોય તો) શોધો :
( 1 ) એક હોસ્ટેલના વિદ્યાર્થીઓનું ભોજન-ખર્ચ અંશતઃ અચળ અને અંશતઃ વિદ્યાર્થીઓએ જેટલા દિવસ ભોજન લીધું હોય તે દિવસોની સંખ્યાના પ્રમાણમાં હોય છે. વિદ્યાર્થી A, 20 દિવસ ભોજન લે છે અને તેનું ભોજન-ખર્ચ ₹ 1000 ચૂકવે છે. વિદ્યાર્થી B, 26 દિવસ ભોજન લે છે અને ભોજન-ખર્ચ પેટે ₹ 1180 ચૂકવે છે, તો નિશ્ચિત ખર્ચ તથા દૈનિક ભોજન-ખર્ચ શોધો.
ધારો કે, નિશ્ચિત માસિક દર ₹ x અને દૈનિક ભોજન- ખર્ચ ₹ y છે.
તો, આપેલ માહિતી પરથી નીચે મુજબના બે સુરેખ સમીકરણો મળે :

આમ, નિશ્ચિત માસિક દર ₹ 400 અને દૈનિક ભોજન- ખર્ચ ₹ 30 છે.
નોંધ : અહીં, લોપની રીત ખૂબ જ સહેલી પડે તેમ છે, પરંતુ ચોકડી ગુણાકારની રીતનો વધુ ઉપયોગ શિખાય તે માટે ચોકડી ગુણાકારની રીત બતાવી છે.
( 2 ) એક અપૂર્ણાંકના અંશમાંથી 1 બાદ કરવામાં આવે તો નવા અપૂર્ણાંકનું અતિસંક્ષિપ્ત સ્વરૂપ 1/3 છે અને તે જ અપૂર્ણાંકના છેદમાં 8 ઉમેરવામાં આવે, તો મળતા અપૂર્ણાંકનું અતિસંક્ષિપ્ત સ્વરૂપ 1/4 થાય છે, તો તે અપૂર્ણાંક શોધો.


( 3 ) યશને એક કસોટીમાં 40 ગુણ મળ્યા હતા. તેને પ્રત્યેક સાચા જવાબના 3 ગુણ મળે છે અને પ્રત્યેક ખોટા જવાબ માટે 1 ગુણ કપાય છે. જો પરીક્ષકે દરેક સત્ય જવાબ માટે 4 ગુણ આપ્યા હોત અને દરેક ખોટા જવાબ માટે 2 ગુણ કાપ્યા હોત, તો યશે 50 ગુણ મેળવ્યા હોત. તો આ કસોટીમાં કેટલા પ્રશ્નો હતા?
ધારો કે, યશે આપેલ જવાબોમાં x જવાબ સાચા અને y જવાબ ખોટા છે.
તો, આપેલ માહિતી પરથી નીચેના સમીકરણો મળે :

( 4 ) ધોરીમાર્ગ પર સ્થાન A અને સ્થાન B એકબીજાથી 100 કિમી દૂર છે. એક ગાડી Aથી ઊપડે છે અને બીજી ગાડી Bથી ઊપડે છે. ગાડીઓ એક જ દિશામાં ભિન્ન પરંતુ એકધારી ઝડપથી ચાલે તો 5 કલાકમાં એકબીજાને મળે છે. તેઓ એકબીજા તરફ ચાલે તો તે 1 કલાકમાં મળે છે, તો બે ગાડીઓની ઝડપ કેટલી હશે?
ધારો કે, સ્થાન Aથી ઊપડતી ગાડીની ઝડપ x કિમી / કલાક અને સ્થાન Bથી ઊપડતી ગાડીની ઝડપ yકિમી / કલાક છે, જ્યાં x > y. જો ગાડીઓ એક જ દિશામાં ચાલતી હોય તો તે બંને Aથી B તરફની દિશામાં ગતિ કરતી હોય, કારણ કે Aથી ઊપડતી ગાડીની ઝડપ Bથી ઊપડતી ગાડીની ઝડપ કરતાં વધુ છે.

આમ, સ્થાન A પરથી ઊપડતી ગાડીની ઝડપ સ્થાન B પરથી ઊપડતી ગાડીની ઝડપ કરતાં વધુ છે તે ધારણા મુજબ સ્થાન Aથી ઊપડતી ગાડીની ઝડપ 60 કિમી / કલાક અને સ્થાન Bથી ઊપડતી ગાડીની ઝડપ 40 કિમી / કલાક છે.
( 5 ) જો એક લંબચોરસની લંબાઈમાં 5 એકમ ઘટાડો થાય અને પહોળાઈમાં 3 એકમ વધારો થાય, તો લંબચોરસનું ક્ષેત્રફળ 9 ચોરસ એકમ જેટલું ઘટે છે. જો આપણે લંબાઈમાં 3 એકમ અને પહોળાઈમાં 2 એકમ વધારીએ, તો ક્ષેત્રફળ 67 ચોરસ એકમ વધે છે, તો લંબચોરસનાં પરિમાણ શોધો.
ધારો કે, લંબચોરસની લંબાઈ x એકમ અને પહોળાઈ y એકમ છે.
લંબચોરસનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
∴ આપેલ લંબચોરસનું ક્ષેત્રફળ = xy ચોરસ એકમ
પ્રથમ શરત મુજબ, ઘટાડેલ લંબાઈ = (x – 5) એકમ,
વધારેલ પહોળાઈ = ( y + 3) એકમ થાય અને
ક્ષેત્રફળ = (xy – 9) ચોરસ એકમ થાય.
હવે, લંબાઈ × પહોળાઈ = લંબચોરસનું ક્ષેત્રફળ
∴ (x – 5) (y + 3) = xy – 9
∴ xy + 3x – 5y – 15 = xy – 9
∴ 3x – 5y – 6 = 0 …….. (1)
તે જ રીતે, દ્વિતીય શરત મુજબ, વધારેલ લંબાઈ = (x + 3) એકમ, વધારેલ પહોળાઈ = (y + 2) એકમ અને ક્ષેત્રફળ = (xy + 67) ચોરસ એકમ થાય.
હવે, લંબાઈ × પહોળાઈ = લંબચોરસનું ક્ષેત્રફળ
∴ (x + 3) (y + 2) = xy + 67
∴ xy + 2x + 3y + 6 = xy + 67
∴ 2x + 3y – 61 = 0 ……… (2)
સમીકરણયુગ્મનો ઉકેલ આપણે ચોકડી ગુણાકારની રીતે મેળવીએ.
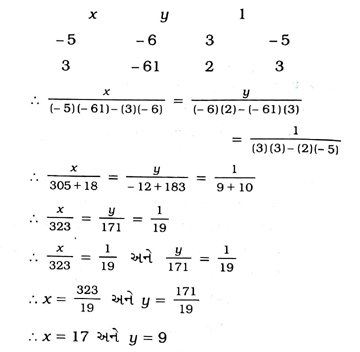
આમ, આપેલ લંબચોરસની લંબાઈ અને પહોળાઈ અનુક્રમે 17 એકમ અને 9 એકમ છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. નીચેના સુરેખ સમીકરણયુગ્મોના ઉકેલ ચોકડી ગુણાકારની રીતે શોધો :


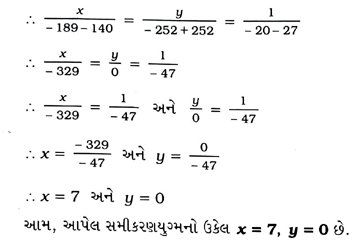
2. kની કઈ કિંમતો માટે સુરેખ સમીકરણયુગ્મ kx + y = k2 અને x + ky = 1 માટે ( 1 ) ઉકેલ ન મળે? ( 2 ) અસંખ્ય ઉકેલ મળે? (૩) અનન્ય ઉકેલ મળે?
બંને સમીકરણને પ્રમાણિત સ્વરૂપમાં દર્શાવતાં,
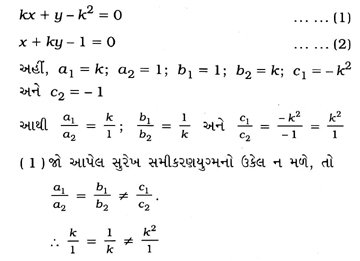

આમ, k ≠ ± 1, એટલે કે, ± 1 સિવાયની કોઈ વાસ્તવિક સંખ્યા k માટે આપેલ સમીકરણયુગ્મનો અનન્ય ઉકેલ મળે.
સ્વાધ્યાય 3.6
1. નીચેના સમીકરણયુગ્મને યોગ્ય આદેશ વડે સુરેખ સમીકરણયુગ્મમાં રૂપાંતરિત કરીને તેમનો ઉકેલ મેળવો :






2. નીચેની સમસ્યાઓમાંથી સમીકરણયુગ્મ રચો અને તેમનો ઉકેલ શોધો :
( 1 ) રીતુ પ્રવાહની દિશામાં 20 કિમી અંતર 2 કલાકમાં અને પ્રવાહની સામેની દિશામાં 4 કિમી અંતર 2 કલાકમાં કાપે છે. તેની સ્થિર પાણીમાં ઝડપ અને પ્રવાહની ઝડપ શોધો.
ધારો કે, રીતુની સ્થિર પાણીમાં ઝડપ x કિમી/કલાક છે અને પ્રવાહની ઝડપ y કિમી/કલાક છે.
આથી પ્રવાહની દિશામાં રીતુની ઝડપ (x + y) કિમી / કલાક થાય અને પ્રવાહની સામેની દિશામાં રીતુની ઝડપ (x – y) કિમી / કલાક થાય.

(2) 2 સ્ત્રીઓ અને 5 પુરુષો સાથે મળીને એક ભરતકામ 4 દિવસમાં પૂરું કરી શકે છે. જો 3 સ્ત્રીઓ અને 6 પુરુષોને તે જ કામ સોંપવામાં આવે, તો તે કામ 3 દિવસમાં પૂરું કરે છે. તો એક સ્ત્રીને સ્વતંત્ર રીતે કામ પૂરું કરતાં કેટલો સમય લાગે? એક પુરુષને સ્વતંત્ર રીતે કામ પૂરું કરતાં કેટલો સમય લાગે?
ધારો કે, એક સ્ત્રીને સ્વતંત્ર રીતે કામ પૂરું કરતાં x દિવસ લાગે અને એક પુરુષને સ્વતંત્ર રીતે કામ પૂરું કરતાં y દિવસ લાગે છે.

આમ, એક સ્ત્રીને સ્વતંત્ર રીતે કામ પૂરું કરતાં 18 દિવસ લાગે અને એક પુરુષને સ્વતંત્ર રીતે કામ પૂરું કરતાં 36 દિવસ લાગે.
(3) રૂહી તેના વતન જવા માટે 300 કિમીની મુસાફરી અંશતઃ ટ્રેન દ્વારા અને અંશતઃ બસ દ્વારા કરે છે. જો તે 60 કિમી મુસાફરી ટ્રેન દ્વારા અને બાકીની મુસાફરી બસ દ્વારા કરે, તો તેને વતન પહોંચતા 4 કલાક લાગે છે. જો તે ટ્રેન દ્વારા 100 કિમી અને બાકીની મુસાફરી બસ દ્વારા કરે, તો તેને વતન પહોંચતા 10 મિનિટ વધારે લાગે છે, તો ટ્રેન અને બસની પ્રતિકલાક સરેરાશ ઝડપ શોધો.
ધારો કે, ટ્રેનની સરેરાશ ઝડપ x કિમી / કલાક અને બસની સરેરાશ ઝડપ y કિમી / કલાક છે.


મહત્ત્વનાં અન્ય ઉદાહ૨ણો
1. x અને y શોધો : (કોઈ પણ છેદ શૂન્ય નથી.)


2. નીચેના સમીકરણયુગ્મનો ઉકેલ શોધો :

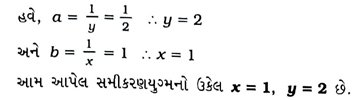
3. એક હોડી નદીના સામા પ્રવાહે 32 કિમી અને પ્રવાહની દિશામાં 36 કિમી અંતર 7 કલાકમાં કાપે છે. તે હોડીને તે જ નદીમાં સામા પ્રવાહે 40 કિમી અને પ્રવાહની દિશામાં 48 કિમી અંતર કાપતાં 9 કલાક લાગે છે. હોડીની સ્થિર પાણીમાં ઝડપ અને નદીના પ્રવાહની ઝડપ શોધો.
ધારો કે, હોડીની સ્થિર પાણીમાં ઝડપ x કિમી / કલાક છે અને નદીના પ્રવાહની ઝડપ yકિમી / કલાક છે.
આથી પ્રવાહની દિશામાં હોડીની ઝડપ (x + y) કિમી / કલાક થાય અને પ્રવાહની સામેની દિશામાં હોડીની ઝડપ (x – y) કિમી / કલાક થાય.
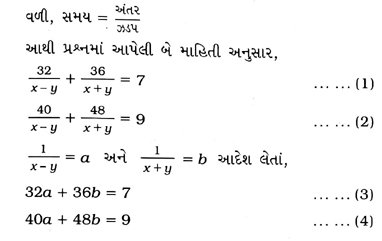

સ્વાધ્યાય – 3.7
આ સ્વાધ્યાય પરીક્ષા માટે ધ્યાનમાં લેવાનું નથી.
1. બે મિત્રો અની અને બીજુની ઉંમરનો તફાવત 3 વર્ષ છે. અનીના પિતા ધરમની ઉંમર (વર્ષમાં) અનીની ઉંમરથી બમણી અને બીજુની ઉંમર (વર્ષમાં) તેની બહેન કેથી કરતાં બે ગણી છે. જો કેથી અને ધરમની ઉંમરના વર્ષનો તફાવત 30 વર્ષનો હોય, તો અની અને બીજુની ઉંમર શોધો.
ધારો કે, અનીની ઉંમર x વર્ષ અને બીજુની ઉંમર y વર્ષ છે. તો, આપેલ માહિતી મુજબ
x – y = 3 ……. (1)
અથવા y − x = 3 …….. (2)
ધરમની ઉંમર અનીની ઉંમર કરતાં બમણી છે.
∴ ધરમની ઉંમર = 2x વર્ષ
બીજુની ઉંમર તેની બહેન કેથીની ઉંમરથી બે ગણી છે. એટલે કે કેથીની ઉંમર બીજુની ઉંમર કરતાં અડધી છે.
∴કેથીની ઉંમર = y/2 વર્ષ
સ્વાભાવિક છે કે ધરમની ઉંમર કેથીની ઉંમર કરતાં વધારે છે.
∴ 2x – y/2 = 30
∴ 4x – y = 60 …….. (3)
( 1 )પ્રથમ આપણે સમીકરણ (1) અને સમીકરણ (3)નો ઉકેલ શોધીએ.
સમીકરણ (3)માંથી સમીકરણ (1) બાદ કરતાં,
(4x – y) – (x – y) = 60 – 3
∴ 3x = 57
∴ x = 19
સમીકરણ (1)માં x = 19 મૂકતાં,
19 – y = 3
∴ 19 – 3 = y
∴ y = 16
આમ, અન્નીની ઉંમર 19 વર્ષ અને બીજુની ઉંમર 16 વર્ષ થાય.
( 2 ) હવે આપણે સમીકરણ (2) અને સમીકરણ (3)નો ઉકેલ શોધીએ.
સમીકરણો (2) અને (3)નો સરવાળો લેતાં,
(y − x) + (4x – y) = 3 + 60
∴ 3x = 63
∴ x = 21
સમીકરણ (2)માં x = 21 મૂકતાં,
y – 21 = 3
∴ y = 24
આમ, અનીની ઉંમર 21 વર્ષ અને બીજુની ઉંમર 24 વર્ષ થાય.
આથી અની અને બીજુની ઉંમર અનુક્રમે 19 વર્ષ અને 16 વર્ષ અથવા 21 વર્ષ અને 24 વર્ષ છે.
2. એક વ્યક્તિ તેના મિત્રને કહે છે, “જો તું મને સો રૂપિયા આપે, તો મારી પાસે તારાથી બે ગણા રૂપિયા હશે.” બીજો વ્યક્તિ કહે છે, “જો તું મને દસ રૂપિયા આપે, તો મારી પાસે તારાથી છ ગણા રૂપિયા હશે.” અનુક્રમે બંનેની મૂડી ૨કમ જણાવો. [ભાસ્કર IIના બીજગણિતમાંથી]
[સૂચન: x + 100 = 2 (y – 100), y + 10 = 6 (x – 10)] ધારો કે, પ્રથમ વ્યક્તિ (જેને આપણે A કહીએ) પાસે ₹ x અને બીજી વ્યક્તિ (જેને આપણે B કહીએ) પાસે ₹ y છે.
જો Bએ Aને ₹ 100 આપે, તો A પાસે ₹ (x + 100) થાય અને B પાસે ₹ (y – 100) થાય.
આપેલ શરત મુજબ,
x + 100 = 2 (y – 100)
∴ x + 100 = 2y – 200
∴ x – 2y = – 300 ……. (1)
જો A એ Bને ₹ 10 આપે, તો A પાસે ₹ (x – 10) થાય અને B પાસે ₹ (y + 10) થાય.
આપેલ શરત મુજબ,
y + 10 = 6 (x – 10)
∴ y + 10 = 6x – 60
∴ 10 + 60 = 6x – y
∴ 6x – y = 70 …….. (2)
સમીકરણ (2)ને 2 વડે ગુણતાં,
12x – 2y = 140 …….. (3)
સમીકરણ (3)માંથી સમીકરણ (1) બાદ કરતાં,
(12x – 2y) – (x – 2y) = 140 − (– 300)
∴ 11x = 440
∴ x = 40
સમીકરણ (1)માં x = 40 મૂકતાં,
40 – 2y = – 300
∴ 40 + 300 = 2y
∴ 2y = 340
∴ y = 170
આમ, પ્રથમ વ્યક્તિ પાસે ₹ 40 છે અને બીજા વ્યક્તિ પાસે ₹ 170 છે.
3. એક ટ્રેન અચળ ઝડપે ચોક્કસ અંતર કાપે છે. જો ટ્રેનની ઝડપમાં 10 કિમી / કલાક વધારો થાય, તો તે મુસાફરી માટે નક્કી સમય કરતાં 2 કલાક ઓછો સમય લે છે અને ટ્રેનની ઝડપમાં 10 કિમી/કલાકનો ઘટાડો કરતાં, તે મુસાફરી માટે નક્કી સમય કરતાં 3 કલાક વધારે સમય લે છે, તો ટ્રેન દ્વારા કપાયેલું કુલ અંતર શોધો.
ધારો કે, ટ્રેનની કાયમી અચળ ઝડપ x કિમી/કલાક છે અને મુસાફરીનો કાયમી સમય y ક્લાક છે. આથી ટ્રેન દ્વારા કપાયેલું કુલ અંતર = ઝડપ × સમય = xy કિમી.
હવે, પ્રથમ માહિતી મુજબ, ટ્રેનની નવી ઝડપ = (x + 10) કિમી / કલાક અને નવો સમય = (y – 2) કલાક.
વળી, ઝડપ X સમય = અંતર પરથી
(x + 10) (y – 2) = xy
∴ xy – 2x + 10y – 20 = xy
∴ – 2x + 10y = 20 ……. (1)
તે જ રીતે, દ્વિતીય માહિતી મુજબ, ટ્રેનની નવી ઝડપ = (x – 10) કિમી / કલાક અને નવો સમય = (y + 3) કલાક.
આથી (x – 10) (y + 3) = xy
∴ xy + 3x – 10y – 30 = xy
∴ 3x – 10y = 30 …….. (2)
સમીકરણો (1) અને (2)નો સરવાળો લેતાં,
(– 2x + 10y) + (3x – 10y) = 20 + 30
∴ x = 50
સમીકરણ (1)માં x = 50 મૂકતાં,
– 2 (50) + 10y = 20
∴ – 100 + 10y = 20
∴ 10y = 120
∴ y = 12
હવે, ટ્રેન દ્વારા કપાયેલું કુલ અંતર = xy = 50 × 12 = 600 કિમી
આમ, ટ્રેન દ્વારા કપાયેલું કુલ અંતર 600 કિમી છે.
4. એક વર્ગના વિદ્યાર્થીઓને હારમાં ઊભા રાખવામાં આવ્યા છે. દરેક હારમાં 3 વિદ્યાર્થીઓ વધારે ઊભા રાખતાં 1 હાર ઓછી બને છે. ૩ વિદ્યાર્થીઓ પ્રત્યેક હારમાં ઓછા ઊભા રાખતાં 2 હાર વધારે બને છે, તો વર્ગખંડમાં રહેલા વિદ્યાર્થીઓની સંખ્યા શોધો.
ધારો કે, દરેક હારમાં ઊભા રાખેલ વિદ્યાર્થીઓની સંખ્યા x છે અને કુલ હારની સંખ્યા y છે. આથી કુલ વિદ્યાર્થીઓની સંખ્યા = xy થાય.
હવે, પ્રથમ માહિતી મુજબ, દરેક હારમાં ઊભા રાખેલ વિદ્યાર્થીઓની સંખ્યા = (x + 3) અને કુલ હારની સંખ્યા = y − 1 થાય.
∴ (x + 3) (y – 1) = xy
∴ xy − x + 3y – 3 = xy
∴ − x + 3y = 3 …….. (1)
તે જ રીતે, દ્વિતીય માહિતી મુજબ, દરેક હારમાં ઊભા રાખેલ વિદ્યાર્થીઓની સંખ્યા = = (x – 3) અને કુલ હારની સંખ્યા = (y + 2) થાય.
∴ (x – 3) (y + 2) = xy
∴ xy + 2x – 3y – 6 = xy
∴ 2x – 3y = 6 ……. (2)
સમીકરણો (1) અને (2)નો સરવાળો લેતાં,
(− x + 3y) + (2x – 3y) = 3 + 6
∴ x = 9
સમીકરણ (1)માં x = 9 મૂકતાં,
– 9 + 3y = 3
∴ 3y = 12
∴ y = 4
હવે, કુલ વિદ્યાર્થીઓની સંખ્યા = xy = 9 × 4 = 36.
આમ, વર્ગખંડમાં રહેલા વિદ્યાર્થીઓની સંખ્યા 36 છે.
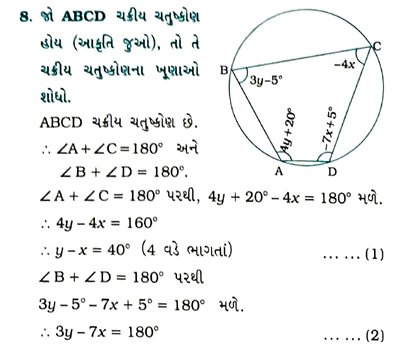
5. ΔABCમાં C = 3∠ B = 2 (∠A+∠B) હોય, તો ત્રિકોણના ત્રણેય ખૂણાઓનાં માપ શોધો.

6. સમીકરણો 5x – y = 5 અને 3x – y = 3 દ્વારા દર્શાવાતી રેખાના આલેખ દોરો. પુ-અક્ષ અને બંને રેખાઓ દ્વારા બનતા ત્રિકોણનાં શિરોબિંદુઓ જણાવો.

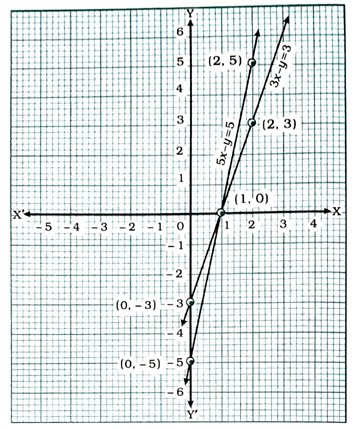
આલેખમાંથી સ્પષ્ટ છે કે પુ-અક્ષ અને બંને સમીકરણોની રેખાઓ દ્વારા બનતા ત્રિકોણના શિરોબિંદુઓ (1, 0), (0, − 3) અને (0, − 5) છે.
7. નીચેનાં સુરેખ સમીકરણયુગ્મ ઉકેલો :




હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
( 1 ) જો x = 2, y = 3 એ સુરેખ સમીકરણ 5x – 3y = kનો એક ઉકેલ હોય, તો k = ………
( 2 ) જલ્પાના દીકરા આહાનની વર્તમાન ઉંમર જલ્પાની વર્તમાન ઉંમર કરતાં ત્રીજા ભાગની છે. જો જલ્પાની વર્તમાન ઉંમર x વર્ષ હોય, તો 12 વર્ષ બાદ આહાનની ઉંમર …….. વર્ષ થશે.
( 3 ) x-અક્ષ, y-અક્ષ અને રેખા x + y = 6 દ્વારા બનતા ત્રિકોણનું ક્ષેત્રફળ ……… ચોરસ એકમ થાય.
( 4 ) બે સંખ્યાઓનો સરવાળો 30 છે તથા તેમનો તફાવત 16 છે. તે સંખ્યાઓ પૈકીની નાની સંખ્યા ……… છે.
( 5 ) જો y = x/2 અને 3x + 4y = 20 હોય, તો x = ………
( 6 ) જો 13x + 19y = 90 અને 19x + 13y = 70 હોય, તો x + y = ……..
( 7 ) પિતાની હાલની ઉંમર x વર્ષ અને તેમના બે પુત્રની હાલની ઉંમરનો સરવાળો ૫ વર્ષ છે, તો તેમની 5 વર્ષ પછીની ઉંમરનો સરવાળો …….. વર્ષ થશે.
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :

(10) સમીકરણયુગ્મ 4x + 3y = 14 અને ……… ના આલેખ સમાંતર રેખાઓ છે.
A. 3x + 4y = 14
B. 8x + 6y = 28
C. 12x + 9y = 42
D. – 12x = 9y
3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ આપો :

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here