Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 11 Constructions (રચના)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 11 Constructions (રચના)
સ્વાધ્યાય – 11.1
- નીચેના પૈકી પ્રત્યેકની રચના કરી, તેની રચનાના મુદ્દા તથા તેની યથાર્થતા આપો :
1. 7.6 સેમી લંબાઈનો રેખાખંડ દોરી, તેનું 5 : 8 ગુણોત્તરમાં વિભાજન કરો. બંને ભાગ માપો.
પક્ષ : 7.6 સેમી લંબાઈનો રેખાખંડ AB આપેલ છે.
કૃત્ય : ABનું 5 : 8 ગુણોત્તરમાં વિભાજન કરતું બિંદુ C મેળવવું તથા AC અને BC માપવા.
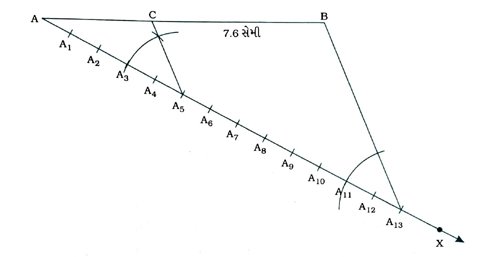
રચનાના મુદ્દા :
( 1 ) AB સાથે લઘુકોણ બનાવે તેવું કોઈ પણ કિરણ AX રચો.
( 2 ) AX પર AA1 = A1A2 = A2A3 = ….. = A12A13 થાય તેવાં 13 (5 + 8) બિંદુઓ A1, A2, A3, …, A13નાં સ્થાન નક્કી કરો.
( 3 ) BA13 જોડો.
( 4 ) બિંદુ A5માંથી A13Bને સમાંતર હોય તેવી રેખા દોરો, જે ABને C બિંદુમાં છેદે. આ માટે ∠AA13Bને સમાન હોય તેવો ∠AA5C રચો.
( 5 ) આ રીતે મળતું બિંદુ C એ ABનું 5: 8 ગુણોત્તરમાં વિભાજન કરતું બિંદુ છે. એટલે કે, AC : CB = 5 : 8.
ABના બે ભાગ માપતા આપણને AC = 2.9 સેમી અને BC = 4.7 સેમી મળે.
યથાર્થતા :

વૈકલ્પિક રીત :
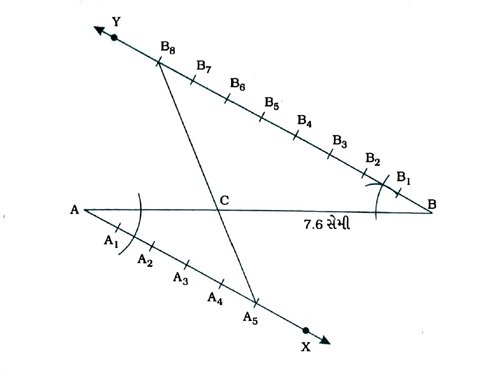
રચનાના મુદ્દા :
( 1 ) ABની સામસામેની (વિરુદ્ધ) બાજુઓમાં કિરણ AX અને BY એવાં દોરો કે, જેથી ∠BAX અને ∠ABY સમાન ખૂણા થાય. (સરળતા ખાતર ∠BAX = ∠ABY = 60° થાય તેવાં કિરણ AX અને BY દોરો.)
( 2 ) AX પર પાંચ બિંદુઓ A1, A2, A3, A4 તથા A5 અને BY પર આઠ બિંદુઓ B1, B2, B3, B4, B5, B6, B7, B8નાં સ્થાન એવાં નક્કી કરો, જેથી AA1 = A1A2 = A2A3 = A3A4 = A4A5 = BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7 = B7B8 થાય.
( 3 ) B8A5 દોરો જે ABને C બિંદુમાં છેદે.
( 4 ) આ રીતે મળતું બિંદુ C એ ABનું 5: 8 ગુણોત્તરમાં વિભાજન કરતું બિંદુ છે. એટલે કે, AC : CB = 5 : 8.
યથાર્થતા :

2. 4 સેમી, 5 સેમી અને 6 સેમી બાજુવાળા ત્રિકોણની રચના કરો અને પછી આ ત્રિકોણની બાજુઓને અનુરૂપ તે બાજુઓથી 2/3 ગણી બાજુવાળા ત્રિકોણની રચના કરો.
કૃત્ય : AB = 4 સેમી, BC = 6 સેમી અને AC = 5 સેમી હોય તેવો Δ ABC રચવો અને ત્યારબાદ A ABCને સમરૂપ હોય તેવો એક ત્રિકોણ રચવો, જેની અનુરૂપ બાજુઓનો ત્રિકોણ ABCની બાજુઓ સાથેનો ગુણોત્તર હોય.
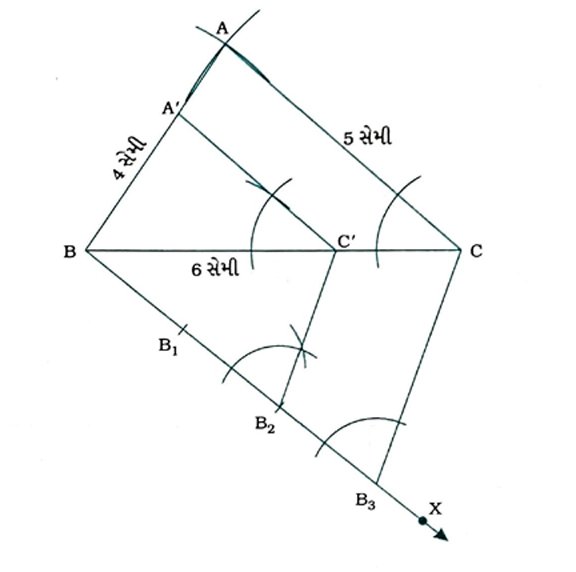
રચનાના મુદ્દા :
( 1 ) Δ ABC રચો, જેમાં AB = 4 સેમી, BC = 6 સેમી અને AC = 5 સેમી હોય.
( 2 ) BCના જે અર્ધતલમાં બિંદુ A હોય તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
( 3 ) BB1 = B1B2 = B2B3 થાય તેવાં ત્રણ બિંદુઓ B1, B2 અને B3 ને BX પર અંકિત કરો.
( 4 ) B3C જોડો.
( 5 ) B2 માંથી B3Cને સમાંતર રેખા દોરો, જે BCને Cમાં છેદે. આ માટે ∠BB3Cને સમાન હોય તેવો ∠BB2C’ રચો.
( 6 ) ∠BCAને સમાન ∠BC’A’ રચો જેથી કિરણ C’A’ એ BAને A’માં છેદે અને C’A’ || CA થાય.
આથી ΔA’BC’ એ માગેલ માપ મુજબનો ΔABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને Δ A’BC’ની બાજુઓ તથા Δ ABCની અનુરૂપ બાજુઓનો ગુણોત્તર 2/3 છે.
યથાર્થતા :

3. 5 સેમી, 6 સેમી અને 7 સેમી બાજુવાળા ત્રિકોણની રચના કરો અને પછી બીજો ત્રિકોણ રચો, જેની બાજુઓ પ્રથમ ત્રિકોણની અનુરૂપ બાજુઓ કરતાં 7/5 ગણી હોય.
નૃત્ય : AB = 5 સેમી, BC = 7 સેમી અને AC = 6 સેમી હોય તેવો Δ ABC રચવો અને ત્યારબાદ AABCને સમરૂપ હોય તેવો એક ત્રિકોણ રચવો, જેની અનુરૂપ બાજુઓનો Δ ABCની બાજુઓ સાથેનો ગુણોત્તર 7/5 હોય.
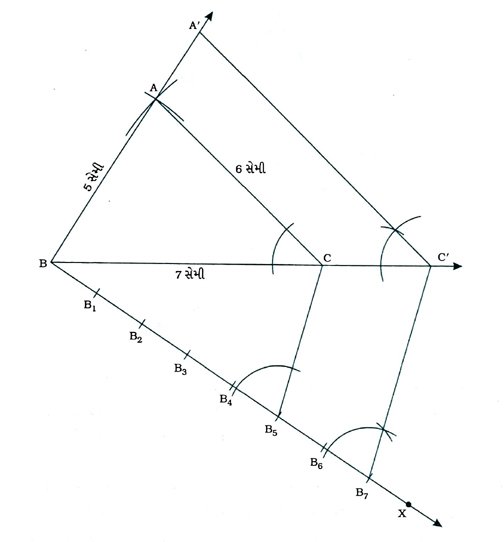
રચનાના મુદ્દા :
( 1 ) Δ ABC રચો, જેમાં AB = 5 સેમી, BC = 7 સેમી અને AC = 6 સેમી હોય.
( 2 ) BCના જે અર્ધતલમાં બિંદુ A હોય તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
( 3 ) BB1 = B1B2 = B2B3 = …… = B6B7 થાય તેવાં સાત બિંદુઓ B1, B2, B3, ……. B7 ને BX ૫૨ અંકિત કરો.
( 4 ) B5C જોડો.
( 5 ) ∠BB7C’ = ∠BB5C રચીને B7માંથી પસાર થતી અને B5Cને સમાંતર રેખા દોરો, જે લંબાવેલ BCને C’માં છેદે.
( 6 ) ∠BC’A’ = ∠BCA રચીને C’માંથી પસાર થતી અને CAને સમાંતર રેખા દોરો, જે લંબાવેલ BAને A’માં છેદે.
આથી Δ ABC’ એ માગેલ માપ મુજબનો Δ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને Δ ABCની બાજુઓ તથા A ABCની અનુરૂપ બાજુઓનો ગુણોત્તર 7/5 છે.
યથાર્થતા :
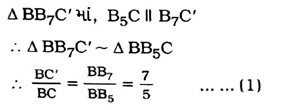

4. 8 સેમી આધાર અને 4 સેમી વેધવાળા સમદ્વિબાજુ ત્રિકોણની રચના કરો અને પછી બીજો એવો ત્રિકોણ રચો, જેની બાજુઓ સતિભુજ ત્રિકોણની અનુરૂપ બાજુઓ કરતાં 1½ ગણી હોય.
કૃત્ય : સમદ્વિબાજુ Δ ABC રચવો, જેમાં આધાર BC = 8 સેમી અને વેધ AD = 4 સેમી હોય. ત્યારબાદ Δ ABCને સમરૂપ હોય તેવો બીજો ત્રિકોણ રચવો, જેની બાજુઓ Δ ABCની અનુરૂપ બાજુઓ કરતાં 1½ ગણી હોય.

રચનાના મુદ્દા :
( 1 ) સમદ્વિબાજુ Δ ABC રચો, જેમાં પાયો BC = 8સેમી અને વેધ AD = 4 સેમી હોય.
( 2 ) BCના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્થતલમાં કિરણ BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
( 3 ) BB1 = B1B2 = B2B3 થાય તેવાં ત્રણ બિંદુઓ B1, B2 અને B3 ને BX પર અંકિત કરો.
( 4 ) B2C જોડો.
( 5 ) ∠BB3C’ = ∠BB2C રચીને B૰માંથી પસાર થતી અને B2Cને સમાંતર રેખા દોરો, જે લંબાવેલ BCને C’માં છેદે.
( 6 ) ∠BC’A’ = ∠BCA રચીને C’માંથી પસાર થતી અને CAને સમાંતર રેખા દોરો, જે લંબાવેલ BAને A’માં છેદે.
આથી Δ ABC’ એ માગેલ માપ મુજબનો Δ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને Δ A’BC’ની બાજુઓ Δ ABCની અનુરૂપ બાજુઓ કરતાં 1½ ગણી છે.

5. BC = 6 સેમી, AB = 5 સેમી અને ∠ABC = 60° હોય તેવો ત્રિકોણ ABC દોરો. પછી Δ ABCની અનુરૂપ બાજુઓને 3/4 પ્રમાણમાં હોય તેવી બાજુવાળા ત્રિકોણની રચના કરો.
કૃત્ય : BC = 6 સેમી, AB = 5 સેમી અને ∠ABC = 60° હોય તેવો Δ ABC દોરવો. ત્યારબાદ Δ ABCને સમરૂપ હોય તેવો એક ત્રિકોણ રચવો જેની બાજુઓનો Δ ABCની અનુરૂપ બાજુઓ સાથેનો ગુણોત્તર 3/4 હોય.

રચનાના મુદ્દા :
( 1 ) BC = 6 સેમી, AB = 5 સેમી અને ∠ABC = 60° હોય તેવો ΔABC રચો.
( 2 ) BCના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
( 3 ) BB1 = B1B2 = B2B3 = B3B4 થાય તેવાં ચાર બિંદુઓ B1, B2, B3 અને B4 ને BX પર અંક્તિ કરો.
( 4 ) B4C જોડો.
( 5 ) ∠BB3C’ = ∠BB4C રચીને B3માંથી પસાર થતી અને B4Cને સમાંતર રેખા દોરો, જે BCને C’માં છેદે.
( 6 ) ∠BC’A’ = ∠BCA રચીને C’ માંથી પસાર થતી અને CAને સમાંતર રેખા દોરો, જે BAને A’ માં છેદે.
આથી Δ A’BC’ એ માગેલ માપ મુજબનો Δ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને Δ ABCની બાજુઓ Δ ABCની અનુરૂપ બાજુઓને 3/4 પ્રમાણમાં છે.

6. BC = 7 સેમી, ∠B = 45°, ∠A = 105° હોય તેવો ત્રિકોણ ABC દોરો. પછી એવા ત્રિકોણની રચના કરો કે જેની બાજુઓ Δ ABCની અનુરૂપ બાજુઓથી 4/3 ગણી હોય.
કૃત્ય : BC = 7 સેમી, ∠B = 45° અને ∠A = 105° હોય તેવો Δ ABC રચવો. ત્યારબાદ Δ ABCને સમરૂપ હોય તેવો બીજો ત્રિકોણ રચવો, જેની બાજુઓ Δ ABCની અનુરૂપ બાજુઓથી 4/3 ગણી હોય.

રચનાના મુદ્દા :
( 1 ) BC = 7 સેમી, ∠B = 45° અને ∠C = 30° (∠C = 180° – ∠A – ∠B) હોય તેવો Δ ABC રચો.
( 2 ) BCના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્ધતલમાં કિરણ BX દોરો જેથી ∠CBX લઘુકોણ થાય.
( 3 ) BB1 = B1B2 = B2B3 = B3B4 થાય તેવાં ચાર બિંદુઓ B1, B2, B3 અને B4 ને BX ૫૨ અંક્તિ કરો.
( 4 ) B3C જોડો.
( 5 ) ∠BB4C’ = ∠BB3C રચીને B4માંથી પસાર થતી અને B3Cને સમાંતર રેખા ઘેરો, જે લંબાવેલ BCને C’માં છેદે.
( 6 ) ∠BC’A’ = ∠BCA રચીને C માંથી પસાર થતી અને CAને સમાંતર રેખા ઘેરો, જે લંબાવેલ BAને A’માં છેદે.
આથી Δ A’BC’ એ માગેલ માપ મુજબનો Δ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને Δ A’BC’ની બાજુઓ Δ ABCની અનુરૂપ બાજુઓથી 4/3 ગણી છે.

7. 4 સેમી અને 3 સેમી લંબાઈની (કર્ણ સિવાયની) બાજુવાળા કાટકોણ ત્રિકોણની રચના કરો. પછી આ ત્રિકોણની બાજુઓને અનુરૂપ તે બાજુઓથી 5/3 ગણી બાજુવાળા ત્રિકોણની રચના કરો.
કૃત્ય : AB = 3 સેમી, ∠B = 90° અને BC = 4 સેમી હોય તેવો Δ ABC રચવો. ત્યારબાદ Δ ABCને સમરૂપ હોય તેવો બીજો ત્રિકોણ રચવો, જેની બાજુઓ Δ ABCની અનુરૂપ બાજુઓથી 5/3 ગણી હોય.
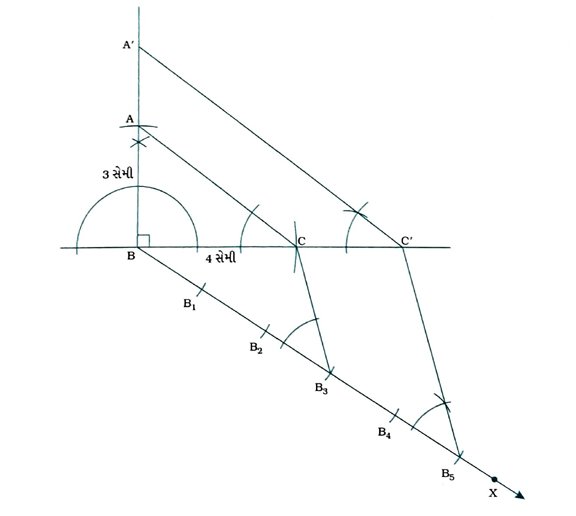
રચનાના મુદ્દા :
( 1 ) AB = 3 સેમી, ∠B = 90° અને BC = 4 સેમી હોય તેવો Δ ABC રચો.
( 2 ) BCના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્થતલમાં કિરણ BX દોરો, જેથી ∠CBX લધુકીશ થાય.
( 3 ) BB1 = B1B2 = B2B3 = B3B4 = B4B5 થાય તેવા પાંચ બિંદુઓ B1, B2, B3, B4 અને B5ને BX પર અંકિત કરો,
( 4 ) B3C જોડો, –
( 5 ) ∠BB5C’ = ∠BB3C રચીને B5 માંથી પસાર થતી અને B3Cને સમાંતર રેખા દોરો, જે લંબાવેલ BCને Cમાં છે.
( 6 ) ∠BC’A’ = ∠BCA રચીને C’ માંથી પસાર થતી અને CAને સમાંતર રેખા દોરો, જે લંબાવેલ BAને A’માં છેદે.
આથી Δ A’BC’ માગેલ માપ મુજબનો Δ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને Δ A’BC’ની બાજુઓ Δ ABCની અનુરૂપ બાજુઓથી 5/3 ગણી છે.

મહત્વનાં અન્ય ઉદાહરણો
1. BC = 4 સેમી, AC = 5 સેમી અને ∠C = 120° હોય તેવો Δ ABC દોરો. પછી એવા ત્રિકોણની રચના કરો કે જેની બાજુઓ Δ ABCની અનુરૂપ બાજુઓથી 4/5 ગણી હોય.
કૃત્ય : BC = 4 સેમી, AC = 5 સેમી અને ∠C = 120° હોય તેવો Δ ABC રચવો. ત્યારબાદ Δ ABCને સમરૂપ હોય તેવો બીજો ત્રિકોણ રચવો જેની બાજુઓ Δ ABCની અનુરૂપ બાજુઓથી 4/5 ગણી હોય.
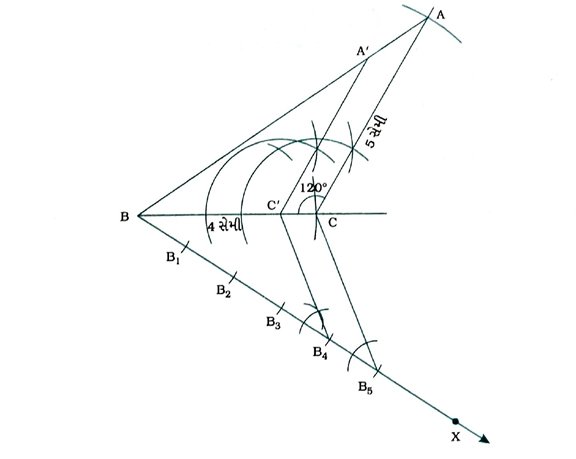
રચનાના મુદ્દા :
( 1 ) BC = 4 સેમી, AC = 5 સેમી અને ∠C = 120° હોય તેવો Δ ABC રચો.
( 2 ) BCના જે અર્ધતલમાં બિંદુ A છે તેનાથી વિરુદ્ધ અર્થતલમાં કિરણ BX દોરો, જેથી ∠CBX લઘુકોણ થાય.
( 3 ) BB1 = B1B2 = B2B3 = B3B4 = B4B5 થાય તેવા પાંચ બિંદુઓ B1, B2, B3, B4 અને B5ને BX પર અંકિત કરો,
( 4 ) B5C જોડો.
( 5 ) ∠BB4C’ = ∠BB5C રચીને B4માંથી પસાર થતી અને B5Cને સમાંતર રેખા દોરો, જે BCને C’માં છે.
( 6 ) ∠BC’A’ = ∠BCA રચીને C’માંથી પસાર થતી અને CAને સમાંતર રેખા દોરો, જે ABને A’માં છેદે.
આથી Δ A’BC’ એ માગેલ માપ મુજબનો Δ ABCને સમરૂપ હોય તેવો ત્રિકોણ છે અને Δ A’BC’ની બાજુઓ Δ ABCની અનુરૂપ બાજુઓથી 4/5 ગણી છે.
પાઠ્યપુસ્તકનાં ઉદાહરણો
* રચના 11.3: વર્તુળના બહારના બિંદુમાંથી વર્તુળના સ્પર્શકની રચના
આપણને O કેન્દ્રવાળું વર્તુળ અને તેની બહાર બિંદુ P આપ્યું છે. આપણે બિંદુ Pમાંથી વર્તુળના બે સ્પર્શકની રચના કરવી છે.
રચનાના મુદ્દા :
( 1 ) PO જોડો અને તેને દુભાગો. ધારો કે, POનું મધ્યબિંદુ M છે.
( 2 ) M કેન્દ્ર અને MOને ત્રિજ્યા લઈ એક વર્તુળ દોરો. ધારો કે, તે આપેલા વર્તુળને Q અને રમાં છેદે છે.
( 3 ) PQ અને PR જોડો
PQ અને PR એ માગેલા બે સ્પર્શક છે. (જુઓ આકૃતિ).
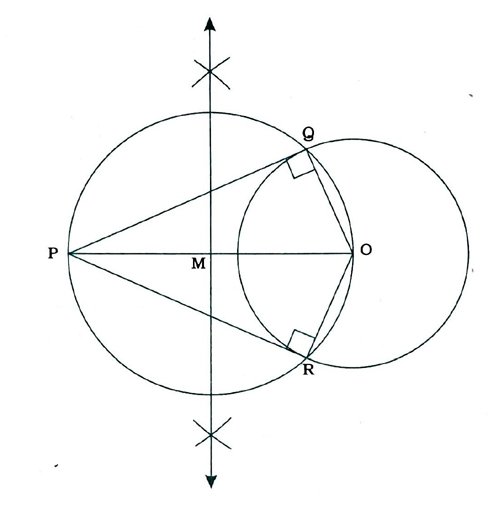
યથાર્થતા :
OQ જોડો. ∠PQO એ અર્ધવર્તુળમાંનો ખૂણો છે અને માટે ∠PQO = 90°.
આથી PQ ⊥ OQ.
આપેલ વર્તુળની ત્રિજ્યા OQ હોવાથી, PQ એ વર્તુળનો સ્પર્શક બનશે.
આ જ પ્રમાણે PR એ પણ વર્તુળનો સ્પર્શક છે.
નોંધ : જો વર્તુળનું કેન્દ્ર આપ્યું ન હોય, તો પહેલાં સમાંતર ન હોય તેવી બે જીવાઓ લઈ પછી તેમનાં લંબદ્વિભાજકોનું છેદબિંદુ શોધીએ. આ છેદબિંદુ કેન્દ્ર થશે. પછી તમે ઉ૫૨ પ્રમાણે આગળ વધી શકો.
સ્વાધ્યાય – 11.2
- નીચેની પ્રત્યેક રચના કરી, તેની રચનાના મુદ્દા તથા તેની યથાર્થતા પણ આપોઃ
1. 6 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. તેના કેન્દ્રથી 10 સેમી દૂર આવેલા બિંદુમાંથી વર્તુળના સ્પર્શકની જોડીની રચના કરો અને તેમની લંબાઈ માપો.
કૃત્ય : O કેન્દ્ર અને 6 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો અને તેની બહારના ભાગમાં બિંદુ P એવું લો જેથી OP = 10 સેમી થાય. ત્યારબાદ બિંદુ Pમાંથી વર્તુળને સ્પર્શકોની જોડ રચો તથા તે સ્પર્શકોની લંબાઈ માપો.
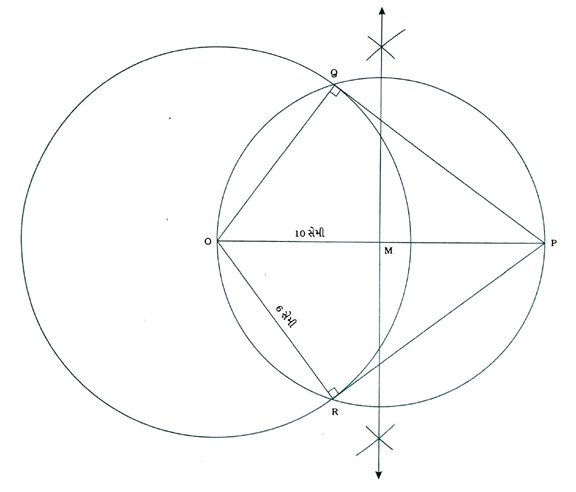
રચનાના મુદ્દા :
( 1 ) OP જોડો તથા તેનો લંબદ્વિભાજક દોરી તેનું મધ્યબિંદુ M મેળવો.
( 2 ) M કેન્દ્ર અને MO ત્રિજ્યા લઈને એક વર્તુળ દોરો, જે O કેન્દ્રવાળા વર્તુળને R અને Qમાં છેદે.
( 3 ) PQ અને PR જોડો.
PQ અને PR એ માગ્યા મુજબ બિંદુ Pમાંથી O કેન્દ્રવાળા વર્તુળને દોરેલ બે સ્પર્શકો છે. દરેક સ્પર્શકની લંબાઈ 8 સેમી છે.
એટલે કે, PQ = PR = 8 સેમી.
યથાર્થતા :
ત્રિજ્યાઓ OQ અને OR દોરો.
∠OQP અને ∠ORP એ અર્ધવર્તુળમાંના ખૂણા છે.
∴ ∠OQP = ∠ORP = 90°
આથી OQ ⊥ PQ અને OR ⊥ PR
OQ અને OR એ O કેન્દ્રિત વર્તુળની ત્રિજ્યાઓ હોવાથી, PQ અને PR એ O કેન્દ્રિત વર્તુળના સ્પર્શકો છે.
2. 4 સેમી ત્રિજ્યાવાળા વર્તુળને સમકેન્દ્રી બીજા 6 સેમી ત્રિજ્યાવાળા વર્તુળ પરના બિંદુમાંથી પ્રથમ વર્તુળના સ્પર્શકની રચના કરો અને તેની લંબાઈ માપો. વાસ્તવિક ગણતરીથી માપની ચકાસણી પણ કરો.
કૃત્ય : O કેન્દ્ર અને 4 સેમી ત્રિજ્યા તથા 6 સેમી ત્રિજ્યાવાળા બે સમકેન્દ્રી વર્તુળો દોરો. ત્યારબાદ મોટા વર્તુળ પર આવેલ બિંદુ Pમાંથી નાના વર્તુળને સ્પર્શકો દોરો તથા તે સ્પર્શકોની લંબાઈ માપો. વાસ્તવિક ગણતરીથી માપની ચકાસણી કરો.
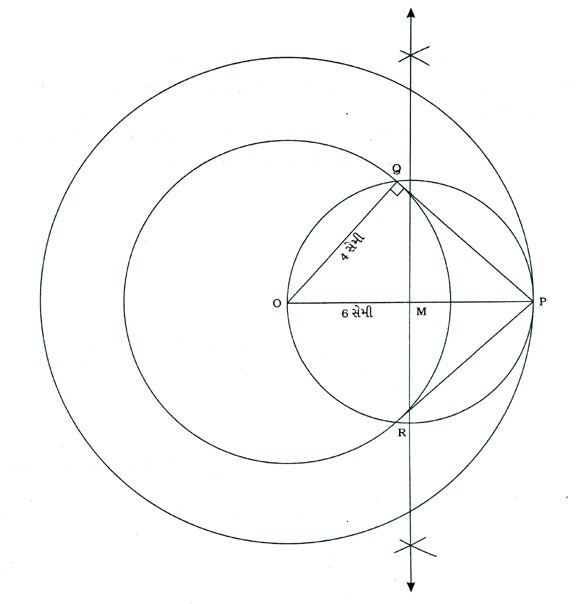
રચનાના મુદ્દા :
( 1 ) સમકેન્દ્રી વર્તુળોના કેન્દ્ર O તથા મોટા વર્તુળ પરના બિંદુ Pને જોડો.
( 2 ) OPનો લંબદ્વિભાજક દોરીને તેનું મધ્યબિંદુ M મેળવો.
( 3 ) M કેન્દ્ર તથા MO ત્રિજ્યા લઈને વર્તુળ દોરો, જે નાના વર્તુળને Q અને Rમાં છેદે.
( 4 ) PQ અને PR દોરો.
PQ અને PR એ મોટા વર્તુળ પરના બિંદુ માાંથી નાના વર્તુળના માગ્યા મુજબના સ્પર્શકો છે.
દરેક સ્પર્શકની લંબાઈ 4.5 સેમી છે.
Δ PQOમાં, ∠Q = 90°
આથી પાયથાગોરસ પ્રમેય મુજબ,
OP2 = OQ2 + PQ2

3. 3 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. તેના કેન્દ્રથી લંબાવેલા વ્યાસ પર દરેકનું અંતર 7 સેમી થાય તે રીતે બિંદુઓP અને Q લો. બિંદુઓ P અને Qમાંથી વર્તુળને સ્પર્શકો દોરો.
કૃત્ય : O કેન્દ્ર અને 3 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. તેના એક વ્યાસ XYને લંબાવી તેના પર બિંદુ P અને Q લો, જે દરેકનું કેન્દ્ર Oથી અંતર 7 સેમી હોય. ત્યારબાદ P અને Qમાંથી O કેન્દ્રવાળા વર્તુળને સ્પર્શકો દોરો.
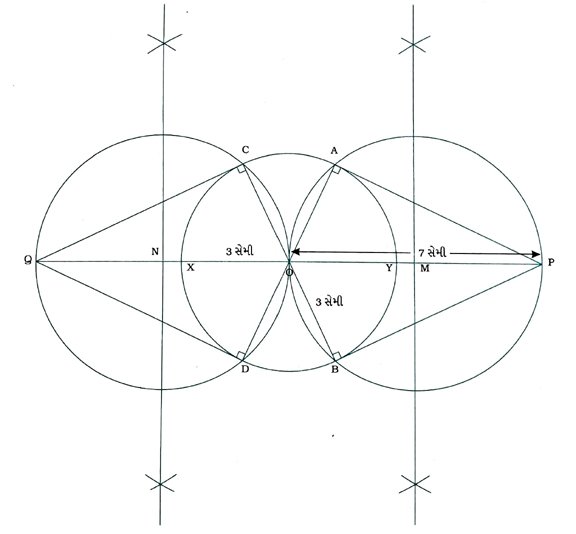
રચનાના મુદ્દા :
( 1 ) OPનો લંબદ્વિભાજક રચીને તેનું મધ્યબિંદુ M મેળવો.
( 2 ) M કેન્દ્ર અને OM ત્રિજ્યા લઈને વર્તુળ દોરો, જે O કેન્દ્રવાળા વર્તુળને A અને Bમાં છેદે.
( 3 ) PA અને PB દોરો.
PA અને PB એ બિંદુ Pમાંથી O કેન્દ્રવાળા વર્તુળના માગ્યા મુજબના સ્પર્શકો છે.
( 4 ) OQનો લંબદ્વિભાજક રચીને તેનું મધ્યબિંદુ N મેળવો.
( 5 ) N કેન્દ્ર અને ON ત્રિજ્યા લઈને વર્તુળ દોરો, જે O કેન્દ્રવાળા વર્તુળને C અને Dમાં છેદે.
( 6 ) QC અને QD દોરો.
QC અને QD એ બિંદુ Qમાંથી O કેન્દ્રવાળા વર્તુળના માગ્યા મુજબના સ્પર્શકો છે.
યથાર્થતા :
ત્રિજ્યાઓ OA, OB, OC અને OD દોરો.
અહીં, ∠PAO અને ∠PBO એ M કેન્દ્રવાળા વર્તુળના અર્ધવર્તુળમાં આવેલ ખૂણા છે. તે જ રીતે, ∠QCO અને ∠QDO એ N કેન્દ્રવાળા વર્તુળના અર્ધવર્તુળમાં આવેલ ખૂણા છે.
∴ PA ⊥ OA, PB ⊥ OB, QC ⊥ OC અને QD ⊥ OD.
આથી PA અને PB એ બિંદુ Pમાંથી દોરેલ સ્પર્શકો છે તથા QC અને QD એ બિંદુ Qમાંથી દોરેલ સ્પર્શકો છે.
4. 5 સેમી ત્રિજ્યાવાળા વર્તુળના જેમની વચ્ચેના ખૂણાનું માપ 60° થાય તેવા સ્પર્શકો રચો.
કૃત્ય : O કેન્દ્ર અને 5 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. ત્યારબાદ તે વર્તુળના એવા બે સ્પર્શકો દોરો, જેમની વચ્ચેના ખૂણાનું માપ 60° થાય.
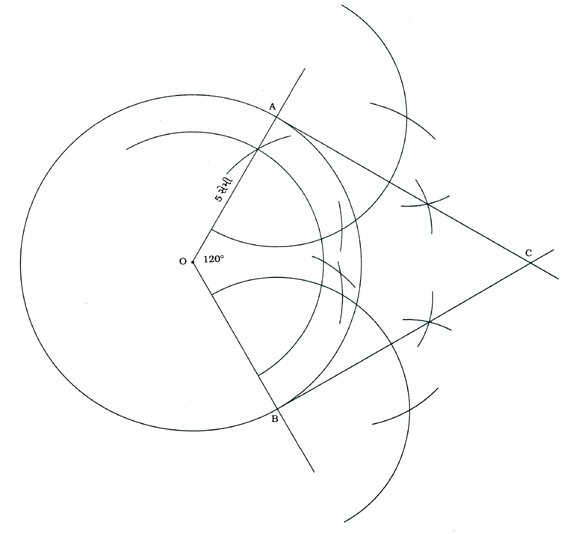
રચનાના મુદ્દા :
( 1 ) O કેન્દ્ર અને 5 સેમી ત્રિજ્યાવાળું એક વર્તુળ દોરો.
( 2 ) તે વર્તુળની ત્રિજ્યાઓ OA અને OB એવી દોરો જેથી ∠AOB = 120° (180° – 60°) થાય.
( 3 ) A અને B બિંદુએ અનુક્રમે ત્રિજ્યા OA અને OBને લંબ દોરો, જે પરસ્પર C બિંદુમાં છેદે.
આથી CA અને CB એ માગ્યા મુજબના સ્પર્શકો છે, જેમની વચ્ચેના ખૂણાનું માપ 60° છે.
યથાર્થતા :
રચના મુજબ, OA ત્રિજ્યા છે તથા AC ⊥ OA.
∴ CA એ વર્તુળનો સ્પર્શક છે અને ∠OAC = 90°.
રચના મુજબ, OB ત્રિજ્યા છે તથા BC ⊥ OB.
∴ CB એ વર્તુળનો સ્પર્શક છે અને ∠OBC = 90°.
ચતુષ્કોણ OACBમાં,
∠AOB + ∠OAC + ∠OBC + ∠ACB = 360°
∴ 120° + 90° + 90° + ∠ACB = 360°
∴ ∠ACB = 60°
આમ, સ્પર્શકો CA અને CBની વચ્ચેના ખૂણાનું માપ 60° છે.
5. 8 સેમી લંબાઈનો રેખાખંડ AB દોરો. Aને કેન્દ્ર લઈ 4 સેમી ત્રિજ્યાવાળું એક વર્તુળ દોરો. Bને કેન્દ્ર લઈ બીજું 3 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. પ્રત્યેક વર્તુળને બીજા વર્તુળના કેન્દ્રમાંથી સ્પર્શકો દોરો.
કૃત્ય : 8 સેમી લંબાઈનો રેખાખંડ AB દોરો. A કેન્દ્ર અને 4 સેમી ત્રિજ્યાવાળું વર્તુળ તથા B કેન્દ્ર અને 3 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. પ્રત્યેક વર્તુળને બીજા વર્તુળના કેન્દ્રમાંથી સ્પર્શકો દોરો.

રચનાના મુદ્દા :
( 1 ) 8 સેમી લંબાઈનો રેખાખંડ AB દોરો. A કેન્દ્ર અને 4 સેમી ત્રિજ્યાવાળું વર્તુળ તથા B કેન્દ્ર અને 3 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો.
( 2 ) ABનો લંબદ્વિભાજક રચીને તેનું મધ્યબિંદુ M મેળવો.
( 3 ) M કેન્દ્ર અને MA (MB) ત્રિજ્યાવાળું વર્તુળ દોરો, જે B કેન્દ્રવાળા વર્તુળને R તથા Sમાં છેદે અને A કેન્દ્રવાળા વર્તુળને P તથા ડુમાં છેદે.
( 4 ) AR તથા AS જોડો. BP અને BQ પણ જોડો.
આથી AR તથા AS એ બિંદુ Aમાંથી B કેન્દ્રવાળા વર્તુળના સ્પર્શકો છે તથા BP અને BQ એ બિંદુ Bમાંથી A કેન્દ્રવાળા વર્તુળના સ્પર્શકો છે.
યથાર્થતા :
B કેન્દ્રવાળા વર્તુળની ત્રિજ્યાઓ BR અને BS દોરો.
∠ARB અને ∠ASB એ M કેન્દ્રવાળા વર્તુળના અર્ધવર્તુળમાં આવેલ ખૂણાઓ છે.
∴ ∠ARB = ∠ASB = 90°
∴ AR ⊥ BR અને AS ⊥ BS
આથી AR અને AS એ બિંદુ Aમાંથી B કેન્દ્રવાળા વર્તુળના સ્પર્શકો છે.
A કેન્દ્રવાળા વર્તુળની ત્રિજ્યાઓ AP અને AQ દોરો.
∠APB અને ∠AQB એ M કેન્દ્રવાળા વર્તુળના અર્ધવર્તુળમાં આવેલ ખૂણાઓ છે.
∴ ∠APB = ∠AQB = 90°
∴ BP ⊥ AP અને BQ ⊥ AQ
આથી BP અને BQ એ બિંદુ Bમાંથી A કેન્દ્રવાળા વર્તુળના સ્પર્શકો છે.
6. AB = 6 સેમી, BC = 8 સેમી અને ∠B = 90° થાય તેવો કાટકોણ ત્રિકોણ ABC લો. Bમાંથી AC પરનો લંબ BD છે. B, C, Dમાંથી પસાર થતું વર્તુળ દોરેલું છે. Aમાંથી આ વર્તુળને સ્પર્શકો દોરો.
કૃત્ય : AB = 6 સેમી, BC = 8 સેમી અને ∠B = 90° હોય તેવો Δ ABC દોરો. Bમાંથી AC પરનો વેધ BD દોરો. B, C અને Dમાંથી પસાર થતું વર્તુળ દોરો. ત્યારબાદ Aમાંથી આ વર્તુળને સ્પર્શકો દોરો.
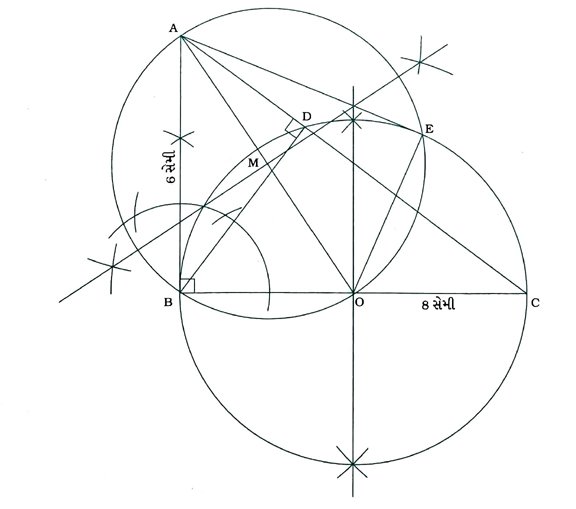
રચનાના મુદ્દા :
( 1 ) AB = 6 સેમી, BC = 8 સેમી અને ∠B = 90° હોય તેવો Δ ABC દોરો. Bમાંથી AC પરનો વેધ BD દોરો.
( 2 ) BCનો લંબદ્વિભાજક રચી તેનું મધ્યબિંદુ O મેળવો. BC વ્યાસ હોય તેવું વર્તુળ દોરો. ∠BDC કાટખૂણો હોવાથી આ વર્તુળ Dમાંથી પસાર થશે જ.
( 3 ) AO જોડો અને તેનો લંબદ્વિભાજક રચીને તેનું મધ્યબિંદુ M મેળવો.
( 4 ) M કેન્દ્ર અને MA ત્રિજ્યાવાળું વર્તુળ દોરો, જે BC વ્યાસવાળા વર્તુળને B અને Eમાં છેદે.
( 5 ) AE જોડો.
આથી AB અને AE એ માગ્યા મુજબ B, C અને Dમાંથી પસાર થતા વર્તુળને બિંદુ Aમાંથી દોરેલા સ્પર્શકો છે.
યથાર્થતા :
OB એ B, C અને Dમાંથી પસાર થતા વર્તુળની ત્રિજ્યા છે અને ∠ABO (એટલે કે Δ ABCનો ∠ABC) = 90°.
આથી AB ⊥ OB.
આમ, AB એ સ્પર્શક છે.
હવે, ∠AEO એ અર્ધવર્તુળનો અંતર્ગત ખૂણો છે.
∴ ∠AEO = 90° તથા OE એ B, C અને Dમાંથી પસાર થતા વર્તુળની ત્રિજ્યા છે.
∴ AE ⊥ OE
આમ, AE એ સ્પર્શક છે.
વૈકલ્પિક રીત :
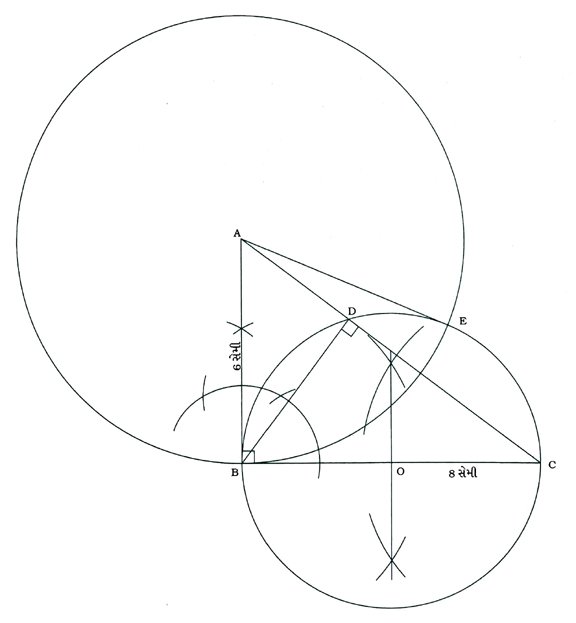
રચનાના મુદ્દા :
( 1 ) AB = 6 સેમી, BC = 8 સેમી અને ∠B = 90° હોય તેવો Δ ABC દોરો. Bમાંથી AC પરનો વેધ BD દોરો.
( 2 ) BCનો લંબદ્વિભાજક રચી તેનું મધ્યબિંદુ O મેળવો.
BC વ્યાસ હોય તેવું વર્તુળ દોરો. ∠BDC કાટખૂણો હોવાથી આ વર્તુળ Dમાંથી પસાર થશે જ.
( 3 ) A કેન્દ્ર અને AB ત્રિજ્યાવાળું વર્તુળ દોરો, જે BC વ્યાસવાળા વર્તુળને Eમાં છેદે.
( 4 ) AE જોડો.
આથી AB અને AE એ માગ્યા મુજબ B, C અને Dમાંથી પસાર થતા વર્તુળને બિંદુ Aમાંથી દોરેલા સ્પર્શકો છે.
યથાર્થતા :
OB એ B, C અને Dમાંથી પસાર થતા વર્તુળની ત્રિજ્યા છે અને ∠ABO (એટલે કે AABCનો ∠ABC) = 90°.
આથી AB ⊥ OB.
આમ, AB એ સ્પર્શક છે.
હવે, AB = AE = A કેન્દ્રવાળા વર્તુળની ત્રિજ્યા અને બિંદુ E એ B, C અને Dમાંથી પસાર થતા વર્તુળ પરનું બિંદુ છે. આપણે જાણીએ છીએ વર્તુળની બહારના ભાગમાં આવેલ બિંદુમાંથી વર્તુળને દોરેલા સ્પર્શકો સમાન હોય છે.
આમ, AE એ સ્પર્શક છે.
7. બંગડીની મદદ લઈ એક વર્તુળ દોરો. વર્તુળની બહાર એક બિંદુ લો. આ બિંદુમાંથી વર્તુળના સ્પર્શકોની જોડ દોરો.
કૃત્ય : બંગડીની મદદ લઈ એક વર્તુળ દોરો. વર્તુળની બહાર એક બિંદુ P લો. ત્યારબાદ બિંદુ માાંથી વર્તુળને સ્પર્શકોની જોડ દોરો.
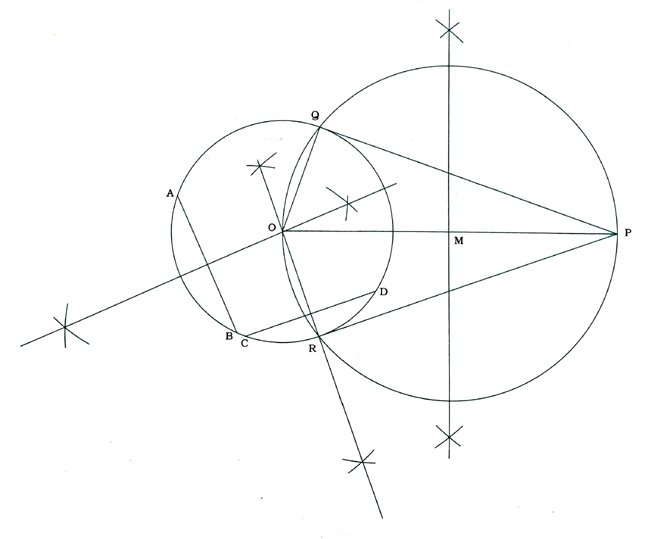
રચનાના મુદ્દા ;
( 1 ) બંગડીની મદદથી એક વર્તુળ ઘેરો અને તેની બહાર એક બિંદુ P લો, વર્તુળમાં સમાંતર ન હોય તેવી બે જીવાઓ AB અને CD દોરો,
( 2 ) AB અને CDના લંઢિભાજકો ઘેરો, જે પરસ્પર O બિંદુમાં છંટે. આ બિંદુ O એ વર્તુળનું કેન્દ્ર છે.
( 3 ) OP જોડો અને તેનો લંઢિભાજક રચી તેનું મધ્યબિંદુ M મેળવો.
( 4 ) M કેન્દ્ર અને MP ત્રિજ્યાવાળું વર્તુળ દ્યો, જે આગળ દોરેલ વર્તુળને R અને Qમાં છેદે.
( 5 ) PR. અને PQ દોરો.
આમ, PR અને PQ એ બંગડીની મદદથી દોરેલ વર્તુળને બિંદુ Pમાંથી ઘેરેલા સ્પર્શો છે.
યથાર્થતા :
બિંદુ O એ જીવા AB તેમજ જીવા CDના લંબદ્ધભાજક પરનું બિંદુ હોવાથી O એ A, B, C અને Dમાંથી પસાર થતા વર્તુળનું કેન્દ્ર છે.
OR અને OQ દોરો.
∠PRO એ અર્ધવર્તુળમાં અંતર્ગત ખુલ્લો છે.
∴ ∠PRO = 90°
∴ PR ⊥ OR
આમ, PR એ સ્પર્શક છે,
∠PQO એ અર્ધવર્તુળમાં અંતર્ગત ખુણો છે.
∴ ∠PQO = 90°
∴ PQ ⊥ OQ
આમ, PQ એ સ્પર્શક છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
1, 4 સેમી ત્રિજ્યાવાળા વર્તુળના એવા સ્પર્શકો રચો જેમની વચ્ચેના ખૂણાનું માપ 45° હોય.
કૃત્ય : P કેન્દ્ર અને 4 સેમી ત્રિજ્યાવાળું વર્તુળ ઘેરો. ત્યારબાદ તે વર્તુળના એવા બે સ્પર્શકો દોરો, જેમની વચ્ચેના ખૂણાનું માપ 45° થાય.
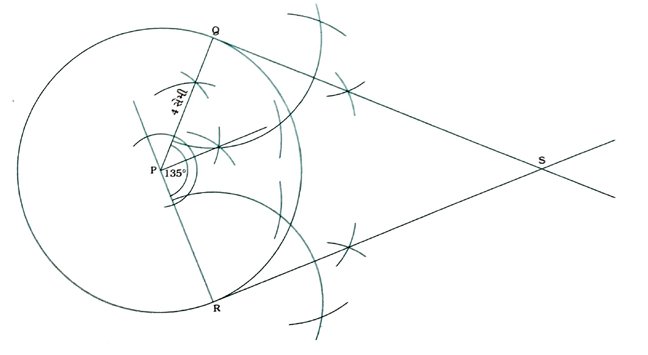
રચનાના મુદ્દા :
( 1 ) P કેન્દ્ર અને 4 સેમી ત્રિજ્યાવાળું એક વર્તુળ દોરો.
( 2 ) તે વર્તુળની ત્રિજ્યાઓ PQ અને PR એવી દોરો, જેથી ∠QPR = 135° (180° – 45°) થાય.
( 3 ) Q અને R બિંદુએ અનુક્રમે ત્રિજ્યા PQ અને PRને લંબ દોરો, જે પરસ્પર S બિંદુમાં છેદે.
આથી SQ અને SR એ માગ્યા મુજબના સ્પર્શકો છે, જેમની વચ્ચેના ખૂણાનું માપ 45° છે.
યથાર્થતા :
રચના મુજબ, PQ ત્રિજ્યા છે તથા SQ ⊥ PQ.
∴ SQ એ વર્તુળનો સ્પર્શક છે અને ∠PQS = 90°.
રચના મુજબ, PR ત્રિજ્યા છે તથા SR ⊥ PR.
∴ SR એ વર્તુળનો સ્પર્શક છે અને ∠PRS = 90°.
ચતુષ્કોણ QPRSમાં,
∠QPR + ∠PQS + ∠PRS + ∠QSR = 360°
∴ 135° + 90° + 90° + ∠QSR = 360°
∴ ∠QSR = 45°
આમ, સ્પર્શકો SQ અને SRની વચ્ચેના ખૂણાનું માપ 45° છે.
કૌશલ્ય ચકાસણી
- નીચેની પ્રત્યેક રચના કરી, તેની રચનાના મુદ્દા તથા તેની યથાર્થતા આપો :
1. 5 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. તેના કેન્દ્રથી 9સેમી દૂર આવેલા બિંદુમાંથી વર્તુળના સ્પર્શકોની જોડ રચો.
2. 4 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. તેના કેન્દ્રથી 10 સેમી દૂર આવેલા બિંદુમાંથી વર્તુળના સ્પર્શકોની જોડ રચો.
3. 4 સેમી ત્રિજ્યાવાળું એક વર્તુળ દોરી, તેનો એક વ્યાસ AB દોરો. ABને બંને તરફ લંબાવી તેના બંને ભાગ પર એક-એક બિંદુ લો. આ દરેક બિંદુમાંથી વર્તુળના સ્પર્શકોની જોડ રચો.
4. 10સેમી લંબાઈનો રેખાખંડ AB દોરો. A કેન્દ્ર અને 4 સેમી ત્રિજ્યાવાળું વર્તુળ તથા B કેન્દ્ર અને 3 સેમી ત્રિજ્યાવાળું વર્તુળ દોરો. દરેક વર્તુળને બીજા વર્તુળના કેન્દ્રમાંથી સ્પર્શકોની જોડ રચો.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
( 1 ) જો કોઈ વર્તુળને દોરવાના બે સ્પર્શકો વચ્ચેના ખૂણાનું માપ 35° હોય, તો તે સ્પર્શકો એવી ત્રિજ્યાઓના વર્તુળ પરના અંત્યબિંદુએ લંબ દોરવાથી મળે, જે ત્રિજ્યાઓ વચ્ચેના ખૂણાનું માપ …….. હોય.
( 2 ) આપેલ રેખાખંડનું √3 : 1/√3 ગુણોત્તરમાં વિભાજન કરવું અને તેનું ……. ગુણોત્તરમાં વિભાજન કરવું તે સમાન બાબત છે.
( 3 ) O કેન્દ્ર અને 4 સેમી ત્રિજ્યાવાળા વર્તુળના સમતલમાં બિંદુ P એવું છે. જેથી OP = 3 સેમી થાય. Pમાંથી આપેલ વર્તુળને સ્પર્શક દોરવા …….. છે.
( 4 ) કોઈ વર્તુળના એક વ્યાસના અંત્યબિંદુમાંથી દોરેલા વર્તુળના સ્પર્શકો પરસ્પર …….. હોય.
( 5 ) એક વર્તુળની બે ત્રિજ્યાઓ વચ્ચેના ખૂણાનું માપ 70° છે. આ ત્રિજ્યાઓના અંત્યબિંદુએ દોરેલા સ્પર્શકો વચ્ચેના ખૂણાનું માપ ……….. થાય.
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
( 1 ) રેખાખંડ ABનું 3: 5 ગુણોત્તરમાં વિભાજન કરવા તેની એક બાજુના અર્ધતલમાં કિરણ AX એવું દોરેલ છે, જેથી ∠BAX લઘુકોણ થાય. AX પર સમાન અંતરે હોય તેવાં ઓછામાં ઓછાં …… બિંદુઓ અંકિત કરવાં પડે.
A. 3
B. 5
C. 8
D. 15
( 2 ) Δ ABCને સમરૂપ અને સ્કેલમાપન 3/7 હોય તેવો ત્રિકોણ રચવા માટે BCનું ……. ગુણોત્ત૨માં વિભાજન કરવું પડે.
A. 3 : 4
B. 3 : 7
C. 3 : 10
D. 4 : 7
( 3 ) રેખાખંડ AB પર આવેલ બિંદુ P એવું છે કે જેથી AP/AB = 2/5 થાય. આથી બિંદુ Pએ ABનું …….. ગુણોત્ત૨માં અંતર્વિભાજન કરે છે.
A. 2 : 5
B. 2 : 3
C. 3 : 5
D. 5 : 2
( 4 ) રેખાખંડ AB પર આવેલ બિંદુ P એવું છે કે જેથી 7PB = 3AB થાય. આથી AP : PB = ………. થાય.
A. 4 : 7
B. 7 : 4
C. 7 : 3
D. 4 : 3
( 5 ) આપેલ રેખાખંડનું 4: 7 ગુણોત્તરમાં અંતર્વિભાજન કરવા માટે, રેખાખંડ સાથે લઘુકોણ રચતા કિરણ પર સરખા અંતરે …… બિંદુઓ અંકિત કરવાં પડે.
A. 4
B. 7
C. 11
D. 28
( 6 ) એક વર્તુળને એવા બે સ્પર્શકો દોરવા છે કે જેમની વચ્ચેના ખૂણાનું માપ 60° હોય. આ સ્પર્શકો એવી ત્રિજ્યાઓના વર્તુળ પરના અંત્યબિંદુમાંથી દોરેલા લંબ દ્વારા મળે, જે ત્રિજ્યાઓની વચ્ચેના ખૂણાનું માપ ……… હોય.
A. 60°
B. 120°
C. 90°
D. 75°
( 7 ) એક વર્તુળના પરસ્પર લંબ હોય તેવા સ્પર્શકો દોરવા માટે એવી બે ત્રિજ્યાના અંત્યબિંદુમાંથી લંબ દોરવા જોઈએ, જે ત્રિજ્યાઓ વચ્ચેના ખૂણાનું માપ ……… હોય.
A. 120°
B. 60°
C. 30°
D. 90°
( 8 ) જો કોઈ વર્તુળના બે સ્પર્શકો વચ્ચેના ખૂણાનું માપ 35॰ હોય, તો તે સ્પર્શકોના સ્પર્શબિંદુમાંથી દોરેલી ત્રિજ્યાઓ વચ્ચેના ખૂણાનું માપ ……… હોય.
A. 35°
B. 55°
C. 125°
D. 145°
( 9 ) O કેન્દ્ર અને 3 સેમી ત્રિજ્યાના સમતલમાં બિંદુ P એવું છે, જેથી OP = 8 સેમી થાય. Pમાંથી વર્તુળને સ્પર્શકો દોરવા આપણે OPના મધ્યબિંદુને કેન્દ્ર તથા ……… સેમી ત્રિજ્યાવાળું વર્તુળ દોરવું જોઈએ.
A. 8
B. 3
C. 5
D. 4
( 10 ) જો કોઈ વર્તુળના બે સ્પર્શકો વચ્ચેના ખૂણાનું માપ 75° હોય, તો તે સ્પર્શકોના સ્પર્શબિંદુમાંથી દોરેલી ત્રિજ્યાઓ વચ્ચેના ખૂણાનું માપ …….. હોય.
A. 15°
B. 75°
C. 105°
D. 125°
3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ લખો :
( 1 ) બિંદુ P એ O કેન્દ્ર અને 5 સેમી ત્રિજ્યાવાળા વર્તુળની બહારના ભાગમાં આવેલ બિંદુ છે. જો OP = 13 સેમી હોય, તો Pમાંથી દોરેલ વર્તુળના સ્પર્શકની લંબાઈ કેટલી હોય?
( 2 ) રેખાખંડ AB પર આવેલ બિંદુ P એવું છે કે જેથી AP/AB = 3/8 થાય. બિંદુ P એ ABનું કયા ગુણોત્તરમાં વિભાજન કરે છે?
( 3 ) એક વર્તુળના બે સ્પર્શકો વચ્ચેના ખૂણાનું માપ 140° છે. એ બે સ્પર્શકોના સ્પર્શબિંદુમાંથી દોરેલ ત્રિજ્યાઓ વચ્ચેના ખૂણાનું માપ કેટલું હોય?
( 4 ) રેખાખંડ AB પરનું બિંદુ P એવું છે કે જેથી 3AB = 10AP થાય. બિંદુ P એ ABનું કયા ગુણોત્તરમાં વિભાજન કરે છે?
( 5 ) Δ ABCને સમરૂપ હોય તથા સ્કેલમાપન 4/7 હોય તેવો ત્રિકોણ રચવા માટે BCનું કયા ગુણોત્તરમાં વિભાજન કરવું જોઈએ?
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) આપેલ રેખાખંડનું √5 : 1/√5 ગુણોત્તરમાં વિભાજન કરવું શક્ય છે.
( 2 ) આપેલ રેખાખંડનું 2 + √3 : 2 – √3 ગુણોત્તરમાં વિભાજન કરવું શક્ય છે.
[સૂચન : આપેલ ગુણોત્તરને સાદું રૂપ આપીને પૂર્ણાંકોનો ગુણોત્તર મેળવી શકાતો નથી.]
( 3 ) 5 સેમી ત્રિજ્યાવાળા વર્તુળના કેન્દ્રથી 4 સેમી અંતરે આવેલા બિંદુ Pમાંથી વર્તુળને બે સ્પર્શકો દોરી શકાય.
( 4 ) 4 સેમી ત્રિજ્યાવાળા વર્તુળના કેન્દ્રથી 8સેમી અંતરે આવેલા બિંદુ Pમાંથી વર્તુળને બે સ્પર્શકો દોરી શકાય.
( 5 ) વર્તુળને એવા બે સ્પર્શકો દોરી શકાય જેમની વચ્ચેના ખૂણાનું માપ 170° હોય.
જવાબ :
1. ( 1 ) 145° ( 2 ) 3 : 1 ( 3 ) અશક્ય ( 4 ) સમાંતર ( 5 ) 1 10°
2. ( 1 ) 8 ( 2 ) 3 : 4 ( 3 ) 2 : 3 ( 4 ) 4 : 3 ( 5 ) 11 ( 6 ) 120° ( 7 ) 90° ( 8 ) 145° ( 9 ) 4 ( 10 ) 105°
3. ( 1 ) 12 સેમી ( 2 ) 3 : 5 ( 3 ) 40° ( 4 ) 3 : 7 ( 5 ) 4 : 3
4. ( 1 ) ખરું ( 2 ) ખોટું ( 3 ) ખોટું ( 4 ) ખરું ( 5 ) ખરું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here