Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 1 Real Numbers (વાસ્તવિક સંખ્યાઓ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 1 Real Numbers (વાસ્તવિક સંખ્યાઓ)
સ્વાધ્યાય – 1.1
1. યુક્લિડની ભાગપ્રવિધિનો ઉપયોગ કરી ગુ.સા.અ. શોધો :
(1) 135 અને 225 (2) 196 અને 38220 (3) 867 અને 255
(1) 135 અને 225
અહીં, 225 > 135
∴ 225 = 135 × 1 + 90
શેષ ≠ 0 હોવાથી આપણે 135 અને 90 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
135 = 90 × 1 + 45
શેષ ≠ 0 હોવાથી આપણે 90 અને 45 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
90 = 45 × 2 + 0
હવે, શેષ = 0 હોવાથી ભાજક 45 એ માગેલ ગુ.સા.અ. છે.
આમ, ગુ.સા.અ. (135, 225) = 45
(2) 196 અને 38220
અહીં, 38220 > 196
∴ 38220 = 196 × 195 + 0
હવે, શેષ = 0 હોવાથી ભાજક 196 એ માગેલ ગુ.સા.અ. છે.
આમ, ગુ.સા.અ. (196, 38220) = 196
(3) 867 અને 255
અહીં, 867 > 255
∴ 867 = 255 × 3 + 102
શેષ ≠ 0 હોવાથી આપણે 255 અને 102 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
255 = 102 × 2 + 51
શેષ ≠ 0 હોવાથી આપણે 102 અને 51 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
102 = 51 × 2 + 0
શેષ = 0 હોવાથી ભાજક 51 એ માગેલ ગુ.સા.અ. છે.
આમ, ગુ.સા.અ. (867, 255) = 51
2. દર્શાવો કે, કોઈ પણ અયુગ્મ ધન પૂર્ણાંક સંખ્યા કોઈક પૂર્ણાંક q માટે, 6q + 1 અથવા 6q + 3 અથવા 6q + 5 પ્રકારની હોઈ શકે.
ધારો કે, a એ કોઈ અયુગ્મ ધન પૂર્ણાંક સંખ્યા છે અને b = 6. હવે, યુક્લિડના ભાગાકારના પૂર્વપ્રમેય અનુસાર a = 6q + r, જ્યાં q કોઈ પૂર્ણાંક છે અને r = 0, 1, 2, 3, 4 અથવા 5, કારણ કે, 0 ≤ r < 6.
માટે, a = 6q અથવા a = 6q + 1 અથવા
a = 6q + 2 અથવા a = – 6q + 3 અથવા
a = 6q + 4 અથવા a = – 6q + 5.
પરંતુ, 6q, 6q + 2 અને 6q +4 દરેક 2 વડે વિભાજ્ય છે અને a એ અયુગ્મ હોવાથી a = 6q અથવા a = 6q + 2 અથવા a = 6q + 4 શક્ય નથી.
આથી કોઈ પણ અયુગ્મ ધન પૂર્ણાંક સંખ્યા, કોઈક પૂર્ણાંક q માટે 6q + 1 અથવા 6q + 3 અથવા 6q + 5 પ્રકારની જ હોય.
3. એક લશ્કરનું 616 સભ્યોનું જૂથ લશ્કરના બૅન્ડના 32 સભ્યોની પાછળ કૂચ કરી રહ્યું છે. બંને જૂથ સમાન સંખ્યાના સ્તંભમાં કૂચ કરી રહ્યાં છે. તેઓ જે સ્તંભમાં કૂચ કરી રહ્યા છે તેવા કોઈ પણ સ્તંભમાં મહત્તમ કેટલા સભ્યો હશે?
આપેલ પ્રશ્નનો જવાબ આપવા આપણે 616 અને 32નો ગુ.સા.અ. શોધવો જોઈએ.
અહીં, 616 > 32
∴ 616 = 32 × 19 +8
∴ 32 = 8 × 4 + 0
આમ, ગુ.સા.અ. (616, 32) = 8
આમ, તેઓ જે સ્તંભમાં કૂચ કરી રહ્યાં છે તેવા કોઈ પણ સ્તંભમાં મહત્તમ 8 સભ્યો હશે.
4. યુક્લિડના ભાગાકારના પૂર્વપ્રમેયનો ઉપયોગ કરી દર્શાવો કે, કોઈ પણ ધન પૂર્ણાંકનો વર્ગ કોઈક પૂર્ણાંક m માટે, 3m અથવા 3m + 1 સ્વરૂપમાં હોય.
[સૂચન : ધારો કે, × કોઈ ધન પૂર્ણાંક છે, તો તે 3q, 3q + 1 x અથવા 3q + 2 સ્વરૂપમાં હોય. હવે, દરેકનો વર્ગ કરો અને દર્શાવો કે ફરીથી તેને 3m અથવા 3m + 1 સ્વરૂપમાં લખી શકાય.]
ધારો કે, a કોઈ પણ ધન પૂર્ણાંક છે અને b = 3.
હવે, યુક્લિડના ભાગાકારના પૂર્વપ્રમેય અનુસાર a = 3q અથવા a = 3q + 1 અથવા a = 3q + 2. જ્યાં, q કોઈ પૂર્ણાંક છે.
(1) જો a = 3q, તો
a2 = (3q)2 = 9q2 = 3 (3q2) = 3m,
જ્યાં, m = 3q2 કોઈ પૂર્ણાંક છે.
(2) જો a = 3q + 1, તો
a2 = (3q + 1)2
= 9q2 + 6q + 1
= 3 (3q² + 2q) + 1 = 3m + 1
જ્યાં, m = 3q2 + 2q કોઈ પૂર્ણાંક છે.
(3) જો a = 3q + 2, તો
a2 = (3q + 2)2
= 9q² + 12q + 4
= 9q2 + 12q + 3 + 1
= 3 (3q2 + 4q + 1) + 1 = 3m + 1
જ્યાં, m = 3q2 + 4q + 1 કોઈ પૂર્ણાંક છે.
આમ, કોઈ પણ સંજોગોમાં, કોઈ પણ ધન પૂર્ણાંકનો વર્ગ કોઈક પૂર્ણાંક m માટે 3m અથવા 3m + 1 સ્વરૂપમાં હોય.
5. યુક્લિડનું ભાગાકારનું પૂર્વપ્રમેય વાપરીને દર્શાવો કે, કોઈ પણ ધન પૂર્ણાંકનો ઘન 9m, 9m + 1 અથવા 9m + 8 સ્વરૂપનો હોય.
ધારો કે, a કોઈ પણ ધન પૂર્ણાંક છે અને b = 3. હવે, યુક્લિડના ભાગાકારના પૂર્વપ્રમેય અનુસાર a = 3q અથવા a = 3q + 1 અથવા a = 3q + 2. જ્યાં, q કોઈ પૂર્ણાંક છે.
(1) જો a = 3q, તો
a3 = (3q)3 = 27q3 = 9 (3q3) = 9m
જ્યાં, m = 3q3 કોઈ પૂર્ણાંક છે.
(2) જો a = 3q + 1, તો
a3 = (3q + 1)3
= 27q³ + 27q² + 9q + 1
= 9 (3q³ + 3q² + q) + 1 = 9m + 1
જ્યાં, m = 3q3 + 3q2 + q કોઈ પૂર્ણાંક છે.
(3) જો a = 3q + 2, તો
a3 = (3q + 2)3
= 27q3 + 54q2 + 36q + 8
= 9 (3q3 + 6q2 + 4q) + 8 = 9m + 8
જ્યાં, m = 3q3 + 6q2 + 4q કોઈ પૂર્ણાંક છે.
આમ, કોઈ પણ સંજોગોમાં, કોઈ પણ ધન પૂર્ણાંકનો ઘન 9m અથવા 9m + 1 અથવા 9m + 8 સ્વરૂપનો હોય.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. એક ઓરડાની લંબાઈ, પહોળાઈ અને ઊંચાઈ અનુક્રમે 7મી 50 સેમી, 6 મી અને ૩ મી 75 સેમી છે. આ ત્રણેય માપને ચોક્કસ માપી શકાય તેવા લાંબામાં લાંબા સળિયાની લંબાઈ શોધો.
અહીં, ત્રણેય માપનો ગુ.સા.અ. લેતાં માગ્યા મુજબના લાંબામાં લાંબા સળિયાની લંબાઈ મળે.
હવે, 7 મી 50 સેમી = 750 સેમી, 6 મી = 600 સેમી અને 3 મી 75 સેમી = 375 સેમી.
ભાગપ્રવિધિના ઉપયોગથી ત્રણ સંખ્યાનો ગુ.સા.અ. શોધવા માટે પ્રથમ તે ત્રણ પૈકી કોઈ પણ બે સંખ્યાનો ગુ.સા.અ. શોધવો જોઈએ. ત્યારબાદ તે ગુ.સા.અ. અને ત્રીજી સંખ્યાનો ગુ.સા.અ. લેતાં ત્રણેય સંખ્યાનો ગુ.સા.અ. મળે.
750 = 600 × 1 + 150
600 = 150 × 4 + 0
∴ ગુ.સા.અ. (750, 600) = 150
હવે, આપણે 375 અને 150નો ગુ.સા.અ. શોધીએ.
375 = 150 × 2 + 75
150 = 75 × 2 + 0
∴ ગુ.સા.અ. (375, 150) = 75
આથી ગુ.સા.અ. (750, 600, 375) = 75
આમ, ઓરડાના ત્રણેય માપને ચોક્કસ માપી શકાય તેવા લાંબામાં લાંબા સળિયાની લંબાઈ 75 સેમી છે.
2. સાબિત કરો કે, કોઈ પણ ધન પૂર્ણાંક અને તેના વર્ગનો સરવાળો યુગ્મ સંખ્યા જ હોય.
ધારો કે, તુ કોઈ પણ ધન પૂર્ણાંક છે અને b = 2,
માટે a = 2q અથવા a = 2q + 1 જ્યાં, q કોઈ પૂર્ણાંક છે,
હવે, a તથા તેના વર્ગ વºનો સરવાળો
= a2 + a = a (a + 1)
જો a = 2q, તો a2 + a = a (a + 1) = 2q (2q + 1) જેમાં 2 અવયવ હોવાથી યુગ્મ સંખ્યા છે.
જો a = 2q + 1, તો
a2 + a = a (a + 1) = (2q + 1) (2q + 1 + 1)
= 2 (24 + 1) (9 + 1)માં પણ 2
અવયવ હોવાથી યુગ્મ સંખ્યા છે,
આમ, કોઈ પણ ધન પૂર્ણાંક અને તેના વર્ગનો સરવાળો યુગ્મ સંખ્યા જ હોય.
3. સાબિત કરી કે, કોઈ પણ ધન પૂર્ણાંકનો વર્ગ 5m અથવા 5m ± 1 સ્વરૂપનો હોય.
ધારો કે, a કોઈ ધન પૂર્ણાંક છે અને b = 5, તો યુક્લિડના ભાગાકારના પૂર્વપ્રમેય અનુસાર,
a = 5q અથવા a = 5q + 1 અથવા a = 5q + 2 અથવા a = 5q + 3 અથવા a = 5q + 4 જ્યાં, q કોઈ પૂર્ણાંક છે.
(1) જો a = 5q, તો
a2 = (5q)2 = 25q2 = 5 (5q2) = 5m
જ્યાં, m = 5q2 એ પૂર્ણાંક છે.
(2) જો a = 5q ) + 1, તો
a2 = (5q + 1)2
= 25q² + 10q + 1
= 5 (5q2 + 2q) + 1 = 5m + 1
જ્યાં, m = 5q2 + 2q એ પૂર્ણાંક છે.
(3) જો a = 5q + 2, તો
a2 = (5q + 2)2
= 25q2 + 20q + 4
= 25q² + 20q + 5 – 1
= 5 (5q2 + 4q + 1) – 1 = 5m – 1
જ્યાં, m = 5q2 + 4q + 1 એ પૂર્ણાંક છે.
(4) જો a = 5q + 3, તો
a2 = (5q + 3)2
= 25q2 + 30q + 9
= 25q2 + 30q + 10 – 1
= 5 (5q2 + 6q + 2) – 1 = 5m – 1
જ્યાં, m = 5q2 + 6q + 2 એ પૂર્ણાંક છે.
(5) જો a = 5q + 4, તો
a2 = (5q + 4)2
= 25q2 + 40q + 16
= 25q2 + 40q + 15 + 1
= 5 (5q2 + 8q + 3) + 1 = 5m + 1
જ્યાં, m = 5q2 + 8q + 3 એ પૂર્ણાંક છે.
આમ, કોઈ પણ ધન પૂર્ણાંકનો વર્ગ 5m અથવા 5m ± 1 સ્વરૂપનો હોય.
પાઠ્યપુસ્તકનાં ઉદાહરણો
5. કોઈક ધન પૂર્ણાંક n માટે 4″નો છેલ્લો અંક શૂન્ય હશે કે કેમ તે નિર્ણય કરો.
જો કોઈ પણ પૂર્ણાંક n માટે સંખ્યા 4nનો છેલ્લો અંક શૂન્ય હોય, તો તે 5 વડે વિભાજ્ય હોય. આથી 4nના અવિભાજ્ય અવયવોમાં 5 હોવો જોઈએ. આ શક્ય નથી, કારણ કે 4n = (2)2n. આથી 4nના અવયવીકરણમાં એક જ અવિભાજ્ય પૂર્ણાંક 2 મળે. આથી અંકગણિતના મૂળભૂત પ્રમેયની અનન્યતા શરત અનુસાર નક્કી થાય છે કે 4nના અવયવીકરણમાં 2 સિવાય બીજી કોઈ અવિભાજ્ય સંખ્યા નથી. માટે કોઈ પ્રાકૃતિક સંખ્યા n એવી ન મળે કે જેના માટે 4nનો અંતિમ અંક શૂન્ય હોય.
6. અવિભાજ્ય અવયવીકરણ પદ્ધતિથી 6 અને 20નો ગુ.સા.અ. અને લ.સા.અ. શોધો.

7. 96 અને 404નો ગુ.સા.અ. અવિભાજ્ય અવયવની રીતે મેળવો અને તે પરથી તેનો લ.સા.અ. શોધો.

8. અવિભાજ્ય અવયવોની રીતથી 6, 72 અને 120નો ગુ.સા.અ. અને લ.સા.અ. શોધો.

સ્વાધ્યાય – 1.2
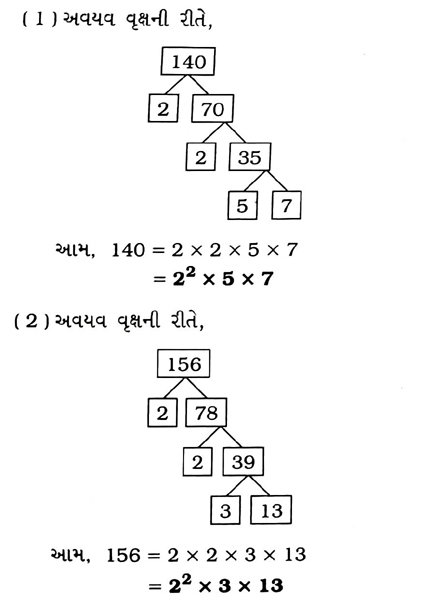
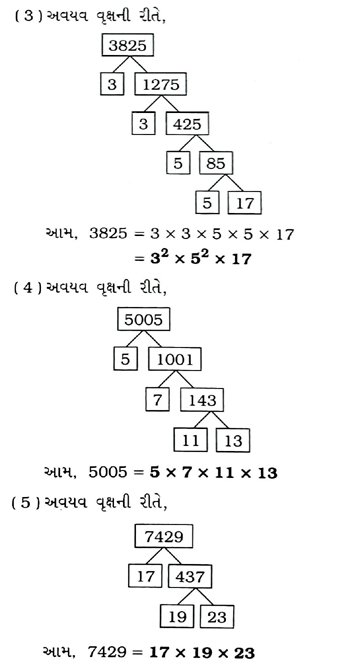
1. નીચેની દરેક સંખ્યાને તેના અવિભાજ્ય અવયવોના ગુણાકાર સ્વરૂપે દર્શાવો :
(1) 140 (2) 156 (3) 3825 (4) 5005 (5) 7429
2. નીચે આપેલ પૂર્ણાંકોની જોડીના ગુ.સા.અ. અને લ.સા.અ. શોધો અને ગુ.સા.અ. × લ.સા.અ. = બંને પૂર્ણાંકોનો ગુણાકાર થાય છે તેમ ચકાસો :
(1) 26 અને 91 (2) 510 અને 92 (3) 336 અને 54

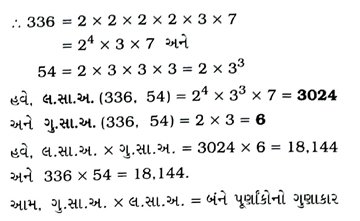
૩. નીચે આપેલ પૂર્ણાંકોના અવિભાજ્ય અવયવની રીતે ગુ.સા.અ. અને લ.સા.અ. શોધો :
(1) 12, 15 અને 21 (2) 17, 23 અને 29 (3) 8, 9 અને 25

4. જો ગુ.સા.અ. (306, 657) = 9 આપેલ હોય, તો લ.સા.અ. (306, 657) શોધો.


5. કોઈક પ્રાકૃતિક સંખ્યા n માટે 6નો અંતિમ અંક શૂન્ય થાય કે નહીં તે ચકાસો.
જો કોઈ સંખ્યાનો અંતિમ અંક 0 હોય, તો તે સંખ્યા 5 તેમજ 2 બંને વડે વિભાજ્ય હોય. એટલે કે, અંતિમ અંક 0 હોય તેવી સંખ્યાના અવિભાજ્ય અવયવીકરણમાં 5 તેમજ 2 બંનેનો સમાવેશ થાય.
હવે, 6n = (2 × 3)n = 2n × 3n, જ્યાં n કોઈ પ્રાકૃતિક સંખ્યા છે. આમ, 6nને 2 અને 3 એમ ફક્ત બે જ અવિભાજ્ય અવયવો છે. આમ, 6nના અવિભાજ્ય અવયવીકરણમાં 5નો સમાવેશ થતો ન હોવાથી કોઈક પ્રાકૃતિક સંખ્યા n માટે 6nનો અંતિમ અંક 0 ન જ થાય.
6. સમજાવો કે, 7 × 11 × 13 + 13 અને
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 એ શા માટે વિભાજ્ય સંખ્યાઓ છે?


7. એક રમતના મેદાનમાં વર્તુળાકાર માર્ગ છે. સોનિયાને તેનું એક પરિભ્રમણ પૂર્ણ કરતાં 18 મિનિટ લાગે છે, જ્યારે રવિને તેનું એક પરિભ્રમણ પૂર્ણ કરતાં 12 મિનિટ લાગે છે. ધારો કે બંને એક જ સમયે, એક જ બિંદુએથી, એક જ દિશામાં પરિભ્રમણ કરવાનું પ્રારંભ કરે છે, તો કેટલી મિનિટ બાદ બંને ફરી પ્રારંભબિંદુ પર ભેગા થાય?
અહીં, સોનિયાને અને રવિને એક પરિભ્રમણ પૂર્ણ કરતાં લાગતા સમય(મિનિટમાં)નો લ.સા.અ. એ આપેલ પ્રશ્નનો જવાબ થાય.
હવે, 12 = 2 × 2 × 3 = 22 × 3 અને
18 = 2 × 3 × 3 = 2 × 3 × 32
માટે, લ.સા.અ. (12, 18) = 22 × 32 = 36
આથી જો સોનિયા અને રવિ એક જ સમયે, એક જ બિંદુએથી, એક જ દિશામાં પરિભ્રમણ કરવાનું પ્રારંભ કરે, તો 36 મિનિટ, બાદ બંને ફરી પ્રારંભબિંદુ પર ભેગા થાય.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. યુક્લિડની ભાગપ્રવિધિ દ્વારા 660 અને 252નો ગુ.સા.અ. શોધો તેમજ અવિભાજ્ય અવયવીકરણની રીતે તેની ચકાસણી કરો.
660 અને 252 માટે, 660 > 252.
∴ 660 = 252 × 2 + 156
શેષ ≠ 0 હોવાથી આપણે 252 અને 156 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
252 = 156 × 1 + 96
શેષ ≠ 0 હોવાથી આપણે 156 અને 96 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
156 = 96 × 1 + 60
શેષ ≠ 0 હોવાથી આપણે 96 અને 60 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
96 = 60 × 1 + 36
શેષ ± 0 હોવાથી આપણે 60 અને 36 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
60 = 36 × 1 + 24
શેષ ≠ 0 હોવાથી આપણે 36 અને 24 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
36 = 24 × 1 + 12
શેષ ≠ 0 હોવાથી આપણે 24 અને 12 પર ભાગપ્રવિધિનો ઉપયોગ કરીશું.
24 = 12 × 2 + 0
શેષ = 0 હોવાથી ભાજક 12 એ માગેલ ગુ.સા.અ. છે.
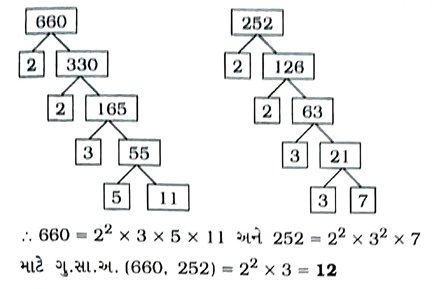
∴ ગુ.સા.અ. (660, 252) = 12
અવિભાજ્ય અવયવીકરણની રીતે :
અવયવ વૃક્ષની રીતે,
2 અવિભાજ્ય અવયવીકરણની રીતે 315 અને 1275નો ગુ.સા.અ. શોધો. ત્યારબાદ ગુ.સા.અ., લ.સા.અ. અને સંખ્યાઓ વચ્ચેના સંબંધ દ્વારા તેમનો લ.સા.અ. શોધો.
અવયવ વૃક્ષની રીતે,


3. ત્રણ મંદિરના ઘંટ નિયમિત સમયાંતરે ઘંટારવ કરે છે, બે ઘંટારવ વચ્ચેનો સમયગાળો પહેલા મંદિર માટે 8 મિનિટ, બીજા મંદિર માટે 12 મિનિટ અને ત્રીજા મંદિર માટે 15 મિનિટ છે. જો તેઓ ત્રણેય કોઈ સમયે એકસાથે ઘંટારવ કરે, તો કેટલા સમય બાદ તે ત્રણેય ફરીથી એકસાથે ઘંટારવ કરશે તે શોધો.
ત્રણેય મંદિરના ઘંટ એકસાથે ઘંટારવ કરે તેવા બે પ્રસંગો વચ્ચેનો સમયગાળો તે દરેકના બે ઘંટારવ વચ્ચેના સમયગાળાના લ.સા.અ. દ્વારા મળે, એટલે કે 8 મિનિટ, 12 મિનિટ અને 15 મિનિટના લ.સા.અ. જૈટલા સમય બાદ ત્રણેય ઘંટ એકસાથે ઘંટારવ કરે. એટલે કે આપણે 8, 12 અને 15નો લ.સા.અ. શોધવો જોઈએ.
8 = 2 × 2 × 2 = 23, 12 = 2 × 2 × 3 = 22 × 3 અને 15 = 3 × 5.
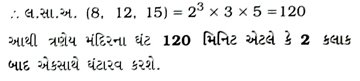
કૌશલ્ય ચકાસણી
1. નીચેના અવયવ વૃક્ષ પરથી a, b, c અને તની કિંમતો શોધો :
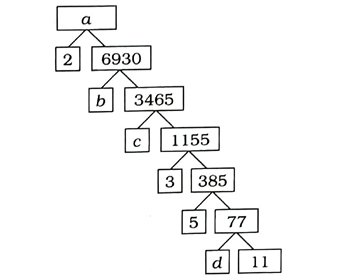
જવાબ: a = 13,860, b = 2, c = 3, d = 7
2. અવિભાજ્ય અવયવીકરણની રીતે 525 અને 1120નો ગુ.સા.અ. શોધો. ત્યારબાદ લ.સા.અ., ગુ.સા.અ. અને સંખ્યાઓ વચ્ચેના સંબંધ પરથી તેઓનો લ.સા.અ. શોધો.
જવાબ: ગુ.સા.અ. = 35, લ.સા.અ. = 16,800
3. 128 અને 68ના ગુ.સા.અ.ને 128m – 15 × 68 સ્વરૂપે રજૂ કરી શકાતો હોય, તો mની કિંમત શોધો. ત્યારબાદ અવિભાજ્ય અવયવીકરણની રીતે 128 અને 68નો લ.સા.અ. શોધો.
જવાબ: ગુ.સા.અ. = 4, m = 8, લ.સા.અ. = 2176
4. તૃષા, રમીઝ અને ખુશ ક્રીમ વિલેજના વર્તુળાકાર મેદાનમાં પરિભ્રમણ કરે છે. તૃષાને એક પરિભ્રમણ પૂર્ણ કરતાં 9 મિનિટ, રમીઝને એક પરિભ્રમણ પૂર્ણ કરતાં 12 મિનિટ અને ખુશને તેનું એક પરિભ્રમણ પૂર્ણ કરતાં 15 મિનિટ લાગે છે. ધારો કે ત્રણેય એક જ સમયે એક જ બિંદુથી એક જ દિશામાં પરિભ્રમણ કરવાનું આરંભે છે, તો કેટલી મિનિટ બાદ ત્રણેય ફરી પ્રારંભબિંદુ પર ભેગા થાય?
જવાબ: 180 મિનિટ
5. બે સંખ્યાઓનો ગુ.સા.અ. 145 અને તેઓનો લ.સા.અ. 2175 છે. જો તે સંખ્યાઓ પૈકી એક સંખ્યા 725 હોય, તો બીજી સંખ્યા શોધો.
જવાબ: 435
6. 510 અને 92 નો ગુ.સા.અ. તેમજ લ.સા.અ. શોધો અને ચકાસો કે, ગુ.સા.અ. × લ.સા.અ. = બે સંખ્યાઓનો ગુણાકાર.
જવાબ: ગુ.સા.અ. = 2, લ.સા.અ. = 23,460
7. 60, 120 અને 288નો ગુ.સા.અ. તેમજ લ.સા.અ. શોધો.
જવાબ: ગુ.સા.અ. = 12, લ.સા.અ. = 1440
પાઠ્યપુસ્તકનાં ઉદાહરણો
9. સાબિત કરો કે, √3 એ અસંમેય છે.
શક્ય હોય તો ધારો કે, √3 એ સંમેય છે.
આથી આપણે શૂન્યેતર પૂર્ણાંક a અને b શોધી શકીએ કે જેથી √3 = a/b થાય. (b ≠ 0)
ધારો કે, a અને b ને 1 સિવાય કોઈ સામાન્ય અવયવ છે.
આથી આપણે તેને સામાન્ય અવયવ વડે ભાગી શકીએ અને વ્યાપકતા ગુમાવ્યા સિવાય માની શકીએ કે a અને b પરસ્પર અવિભાજ્ય છે.
આથી b/3 = a.
બંને બાજુ વર્ગ કરી પુનઃગોઠવણ કરતાં આપણને 3b2 = a2 મળે.
માટે a2 એ 3 વડે વિભાજ્ય છે અને આથી પ્રમેય 1.3 અનુસાર a પણ 3 વડે વિભાજ્ય છે.
આથી આપણે કોઈ પૂર્ણાંક c માટે a = 3c લખી શકીએ.
a ની કિંમત મૂકવાથી 3b2 = 9c2. આથી આપણને b2 = 3c2 મળે.
આનો અર્થ એ થયો કે b2ને 3 વડે ભાગી શકાય અને તેથી b ને પણ 3 વડે ભાગી શકાય. (p = 3 માટે પ્રમેય 1.3નો ઉપયોગ કરતાં)
આથી a તથા bને ઓછામાં ઓછો એક સામાન્ય અવયવ 3 છે.
માટે a અને b પરસ્પર અવિભાજ્ય હોવાના વિધાનનો વિરોધાભાસ ઊભો થયો.
આ વિરોધાભાસ ઉદ્ભવ્યો, કારણ કે આપણે ‘ √૩ સંમેય છે.’ કરેલ ધારણા અસત્ય છે.
માટે આપણે કહી શકીએ કે, √૩ એ અસંમેય છે.
10. દર્શાવો કે, 5 – √3 અસંમેય છે.
ધારો કે, 5 – √3 એ સંમેય છે.
આથી આપણે પરસ્પર અવિભાજ્ય પૂર્ણાંક a અને શૂન્યેતર પૂર્ણાંક b શોધી શકીએ કે, જેથી 5 – √3 = a/b થાય.

11. દર્શાવો કે, 3√2 અસંમેય છે.

સ્વાધ્યાય – 1.3
1. સાબિત કરો કે, √5 અસંમેય છે.
ધારો કે, √5 સંમેય સંખ્યા છે.
આથી આપણને પરસ્પર અવિભાજ્ય પૂર્ણાંકો a અને b એવા મળે જેથી √5 = a/b થાય.
બંને બાજુનો વર્ગ કરતાં,
5 = a2/b2
∴ a2 = 5b2
આમ, 5 એ a2નો અવયવ છે.
પરંતુ 5 એ અવિભાજ્ય હોવાથી, પ્રમેય 1.3 મુજબ 5 એ a નો પણ અવયવ છે.
ધારો કે, a = 5c જ્યાં, c કોઈ પૂર્ણાંક છે.
∴ a2 = 25c2
∴ 25c2 = 5b2
∴ b2 = 5c2
આમ, 5 એ b2નો અવયવ છે.
પરંતુ 5 એ અવિભાજ્ય હોવાથી, પ્રમેય 1.3 મુજબ 5 એ bનો પણ અવયવ છે.
આમ, a અને bનો સામાન્ય અવયવ 5 છે.
પરંતુ આ વિધાન એ a અને b પરસ્પર અવિભાજ્ય છે તે ધારણાથી વિરુદ્ધ છે.
માટે આપણી ધારણા છે કે ‘ √5 સંમેય સંખ્યા છે.’ તે ખોટી છે. આથી સાબિત થાય છે કે √5 અસંમેય છે.
2. સાબિત કરો કે, 3 + 2√5 અસંમેય છે.
ધારો કે, 3 + 2√5 સંમેય છે.

૩. નીચે દર્શાવેલ સંખ્યાઓ અસંમેય છે તેમ સાબિત કરો :


મહત્ત્વનાં અન્ય ઉદાહરણો


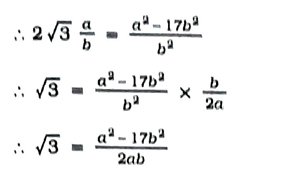

સ્વાધ્યાય – 1.4
1. ભાગાકારની લાંબી પ્રક્રિયા કર્યા વગર, નીચે દર્શાવેલ સંમેય સંખ્યાઓનું દશાંશ નિરૂપણ સાન્ત છે કે અનંત અને આવૃત્ત છે તે જણાવો :


2. પ્રશ્ન 1માં જે સંમેય સંખ્યાઓનું દશાંશ નિરૂપણ સાન્ત હોય તેનું દશાંશ નિરૂપણ દર્શાવો.

3. નીચેની વાસ્તવિક સંખ્યાઓનું દશાંશ નિરૂપણ દર્શાવેલ છે. દરેક માટે જણાવો કે તે સંમેય છે કે નહીં. અને જો સંમેય હોય, તો તેના p/q સ્વરૂપમાં qના અવિભાજ્ય અવયવો વિશે તમે શું કહી શકશો?
(1) 43.123456789
(2) 0.120120012000120000 …
(3) 43.123456789
(1) આપેલ સંખ્યા 43.123456789નું દશાંશ નિરૂપણ સાન્ત હોવાથી તે સંમેય સંખ્યા છે.
આપેલ સંખ્યાનું દશાંશ નિરૂપણ સાન્ત હોવાથી તેના p/q સ્વરૂપમાં છેદના અવિભાજ્ય અવયવો ફક્ત 2 અથવા 5 અથવા બંને હોય. (પ્રમેય 1.5)
(2) આપેલ સંખ્યા 0.120120012000120000 …નું દશાંશ નિરૂપણ અનંત અને અનાવૃત્ત હોવાથી તે અસંમેય સંખ્યા છે.
(3) આપેલ સંખ્યા 43.123456789 નું દશાંશ નિરૂપણ અનંત અને આવૃત્ત હોવાથી તે સંમેય સંખ્યા છે.
આપેલ સંખ્યાનું દશાંશ નિરૂપણ અનંત અને આવૃત્ત હોવાથી તેના p/q સ્વરૂપમાં છેદના અવિભાજ્ય અવયવોમાં 2 અને 5 સિવાયનો ઓછામાં ઓછો એક અવિભાજ્ય અવયવ છે જ. (પ્રમેય 1.7નું પ્રતીપ)
મહત્ત્વનાં અન્ય ઉદાહરણો
1. ભાગાકારની લાંબી પ્રક્રિયા કર્યા વગર, નીચે દર્શાવેલ સંમેય સંખ્યાઓનું દશાંશ નિરૂપણ મેળવો :
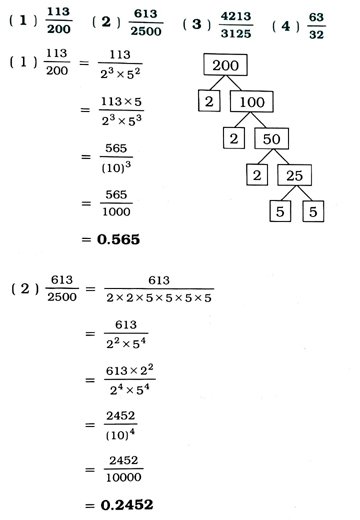

હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
(1) 13211/1250 ના દશાંશ નિરૂપણમાં દશાંશ-સ્થાન બાદ …… અંકો હોય.
(2) ધન પૂર્ણાંકો a અને b માટે a = x3y અને b = x2y3 છે. જ્યાં, x અને y અવિભાજ્ય પૂર્ણાંકો છે. આથી ગુ.સા.અ. (a, b) = ……….
(3) બે ક્રમિક ધન પૂર્ણાંકોનો ગુણાકાર …….. વડે હંમેશાં વિભાજ્ય છે.
(4) ગુ.સા.અ. (156,455) = ………..
(5) લ.સા.અ. (220, 60) = ………..
(6) 23, 35, 46નો લ.સા.અ. ………. થાય છે.
જવાબ : ( 1 ) 4 ( 2 ) x2y ( 3 ) 2 ( 4 ) 13 ( 5 ) 660 ( 6 ) 1610
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
(1) કોઈ પણ ધન પૂર્ણાંક aના વર્ગને 6 વડે ભાગતાં શેષ ……… ન હોઈ શકે.
A. 1
B. 3
C. 4
D. 5
(2) યુક્લિડના ભાગાકારના પૂર્વપ્રમેય અનુસાર ધન પૂર્ણાંક a અને 5 માટે, જો a = 5q + r અનન્ય હોય, તો r = ……… શક્ય નથી.
A. 0
B. 2
C. 6
D. 4
(3) 95 વડે વિભાજ્ય હોય તેવો 4 અંકનો મોટામાં મોટો પૂર્ણાંક છે.
A. 9995
B. 9975
C. 9985
D. 9950
(4) કોઈ પણ અયુગ્મ ધન પૂર્ણાંક તેનું સ્વરૂપ …….. હોય છે. જ્યાં, m કોઈ પૂર્ણાંક છે.
A. 4m + 1 અથવા 4m + 2
B. 4m + 2 અથવા 4m +3
C. 4m + 1 અથવા 4m +3
D. 4m અથવા 4m + 1
(5) નાનામાં નાની અવિભાજ્ય સંખ્યા અને નાનામાં નાની વિભાજ્ય સંખ્યાનો લ.સા.અ. ……… છે.
A. 4
B. 3
C. 2
D. 1
(6) બે ધન પૂર્ણાંકો a અને b માટે, જો
ગુ.સા.અ. (a, b) = 7 અને લ.સા.અ. (a, b) = 385 હોય, તો a × b = ………
A. 385
B. 2695
C. 2595
D. 2675
(7) 98નું અવિભાજ્ય અવયવીકરણ ……. થાય.
A. 22 × 72
B. 2 × 72
C. 22 × 7
D. 2 × 7
(8) નીચે આપેલ અવયવ વૃક્ષ પરથી x અને પુની કિંમતો અનુક્રમે …….. મળે.
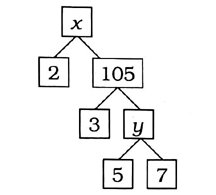
A. 35 અને 210
B. 210 અને 35
C. 200 અને 40
D. 40 અને 200
(9) ………… એ અસંમેય સંખ્યા નથી.
A. √6
B. √5
C. √4
D. √3
(10) જો ગુ.સા.અ. (65, 117) = 65m – 117 હોય, તો m = ………
A. 4
B. 2
C. 1
D. 3
(11) જેના દ્વારા 70 અને 125ને ભાગતાં શેષ અનુક્રમે 5 અને 8 મળે તેવો મોટામાં મોટો ધન પૂર્ણાંક ……. છે.
A. 13
B. 65
C. 875
D. 1750
(12) નીચે આપેલા અવયવ ટ્રી માટે x + y = ………. .
A. 4
B. 20
C. 24
D. 80
જવાબ : ( 1 ) 5 ( 2 ) 6 ( 3 ) 9975 ( 4 ) 4m + 1 અથવા 4m + 3 (5) 4 (6) 2695 ( 7 ) 2 × 72 (8) 210 અને 35 (9) √4 (10) 2 (11) 13 (12) 24
3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ આપો :

જવાબ : (1) b (2) 13 (3) 900 (4) 4 (5) 252
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :

જવાબ : ( 1 ) ખોટું ( 2 ) ખરું ( 3 ) ખોટું ( 4 ) ખોટું ( 5 ) ખરું ( 6 ) ખોટું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here