Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 10 Circles (વર્તુળ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 10 Circles (વર્તુળ)
સ્વાધ્યાય – 10.1
1. વર્તુળને કેટલા સ્પર્શક હોય?
વર્તુળને અસંખ્ય સ્પર્શક હોય. વર્તુળ એ સમતલના એક ચોક્કસ બિંદુ(કેન્દ્ર)થી અચળ અંતરે (ત્રિજ્યા) આવેલાં બિંદુઓનો સમૂહ છે અને વર્તુળના દરેક બિંદુમાંથી વર્તુળને એક સ્પર્શક હોય. આથી વર્તુળને અસંખ્ય સ્પર્શક હોય.
2. ખાલી જગ્યા પૂરોઃ
( 1 ) સ્પર્શક વર્તુળને એક અને માત્ર એક જ બિંદુમાં છેદે.
( 2 ) વર્તુળને બે બિંદુમાં છેદતી રેખાને છેદિકા કહે છે.
( 3 ) વર્તુળની છેદિકાને સમાંતર હોય તેવા વધુમાં વધુ બે સમાંતર સ્પર્શક હોય.
( 4 ) વર્તુળ અને સ્પર્શકના સામાન્ય બિંદુને સ્પર્શબિંદુ કહે છે.
3. 5 સેમી ત્રિજ્યાવાળા વર્તુળના કોઈ બિંદુ P આગળ દોરેલ એક સ્પર્શક PQ, કેન્દ્ર Oમાંથી પસાર થતી રેખાને Q બિંદુએ છેદે છે. OQ = 12 સેમી હોય, તો PQની લંબાઈ …….. હોય.

4. એક વર્તુળ દોરો. વર્તુળના સમતલમાં આપેલી કોઈ એક રેખાને સમાંતર હોય તેવી બે રેખાઓ દોરો, જે પૈકી એક વર્તુળનો સ્પર્શક હોય અને બીજી વર્તુળની છેદિકા હોય.
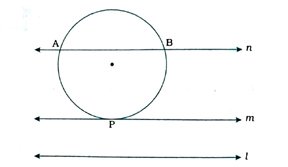
અહીં, રેખા l એ આપેલ રેખા છે તથા રેખા m અને રેખા n એ રેખા lને સમાંતર રેખાઓ છે.
રેખા m એ આપેલ વર્તુળને P બિંદુએ સ્પર્શતો સ્પર્શક છે.
રેખા n એ આપેલ વર્તુળને બિંદુઓ A અને Bમાં છેદતી છેદિકા છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
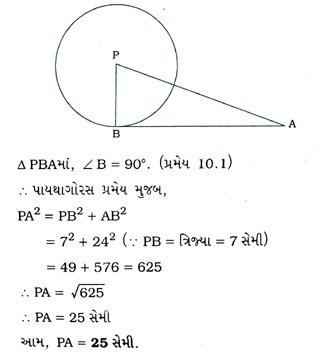
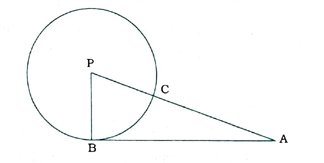
1. P કેન્દ્ર અને 7 સેમી ત્રિજ્યા ધરાવતા વર્તુળના બહારના ભાગમાં આવેલ બિંદુ Aમાંથી દોરેલ સ્પર્શક વર્તુળને B બિંદુમાં સ્પર્શે છે. જો AB = 24 સેમી હોય, તો PA શોધો.
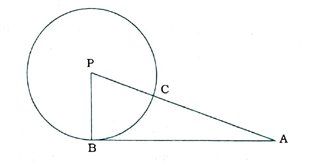
2. AB એ P કેન્દ્રિત વર્તુળનો સ્પર્શક છે. જ્યાં, B એ સ્પર્શબિંદુ છે. PA વર્તુળને C બિંદુમાં છેદે છે. જો AB = 15 સેમી અને AC = 9 સેમી હોય, તો વર્તુળની ત્રિજ્યા શોધો.
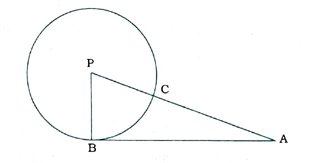
અહીં, AB એ P કેન્દ્રિત વર્તુળનો સ્પર્શક છે. જ્યાં, B એ સ્પર્શબિંદુ છે.
વળી, PA એ વર્તુળને C બિંદુમાં છેદે છે.
આથી PB અને PC એ વર્તુળની ત્રિજ્યાઓ છે.
ધારો કે, PB = PC = r સેમી.
હવે, PA = PC + AC = (r + 9) સેમી.
Δ PBAમાં, ∠ B = 90° (પ્રમેય 10.1)
∴ પાયથાગોરસ પ્રમેય અનુસાર,
PA2 = PB2 + AB2
∴ (r+ 9)² = r² + 152
∴ r² + 18r + 81 = r2 +225
∴ 18r = 144
∴ r = 8
∴ PB = PC = 8 સેમી
આમ, વર્તુળની ત્રિજ્યા 8 સેમી છે.
પાઠ્યપુસ્તકનાં ઉદાહરણો
1. સાબિત કરો કે, બે સમકેન્દ્રી વર્તુળોમાં મોટા વર્તુળની જીવા નાના વર્તુળને સ્પર્શતી હોય, તો સ્પર્શબિંદુ તેને દુભાગે છે.
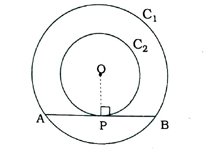
O કેન્દ્રવાળાં બે સમકેન્દ્રીય વર્તુળો C1 અને C2 આપ્યાં છે અને મોટા વર્તુળ C1ની જીવા AB નાના વર્તુળ C2ને બિંદુ Pમાં સ્પર્શે છે. (જુઓ આકૃતિ)
OP જોડો. AB એ C2નો P બિંદુએ સ્પર્શક છે અને OP તેની ત્રિજ્યા છે.
તેથી પ્રમેય 10.1 પરથી, OP ⊥ AB
હવે, AB એ વર્તુળ C1ની જીવા છે અને OP ⊥ AB. તેથી OP એ જીવા ABનો દ્વિભાજક છે, કારણ કે કેન્દ્રમાંથી જીવાને દોરેલો લંબ જીવાને દુભાગે છે.
એટલે કે, AP = BP
આમ, મોટા વર્તુળની જીવા જો નાના વર્તુળને સ્પર્શતી હોય, તો સ્પર્શબિંદુ તે જીવાને દુભાગે છે.
2. O કેન્દ્રવાળા વર્તુળના બહારના બિંદુ Tમાંથી વર્તુળને બે સ્પર્શકો TP અને TQ દોરેલા છે. સાબિત કરો કે, ∠PTQ = 2 ∠OPQ.
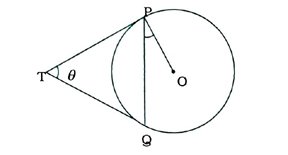
O કેન્દ્રવાળું વર્તુળ, તેની બહારનું બિંદુ T અને વર્તુળના બે સ્પર્શકો TP અને TQ આપેલાં છે. P અને Q સ્પર્શબિંદુઓ છે. (જુઓ આકૃતિ)

3. PQ એ 5 સેમી ત્રિજ્યાવાળા વર્તુળની 8 સેમી લંબાઈની જીવા છે. P અને Qમાંથી પસાર થતા સ્પર્શકો બિંદુ Tમાં છેદે છે. (જુઓ આકૃતિ) TPની લંબાઈ શોધો.
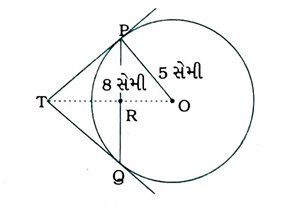
OT જોડો. ધારો કે તે PQને Rમાં છેદે છે.
Δ TPQ સમદ્વિબાજુ છે અને TO એ ∠PTQનો દ્વિભાજક છે. તેથી OT ⊥ PQ અને OT એ PQને દુભાગે છે. તેથી PR = RQ = 4 સેમી.


સ્વાધ્યાય – 10.2
- પ્રશ્ન 1થી 8માં સાચો વિકલ્પ પસંદ કરો અને તે માટે કારણ આપો.
1. બિંદુ ઊમાંથી દોરેલા વર્તુળના સ્પર્શકની લંબાઈ 24 સેમી અને વર્તુળના કેન્દ્રથી તેનું અંતર 25 સેમી હોય, તો વર્તુળની ત્રિજ્યા ……. છે.
(A) 7 સેમી
(B) 12 સેમી
(C) 15 સેમી
(D) 24.5 સેમી
ધારો કે, વર્તુળનું કેન્દ્ર P છે તથા Qમાંથી દોરેલ સ્પર્શકનું સ્પર્શબિંદુ T છે. આથી PT એ સ્પર્શબિંદુમાંથી દોરેલ ત્રિજ્યા થાય તથા PQ = 25 સેમી અને QT = 24 સેમી થાય.

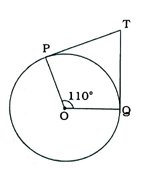
2. આપેલ આકૃતિમાં, જો TP અને TQ એ O કેન્દ્રવાળા વર્તુળના ∠POQ = 110° બને એવા સ્પર્શકો છે, તો ∠PTQ = ……… છે.
(A) 60°
(B) 70°
(C) 80°
(D) 90°
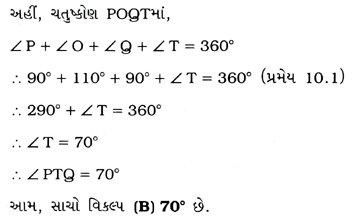
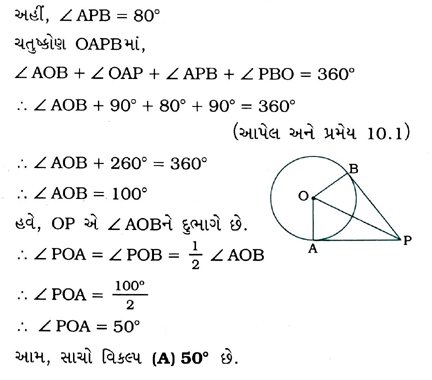
3. જો O કેન્દ્રવાળા વર્તુળને બિંદુ માાંથી દોરેલા સ્પર્શકો PA અને PB વચ્ચે 80°નો ખૂણો રચાતો હોય, તો ∠POA = …… છે.
(A) 50°
(B) 60°
(C) 70°
(D) 80°
4. સાબિત કરો કે, વર્તુળના વ્યાસના અંત્યબિંદુઓએ દોરેલા સ્પર્શકો પરસ્પર સમાંતર હોય છે.
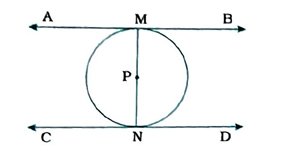
પક્ષ : P કેન્દ્રવાળા વર્તુળમાં MN વ્યાસ છે. AB અને CD એ વર્તુળના સ્પર્શક છે, જે વર્તુળને અનુક્રમે M અને Nમાં સ્પર્શે છે.
સાધ્ય : AB || CD
સાબિતી : AB એ વર્તુળને M બિંદુએ સ્પર્શક છે અને PM એ સ્પર્શબિંદુ Mમાંથી દોરેલ ત્રિજ્યા છે.

5. સાબિત કરો કે, વર્તુળના સ્પર્શકના સ્પર્શબિંદુમાંથી દોરેલો લંબ વર્તુળના કેન્દ્રમાંથી પસાર થાય છે.
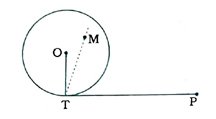
અહીં, PT એ O કેન્દ્રવાળા વર્તુળને T બિંદુમાં સ્પર્શતો સ્પર્શક છે અને બિંદુ M વર્તુળના અંદરના ભાગનું એવું બિંદુ છે, જેથી MT ⊥ PT થાય.
ધારો કે, TM એ કેન્દ્ર Oમાંથી પસાર નથી થતી.
હવે, ∠MTP = 90° (‘.’ MT ⊥ PT)
વળી, ∠OTP = 90° (પ્રમેય 10.1)
∴ ∠MTP = ∠OTP
આ ત્યારે જ શક્ય થાય જ્યારે OT અને MT સંપાતી હોય. આથી MT કેન્દ્ર Oમાંથી પસાર થાય છે. આમ, વર્તુળના સ્પર્શકના સ્પર્શબિંદુમાંથી દોરેલો લંબ વર્તુળના કેન્દ્રમાંથી પસાર થાય છે.
6. વર્તુળના કેન્દ્રથી 5 સેમી અંતરે આવેલા બિંદુ Aથી દોરેલા સ્પર્શકની લંબાઈ 4 સેમી છે. વર્તુળની ત્રિજ્યા શોધો.

7. બે સમકેન્દ્રી વર્તુળોની ત્રિજ્યાઓ 5 સેમી અને 3 સેમી છે. મોટા વર્તુળની જીવા નાના વર્તુળને સ્પર્શે છે, તો તેની લંબાઈ શોધો.

આમ, મોટા વર્તુળની જીવા કે જે નાના વર્તુળને સ્પર્શે છે તેની લંબાઈ 8 સેમી છે.
8. ચતુષ્કોણ ABCD એક વર્તુળને પરિગત છે. (જુઓ આકૃતિ) સાબિત કરો કે, AB + CD = AD + BC.
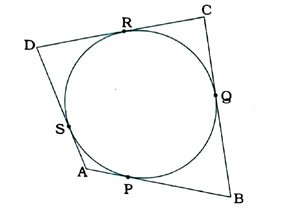
પ્રમેય 10.2 મુજબ વર્તુળની બહારના બિંદુમાંથી દોરેલા સ્પર્શકોની લંબાઈ સમાન હોય છે. આથી

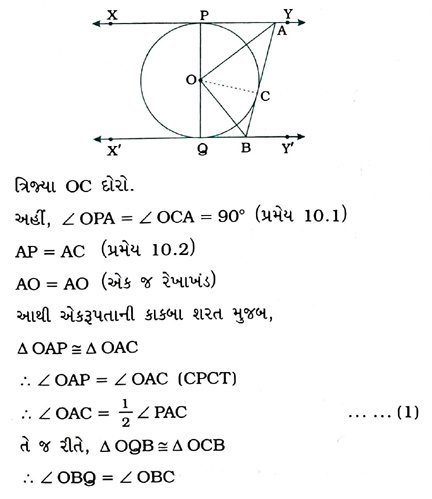
9. આપેલ આકૃતિમાં, O કેન્દ્રવાળા વર્તુળના બે સ્પર્શકો XY અને X’Y’ સમાંતર છે અને વર્તુળ પરના સ્પર્શબિંદુ C આગળ દોરેલો ત્રીજો સ્પર્શક XYને A બિંદુએ અને X’Y’ને B બિંદુએ છેદે છે. સાબિત કરો કે, ∠AOB = 90°.

10. સાબિત કરો કે, વર્તુળની બહારના બિંદુમાંથી વર્તુળને દોરેલા બે સ્પર્શકો વચ્ચેનો ખૂણો અને સ્પર્શબિંદુઓને કેન્દ્રને જોડતા રેખાખંડ વચ્ચેનો ખૂણો એકબીજાને પૂરક હોય છે.
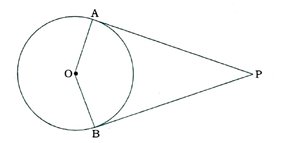
પક્ષ : બિંદુ P એ O કેન્દ્રિત વર્તુળના બહારના ભાગનું બિંદુ છે તથા Pમાંથી દોરેલા સ્પર્શકો PA અને PB વર્તુળને અનુક્રમે A અને Bમાં સ્પર્શે છે.
સાધ્ય : ∠APB + ∠AOB = 180°

11. સાબિત કરો કે, વર્તુળને પરિગત સમાંતરબાજ઼ ચતુષ્કોણ સમબાજુ ચતુષ્કોણ છે.
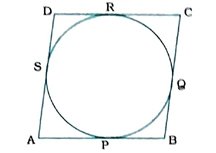
અહીં, ABCD એ એક વર્તુળને પરિગત સમાંતરબાજુ ચતુષ્કોણ છે, જેની બાજુઓ AB, BC, CD અને DA વર્તુળને અનુક્રમે P, Q, R અને Sમાં સ્પર્શે છે.

આમ, સમાંતરબાજુ ચતુષ્કોણ ABCDની પાસપાસેની બાજુઓ AB અને BC સમાન છે.
આથી સમાંતરબાજુ ચતુષ્કોણ ABCDની બધી જ બાજુઓ સમાન છે.
આથી સમાંતરબાજુ ચતુષ્કોણ ABCD એ સમબાજુ ચતુષ્કોણ છે.
12. ત્રિકોણ ABC એ 4 સેમી ત્રિજ્યાવાળા વર્તુળને પરિગત છે. રેખાખંડ BD અને DC એ BCનું સ્પર્શબિંદુ D આગળ અનુક્રમે 8 સેમી અને 6 સેમી લંબાઈના રેખાખંડમાં વિભાજન કરે છે. (જુઓ આકૃતિ) બાજુઓ AB અને AC શોધો.
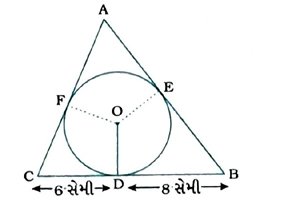
ધારો કે, AB અને AC એ ΔABCના અંતઃવૃત્તને અનુક્રમે E અને Fમાં સ્પર્શે છે.

13. સાબિત કરો કે, વર્તુળને પરિગત ચતુષ્કોણની સામસામેની બાજુઓથી વર્તુળના કેન્દ્ર આગળ રચાતા ખૂણાઓ પૂરક હોય છે.


આમ, વર્તુળને પરિગત ચતુષ્કોણની સામસામેની બાજુઓથી વર્તુળના કેન્દ્ર આગળ રચાતા ખૂણાઓ પૂરક હોય છે.
મહત્ત્વનાં અન્ય ઉદાહ૨ણો
1. સાબિત કરો કે, વર્તુળની કોઈ જીવાના અંત્યબિંદુએ વર્તુળને સ્પર્શતા સ્પર્શકો જીવા સાથે સમાન ખૂણા બનાવે છે.
ધારો કે, AB એ O કેન્દ્રિત વર્તુળની જીવા છે તથા A અને B બિંદુમાં સ્પર્શતા સ્પર્શકો બિંદુ Pમાં છેદે છે.
આથી પ્રમેય 10.2 મુજબ, PA = PB
હવે, Δ PABમાં, PA = PB
∴ ∠PAB = ∠PBA
આમ, વર્તુળની કોઈ જીવાના અંત્યબિંદુએ વર્તુળને સ્પર્શતા સ્પર્શકો જીવા સાથે સમાન ખૂણા બનાવે છે.
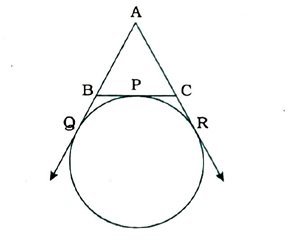
2. એક વર્તુળ Δ ABCની બાજુ BCને P બિંદુમાં સ્પર્શે છે તથા લંબાવેલ AB અને લંબાવેલ ACને અનુક્રમે Q અને Rમાં સ્પર્શે છે. સાબિત કરો કે, AQ = 1/2 (Δ ABCની પરિમિતિ).

3. આપેલ આકૃતિમાં, A અને B કેન્દ્રવાળાં વર્તુળો બહારથી C બિંદુએ સ્પર્શે છે. સાબિત કરો કે, C બિંદુમાંથી પસાર થતો સામાન્ય સ્પર્શક બે વર્તુળોને P અને Q બિંદુએ સ્પર્શતા સામાન્ય સ્પર્શકને દુભાગે છે.
ધારો કે, C બિંદુમાંથી પસાર થતો સામાન્ય સ્પર્શક P અને Q બિંદુઓમાં સ્પર્શતા સામાન્ય સ્પર્શકને R બિંદુમાં છેદે છે.
પ્રમેય 10.2 મુજબ, વર્તુળના બહારના ભાગમાં આવેલ બિંદુમાંથી દોરેલા સ્પર્શકો સમાન હોય છે.
∴ RP = RC અને RC = RQ
∴ RP = RQ
∴ R એ PQનું મધ્યબિંદુ છે.
આમ, C બિંદુએ સ્પર્શતો સામાન્ય સ્પર્શક P અને Q બિંદુઓમાં સ્પર્શતા સામાન્ય સ્પર્શકને દુભાગે છે.
4. એક કાટકોણ ત્રિકોણની બાજુઓની લંબાઈ a, b અને c છે, જેમાં c કર્ણ છે. સાબિત કરો કે, ત્રિકોણની ત્રણેય બાજુઓને સ્પર્શતા વર્તુળની ત્રિજ્યા r = a+b-c/2 દ્વારા મળે.
અહીં, Δ ABCમાં ∠C કાટખૂણો છે તથા તેનું અતઃવૃત્ત BC, CA અને ABને અનુક્રમે D, E અને Fમાં સ્પર્શે છે.
આથી પ્રમેય 10.2 મુજબ, AE = AF; BF = BD અને CD = CE.

5. O કેન્દ્ર અને 5 સેમી ત્રિજ્યાવાળા એક વર્તુળમાં જીવા PQની લંબાઈ 8 સેમી છે. P અને Q પરના સ્પર્શકો T બિંદુમાં છેદે છે. TPની લંબાઈ શોધો.

6. આપેલ આકૃતિમાં, AB અને CD એ O1 અને O2 કેન્દ્રો ધરાવતાં બે અસમાન વર્તુળોના સામાન્ય સ્પર્શકો છે. સાબિત કરો કે, AB = CD.
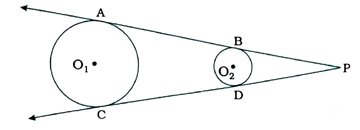
O1 અને O2 કેન્દ્રો ધરાવતાં વર્તુળો અસમાન હોવાથી તેઓના સામાન્ય સ્પર્શક AB અને CD સમાંતર નથી.
ધારો કે, લંબાવેલ AB અને લંબાવેલ CD પરસ્પર P બિંદુમાં છેદે છે.
પ્રમેય 10.2 મુજબ, વર્તુળની બહારના બિંદુમાંથી દોરેલા સ્પર્શકોની લંબાઈ સમાન હોય છે.
આથી O1 કેન્દ્રવાળા વર્તુળ માટે PA = PC અને O2 કેન્દ્રવાળા વર્તુળ માટે PB = PD.
હવે, PA – PB = PC – PD
∴ AB = CD
હેતુલક્ષી પ્રશ્નોતર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધર્મોમાં ખાલી જગ્યા પૂરો :
( 1 ) એક વર્તુળની બહારના બિંદુ ઊમાંથી દોરેલ સ્પર્શકની લંબાઇ 24 સેમી અને બિંદુ ઊનું વર્તુળના કેન્દ્રથી અંતર 25 સેમી છે, તો તે વર્તુળની ત્રિજ્યા ……… સેમી હોય,
( 2 ) O કેન્દ્રિત વર્તુળને બાઘબિંદુ Pમાંથી દોરેલ સ્પર્શકો PA અને PB વચ્ચેના ખુણામાં માપ 80° હોય, તો ∠POA = ……..
( 3 ) O કેન્દ્રિત વર્તુળના બિંદુ Pમાંથી ઘેરૈલ સ્પર્શક PQ છે, જો ΔOPQ સમતિભુજ ત્રિશ્રેણ હોય, તો ∠OQP = ……..
( 4 ) બે સમાન વર્તુળો પરસ્પર C બિંદુએ બહારથી સ્પર્શે છે. જો AB એ તેમનો સામાન્ય સ્પર્શક હોય, તો ∠ACB = ………
( 5 ) ચતુષ્કોલ ABCD એક વર્તુળનું પગિત છે. જ AB = 7.2 સેમી, BC = 8.5 સેમી અને DA = 6.9 સેમી હોય, તો CD = ……. સમી,
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
( 1 ) O કેન્દ્રિત વર્તુળના સ્પર્શક PQનું સ્પર્શબિંદુ Q છે તથા QR એ વર્તુળનો વ્યાસ છે, જો ∠POR = 120° હોય, તો ∠OPQ = ……….
A. 60°
B, 45°
C. 30°
D. 90°
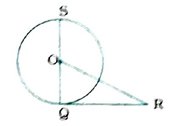
( 2 ) આપેલ. આકૃતિમાં, RQ એ O કેન્દ્રિત વર્તુળનો સ્પર્શક છે. જો SQ = 6 ર્ચમી અને QR = 4 સેમી હોય, તો OR = ……. સેમી.
A. 8
B. 3
C. 2.5
D. 5
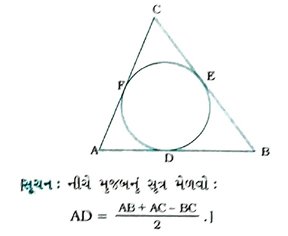
( 3 ) આપેલ આકૃતિમાં, જો AB = 12 સેમી BC = 8 સેમી અને AC = 10 સેમી, તો AD = …….. સેમી.
A. 5
B. 4
C. 6
D. 7
( 4 ) O કેન્દ્ર અને 9 સેમી ત્રિજ્યાવાળા વર્તુળની બહારના ભાગમાં રહેલ બિંદુ Aમાંથી દોરેલા સ્પર્શકો AP અને AQ વર્તુળને P અને Q બિંદુએ સ્પર્શે છે. જો OA = 15 સેમી હોય, તો AP + AQ =……… સેમી.
A. 12
B. 18
C. 24
D, 36
( 5 ) 5 સેમી ત્રિજ્યાવાળા વર્તુળના વ્યાસ ABના અંત્યબિંદુ Aમાંથી વર્તુળને સ્પર્શક XAY દોરેલ છે. વર્તુળની એક જીવા CD એ Aથી 8 સેમી અંતરે છે અને XYને સમાંતર છે. આથી CDની લંબાઈ ……. સેમી થાય.
A. 4
B. 5
C. 6
D. 8
( 6 ) 3 સેમી ત્રિજ્યાવાળા વર્તુળને દોરેલ બે સ્પર્શકો વચ્ચેનો ખૂણો 60નો હોય, તો તે દરેક સ્પર્શકની લંબાઈ ……… સેમી હોય.
A. 3√3/2
B. 6
C. 3
D. 3√3
( 7 ) Δ ABCમાં, ∠B = 90°, BC = 12 સેમી અને AB = 5 સેમી છે, તો ΔABCના અંતઃવૃત્તની ત્રિજ્યા …….. સેમી થાય.
A. 4
B. 3
C. 2
D. 1
( 8 ) જો કોઈ વર્તુળની બે ત્રિજ્યાઓ વચ્ચેનો ખૂણો 130°નો હોય, તો તે બે ત્રિજ્યાઓના અંત્યબિંદુએ દોરેલા બે સ્પર્શકો વચ્ચેનો ખૂણો ……… નો હોય.
A, 90°
B. 50°
C. 70°
D. 40°
( 9 ) બે સમકેન્દ્રીય વર્તુળોની ત્રિજ્યા 17 સેમી અને 15 સેમી છે, તો મોટા વર્તુળની કોઈ પણ જીવા જે નાના વર્તુળનો સ્પર્શક થાય તેની લંબાઈ …….. સેમી હોય.
A. 8
B. 12
C. 16
D. 20
( 10 ) O કેન્દ્રિત વર્તુળને દોરેલા બે સ્પર્શકો AP અને AQ પરસ્પર લંબ છે અને દરેક સ્પર્શકની લંબાઈ 5 સેમી છે, તો તે વર્તુળની ત્રિજ્યા ……. સેમી હોય.
A. 10
B. 7.5
C. 5
D. 2.5
3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ લખો :
( 1 ) બે વર્તુળોના કેન્દ્ર O તથા O’ છે અને તેમની ત્રિજ્યા 7 સેમી અને 10 સેમી છે. જો તેમનાં કેન્દ્રો વચ્ચેનું અંતર 12 સેમી હોય, તો તે વર્તુળો કેટલાં બિંદુમાં છેદે?
( 2 ) જે ત્રિકોણની બાજુઓ 12 સેમી, 35 સેમી અને 37 સેમી હોય તેના અંતઃવૃત્તની ત્રિજ્યા કેટલી હોય ?
( 3 ) O કેન્દ્રિત વર્તુળના બે સ્પર્શકો PA અને PB વચ્ચેનો ખૂણો 70°નો હોય, તો ∠OABકેટલાનો હોય ?
( 4 ) એક વર્તુળ ચતુષ્કોણ PQRSમાં અંતર્ગત છે. જો PQ = 5 સેમી, QR = 8.2 સેમી અને RS = 9.3 સેમી હોય, તો SPની લંબાઈ કેટલી હોય?
( 5 ) બે સમકેન્દ્રીય વર્તુળોની ત્રિજ્યા 40 સેમી અને 41 સેમી છે. મોટા વર્તુળની એવી જીવા કે જે નાના વર્તુળને સ્પર્શતી હોય તેની લંબાઈ કેટલી હોય?
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) બે વર્તુળોને ઓછામાં ઓછો એક સામાન્ય સ્પર્શક હોય.
( 2 ) બે વર્તુળોના કેન્દ્ર O તથા O’ છે અને તેમની ત્રિજ્યાઓ 7 સેમી અને 9 સેમી છે. જો OO’ = 20 સેમી હોય, તો તે વર્તુળોને ચાર સામાન્ય સ્પર્શકો હોય.
( 3 ) વર્તુળને પરિગત હોય તેવો લંબચોરસ ચોરસ હોય.
( 4 ) ચતુષ્કોણ ABCD એક વર્તુળને પરિગત છે. જો ABCDમાં AB સૌથી લાંબી બાજુ હોય, તો CD સૌથી ટૂંકી બાજુ થાય.
( 5 ) એક વર્તુળનો વ્યાસ 20 સેમી છે, આથી તેના દરેક સ્પર્શકની લંબાઈ 20 સેમીથી ઓછી હોય.
( 6 ) વર્તુળના સ્પર્શકના સ્પર્શબિંદુમાંથી દોરેલો લંબ વર્તુળના કેન્દ્રમાંથી પસાર થાય છે.
( 7 ) વર્તુળના આપેલા વ્યાસને સમાંતર વધુમાં વધુ બે સ્પર્શકો દોરી શકાય.
5. વ્યાખ્યા લખો :
( 1 ) વર્તુળની જીવા
( 2 ) વર્તુળની છેદિકા
( 3 ) વર્તુળનો સ્પર્શક
( 4 ) વર્તુળના સ્પર્શકનું સ્પર્શબિંદુ
( 5 ) સામાન્ય સ્પર્શક
( 6 ) બાહ્ય સામાન્ય સ્પર્શક
( 7 ) આંતરિક સામાન્ય સ્પર્શક
( 8 ) ત્રિકોણનું અંતઃવૃત્ત તથા અંતઃત્રિજ્યા
જવાબ :
1. ( 1 ) 7 ( 2 ) 50° ( 3 ) 45° ( 4 ) 90° ( 5 ) 8.2
2. ( 1 ) 30° ( 2 ) 5 ( 3 ) 7 ( 4 ) 24 ( 5 ) 8 ( 6 ) 3√3 ( 7 ) 2 ( 8 ) 50° ( 9 ) 16 ( 10 ) 5
3. ( 1 ) 2 બિંદુઓમાં ( 2 ) 5 સેમી ( 3 ) 35° ( 4 ) 6. 1 સેમી ( 5 ) 18 સેમી
4. ( 1 ) ખોટું ( 2 ) ખરું ( 3 ) ખરું ( 4 ) ખરું ( 5 ) ખોટું ( 6 ) ખરું ( 7 ) ખોટું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here