Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 12 Areas Related to Circles (વર્તુળ સંબંધિત ક્ષેત્રફળ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 12 Areas Related to Circles (વર્તુળ સંબંધિત ક્ષેત્રફળ)
સ્વાધ્યાય – 12.1
1. બે વર્તુળની ત્રિજ્યા 19 સેમી અને 9 સેમી છે. જે વર્તુળનો પરિઘ આ બે વર્તુળના પરિઘના સરવાળા જેટલો હોય, તે વર્તુળની ત્રિજ્યા શોધો.
અહીં, આપેલ બે વર્તુળોની ત્રિજ્યા r1 = 19 સેમી અને r2 = 9 સેમી છે.

2. બે વર્તુળની ત્રિજ્યા 8 સેમી અને 6 સેમી છે. જે વર્તુળનું ક્ષેત્રફળ આ બે વર્તુળનાં ક્ષેત્રફળના સરવાળા જેટલું હોય, તે વર્તુળની ત્રિજ્યા શોધો.
8 સેમી ત્રિજ્યાવાળા વર્તુળનું ક્ષેત્રફળ = π(8)2 સેમી2.
6 સેમી ત્રિજ્યાવાળા વર્તુળનું ક્ષેત્રફળ = π(6)2 સેમી2.
આ બે વર્તુળના ક્ષેત્રફળના સરવાળા જેટલું જે વર્તુળનું ક્ષેત્રફળ હોય તે વર્તુળની ત્રિજ્યા ધારો કે Rસેમી છે.
Rસેમી ત્રિજ્યાવાળા વર્તુળનું ક્ષેત્રફળ = π (R)2 સેમી2, તો આપેલ માહિતી મુજબ

3. આપેલ આકૃતિમાં તીરંદાજીનું લક્ષ્ય, કેન્દ્રથી બહારના ભાગ તરફ સોનેરી, લાલ, ભૂરું, કાળું અને સફેદ એમ પાંચ વિભાગમાં ગુણલક્ષણ દર્શાવે છે. ગુણની ગણતરી માટે સોનેરી રંગ દ્વારા દર્શાવાતા પ્રદેશનો વ્યાસ 21 સેમી છે અને દરેક વિભાગની પહોળાઈ 10.5 સેમી છે. ગણતરી કરવાના પાંચ પ્રદેશ પૈકી પ્રત્યેકનું ક્ષેત્રફળ શોધો.
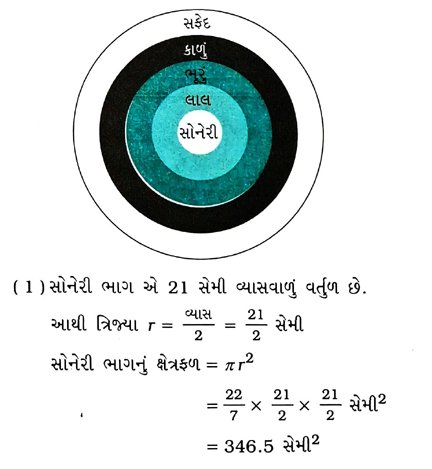

આમ, સોનેરી પ્રદેશનું ક્ષેત્રફળ 346.5 સેમી2, લાલ પ્રદેશનું ક્ષેત્રફળ 1039.5 સેમી2, ભૂરા પ્રદેશનું ક્ષેત્રફળ 1732.5 સેમી2, કાળા પ્રદેશનું ક્ષેત્રફળ 2425.5 સેમી2 અને સફેદ પ્રદેશનું ક્ષેત્રફળ 3118.5 સેમી2 છે.
4. એક ગાડીના દરેક પૈડાનો વ્યાસ 80 સેમી છે. જો ગાડી 66 કિમી / કલાકની ઝડપે મુસાફરી કરે, તો દરેક પૈડું 10 મિનિટમાં કેટલાં પરિભ્રમણ પૂર્ણ કરશે?

5. નીચેનામાંથી સાચા જવાબ પર નિશાન કરો અને તમારી પસંદગીની યથાર્થતા ચકાસો :
જો વર્તુળની પરિમિતિ અને ક્ષેત્રફળ સમાન સંખ્યા હોય, તો વર્તુળની ત્રિજ્યા ……… થાય.

મહત્ત્વનાં અન્ય ઉદાહરણો
1. બે વર્તુળના વ્યાસ અનુક્રમે 20 સેમી અને 48 સેમી છે. આ બે વર્તુળના ક્ષેત્રફળના સરવાળા જેટલું જે વર્તુળનું ક્ષેત્રફળ હોય તે વર્તુળનો વ્યાસ શોધો.
ધારો કે, જે વર્તુળનું ક્ષેત્રફળ d1 = 20 સેમી વ્યાસવાળા અને d2 = 48 સેમી વ્યાસવાળા વર્તુળના ક્ષેત્રફળના સરવાળા જેટલું હોય તેનો વ્યાસ D સેમી છે.

2. એક ટ્રૅક્ટરનાં આગળનાં પૈડાં તથા પાછળનાં પૈડાંના વ્યાસ અનુક્રમે 80 સેમી અને 2 મી છે. જેટલું અંતર કાપતાં આગળનાં પૈડાંનાં 1400 પરિભ્રમણ પૂર્ણ થાય તેટલું જ અંતર કાપતાં પાછળનાં પૈડાંનાં કેટલાં પરિભ્રમણ પૂર્ણ થાય તે શોધો.


3. બે વર્તુળોની ત્રિજ્યાઓનો તફાવત 7 સેમી છે અને તેમનાં ક્ષેત્રફળોનો તફાવત 1078 સેમી2 છે. બંને વર્તુળોની ત્રિજ્યા શોધો.
ધારો કે, મોટા વર્તુળની ત્રિજ્યા R સેમી અને નાના વર્તુળની ત્રિજ્યા r સેમી છે.

સમીકરણ (1) અને (2)નો ઉકેલ શોધતાં, R = 28 સેમી અને r = 21 સેમી છે.
આમ, મોટા અને નાના વર્તુળની ત્રિજ્યા અનુક્રમે 28 સેમી અને 21 સેમી છે.
પાઠ્યપુસ્તકનાં ઉદાહરણો


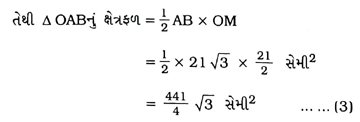

સ્વાધ્યાય – 12.2
1. જો 6 સેમી ત્રિજ્યાવાળા વર્તુળના વૃત્તાંશ દ્વારા કેન્દ્ર આગળ બનતો ખૂણો 60° હોય, તો વૃત્તાંશનું ક્ષેત્રફળ શોધો.
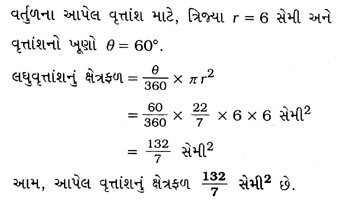
2. 22 સેમી પરિઘવાળા વર્તુળના ચતુર્થાંશનું ક્ષેત્રફળ શોધો.
ધારો કે, OAPB એ એક વર્તુળનો ચતુર્થાંશ છે અને તે વર્તુળનો પરિઘ 22 સેમી છે.

3. એક ઘડિયાળના મિનિટ-કાંટાની લંબાઈ 14 સેમી છે. મિનિટ- કાંટો 5 મિનિટમાં પરિભ્રમણ કરીને જે ક્ષેત્રફળ આવરે તે શોધો.
ઘડિયાળનો મિનિટ-કાંટો 60 મિનિટ, એટલે કે, 1 કલાકમાં એક પૂર્ણ પરિભ્રમણ કરે છે.


4. 10 સેમી ત્રિજ્યાવાળા વર્તુળની જીવા કેન્દ્ર આગળ કાટખૂણો આંતરે છે. તેને અનુરૂપ ( 1 ) લઘુવૃત્તખંડ ( 2 ) ગુરુવૃત્તાંશનું ક્ષેત્રફળ શોધો. (π = 3.14 લો.)
અહીં, વર્તુળની ત્રિજ્યા r = 10 સેમી અને લઘુવૃત્તાંશનો ખૂણો θ = 90°.

5. 21 સેમી ત્રિજ્યાવાળા વર્તુળનું એક ચાપ કેન્દ્ર આગળ 60નો ખૂણો આંતરે છે. તેને અનુરૂપ ( 1 ) ચાપની લંબાઈ ( 2 ) ચાપ વડે બનતા વૃત્તાંશનું ક્ષેત્રફળ (૩) અનુરૂપ જીવા વડે બનતા વૃત્તખંડનું ક્ષેત્રફળ શોધો.

6. 15 સેમી ત્રિજ્યાવાળા વર્તુળની જીવા કેન્દ્ર આગળ 60નો ખૂણો આંતરે છે. તેને અનુરૂપ લઘુવૃત્તખંડ અને ગુરુવૃત્તખંડનું ક્ષેત્રફળ શોધો. (π = 3.14 અને √3 = 1.73 લો.)
અહીં, વર્તુળની ત્રિજ્યા r = 15 સેમી અને જીવા AB કેન્દ્ર આગળ 60°નો ખૂણો આંતરે છે. આથી લઘુવૃત્તાંશ OAPBનો ખૂણો θ = 60°.

7. 12 સેમી ત્રિજ્યાવાળા વર્તુળની જીવા કેન્દ્ર આગળ 120°નો ખૂણો આંતરે છે. તેને અનુરૂપ વૃત્તખંડનું ક્ષેત્રફળ શોધો. (π = 3.14 અને √3 = 1.73 લો.)

8. 15 મી બાજુવાળા ચોરસ આકારના ઘાસના ખેતરના એક ખૂણે ઘોડાને 5 મી લાંબા દોરડાથી ખીલા સાથે બાંધેલો છે. (જુઓ આકૃતિ)

આથી ચરવાના ક્ષેત્રફળમાં થતો વધારો
= (78.5-19.625)મી² = 58.875 મી²
આમ, મૂળ પરિસ્થિતિ, એટલે કે દોરડાની લંબાઈ 5મી હોય, તો ઘોડો ખેતરમાં 19.625 મી² વિસ્તારમાં ચરી શકે અને જો દોરડાની લંબાઈ 10મી કરવામાં આવે, તો ઘોડો ચરી શકે તે વિસ્તારના ક્ષેત્રફળમાં 58.875 મી² નો વધારો થાય.
9. ચાંદીના તારથી 35 મિમી વ્યાસવાળું વર્તુળ આકારનું એક બક્કલ જેવું ઘરેણું બનાવ્યું છે. આપેલ આકૃતિમાં બતાવ્યા પ્રમાણે વર્તુળને 10 સમાન વૃત્તાંશમાં વિભાજિત કરે તેવા 5 વ્યાસ બનાવવામાં પણ તારનો ઉપયોગ કર્યો છે.
( 1 ) જરૂરી ચાંદીના તારની કુલ લંબાઈ શોધો.
( 2 ) ઘરેણાના દરેક વૃત્તાંશનું ક્ષેત્રફળ શોધો.

10. એક છત્રીમાં સમાન અંતરે 8 સળિયા આવેલા છે. (જુઓ આકૃતિ) છત્રીને 45 સેમી ત્રિજ્યાવાળું સમતલીય વર્તુળ ધારી, છત્રીના બે ક્રમિક સળિયા વચ્ચેના ભાગનું ક્ષેત્રફળ શોધો.

11. એક ગાડીને એકબીજા પર આચ્છાદિત ન થાય તેવાં બે વાઇપર છે. દરેક વાઇપરને 115°ના ખૂણા જેટલી સફાઈ કરતી 25 સેમી લંબાઈની બ્લેડ છે. પ્રત્યેક વખતે વાઇપરથી સાફ થતા વિસ્તારનું કુલ ક્ષેત્રફળ શોધો.
પ્રત્યેક વખતે વાઇપરથી સાફ થતા વિસ્તારનું ક્ષેત્રફળ બે લઘુવૃત્તાંશના કુલ ક્ષેત્રફળ જેટલું થાય.
અહીં, દરેક લઘુવૃત્તાંશ માટે ત્રિજ્યા r = 25 સેમી (વાઇપરની લંબાઈ) અને θ = 115°.

12. પાણીની નીચેના ખડકો વિશે જહાજને ચેતવણી આપવા માટે, એક દીવાદાંડી 16.5 કિમી અંતર સુધી 80° વૃત્તાંશના ખૂણે લાલ રંગનો પ્રકાશ પાથરે છે. સમુદ્રના જેટલા ક્ષેત્રફળ પર જહાજને ચેતવણી અપાતી હોય તે શેાધો. (π = 3.14 લો.)

13. આપેલ આકૃતિમાં બતાવ્યા પ્રમાણે એક વર્તુળાકાર મેજ પર છ ભાતવાળું એક આવરણ પાથરેલું છે. જો આવરણની ત્રિજ્યા 28 સેમી હોય, તો ₹ 0.35 પ્રતિ સેમીના દરે ડિઝાઇન બનાવવાનો ખર્ચ શોધો. (√3 = 1.7 લો.)


14. નીચેનામાં સાચા જવાબ આગળ નિશાની કરો :
R ત્રિજ્યાવાળા વર્તુળનો વૃત્તાંશ ખૂણો p॰ હોય, તો વૃત્તાંશનું ક્ષેત્રફળ ……. થાય.

મહત્ત્વનાં અન્ય ઉદાહરણો
1. એક વર્તુળની ત્રિજ્યા 21 સેમી છે. તે વર્તુળના એક લઘુવૃત્તાંશનો ખૂણો 120° છે, તો તે લઘુવૃત્તાંશ અને તેને અનુરૂપ ગુરુવૃત્તાંશનાં ક્ષેત્રફળોનો તફાવત શોધો.

2. 20 સેમી લાંબા એક તારને વાળીને વર્તુળના ચાપનો આકાર આપેલ છે. જો તે ચાપ અનુરૂપ વર્તુળના કેન્દ્ર આગળ 60નો ખૂણો બનાવે, તો તેને અનુરૂપ વર્તુળની ત્રિજ્યા શોધો.

3. 20 સેમી ત્રિજ્યાવાળા વર્તુળની એક જીવા કેન્દ્ર આગળ 90°નો ખૂણો આંતરે છે. તે જીવાને અનુરૂપ ગુરુવૃત્તખંડનું ક્ષેત્રફળ શોધો. ( π = 3.14 લો.)

પાઠ્યપુસ્તકનાં ઉદાહરણો
4. 56 મી બાજુવાળી ચોરસ લોન ABCDની બે સામસામેની બાજુઓ A પર ફૂલની બે વર્તુળાકાર ક્યારી આપેલ આકૃતિમાં બતાવી છે, તે રીતે બનાવી છે. જો ચોરસ લોનના વિકર્ણનું છેદબિંદુ O એ ફૂલની વર્તુળાકાર ક્યારીનું કેન્દ્ર હોય, તો લોન અને ફૂલની ક્યારીના ક્ષેત્રફળનો સરવાળો શોધો.



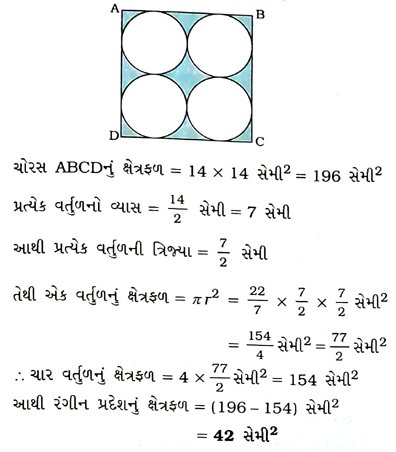
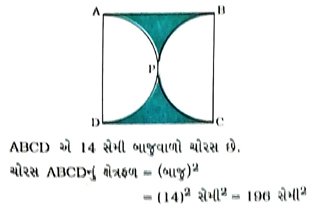
5. આપેલ આકૃતિમાં દર્શાવ્યા પ્રમાણેના 14 સેમી બાજુવાળા ચોરસ ABCDમાં આવેલા રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.
6. 10 સેમી બાજુવાળા ચોરસ ABCDની પ્રત્યેક બાજુ વ્યાસ હોય તેવાં અર્ધવર્તુળ આપેલ આકૃતિમાં દોરેલાં છે. આકૃતિમાં દર્શાવેલા રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો. (π = 3.14 લો.)

સ્વાધ્યાય – 12.3


2. જો ૩ કેપવાળાં બે સમકેન્દ્રી વર્તુળોની વિધા યુકમે 7 સેમી અને 14 એથી ૧૫ ∠AOC = 40″ હોય તો આપેલ આકૃતિમાં દર્શાવેલ રંગીન પ્રદેશનું શેહમ શોધો

3. 14 સેમી બાજુવાળા ચોરસ ABCDમાં જો અર્ધવર્તુળો APD અને BPC આવેલાં હોય, તો આપેલ આકૃતિમાં દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

4, 12 સેમી બાજુવાળા સમભુજ ત્રિકોણ OAB” શિરોબિંદુ O ને કેન્દ્ર તરીકે અને ત્રિજ્યા 6 સેમી લઈ, વર્તુળાકાર ચાપ દોર્યું છે, આપેલ આકૃતિમાં દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો,


5. આપેલ આકૃતિમાં દર્શાવ્યા પ્રમાણે 4 સેમી બાજુવાળા ચોરસના પ્રત્યેક ખૂણે 1 સેમી ત્રિજ્યાવાળા વર્તુળનો ચતુર્થાંશ ભાગ કપાયેલો છે તથા 2 સેમી વ્યાસવાળું એક વર્તુળ પણ કાપેલું છે. ચોરસના બાકીના ભાગનું ક્ષેત્રફળ શોધો.


6. આપેલ આકૃતિમાં દર્શાવ્યા પ્રમાણે ટેબલના એક 32 સેમી ત્રિજ્યાવાળા વર્તુળાકાર આવરણના વચ્ચેના ભાગમાં એક સમભુજ ત્રિકોણ ABC છોડી બાકીના ભાગમાં ભાત બનાવી છે. આ ભાતનું ક્ષેત્રફળ શોધો.

Δ ABC સમભુજ ત્રિકોણ હોવાથી વર્તુળની જીવાઓ AB, BC અને CA સમાન છે અને તેથી AB, BC અને CAને અનુરૂપ લઘુવૃત્તખંડ પણ સમાન અને સમક્ષેત્ર છે. આપણે BCને અનુરૂપ લઘુવૃત્તખંડનું ક્ષેત્રફળ શોધીએ.

7. આપેલ આકૃતિમાં 14 સેમી બાજુવાળો ચોરસ ABCD છે. પ્રત્યેક વર્તુળ બાકીનાં ત્રણ વર્તુળોમાંથી બે વર્તુળને બહારથી સ્પર્શે તેમ A, B, C અને D કેન્દ્રવાળાં ચાર વર્તુળ દોર્યાં છે. દર્શાવેલા રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

ચોરસ ABCD માટે, બાજુ a = 14 સેમી
ચોરસ ABCDનું ક્ષેત્રફળ = a2
= (14)2 સેમી2
= 196 સેમી2
A, B, C અને D કેન્દ્રવાળાં ચાર વર્તુળો પૈકી પ્રત્યેક વર્તુળ બાકીનાં ત્રણ વર્તુળોમાંથી બે વર્તુળોને બહારથી સ્પર્શે છે. આથી પ્રત્યેક વર્તુળની ત્રિજ્યા ચોરસ ABCDની બાજુ કરતાં અડધી થાય.

8. આપેલ આકૃતિમાં દોડમાર્ગનું નિરૂપણ કરેલું છે. તેના ડાબા અને જમણા છેડા અર્ધવર્તુળાકાર છે. અંદરના બે સમાંતર રેખાખંડ વચ્ચેનું અંતર 60 મી છે અને તે પ્રત્યેકની લંબાઈ 106 મી છે. જો માર્ગ 10 મી પહોળો હોય, તો ( 1 ) માર્ગની અંદરની ધારનું ચારેય તરફનું અંતર શોધો. ( 2 ) માર્ગનું ક્ષેત્રફળ શોધો.
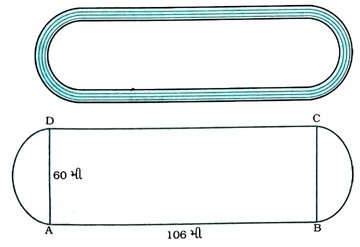
દોડમાર્ગનો અંદરની તરફનો ભાગ બે રેખાખંડ AB અને CD તથા બે અર્ધવર્તુળ AD અને BC દ્વારા ઘેરાયેલ બંધ આકૃતિ રચે છે. દરેક રેખાખંડની લંબાઈ 106 મી છે તથા દરેક અર્ધવર્તુળનો વ્યાસ અંદરના બે સમાંતર રેખાખંડ AB અને CD વચ્ચેના અંતર જેટલો, એટલે કે, 60 મી છે. 60 મી વ્યાસવાળા દરેક


આથી રંગીન પ્રદેશનું કુલ ક્ષેત્રફળ
= (28 + 38.5) સેમી2
= 66.5 સેમી2
આમ, રંગીન પ્રદેશનું ક્ષેત્રફળ 66.5 સેમી2 છે.
10. એક સમભુજ ત્રિકોણ ABCનું ક્ષેત્રફળ 17320.5 સેમી છે. ત્રિકોણની બાજુની લંબાઈથી અડધી ત્રિજ્યાવાળા અને પ્રત્યેક શિરોબિંદુ કેન્દ્ર હોય તેવાં વર્તુળ દોર્યાં છે. (જુઓ આકૃતિ) દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.

11. એક ચોરસ હાથરૂમાલ પર 7 સેમી ત્રિજ્યાવાળી નવ વર્તુળાકાર ભાત બનાવી છે. (જુઓ આકૃતિ) હાથરૂમાલના બાકીના ભાગનું ક્ષેત્રફળ શોધો.

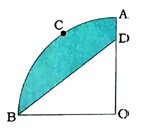
12. આપેલ આકૃતિમાં દર્શાવેલ ચતુર્થાંશ OACBનું કેન્દ્ર O છે અને ત્રિજ્યા 3.5 સેમી છે. જો OD = 2 સેમી હોય, તો, ( 1 ) ચતુર્થાંશ OACDનું ક્ષેત્રફળ શોધો. ( 2 ) દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો.


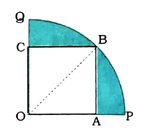
13. આપેલ આકૃતિમાં, એક વર્તુળના ચતુર્થાંશ OPBQની અંતર્ગત ચોરસ OABC છે. જો OA = 20 સેમી હોય, તો દર્શાવેલ રંગીન પ્રદેશનું ક્ષેત્રફળ શોધો. (π = 3.14 લો.)

મહત્ત્વનાં અન્ય ઉદાહરણો
1. આપેલ આકૃતિમાં છાયાંકિત પ્રદેશનું ક્ષેત્રફળ શોધો. (π = 3.14 લો.)

2. તીરંદાજીનું લક્ષ્ય આકૃતિમાં બતાવ્યા મુજબનાં ત્રણ સમકેન્દ્રી વર્તુળો દ્વારા બનાવેલ છે. જો તે ત્રણ વર્તુળોના વ્યાસ 1 : 2 : 3ના ગુણોત્તરમાં હોય, તો લક્ષ્યના ત્રણ પ્રદેશોનાં ક્ષેત્રફળોનો ગુણોત્તર શોધો.

આપેલ વર્તુળોના વ્યાસનો ગુણોત્તર 1 : 2 : 3 છે.
આથી આપેલ વર્તુળોની ત્રિજ્યાઓનો ગુણોત્તર પણ 1 : 2 : 3 થાય.
ધારો કે, આ વર્તુળોની ત્રિજ્યા અંદરના વર્તુળથી બહારના વર્તુળ માટે અનુક્રમે r, 2r અને 3r એકમ છે.
અંદરના પ્રદેશથી બહારના પ્રદેશનાં ક્ષેત્રફળોને અનુક્રમે A1, A2 અને A3 દ્વારા દર્શાવતાં,

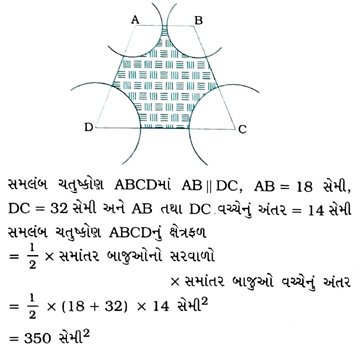
3. આપેલ આકૃતિમાં ABCD એક સમલંબ ચતુષ્કોણ છે. જેમાં AB || DC, AB = 18 સેમી, DC = 32 સેમી અને AB તથા DC વચ્ચેનું અંતર = 14 સેમી છે. શિરોબિંદુઓ A, B, C અને Dને કેન્દ્ર લઈને 7 સેમી ત્રિજ્યાવાળા ચાપ દોરેલ છે. આકૃતિમાં દર્શાવેલ છાયાંકિત પ્રદેશનું ક્ષેત્રફળ શોધો.


હેતુલક્ષી પ્રશ્નોત્તર
1, પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
( 1 ) એક વર્તુળ માટે પરિઘ અને ત્રિજ્યાનો તફાવત 37 સેમી છે. આથી વર્તુળનો પરિઘ ……. સેમી હોય,
( 2 ) r સેમી ત્રિજ્યાવાળા અર્ધવર્તુળને અંતર્ગત હોય તેવા ત્રિકોણનું ક્ષેત્રફળ વધુમાં વધુ ……. સેમી2 હોય.
( 3 ) 6.5 સેમી ત્રિજ્યાવાળા એક વર્તુળના વૃત્તાંશની પરિમિતિ 29 સેમી છે, તો તે વૃત્તાંશનું ક્ષેત્રફળ ……. સેમા2 થાય.
( 4 ) જો વર્તુળની ત્રિજ્યાના માપમાં 10% ઘટાડો કરવામાં આવે, તો તેના ક્ષેત્રફળમાં …….. %નો ઘટાડો થાય.
( 5 ) 28 સેમી ત્રિજ્યાવાળા વર્તુળના એક ચતુર્થાંશનું ક્ષેત્રફળ …… સેમી2 થાય.
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
( 1 ) આપેલ આકૃતિમાં, વૃત્તખંડ PAOનું ક્ષેત્રફળ = …….. સેમી2.

( 2 ) એક વર્તુળના વૃત્તાંશનું ક્ષેત્રફળ 20 π સેમી2 છે તથા તેને સંગત ચાપની લંબાઈ 51 સેમી છે, તો વર્તુળની ત્રિજ્યા …… સેમી હોય.
A. 12
B. 16
C. 8
D. 10
( 3 ) જો એક વર્તુળ અને ચોરસની પરિમિતિઓ સમાન હોય, તો તેમના ક્ષેત્રફળોનો ગુણોત્તર …….. થાય.
A. 22 : 7
B. 14 : 11
C. 7 : 22
D. 11 : 14
( 4 ) શહેરના એક વિસ્તારમાં 16 મી વ્યાસ અને 12 મી વ્યાસના વર્તુળાકાર બે બગીચા છે. તે બગીચાના કુલ ક્ષેત્રફળ જેટલું ક્ષેત્રફળ ધરાવતો નવો વર્તુળાકાર બગીચો બનાવવો હોય, તો તે બગીચાની ત્રિજ્યા …….. મી રાખવી જોઈએ.
A. 10
B. 15
C. 20
D. 24
( 5 ) 6 સેમીની બાજુ ધરાવતા ચોરસને અંતર્ગત વર્તુળનું ક્ષેત્રફળ …….. સેમી2 થાય.
A. 36л
B. 18л
C. 12л
D. 9л
( 6 ) એક વર્તુળનું ક્ષેત્રફળ 24 સેમી ત્રિજ્યા અને 7 સેમી ત્રિજ્યા ધરાવત બે વર્તુળોનિ ક્ષેત્રફળોના સરવાળા જેટલું છે, તો તે વર્તુળનો વ્યાસ ……. સેમી હોય.
A, 31
B. 25
C. 62
D. 50
( 7 ) 8 સેમી ત્રિજ્યાવાળા વર્તુળને અંતર્ગત હોય તેવા ચોરસન્ ક્ષેત્રફળ ……… સેમી2 થાય.
A. 256
B. 128
C. 64√2
D, 64
( 8 ) 35 સેમી વ્યાસ ધરાવતું એક પૈડું એક પરિભ્રમણમાં ………. મી અંતર કાપે,
A. 2.2
B. 1.1
C. 9,625
D. 96,25
( 9 ) r1 અને r2 ત્રિજ્યા ધરાવતાં વર્તુળોના પરિઘના સરવાળા જેટલો પરિઘ ધરાવતા એક વર્તુળની ત્રિજ્યા r છે, તો ….. વિધાન સાચું છે.
A. r = r1 + r2
B. r < r1 + r2
C. r > r1 + r2
D. આપેલ પૈકી એક પણ નહીં
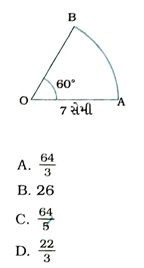
(10) આકૃતિમાં આપેલ વૃત્તાંશ OABની પિરિમિત …….. સેમી થાય.
3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ લખો :
( 1 ) જો એક ચોરસ અને વર્તુળનાં ક્ષેત્રફળો સમાન હોય, તો તેમની પરિમિતિઓનો ગુણોત્તર શોધો.
( 2 ) જો r ત્રિજ્યા ધરાવતા વર્તુળનું ક્ષેત્રફળ અને r1 અને r2 ત્રિજ્યા ધરાવતાં બે વર્તુળોનાં ક્ષેત્રફળોનો સરવાળો સમાન હોય, તો r, r1 અને r2 વચ્ચેનો સંબંધ શોધો.
( 3 ) જો કોઈ વર્તુળની પરિમિતિ તથા તેનું ક્ષેત્રફળ આંકડાકીય રીતે સમાન હોય, તો તે વર્તુળનો વ્યાસ શોધો.
( 4 ) એક વર્તુળાકાર બગીચાની ફરતે બહારની બાજુએ સમાન પહોળાઈનો કંકણાકાર રસ્તો છે. જો કંકણાકાર રસ્તાના બહારના પરિઘ અને અંદરના પરિઘનો તફાવત 132 મી હોય, તો રસ્તાની પહોળાઈ શોધો.
( 5 ) એક વર્તુળનું ક્ષેત્રફળ 220 સેમી2 છે. આ વર્તુળને અંતર્ગત હોય તેવા ચોરસનું ક્ષેત્રફળ શોધો.
( 6 ) 8 સેમી ત્રિજ્યાવાળા વર્તુળમાં અંતર્ગત ચોરસનું ક્ષેત્રફળ શોધો.
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) a સેમી ત્રિજ્યાવાળા વર્તુળને પરિગત હોય તેવા ચોરસની પરિમિત 8 a સેમી થાય.
( 2 ) d સેમી વ્યાસ ધરાવતું પૈડું એક પરિભ્રમણમાં 2 π d સેમી અંતર કાપે.
( 3 ) વર્તુળના કોઈ પણ વૃત્તખંડનું ક્ષેત્રફળ તેને અનુરૂપ વૃત્તાંશના ક્ષેત્રફળ કરતાં ઓછું હોય.
( 4 ) કોઈ પણ વર્તુળના ક્ષેત્રફળનું આંકડાકીય મૂલ્ય તે વર્તુળના પરિઘના આંકડાકીય મૂલ્ય કરતાં હંમેશાં અધિક જ હોય.
( 5 ) જો બે જુદાં જુદાં વર્તુળોના બે વૃત્તાંશના ક્ષેત્રફળ સમાન હોય, તો તે વૃતાંશોને અનુરૂપ ચાપની લંબાઈ સમાન હોય.
( 6 ) વર્તુળના પરિઘ અને વ્યાસનો ગુણોત્તર અચળ છે.

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here