Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 13 Surface Areas and Volumes (પૃષ્ઠફળ અને ઘનફળ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 13 Surface Areas and Volumes (પૃષ્ઠફળ અને ઘનફળ)
સ્વાધ્યાય – 13.1
1. બે ઘન પૈકી પ્રત્યેકનું ઘનફળ 64 સેમી હોય તેવા બે ઘનને જોડવાથી બનતા લંબઘનનું પૃષ્ઠફળ શોધો.
ધારો કે, આપેલ બે ઘન પૈકી પ્રત્યેકની ધારનું માપ a સેમી છે.
ઘનનું ઘનફળ = a3
∴ 64 = a3
∴ a = 4 સેમી

આપેલ બે ઘનને જોડતાં બનતા લંબઘન માટે,
લંબાઈ l = (4 + 4) સેમી = 8 સેમી, પહોળાઈ b = 4 સેમી અને ઊંચાઈ h = 4 સેમી
લંબઘનનું પૃષ્ઠફળ = 2 (lb + bh + hl)
= 2 (8 × 4 + 4 × 4 + 4 × 8) સેમી2
= 2 (80) સેમી2
= 160 સેમી2
2. એક અર્ધગોલક ઉપર એક પોલો નળાકાર બેસાડેલો હોય તેવું એક પાત્ર છે. અર્ધગોલકનો વ્યાસ 14 સેમી છે અને પાત્રની કુલ ઊંચાઈ 13 સેમી છે. પાત્રની અંદરની સપાટીનું પૃષ્ઠફળ શોધો.

3. અર્ધગોલકની ઉપર શંકુ લગાવેલો હોય તેવું એક રમકડું છે. તે બંનેની ત્રિજ્યા 3.5 સેમી છે. રમકડાની કુલ ઊંચાઈ 15.5 સેમી હોય, તો રમકડાનું કુલ પૃષ્ઠફળ શોધો.


4. 7 સેમી બાજુના માપવાળા સમઘનની ઉપર અર્ધગોલક મૂકેલો છે, તો અર્ધગોલકનો મહત્તમ વ્યાસ શું હોઈ શકે? આ રીતે બનેલા પદાર્થનું કુલ પૃષ્ઠફળ શોધો.

5. એક સમઘન લાકડાના ટુકડાના એક પૃષ્ઠમાંથી એક અર્ધગોલક કાપવામાં આવે છે. અર્ધગોલકનો વ્યાસ l એ સમઘનની બાજુના માપ બરાબર છે, તો બાકી પદાર્થનું કુલ પૃષ્ઠફળ શોધો.

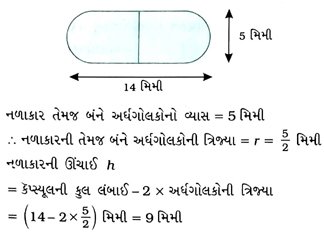
6. દવાની એક કૅપ્સ્યૂલનો આકાર નળાકારની બંને બાજુએ અર્ધગોલક લગાડેલા હોય તે રીતનો છે. (જુઓ આકૃતિ) કૅપ્સ્યૂલની લંબાઈ 14 મિમી છે અને તેનો વ્યાસ 5 મિમી છે, તો કૅપ્સ્યૂલનું પૃષ્ઠફળ શોધો.

7. એક તંબુનો આકાર નળાકાર ઉપર શંકુ મૂકવામાં આવેલ હોય તેવો છે. જો નળાકાર ભાગની ઊંચાઈ અને વ્યાસ અનુક્રમે 2.1 મીટર અને 4 મીટર હોય તથા ઉપરના ભાગની તિર્યક ઊંચાઈ 2.8 મીટર હોય, તો આ તંબુ બનાવવા વપરાતા કૅન્વાસનું ક્ષેત્રફળ શોધો અને જો કૅન્વાસનો ભાવ ₹ 500 પ્રતિ મીટર2 હોય, તો તેમાં વપરાતા કૅન્વાસની કિંમત પણ શોધો. (તંબુના તળિયાને કૅન્વાસથી ઢાંકવામાં આવતો નથી તે ધ્યાનમાં લેવું.)

આમ, તંબુ બનાવવા વપરાતા કૅન્વાસનું ક્ષેત્રફળ 44 મી2 થાય અને કૅન્વાસની કિંમત ₹ 22,000 થાય.
8. નળાકાર પદાર્થની ઊંચાઈ 2.4 સેમી અને વ્યાસ 1.4 સેમી છે. તેમાંથી તેટલી જ ઊંચાઈ અને વ્યાસવાળો શંકુ કાપી લેવામાં આવે, તો વધેલા પદાર્થનું કુલ પૃષ્ઠફળ નજીકના સેમીમાં શોધો.


9. આપેલ આકૃતિમાં દર્શાવ્યા પ્રમાણે લાકડાના નળાકારમાંથી બંને બાજુએથી અર્ધગોલક કાઢી એક લાકડાનો શો-પીસ બનાવ્યો છે. જો નળાકારની ઊંચાઈ 10 સેમી હોય અને પાયાની ત્રિજ્યા 3.5 સેમી હોય, તો શો-પીસનું કુલ પૃષ્ઠફળ શોધો.

મહત્ત્વનાં અન્ય ઉદાહરણો
1. અંદરથી પોલા એવા એક અર્ધગોલક આકારના પાત્રનો અંદરનો અને બહારનો વ્યાસ અનુક્રમે 12 સેમી અને 16 સેમી છે. જો 1 સેમી2 સપાટીને રંગ કરવાનો ખર્ચ ૬ 5.00 હોય, તો પાત્રને પૂર્ણ રીતે રંગવાનો ખર્ચ શોધો. (π = 3.14 લો.)



2. એક બંધ નળાકાર પાત્રની બહારની કુલ સપાટીને રંગવાનો ખર્ચ 60 પૈસા પ્રતિ સેમી લેખે ₹ 237.60 થાય છે. જો નળાકારની ઊંચાઈ તેના પાયાની ત્રિજ્યા કરતાં 6 ગણી હોય, તો નળાકાર પાત્રની ઊંચાઈ અને ત્રિજ્યા શોધો.

પાઠ્યપુસ્તકનાં ઉદાહરણો
5. શાંતા શેડમાં એક ઉદ્યોગ ચલાવે છે. આ શેડનો આકાર લંબઘન ઉપર અર્ધનળાકારથી બંધ છે. (જુઓ આકૃતિ) તે શેડના પાયાનું માપ 7 મી × 15 મી, અને લંબઘનાકારની ઊંચાઈ 8મી હોય, તો આ શેડમાં સમાતી હવાનું ઘનફળ શોધો. ઉપરાંત, શેડમાં મશીનરીના ભાગનું કુલ ઘનફળ 300 મી3 અને 20 કારીગરો પૈકી પ્રત્યેક કારીગરે રોકેલી જગ્યાનું ઘનફળ 0.08 મી3 છે, તો
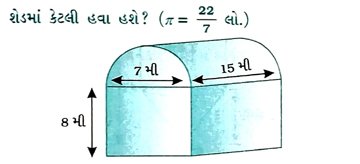
શેડની હવાનું ઘનફળ (જ્યારે શેડમાં કારીગરો અને મશીનરી ન હોય) એ લંબઘન અને અર્ધનળાકારની અંદર રહેલી હવાના ઘનફળના સરવાળા જેટલું છે.
હવે, લંબઘનની લંબાઈ, પહોળાઈ અને ઊંચાઈ અનુક્રમે 15 મી, 7મી અને 8મી છે. પણ, અર્ધનળાકારનો વ્યાસ 7મી અને તેની ઊંચાઈ 15 મી છે.

6. એક જ્યૂસ વેચવાવાળો તેના ગ્રાહકોને આપેલ આકૃતિમાં દર્શાવ્યા પ્રમાણેના પ્યાલામાં જ્યૂસ આપતો હતો. નળાકાર પ્યાલાનો અંદરનો વ્યાસ 5 સેમી છે, પરંતુ પ્યાલાના પાયામાં અર્ધગોલક ભાગ ઉપસી આવેલો હતો. જેથી પ્યાલાની ક્ષમતા ઓછી થતી હતી. જો પ્યાલાની ઊંચાઈ 10 સેમી હોય, તો તેની આભાસી ક્ષમતા તથા તેની વાસ્તવિક ક્ષમતા શોધો. (π = 3.14 લો.)

પ્યાલાની અંદરનો વ્યાસ = 5 સેમી અને ઊંચાઈ = 10 સેમી છે, જેથી પ્યાલાની આભાસી ક્ષમતા

7. એક નક્કર રમકડું એ અર્ધગોલકની ઉપર શંકુ લગાવ્યો હોય તેવા સ્વરૂપે છે. શંકુની ઊંચાઈ 2 સેમી અને પાયાનો વ્યાસ 4 સેમી છે, તો ૨મકડાનું ઘનફળ શોધો. જો એક લંબવૃત્તીય નળાકાર રમકડાને પરિગત હોય, તો નળાકારના અને રમકડાના ઘનફળનો તફાવત શોધો. (π = 3.14 લો.) (જુઓ આકૃતિ)


સ્વાધ્યાય – 13.2
1. એક ઘન પદાર્થ એ 1 સેમી ત્રિજ્યા ધરાવતા અર્ધગોલક ઉપર તેટલી જ ત્રિજ્યાવાળો શંકુ ગોઠવીને બનાવાયો છે. શંકુની ઊંચાઈ એ તેની ત્રિજ્યા જેટલી છે, તો આ ઘન પદાર્થનું ઘનફળ ના ગુણિતમાં શોધો.

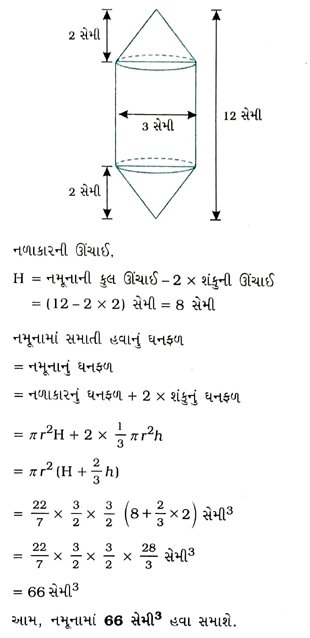
2. એન્જિનિયરિંગના વિદ્યાર્થી રશેલને નળાકારના બંને છેડે પાતળી ઍલ્યુમિનિયમની શીટમાંથી બનેલો શંકુ બેસાડી એક નમૂનો તૈયાર કરવાનું કહેવામાં આવ્યું. નમૂનાનો વ્યાસ 3 સેમી અને લંબાઈ 12 સેમી છે. જો શંકુની ઊંચાઈ 2 સેમી હોય, તો ૨શેલે બનાવેલ નમૂનામાં કેટલી હવા સમાશે તે શોધો. (ધારી લો કે, નમૂનાના બહારના અને અંદરના માપો લગભગ સમાન છે.)

3. ગુલાબજાંબુમાં તેના કદના 30 % જેટલી ખાંડની ચાસણી છે. દરેક ગુલાબજાંબુનો આકાર નળાકારના બંને છેડે અર્ધગોલક લગાવ્યા હોય તેવો છે. તેની કુલ લંબાઈ 5 સેમી અને વ્યાસ 2.8 સેમી છે, તો આવા 45 ગુલાબજાંબુમાં આશરે કેટલી ખાંડની ચાસણી હશે તે શોધો. (જુઓ આકૃતિ 1)

4. એક લાકડાનું લંબઘન પેન-સ્ટૅન્ડ ચાર શંકુ આકારના છિદ્રવાળું બનાવેલું છે. લંબઘનનાં માપ 15 સેમી × 10 સેમી × 3.5 સેમી છે. છિદ્રવાળા દરેક ભાગની ત્રિજ્યા 0.5 સેમી અને ઊંડાઈ 1.4 સેમી છે, તો લાકડાના આ સ્ટેન્ડનું ઘનફળ શોધો. (જુઓ આકૃતિ)

5. એક વાસણનું સ્વરૂપ ઊંધા શંકુ જેવું છે. તેની ઊંચાઈ 8 સેમી અને ઉપરના ભાગની ત્રિજ્યા 5 સેમી છે. તે ઉપરની ધાર સુધી પાણીથી ભરેલું છે. જ્યારે વાસણમાં 0.5 સેમી ત્રિજ્યાવાળી ધાતુની ગોળીઓ નાખવામાં આવે છે, ત્યારે એક-ચતુર્થાંશ જેટલું પાણી બહાર નીકળે છે, તો વાસણમાં નાખેલી ધાતુની ગોળીઓની સંખ્યા શોધો.


6. એક લોખંડના નળાકાર સ્વરૂપના નક્કર થાંભલાની ઊંચાઈ 220 સેમી છે અને પાયાનો વ્યાસ 24 સેમી છે. તેની ઉપર 60 સેમી ઊંચાઈ અને 8 સેમી ત્રિજ્યાવાળા બીજા નળાકારને મૂકવામાં આવે છે, તો થાંભલાનું દળ શોધો. 1 સેમી॰ લોખંડનું દળ આશરે 8 ગ્રામ છે. (π = 3.14 લો.)

7. 60 સૈમી ત્રિજ્યાવાળા અર્થોલક પર સ્થિત લંબવૃત્તીય શંકુની ઊંચાઈ 120 ગેમી અને ત્રિજ્યા 60 સેમી છે. તેને પાણીથી સંપૂર્ણ ભરેલા એક લંબવૃત્તીય નળાકારમાં તેના તળિયાને સ્પર્શ તે તે ઊો મૂક્યો છે, જો નળાકારની ત્રિજ્યા 60 સેમી અને ઊંચાઈ 180 શેમી હોય, તો નળાકારમાં બાકી રહેલા પાણીનું ધનળ શોધો.
સંયોજિત ઘન પદાર્થ માટે, શકુની ત્રિજ્યા = અર્ધગોલકની ત્રિજ્યા = r = 60 સેમી અને શકુની ઊંચાઈ = h = 120 સેમી સોજિત ઘન પદાર્થનું ઘનફળ

8. એક ગોળાકાર કાચના વાસણની ઉપરનો ભાગ નળાકાર છે. તે નળાકારની ઊંચાઈ 8 સેમી છે અને વ્યાસ 2 સેમી છે. ગોળાકાર ભાગનો વ્યાસ 8.5 સેમી છે. એક બાળક માહિતી પ્રાપ્ત કરે છે કે તેમાં ભરેલા પાણીનું ઘનફળ 345 સેમી છે. બાળકનો જવાબ સાચો છે કે નહિ તે ચકાસો. ઉપરનાં માપો તેના અંદરના ભાગના છે. π = 3.14 લો.


મહત્ત્વનાં અન્ય ઉદાહરણો
1. એક નક્કર નળાકારની ત્રિજ્યા અને ઊંચાઈનો સરવાળો 37 સેમી છે. જો તે નળાકારની કુલ સપાટીનું ક્ષેત્રફળ 1628 સેમી હોય, તો તેનું ઘનફળ શોધો.
ધારો કે, નળાકારની ત્રિજ્યા અને ઊંચાઈ અનુક્રમે r સેમી અને h સેમી છે.

2. એક તંબુ નીચે નળાકાર અને ઉપર શંકુ આકારનો છે. નળાકાર ભાગનો વ્યાસ 4.2 મી તથા ઊંચાઈ 8મી છે. નળાકાર પર બંધબેસતા શંકુની ઊંચાઈ 6મી છે. તંબુમાં રહેલી હવાનું ઘનફળ શોધો.


3. એક પાત્ર અર્ધગોલક પર બંધબેસતો પોલો નળાકાર ગોઠવીને બનાવેલ છે. અર્ધગોલકનો વ્યાસ 14 સેમી અને પાત્રની કુલ ઊંચાઈ 13 સેમી છે. પાત્રની ક્ષમતા શોધો.

પાઠ્યપુસ્તકનાં ઉદાહ૨ણો
8. નમૂના બનાવવાની માટીમાંથી 24 સેમી ઊંચાઈ અને 6 સેમી પાયાની ત્રિજ્યાવાળો એક શંકુ બનાવેલો છે. એક બાળકે તેને ગોળાકાર સ્વરૂપમાં પરિવર્તિત કરી નાખ્યો છે, તો ગોળાની ત્રિજ્યા શોધો.
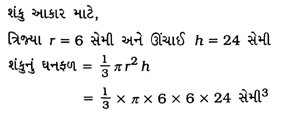

9. સેલ્વીના ઘરની છત ઉપર નળાકાર આકારની એક ટાંકી છે. આમાં ભોંયતળિયાની લંબઘન ટાંકીમાંથી પંપ દ્વારા પાણી ભરવામાં આવે છે. આ ભૂગર્ભની ટાંકી ઘનાકાર છે. ટાંકીનાં માપ 1.57 મીટર × 1.44 મીટર × 95 સેમી છે. છત ઉપરની ટાંકીની ત્રિજ્યા 60 સેમી છે અને ઊંચાઈ 95 સેમી છે. જો ભોંયતળિયાની ટાંકી પાણીથી પૂરેપૂરી ભરેલી હોય, તો તેમાંથી છત ઉપરની ટાંકીને પૂરેપૂરી ભરી લીધા પછી ભોંયતળિયાની ટાંકીમાં પાણીની ઊંચાઈ કેટલી બાકી રહેશે? છતની ટાંકીની ક્ષમતાની સાથે ભોંયતળિયાની ટાંકીની ક્ષમતાની સરખામણી કરો. (π = 3.14 લો.)

10. 1 સેમી વ્યાસ અને 8 સેમી લંબાઈવાળો એક તાંબાનો સળિયો છે. તેમાંથી 18 મીટર લંબાઈનો એકસરખી જાડાઈવાળો તાર બનાવવો છે, તો તારની જાડાઈ શોધો.


સ્વાધ્યાય – 13.3
1. 4.2 સેમી ત્રિજ્યાવાળા ધાતુના ગોલકને ઓગાળીને 6 સેમી ત્રિજ્યાવાળા નળાકાર સ્વરૂપમાં રૂપાંતરિત કરવામાં આવે છે. નળાકારની ઊંચાઈ શોધો.

2. 6 સેમી, 8 સેમી અને 10 સેમી ત્રિજ્યાવાળા ધાતુના ગોળાઓને ઓગાળીને એક મોટો નક્કર ગોળો બનાવવામાં આવે છે, તો આ રીતે બનતા ગોળાની ત્રિજ્યા શોધો.
ધારો કે, ઓગાળવામાં આવેલ ત્રણ ગોળાઓની ત્રિજ્યાઓ r1, r2 અને r3 છે તથા પરિણામી ગોળાની ત્રિજ્યા R છે, તો r1 = 6 સેમી; r2 = 8 સેમી અને r3 = 10 સેમી

3. એક કૂવો 7 મીટર વ્યાસવાળા વર્તુળ પર 20 મીટર સુધી ખોદવામાં આવે છે અને તે ખોદવાથી નીકળેલી માટીને એકસરખી રીતે પાથરી 22 મીટર × 14 મીટરની એક વ્યાસપીઠ બનાવવામાં આવે છે, તો વ્યાસપીઠની ઊંચાઈ શોધો.
નળાકાર કૂવા માટે ત્રિજ્યા r = 7/2 મી અને ઊંચાઈ (ઊંડાઈ) h = 20 મી.

4. 3 મીટર વ્યાસવાળા એક વર્તુળ પર એક કૂવો 14 મીટર સુધી ખોદવામાં આવે છે. તેમાંથી નીકળેલી માટીને કૂવાની આસપાસ 4 મીટર પહોળા વર્તુળાકાર વલયમાં સમાન રીતે પાથરીને ઓટલો બનાવ્યો છે, તો ઓટલાની ઊંચાઈ શોધો.

5. 12 સેમી વ્યાસ અને 15 સેમી ઊંચાઈવાળા એક પાત્રનો આકાર લંબવૃત્તીય નળાકાર છે. તે આઇસક્રીમથી સંપૂર્ણ ભરેલો છે. તેમાંથી 12 સેમી ઊંચાઈ અને 6 સેમી વ્યાસવાળા શંકુ આકારના કોન પર અર્ધગોળાકાર સ્વરૂપમાં આઇસક્રીમ ભરવામાં આવે છે, તો આ આઇસક્રીમ દ્વારા કેટલા કોન ભરી શકાય તે શોધો.

6. 5.5 સેમી × 10 સેમી × 3.5 સેમીના માપનો લંબઘન બનાવવા 1.75 સેમી વ્યાસ અને 2 મિમી જાડાઈવાળા ચાંદીના કેટલા સિક્કા ઓગાળવા પડે?


આમ, જરૂરી માપનો લંબઘન બનાવવા માટે 400 સિક્કા ઓગાળવા પડે.
7. 32 સેમી ઊંચાઈ અને પાયાની ત્રિજ્યા 18 સેમી હોય તેવી એક નળાકાર ડોલ રેતીથી ભરેલી છે. આ ડોલને જમીન પર ખાલી કરી શંકુ આકારનો ઢગલો બનાવ્યો છે. જો શંકુ આકારના ઢગલાની ઊંચાઈ 24 સેમી હોય, તો ઢગલાની ત્રિજ્યા અને તિર્યક ઊંચાઈ શોધો.

8. 6 મીટર પહોળી અને 1.5 મીટર ઊંડી એક પાણીની નહેરમાં પાણી 10 કિમી / કલાકની ઝડપે વહે છે. 30 મિનિટમાં આ નહેરમાંથી કેટલા ક્ષેત્રફળની સિંચાઈ કરી શકાશે? સિંચાઈ માટે 8 સેમી પાણીની ઊંચાઈ આવશ્યક છે.
નહેરમાં વહેતા પાણી માટે, તેમાંથી 30 મિનિટ દરમિયાન વહેતા પાણીનું ઘનફળ લંબઘનના ઘનફળ દ્વારા મળે, જે લંબઘન માટે પહોળાઈ b = 6 મી (નહેરની પહોળાઈ), ઊંચાઈ h = 1.5 મી (નહેરની ઊંડાઈ) અને લંબાઈ l = 30 મિનિટના સમયગાળામાં પાણીના પ્રવાહે કાપેલ અંતર = ઝડપ × સમય

9. એક ખેડૂત પોતાના ખેતરમાં 10 મીટર વ્યાસવાળી અને 2 મીટર ઊંડી એક નળાકાર ટાંકીને અંદરથી 20 સેમી વ્યાસવાળી એક પાઇપ દ્વારા એક નહેર સાથે જોડે છે. જો પાઇપમાં પાણીનો પ્રવાહ 3 કિમી / કલાકની ઝડપે વહેતો હોય, તો કેટલા સમયમાં ટાંકી પાણીથી પૂર્ણ રીતે ભરાઈ જશે?

મહત્ત્વનાં અન્ય ઉદાહરણો
1. ધાતુના એક લંબઘનનું માપ 66 સેમી × 42 સેમી × 21 સેમી છે. તે લંબઘનને ઓગાળીને 4.2 સેમી વ્યાસવાળી ગોળીઓ બનાવવામાં આવે, તો કેટલી ગોળીઓ બને?
ધાતુના લંબઘન માટે, લંબાઈ l = 66 સેમી, પહોળાઈ b = 42 સેમી અને ઊંચાઈ h = 21 સેમી.
ધાતુના લંબઘનનું ઘનફળ = lbh = 66 × 42 × 21 સેમી3 ગોલક આકારની દરેક ગોળી માટે,


2. 10.5 સેમી ત્રિજ્યાવાળા ધાતુના એક ગોલકને ઓગાળીને તેમાંથી 3.5 સેમી ત્રિજ્યા અને 3 સેમી ઊંચાઈવાળા શંકુ બનાવવામાં આવે છે. આ રીતે બનતા શંકુઓની સંખ્યા શોધો.
ધાતુના ગોલક માટે, ત્રિજ્યા R = 10.5 સેમી
દરેક શંકુ માટે,
ત્રિજ્યા r = 3.5 સેમી અને ઊંચાઈ h = 3 સેમી

3. 2 મી વ્યાસ અને 14 મી ઊંડાઈનો એક કૂવો ખોદીને તેમાંથી નીકળેલ માટી વડે કૂવાની આસપાસ 40 સેમી ઊંચાઈનો સપાટ ઘન કંકણાકાર ઓટલો બનાવવામાં આવે, તો તે ઓટલાની પહોળાઈ શોધો.


પાઠ્યપુસ્તકનાં ઉદાહરણો
12. શંકુના આડછેદના બે છેડાની ત્રિજ્યાઓ અનુક્રમે 28 સેમી અને 7 સેમી છે અને તેની ઊંચાઈ 45 સેમી છે. (જુઓ આકૃતિ) તેનું ઘનફળ, વક્રસપાટીનું ક્ષેત્રફળ અને કુલ ક્ષેત્રફળ શોધો.

શંકુનો આડછેદ એ ઊભા બે શંકુઓ OAB અને OCDનો તફાવત છે. (જુઓ આકૃતિ)
ધારો કે, શંકુ OAB ની ઊંચાઈ (સેમીમાં) h1 અને તિર્યક ઊંચાઈ l1 છે. તેથી OP = h1 અને OA = OB = l1.
ધારો કે, શંકુ OCDની ઊંચાઈ h2 અને તિર્યક ઊંચાઈ l2 છે. અહીં, r1 = 28 સેમી; r2 = 7 સેમી અને આડછેદની ઊંચાઈ (h) = 45 સેમી છે.
તેથી h1 = 45 + h2
સૌથી પહેલાં શંકુઓ OAB અને OCDની ઊંચાઈઓ અનુક્રમે h1 અને h2 નિશ્ચિત કરવી આવશ્યક છે.
બંને ત્રિકોણો OPB અને OQD સમરૂપ છે. (ખૂખૂ શરત)
(1) અને (2) ઉપરથી, h2 = 15 સેમી અને h1 = 60 સેમી મળશે.


13. હનુમપ્પા અને તેની પત્ની ગંગામ્મા શેરડીના રસમાંથી ગોળ બનાવે છે. તેમણે શેરડીના રસને ગરમ કરી રાબ બનાવેલી છે. તેને શંકુના આડછેદ આકારના નમૂનામાં નાખવામાં આવી છે. તેમાં બે વર્તુળાકાર સપાટીના વ્યાસ 30 સેમી અને 35 સેમી અને નમૂનાની શિરોલંબ ઊંચાઈ 14 સેમી છે. (જુઓ આકૃતિ) જો 1 સેમી રાબનું દળ 1.2 ગ્રામ હોય, તો પ્રત્યેક નમૂનામાં ભરી શકાય તેટલી રાબનું દ્રવ્યમાન શોધો.

14. એક ધાતુની ખુલ્લી ડોલ શંકુના આડછેદના આકારની છે અને તે એક ધાતુના ખુલ્લા નળાકારના આધાર પર છે. (જુઓ આકૃતિ) આ ડોલના બંને વર્તુળાકાર છેડાના વ્યાસ 45 સેમી અને 25 સેમી છે અને ડોલની કુલ શિરોલંબ ઊંચાઈ 40 સેમી છે. ખુલ્લી ડોલના પાયાના નળાકારની ઊંચાઈ 6 સેમી છે. આ ડોલ બનાવવા માટે કેટલા ક્ષેત્રફળવાળી ધાતુની શીટ જોઈએ તે શોધો. ડોલના હૅન્ડલની ગણતરી કરવામાં આવી નથી તથા તે ડોલમાં સમાઈ શકતા પાણીનું ઘનફળ કેટલું હશે તે પણ શોધો.


સ્વાધ્યાય – 13.4
1. 14 સેમી ઊંચાઈવાળા પીવાના પાણીનો પ્યાલો શંકુના આડછેદના આકારનો છે. બંને વર્તુળાકાર છેડાના વ્યાસ 4 સેમી અને 2 સેમી હોય, તો આ પ્યાલાની ક્ષમતા શોધો.

2. એક શંકુના આડછેદની તિર્યક ઊંચાઈ 4 સેમી છે તથા તેના વર્તુળાકાર છેડાની પરિમિતિ (પરિઘ) 18 સેમી અને 6 સેમી છે, તો શંકુના આડછેદની વક્રસપાટીનું ક્ષેત્રફળ શોધો.
આપેલ શંકુના આડછેદ માટે, તિર્યક ઊંચાઈ l = 4 સેમી, મોટા વર્તુળાકાર છેડાનો પરિઘ C1 = 18 સેમી અને નાના વર્તુળાકાર છેડાનો પરિઘ C2 = 6 સેમી

5. એક તુર્કી ટોપીનો આકાર શંકુના આડછેદ જેવો છે. (જુઓ આકૃતિ) જો તેની ખુલ્લી બાજુની ત્રિજ્યા 10 સેમી અને ઉપરની બાજુના વર્તુળની ત્રિજ્યા 4 સેમી હોય અને તિર્યક ઊંચાઈ 15 સેમી હોય, તો તેને બનાવવા માટે વપરાતા કાપડનું ક્ષેત્રફળ શોધો.

શંકુના આડછેદ આકારની તુર્કી ટોપી માટે, મોટી ત્રિજ્યા r1 = 10 સેમી, નાની ત્રિજ્યા r2 = 4 સેમી અને તિર્યક ઊંચાઈ l = 15 સેમી

4. એક વાસણ એક ધાતુની શીટમાંથી બનાવવામાં આવ્યું છે. તે ઉપરથી ખુલ્લું છે અને શંકુના આડછેદ જેવા આકારનું છે. તેની ઊંચાઈ 16 સેમી તથા બંને અંત્ય વર્તુળોની નીચેની અને ઉપરની ત્રિજ્યાઓ અનુક્રમે 8 સેમી અને 20 સેમી છે. દૂધથી સંપૂર્ણ ભરેલા વાસણમાં ₹ 20 પ્રતિ લિટર કિંમતવાળા આ વાસણમાં સમાઈ શકતા દૂધની કિંમત શોધો. આ વાસણ બનાવવા માટે વપરાયેલ ધાતુની શીટની કિંમત ₹ 8 પ્રતિ 100 સેમીના દરે શોધો. (π = 3.14 લો.)
શંકુના આડછેદ આકારના વાસણ માટે, મોટી ત્રિજ્યા r1 = 20 સેમી, નાની ત્રિજ્યા r2 = 8 સેમી અને ઊંચાઈ h =16 સેમી.


આમ, સંપૂર્ણ ભરેલા વાસણમાં સમાતા દૂધની કિંમત ₹ 209 થાય અને વાસણ બનાવવા માટે વપરાયેલ ધાતુની શીટની કિંમત ₹ 156.75 થાય.
5. ધાતુના લંબવૃત્તીય શંકુની ઊંચાઈ 20 સેમી તથા શિરોકોણ 60° છે. પાયાને સમાંતર સમતલથી તેના ઊંચાઈના બે સમાન ભાગ થાય તે રીતે કાપવામાં આવ્યો છે. જો આડછેદનું 1/16 સેમી વ્યાસવાળા તાર સ્વરૂપમાં રૂપાંતર કરવામાં આવે, તો તારની લંબાઈ શોધો.

અહીં, 20 સેમી ઊંચાઈ અને 60નો શિરોકોણ ધરાવતા લંબવૃત્તીય શંકુ OCDને પાયાને સમાંતર સમતલથી ઊંચાઈના બે સમાન ભાગ થાય તે રીતે કાપવામાં આવ્યો છે. એટલે કે, શિરોબિંદુ Oથી 10 સેમી અંતરેથી કાપીને શંકુ OAB તથા શંકુનો આડછેદ ACDB મેળવવામાં આવ્યા છે.



આમ, રૂપાંતર કરીને બનાવવામાં આવતા તારની લંબાઈ 7964.4 મી થાય.
1. એક ઘર્ષણ નિવારકનો આકાર શંકુના આડછેદ જેવો છે. તેની ત્રિજ્યાઓ અનુક્રમે 16 સેમી અને 10 સેમી છે તથા તેની ઊંચાઈ 8 સેમી છે. તેની વક્રસપાટીનું ક્ષેત્રફળ તેમજ તેનું ઘનફળ ના ગુણિતમાં શોધો.

આમ, ઘર્ષણ નિવારકની વક્રસપાટીનું ક્ષેત્રફળ 260 π સેમી2 અને તેનું ઘનફળ 1376 π સેમી3 થાય.
2. જો શંકુના આડછેદની તિર્યક ઊંચાઈ 20 સેમી અને ત્રિજ્યાઓ 20 સેમી અને 8 સેમી હોય, તો તેનું ઘનફળ શોધો. (π = 3.14 લો.)
આપેલ શંકુના આડછેદ માટે, તિર્યક ઊંચાઈ l = 20 સેમી, મોટી ત્રિજ્યા r1 = 20 સેમી અને નાની ત્રિજ્યા r2 = 8 સેમી

3. શંકુના આડછેદ આકારની એક ડોલની ત્રિજ્યાઓ 14 સેમી અને r સેમી છે, જ્યાં r < 14. જો ડોલની ઊંચાઈ 15 સેમી અને તેની ક્ષમતા 5.39 લિટર હોય, તો r ની કિંમત શોધો.
આપેલ શંકુના આડછેદ માટે, મોટી ત્રિજ્યા r1 = 14 સેમી, નાની ત્રિજ્યા r2 = r સેમી, ઊંચાઈ h = 15 સેમી અને ડોલની ક્ષમતા = 5.39 લિટર = 5390 સેમી3.


સ્વાધ્યાય – 13.5
* આ સ્વાધ્યાય પરીક્ષાના હેતુથી બનાવેલ નથી.
1. 3 મિમી વ્યાસવાળા તાંબાના તારને 12 સેમી ઊંચાઈ અને 10 સેમી વ્યાસવાળા નળાકાર પર એવી રીતે વીંટવામાં આવે છે કે નળાકારની વક્રસપાટી સંપૂર્ણપણે ઢંકાઈ જાય છે, તો તારની લંબાઈ અને દળ શોધો. તાંબાની ઘનતા 8.88 ગ્રામ / સેમી3 સ્વીકારવામાં આવી છે.
નળાકારની ઊંચાઈ = 12 સેમી = 120 મિમી
તારનો વ્યાસ ૩મિમી હોવાથી તારના એક આંટો નળાકારની ઊંચાઈમાંથી 3 મિમી જેટલા ભાગને ઢાંકી દેશે.
આથી નળાકારની વક્રસપાટીને સંપૂર્ણપણે ઢાંકી દેવા માટે તારના
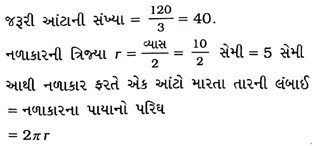

આમ, તારની લંબાઈ 1257.14 સેમી થાય અને તારનું દળ 789 ગ્રામ (આશરે) થાય.
2. એક કાટકોણ ત્રિકોણની બાજુઓ 3 સેમી અને 4 સેમી (કર્ણ સિવાયની બાજુઓ) છે. તેને તેના કર્ણ આસપાસ પરિભ્રમણ કરાવવામાં આવે છે. તેનાથી પ્રાપ્ત થતા બે શંકુનું ઘનફળ અને તેમની સપાટીનું ક્ષેત્રફળ શોધો. (πની કિંમત તમને અનુકૂળ પસંદ કરો.)


આમ, શંકુની જોડનું ઘનફળ 30.14 સેમી થાય અને તેની સપાટીનું ક્ષેત્રફળ 52.75 સેમી થાય.
3. એક ટાંકીનાં આંતરિક માપ 150 સેમી × 120 સેમી × 110 સેમી છે. તેમાં 129600 સેમી3 પાણી છે. ટાંકી પૂરેપૂરી ભરાય ન જાય ત્યાં સુધી તે પાણીમાં છિદ્રવાળી ઈંટો નાખવામાં આવે છે. પ્રત્યેક ઈંટ તેના 1/17 ઘનફળ જેટલું પાણી શોષી લે છે. પ્રત્યેક ઈંટનું માપ 22.5 સેમી × 7.5 સેમી × 6.5 સેમી છે, તો પાણી બહાર ન આવે તે રીતે તે ટાંકીમાં કેટલી ઈંટો નાખી શકાય?


આમ, પાણી બહાર ન આવે તે રીતે તે ટાંકીમાં 1792 ઈંટો નાખી શકાય.
4. આપેલા મહિનાના કોઈ એક પખવાડિયામાં એક નદીની ઘાટીમાં 10 સેમી વરસાદ પડ્યો છે. જો તે ઘાટીનું ક્ષેત્રફળ 7280 કિમી હોય, તો બતાવો કે કુલ વરસાદ લગભગ ત્રણ નદીઓના સામાન્ય પાણીના સરવાળા બરાબર હતો. પ્રત્યેક નદી 1072 કિમી લાંબી, 75 મીટર પહોળી અને ૩ મીટર ઊંડી છે.
1 કિમી2 = 1000000 મી2
એક પખવાડિયામાં નદીની ઘાટીમાં પડેલા વરસાદના પાણીનું કુલ ઘનફળ = ઘાટીનું ક્ષેત્રફળ × પડેલ વરસાદની ઊંચાઈ
= 7280 કિમી2 × 10 સેમી
= 7280000000 મી2 x 0.1 મી
= 728000000 મી3
= 0.728 કિમી3 ……. (1)
એક નદીમાં રહેતા સામાન્ય પાણીનું ઘનફળ
= 1072 કિમી × 75 મી × 3 મી
= 1072000 મી × 75 મી × 3 મી
= 241200000 મી3
∴ ત્રણ નદીમાં રહેતા સામાન્ય પાણીનું કુલ ઘનફળ
= 3 × 241200000 મી3
= 723600000 મી3
= 0.7236 કિમી3 ……. (2)
(1) અને (2)માં મેળવેલ કિંમતો લગભગ સમાન છે.
આમ, એક પખવાડિયામાં નદીની ઘાટીમાં પડેલ વરસાદનું પાણી લગભગ ત્રણ નદીઓના સામાન્ય પાણીના સરવાળા બરાબર હતો.
5. પતરાની એક ચીમની 10 સેમી લાંબા નળાકારના છેડે શંકુના આડછેદથી બનેલી છે. જો તેની કુલ ઊંચાઈ 22 સેમી હોય તથા નળાકાર ભાગનો વ્યાસ 8 સેમી અને ચીમનીના ઉપરના ભાગનો વ્યાસ 18 સેમી હોય, તો ચીમની બનાવવામાં વપરાતા પતરાનું ક્ષેત્રફળ શોધો. (જુઓ આકૃતિ)


હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
( 1 ) બે ગોલકની સપાટીના ક્ષેત્રફળનો ગુણોત્તર 1 : 4 છે, તો તેમના ઘનફળનો ગુણોત્તર ……… થાય.
( 2 ) બે સમઘન પૈકી દરેનું ઘનફળ 8 સેમી3 છે. આ બે સમઘનને એક-એક સપાટીથી જોડીને બનતા લંબઘનની કુલ સપાટીનું ક્ષેત્રફળ …… સેમી2 થાય.
( 3 ) જે સમઘનનું ઘનફળ 1728 સેમી3 હોય તેની ધારની લંબાઈ …… સેમી હોય.
( 4 ) બે શંકુના ઘનફળનો ગુણોત્તર 4:5 છે તથા તેમની ત્રિજ્યાઓનો ગુણોત્તર 2:3 છે. આથી તેમની ઊંચાઈનો ગુણોત્તર ……. થાય.
( 5 ) 7 સેમી ત્રિજ્યા અને 25 સેમી તિર્યક ઊંચાઈ ધરાવતા શંકુનું ઘનફળ …….. સેમી3 થાય.
( 6 ) 3 સેમી ત્રિજ્યાવાળા સફરજનની કિંમત ₹ 8 છે, તો 6 સેમી ત્રિજ્યાવાળા સફરજનની કિંમત ……. થાય.
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
( 1 ) 3 સેમી, 4 સેમી અને 5 સેમી ત્રિજ્યાવાળા ધાતુના ત્રણ ગોલક ઓગાળીને એક મોટો ગોલક બનાવવામાં આવે, તો તે ગોલકની ત્રિજ્યા …… સેમી થાય.
A. 4
B. 12
C. 6
D. 8
( 2 ) r ત્રિજ્યાવાળા અર્ધગોલકમાંથી કોતરીને બનાવેલ શંકુનું મહત્તમ ઘનફળ ……. થાય.
(3) જેની ધાર વ હોય તેવા એક સમઘનમાંથી મહત્તમ ઘનફળ ધરાવતો નળાકાર કોતરવામાં આવે, તો તે નળાકારનું ઘનફળ ……. થાય.
( 4 ) 6 સેમી ત્રિજ્યા અને 10 સેમી ઊંચાઈવાળી નળાકાર બાટલીમાં રહેલું પ્રવાહી 2 સેમી ત્રિજ્યા અને 3.6 સેમી ઊંચાઈવાળા શંકુ આકારનાં પાત્રોમાં ભરવામાં આવે, તો …….. પાત્રો ભરી શકાય.
A. 100
B. 25
C. 75
D. 20
( 5 ) બે ગોલકની સપાટીના ક્ષેત્રફળનો ગુણોત્તર 1 : 2 છે. આથી તેમના નળનો ગુણોત્તર ……… થાય.
A. √2 : 1
B 1 : 2√2
C. 1 : 8
D. 1 : 4
( 6 ) બે નળાકારની ત્રિજ્યાનો ગુણોત્તર 23 અને ઊંચાઈનો ગુણોત્તર 5 : 3 હોય, તો તેમના નળનો ગુણોત્તર …… થાય.
A. 27 : 20
B. 20 : 27
C. 9 : 4
D. 4: 9
( 7 ) 9 સેમી અને 10 સેમી ત્રિજ્યાવાળા ધાતુના બે ગોલકો ઓગાળીને તેમાંથી બે નવા ગોલકો બનાવ્યા છે. જો નવા ગોલકો પૈકી એક ગોલકની ત્રિજ્યા 12 સેમી હોય, તો બીજા ગોલકની ત્રિજ્યા …… સેમી હોય.
A. 7
B. 5
C. 3
D. 1
( 8 ) r ત્રિજ્યાવાળા ગોલની સપાટીનું ક્ષેત્રફળ S1 હોય અને r ત્રિજ્યા અને 2r ઊંચાઈવાળા નળાકારની કુલ સપાટીનું ક્ષેત્રફળ S2 હોય, તો …… સાચું છે.
A. S1 = S2
B. S1 > S2
C. S1 < S2
D. S1 = 2S2
( 9 ) 6 સેમી વ્યાસ અને 32 સેમી ઊંચાઈવાળા ધાતુના નળાકારને ઓગાળીને તેમાંથી એકસરખા માપના 8 ગોલક બનાવવામાં આવે, તો તે દરેક ગોલકનો વ્યાસ સેમી થાય.
A. 3
B. 6
C. 12
D. 8
(10) સમાન ઊંચાઈ h સેમી ધરાવતા ધાતુના બે શંકુઓની ત્રિજ્યા r1 સેમી અને r2 સેમી છે. તે બે શંકુઓને ઓગાળીને h સેમી ઊંચાઈવાળો એક નળાકાર બનાવવામાં આવે, તો તે નળાકારની ત્રિજ્યા ……. સેમી થાય.

(11) આકૃતિમાં દર્શાવ્યા મુજબ રમકડાનું કુલ પૃષ્ઠફળ ……… છે.

3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ લખો :
( 1 ) બે ગોલકના ઘનફળનો ગુણોત્તર 64 : 27 છે. તેમના ક્ષેત્રફળનો ગુણોત્તર શોધો.
( 2 ) એક નળાકારનો વ્યાસ 28 સેમી અને ઊંચાઈ 21 સેમી છે. તેની વક્રસપાટીનું ક્ષેત્રફળ શોધો.
( 3 ) જો ગોલની ત્રિજ્યાના માપમાં 20% વધારો કરવામાં આવે, તો તેના ઘનળના માપમાં કેટલા ટકા વધારો થાય?
( 4 ) એક નળાકાર અને એક શંકુની ત્રિજ્યાઓ સમાન છે તથા ઊંચાઈ પણ સમાન છે. નળાકારના ઘનળ અને શંકુના ઘનફળનો ગુણોત્તર શોધો.
( 5 ) એક લંબઘનની પાસપાસેની ત્રણ સપાટીઓના ક્ષેત્રફળ X, Y અને Z છે. લંબઘનનું ઘનફળ શોધો.
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) a ધાર હોય તેવા બે એકસમાન સમઘનને કોઈ સપાટીથી જોડતાં બનતા લંબઘનની કુલ સપાટીનું ક્ષેત્રફળ 12a2 થાય.
( 2 ) ધાતુના એક ગોલકને ઓગાળીને તેમાંથી 8 એકસરખા નવા ગોલક બનાવવામાં આવે, તો દરેક નવા ગોલકની ત્રિજ્યા મુળ ગોલકની ત્રિજ્યા કરતાં 1/8 ભાગની થાય.
( 3 ) r સેમી ત્રિજ્યા ધરાવતા બે એકસમાન અર્ધગોલકોને તેમના પાયાથી જોડતાં બનતા ઘનાકારની કુલ સપાટીનું ક્ષેત્રફળ 6 π r2 સેમી2 થાય.
( 4 ) a ધારવાળી સમઘન પેટીમાં બરાબર બંધબેસતા ગોલકનું ઘનફળ 1/6 π a3 થાય.
( 5 ) શંકુના આડછેદનું ઘનફળ = 1/3 π h (r12 + r22 – r1r2), જ્યાં h એ આડછેદની ઊંચાઈ છે તથા r1 અને r2 એ આડછેદના વર્તુળાકાર છેડાઓની ત્રિજ્યા છે.

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here