Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 14 Statistics (આંકડાશાસ્ત્ર)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 14 Statistics (આંકડાશાસ્ત્ર)સ્વાધ્યાય – 14.1
1. વિદ્યાર્થીઓના એક સમૂહ દ્વારા તેમના પર્યાવરણ જાગૃતિ કાર્યક્રમના ભાગરૂપે એક સર્વેક્ષણ હાથ ધરવામાં આવ્યું. તેમાં તેમણે એક વિસ્તારના 20 ઘરોમાં વનસ્પતિના છોડની સંખ્યા વિશે નીચેની માહિતી એકઠી કરી. ઘરદીઠ છોડની સંખ્યાઓનો મધ્યક શોધો.
મધ્યક શોધવા માટે કઈ રીતનો ઉપયોગ કરશો અને શા માટે?
2. એક ફૅક્ટરીમાં 50 કારીગરોના દૈનિક વેતનના નીચે આપેલ વિતરણનો વિચાર કરો :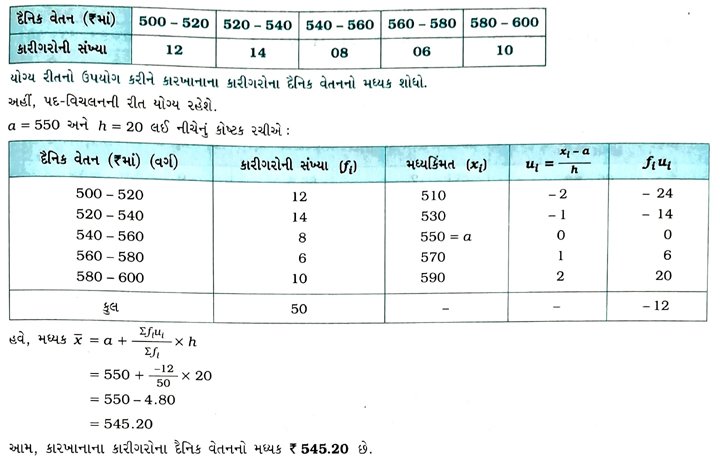
3. નીચેનું આવૃત્તિ-વિતરણ વસતીનાં બાળકોનું દૈનિક ખિસ્સાભથ્થું દર્શાવે છે. ખિસ્સાભથ્થાનો મધ્યક ₹ 18 છે. ખૂટતી આવૃત્તિ ƒ શોધો.
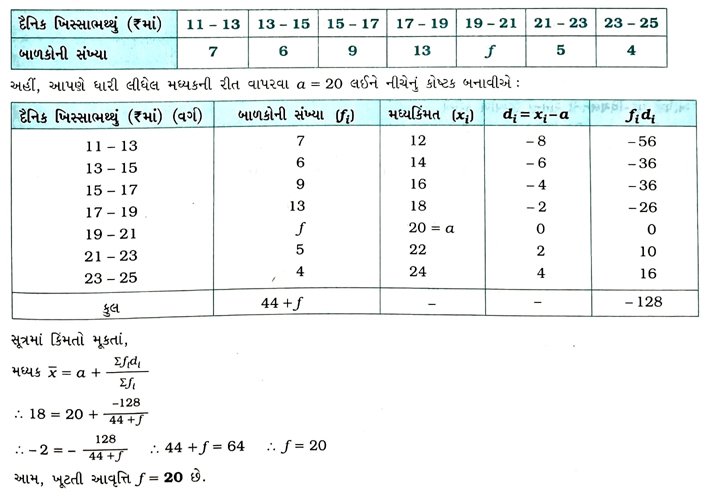4. એક હૉસ્પિટલમાં દાક્તરે ત્રીસ મહિલાઓની શારીરિક તપાસ અને પ્રતિમિનિટ હૃદયના ધબકારાની નોંધ કરી તથા નીચે પ્રમાણે સારાંશ તૈયાર કર્યો. યોગ્ય રીત પસંદ કરીને, આ મહિલાઓના પ્રતિમિનિટ હૃદયના ધબકારાનો મધ્યક શોધો.
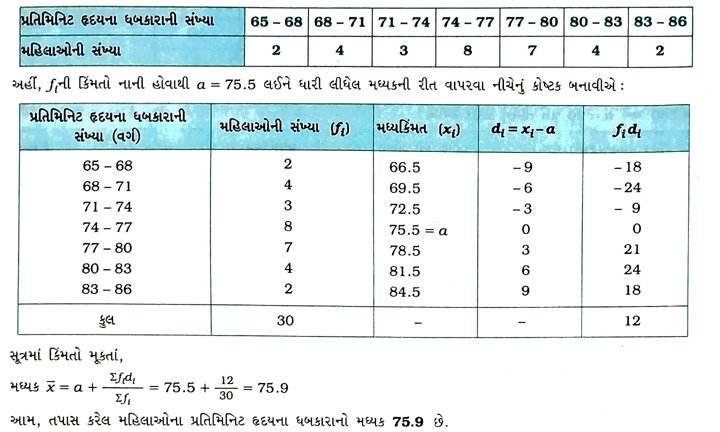5. એક છૂટક વેચાણ બજારમાં, ફળ વેચનારાઓ બંધ ખોખાંઓમાં કેરીઓ વેચી રહ્યા હતા. આ ખોખાંઓમાં કેરીઓ જુદી જુદી સંખ્યાઓમાં હતી. ખોખાંઓની સંખ્યાનાં પ્રમાણ કેરીઓનું આવૃત્તિ-વિતરણ નીચે પ્રમાણે હતું :
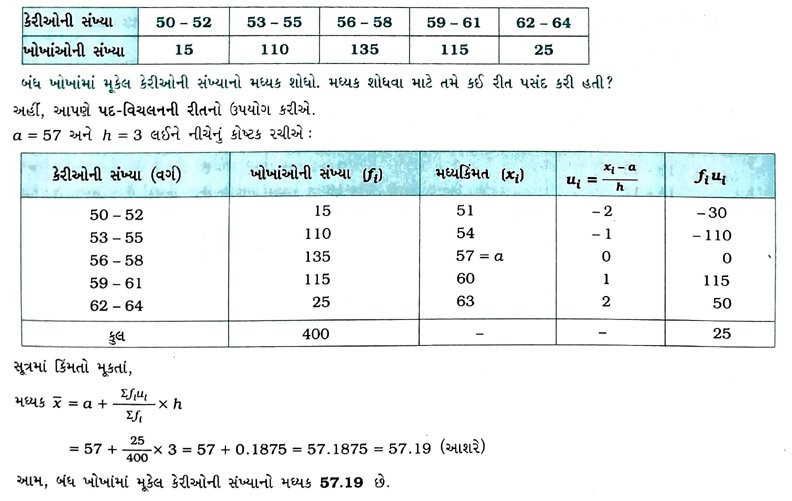6. નીચેનું કોષ્ટક એક વિસ્તારમાં 25 પરિવારના ખોરાકનો દૈનિક ઘરગથ્થુ ખર્ચ બતાવે છે :
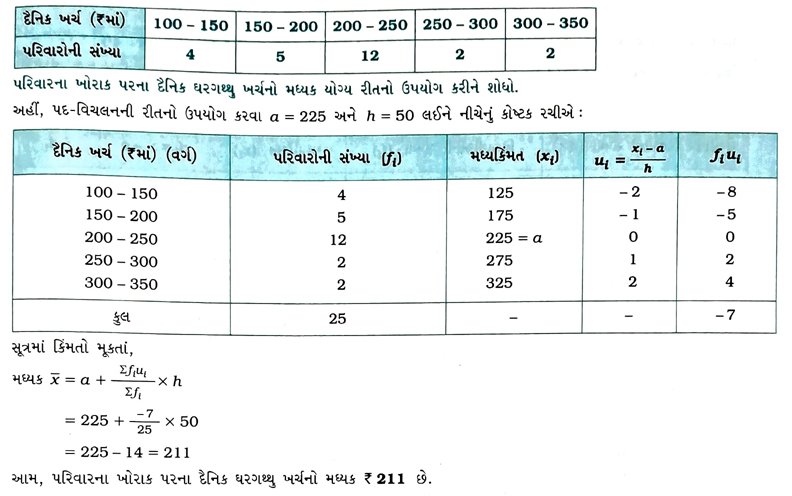7. એક ચોક્કસ શહેરમાં 30 વિસ્તારોમાં હવામાં SO2ની સાંદ્રતા (ઘટકો પ્રતિ દસ લાખમાં, એટલે કે ppmમાં) શોધવા માટે નીચે દર્શાવેલ માહિતી એકત્રિત કરવામાં આવી હતી :
8. એક વર્ગના સમગ્ર સત્રની 40 વિદ્યાર્થીઓની ગેરહાજરીની યાદી વર્ગશિક્ષક પાસે છે. વિદ્યાર્થીઓની ગેરહાજર દિવસોની સંખ્યાનો મધ્યક શોધો.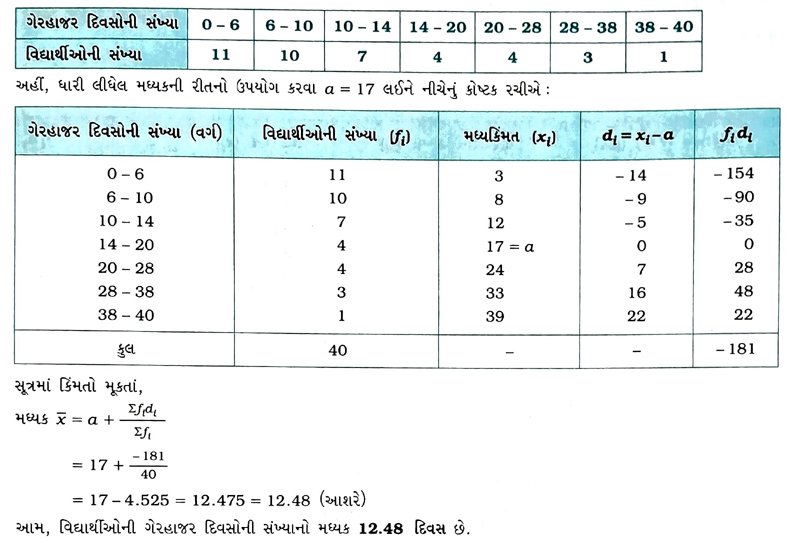
9. નીચેનું કોષ્ટક 35 શહેરોમાં સાક્ષરતા દર (પ્રતિશતમાં) આપે છે. સાક્ષરતા દરનો મધ્યક શોધો.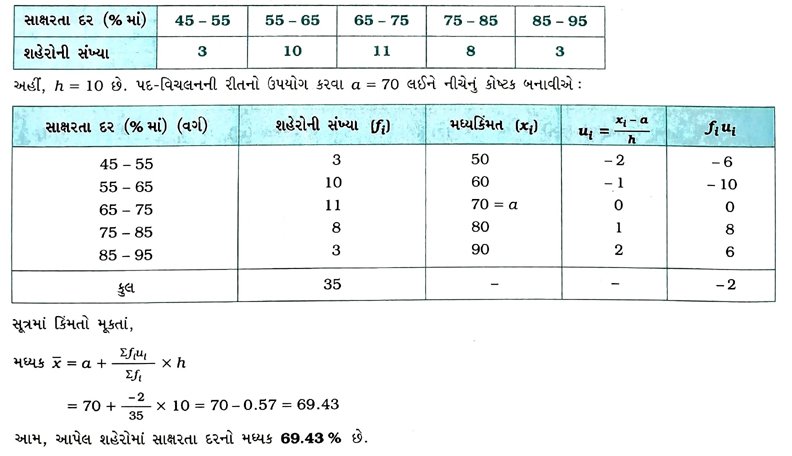
મહત્ત્વનાં અન્ય ઉદાહરણો
1. એક શાળાના બે વર્ગના 100 વિદ્યાર્થીઓએ ગણિતના 100 ગુણના પ્રશ્નપત્રમાં મેળવેલા ગુણ નીચેના કોષ્ટકમાં આપેલા છે :
સીધી રીતે વિદ્યાર્થીઓએ મેળવેલા ગુણનો મધ્યક શોધો. ત્યારબાદ માહિતીનું 10 – 25, 25 – 40, …. 85 – 100 વર્ગોમાં વર્ગીકરણ કરીને ત્રણેય રીતે મધ્યક શોધો.
( 1 ) સીધી રીત :
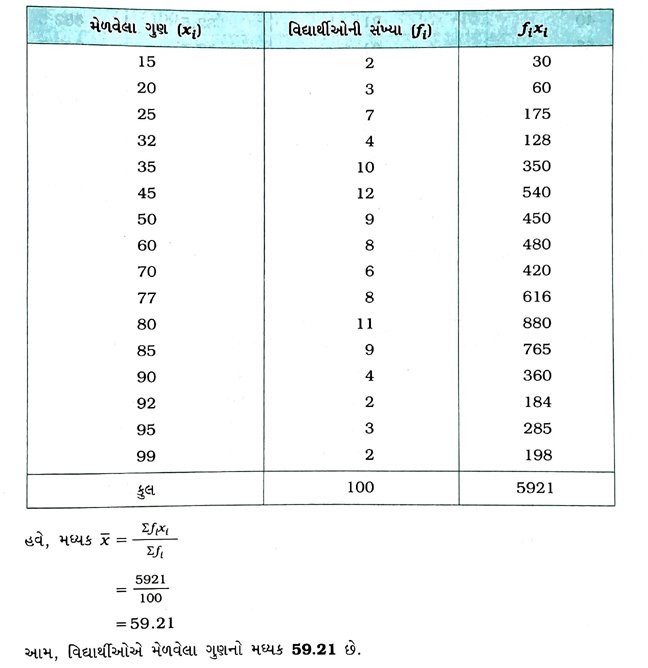
( 2 ) વર્ગીકૃત માહિતી માટે સીધી રીતઃ
માહિતીનું વર્ગીકરણ 10-25, 25-40, ….. 85–100 વર્ગો લઈને કરતાં નીચે મુજબનું આવૃત્તિ-વિતરણ મળે :
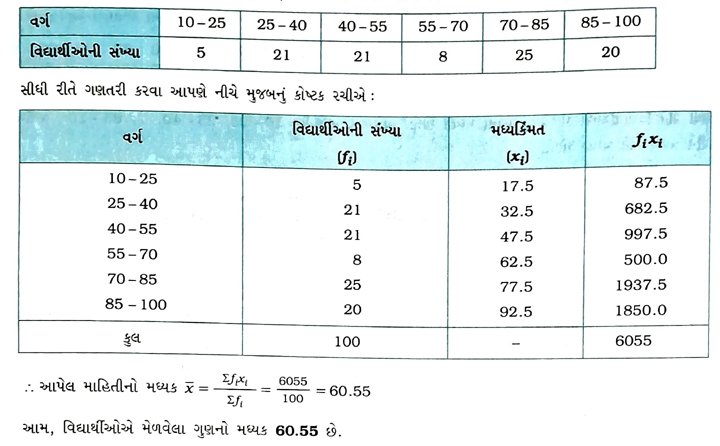
( 3 ) ધારી લીધેલ મધ્યકની રીત :
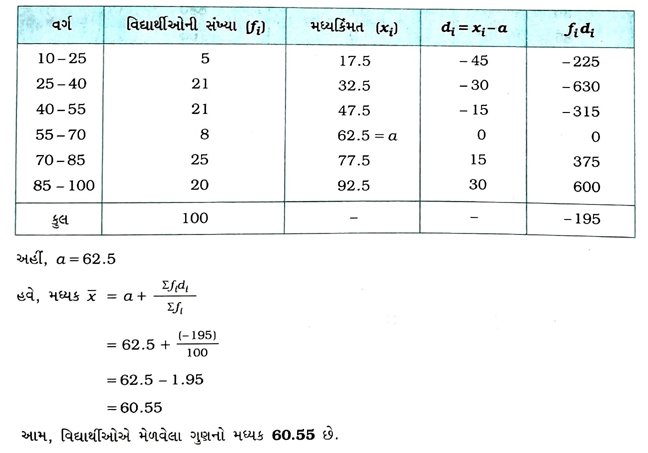
( 4 ) પદ-વિચલનની રીત :
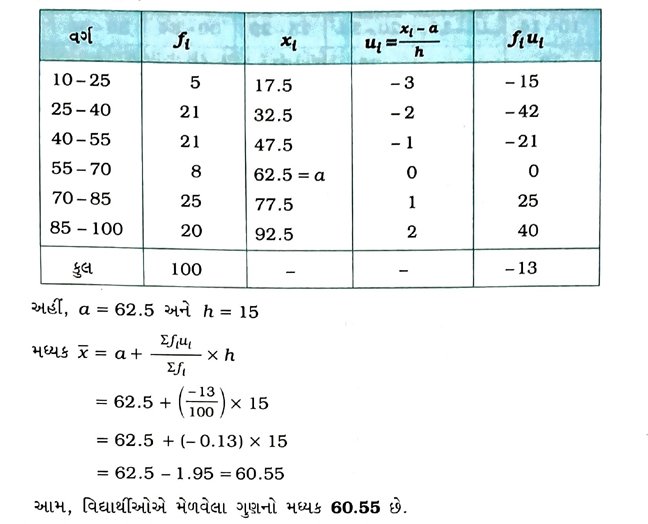
2. નીચે આપેલ આવૃત્તિ-વિતરણનો મધ્યક ત્રણેય રીતે શોધો :
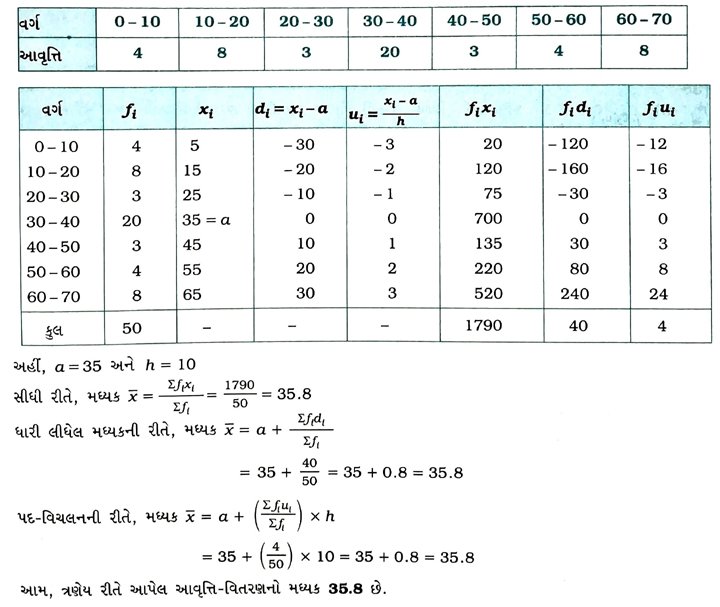
3. 125 અવલોકનો ધરાવતા નીચે આપેલ આવૃત્તિ-વિતરણનો મધ્યક 22.12 છે, તો ખૂટતી આવૃત્તિઓ શોધો :
ધારો કે, વર્ગ 15 – 19ની આવૃત્તિ ƒ1 અને વર્ગ 30–34ની આવૃત્તિ ƒ2 છે. a = 17 અને h = 5 લઈને પદ-વિચલનની રીતનો ઉપયોગ કરીએ.
સ્વાધ્યાય – 14.2
1. નીચેનું કોષ્ટક એક વર્ષ દરમિયાન એક દવાખાનામાં દાખલ થયેલા દર્દીઓની ઉંમર દર્શાવે છે :
ઉપર આપેલ માહિતી માટે બહુલક અને મધ્યક શોધો. કેન્દ્રીય મધ્યવર્તી સ્થિતિનાં આ બે માપોની સરખામણી અને અર્થઘટન કરો.
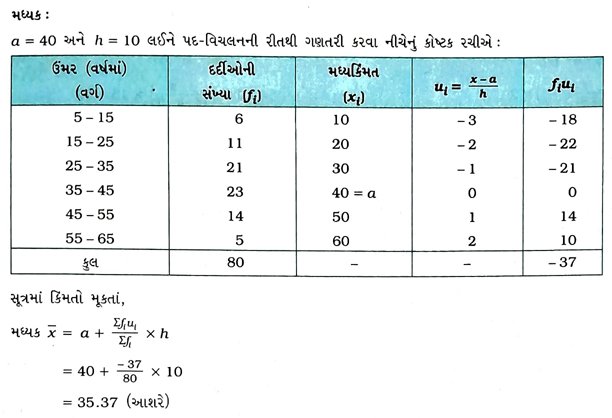
આમ, આપેલ માહિતીનો બહુલક 36.8 વર્ષ છે અને મધ્યક 35.37 વર્ષ છે.
અર્થઘટન : ઉ૫૨ મેળવેલાં પરિણામો દર્શાવે છે કે દવાખાનામાં દાખલ થયેલ દર્દીઓ પૈકી મહત્તમ સંખ્યાના દર્દીઓની ઉંમર 36.8 વર્ષ છે અને દાખલ થયેલ બધા જ દર્દીઓની સરેરાશ ઉંમર 35.37 વર્ષ છે.
2. નીચેની માહિતી 225 વીજઉપકરણોના આયુષ્યની (કલાકોમાં) પ્રાપ્ત માહિતી દર્શાવે છે :
3. નીચેની માહિતી એક ગામનાં 200 કુટુંબો માટે તેમના ઘર ચલાવવા માટે કુલ માસિક ખર્ચનું આવૃત્તિ-વિતરણ દર્શાવે છે. કુટુંબોના માસિક ખર્ચનો બહુલક શોધો તથા કુટુંબોના માસિક ખર્ચનો મધ્યક શોધો.
4. નીચેનું વિતરણ ભારતની ઉચ્ચતર માધ્યમિક શાળાઓમાં રાજ્યવાર શિક્ષક-વિદ્યાર્થી ગુણોત્તરનું વિતરણ આપે છે. આ માહિતીનો બહુલક અને મધ્યક શોધો. આ બે માપનું અર્થઘટન કરો.
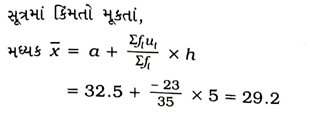
આમ, આપેલ માહિતીનો બહુલક 30.6 અને મધ્યક 29.2 છે.
અર્થઘટન : ઉપરોક્ત પરિણામો દર્શાવે છે કે મોટા ભાગનાં રાજ્યો / કેન્દ્રશાસિત પ્રદેશોમાં શિક્ષકદીઠ વિદ્યાર્થીઓની સંખ્યા 30.6 છે અને શિક્ષકદીઠ સરેરાશ વિદ્યાર્થીઓની સંખ્યા 29.2 છે.
5. નીચે આપેલ આવૃત્તિ-વિતરણ વિશ્વના કેટલાક શ્રેષ્ઠ બૅટ્સમૅનો દ્વારા એક- દિવસીય આંતરરાષ્ટ્રીય મૅચોમાં નોંધાવેલ રનની સંખ્યા આપે છે :
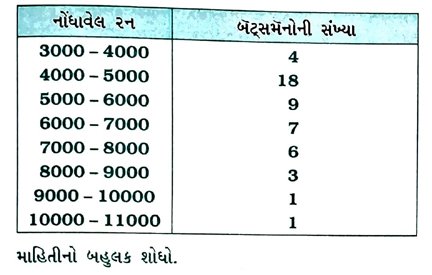
અહીં, મહત્તમ આવૃત્તિ 18 એ વર્ગ 4000 – 5000ની આવૃત્તિ હોવાથી વર્ગ 4000 – 5000 એ બહુલક વર્ગ છે.
6. એક વિદ્યાર્થીએ પ્રત્યેક 8 મિનિટનો એક, એવા 100 સમયગાળાઓ માટે રસ્તા પરની એક જગ્યાએથી પસાર થતી ગાડીઓની સંખ્યાની નોંધ કરી અને તેને નીચે આપેલ કોષ્ટકમાં સંક્ષિપ્ત સ્વરૂપમાં દર્શાવી છે. આ માહિતીનો બહુલક શોધો.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. 100 દુકાનોના દૈનિક નફાની માહિતી એકત્ર કરતાં નીચે મુજબનું કોષ્ટક મળે છે :
2. નીચે આપેલ 165 અવલોકનો ધરાવતાં આવૃત્તિ-વિતરણનો બહુલક 34.5 છે :
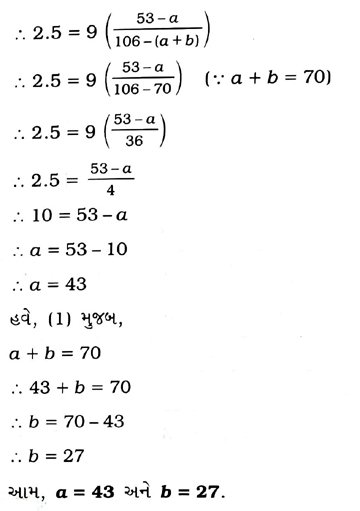
સ્વાધ્યાય – 14.3
1. નીચેનું આવૃત્તિ-વિતરણ એક વિસ્તારમાં 68 ગ્રાહકોનો માસિક વીજવપરાશ આપે છે. આ માહિતીનો મધ્યસ્થ, મધ્યક અને બહુલક શોધો અને તેમને સરખાવો.
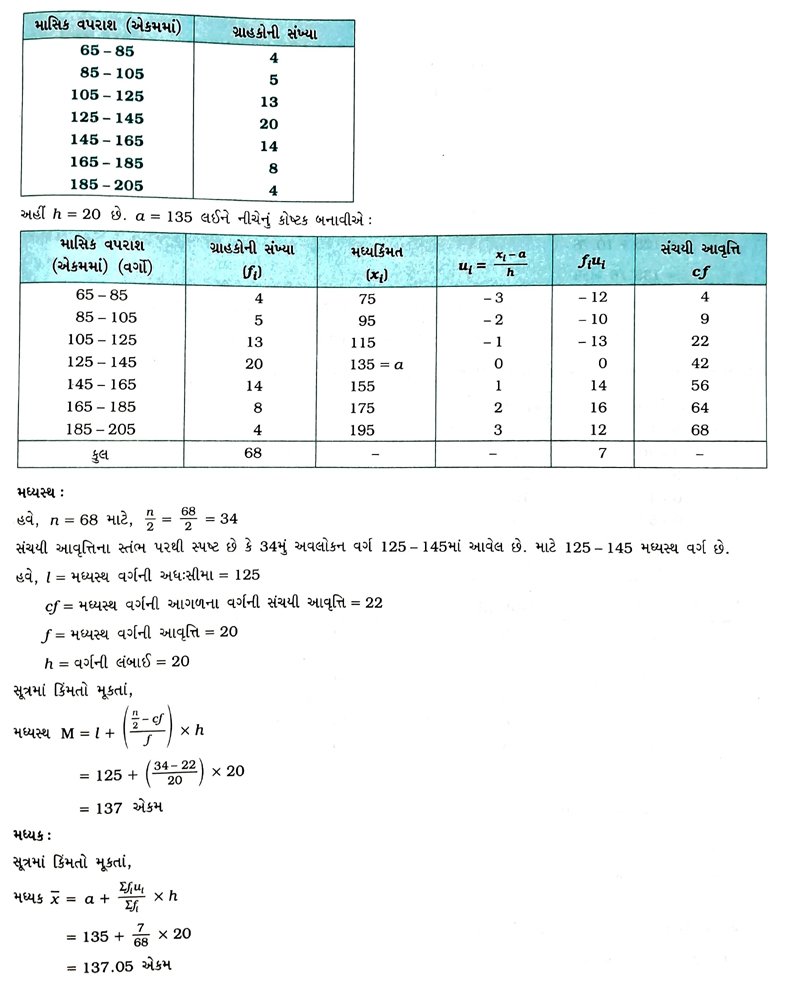
આમ, માહિતીનો મધ્યસ્થ, મધ્યક અને બહુલક અનુક્રમે 137 એકમ, 137.05 એકમ અને 135.76 એકમ છે.
સરખામણી : મધ્યવર્તી સ્થિતિમાનનાં ત્રણેય માપની સરખામણી કરતાં જણાય છે કે તે ત્રણેયની કિંમત લગભગ સમાન છે.
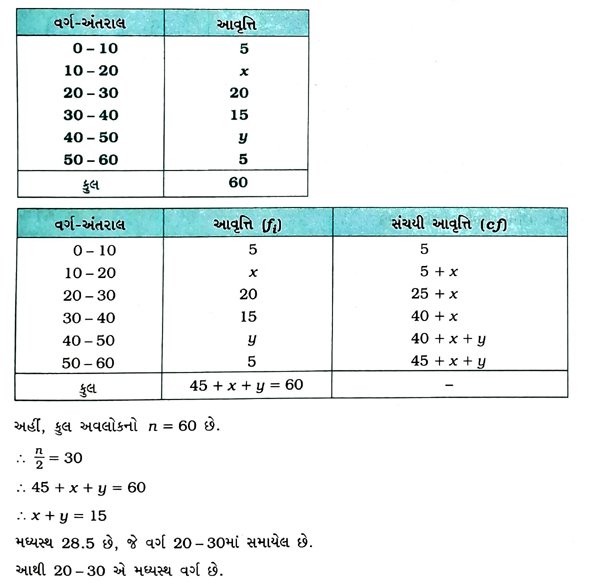
2. જો નીચે આપેલ આવૃત્તિ-વિતરણનો મધ્યસ્થ 28.5 હોય, તો x અને પુનાં મૂલ્યો શોધો :
3. એક જીવનવીમા એજન્ટે, 100 પૉલિસી-ધારકોની ઉંમર માટે નીચેનું વિતરણ પ્રાપ્ત કર્યું. જેમની ઉંમર 18 વર્ષથી વધુ, પરંતુ 60 વર્ષથી ઓછી હોય તેવી જ વ્યક્તિઓને પૉલિસીઓ આપવામાં આવી હોય, તો તેમની મધ્યસ્થ ઉંમર શોધો.
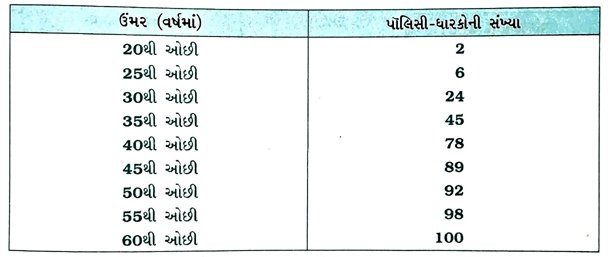
અહીં, આપેલ આવૃત્તિ-વિતરણ ‘થી ઓછા’ પ્રકારનું આવૃત્તિ-વિતરણ છે. તે પરથી નીચે પ્રમાણેનું સતત આવૃત્તિ-વિતરણ સહેલાઈથી મળે. પૉલિસી 18 વર્ષથી વધુ ઉંમરવાળી વ્યક્તિઓને આપવામાં આવે છે. તેથી પ્રથમ વર્ગ 18–20 થશે.
આમ, પૉલિસી-ધારકોની મધ્યસ્થ ઉંમર 35.76 વર્ષ છે.
[નોંધઃ અહીં, પ્રથમ વર્ગની વર્ગલંબાઈ બીજા વર્ગોની વર્ગલંબાઈથી અલગ પડે છે. તેથી સૂત્ર વાપરવાની શરતનું પાલન થતું નથી. પરંતુ મધ્યસ્થની કિંમત પર છેડાની કિંમતો(ખૂબ નાની અથવા ખૂબ મોટી કિંમતો)ની ખાસ અસર પડતી ન હોવાથી, આપણે સૂત્રનો ઉપયોગ કરી શકીએ છીએ.]
4. એક છોડનાં 40 પાંદડાઓની લંબાઈ ખૂબ જ નજીકના મિલિમીટર સુધી માપવામાં આવી અને મેળવેલ માહિતી નીચેના કોષ્ટકમાં દર્શાવી છે :
| લંબાઈ (મિમીમાં) | પાંદડાઓની સંખ્યા |
|
118-126
127-135
136-144
145-153
154-162
163-171
172-180
|
3
5
9
12
5
4
2
|
પાંદડાઓની મધ્યસ્થ લંબાઈ શોધો.
[સૂચન: મધ્યસ્થ શોધવા માટે માહિતીને સતત વર્ગોમાં ફેરવવાની જરૂર છે, કારણ કે સૂત્ર સતત વર્ગો માટે છે. પછી વર્ગો 117.5-126.5, 126.5-135.5, ……. 171.5 – 180.5માં પરિવર્તિત થાય છે.]
માહિતીને સતત વર્ગોમાં ફેરવીને નીચેનું કોષ્ટક બનાવીએ :
5. નીચેનું કોષ્ટક 400 નિઓન ગોળાના આયુષ્યનું આવૃત્તિ-વિતરણ આપે છે :
6. સ્થાનિક ટેલિફોન યાદીમાંથી 100 અટક યાદચ્છિક રીતે પસંદ કરવામાં આવી હતી અને અંગ્રેજી મૂળાક્ષરોમાં અટકોમાં આવતા અક્ષરોની સંખ્યાનું આવૃત્તિ-વિતરણ નીચે પ્રમાણે મેળવ્યું હતું :
અટકોમાં આવતા અક્ષરોની સંખ્યાનો મધ્યસ્થ શોધો. અટકોમાં આવતા અક્ષરોની સંખ્યાનો મધ્યક પણ શોધો. અટકોમાં આવતા અક્ષરોની સંખ્યાનો બહુલક શોધો.
અહીં, h = 3 છે. a = 8.5 લઈને નીચેનું કોષ્ટક બનાવીએ :
આમ, અટકોમાં આવતા અક્ષરોની સંખ્યાનો મધ્યસ્થ 8.05 અક્ષરો, મધ્યક 8.32 અક્ષરો અને બહુલક 7.88 અક્ષરો છે.
7. નીચેનું વિતરણ એક ધોરણના 30 વિદ્યાર્થીઓનાં વજન આપે છે. વિદ્યાર્થીઓના વજનનો મધ્યસ્થ શોધો.
મહત્ત્વનાં અન્ય ઉદાહ૨ણો
1. નીચે આપેલા આવૃત્તિ-વિતરણ પરથી p અને વૃની કિંમતો શોધો. ત્યારબાદ મધ્યક વર્ગ તથા બહુલક વર્ગ પણ શોધો.
40મું અવલોકન વર્ગ 400 – 500માં સમાયેલ હોવાથી 400 – 500 મધ્યસ્થ વર્ગ છે.
મહત્તમ આવૃત્તિ 20 એ વર્ગ 500 – 600ની આવૃત્તિ હોવાથી 500 – 600 એ બહુલક વર્ગ છે.
આમ, P = 23, q = 13, મધ્યસ્થ વર્ગ 400-500 અને બહુલક વર્ગ 500 – 600 છે.
2. નીચેના આવૃત્તિ-વિતરણ માટે, જો n = 100 અને મધ્યસ્થ = 32 હોય, તો ખૂટતી આવૃત્તિઓ ƒ1 અને ƒ2 શોધો :
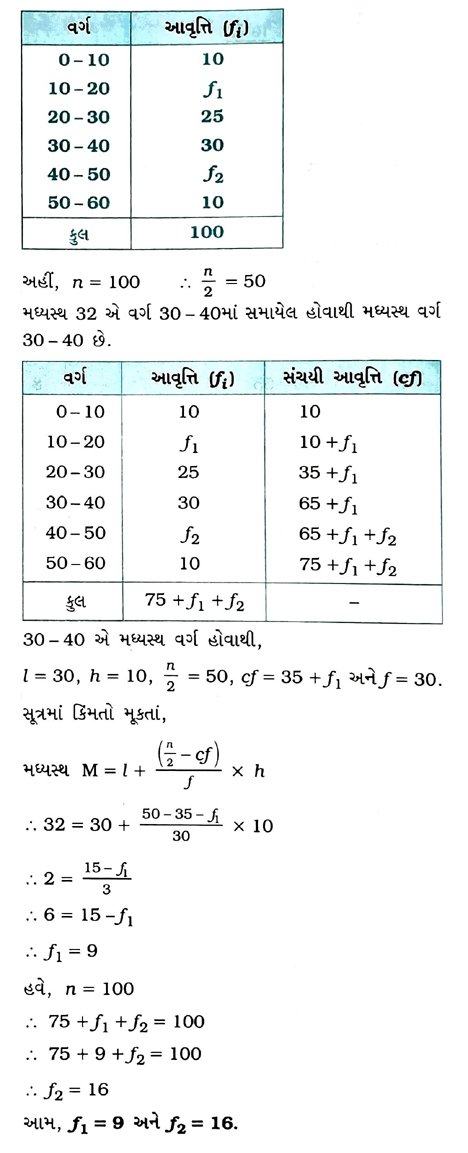
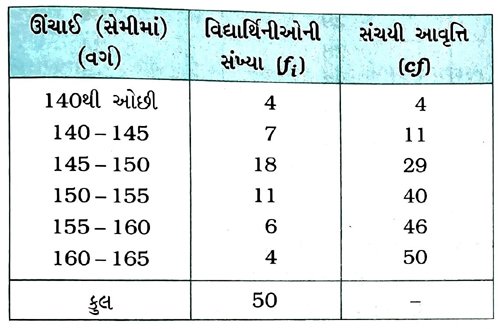
3. એક શાળાની 50 વિદ્યાર્થિનીઓની ઊંચાઈ (સેમીમાં) નીચે દર્શાવેલ કોષ્ટકમાં રજૂ કરેલ છે :
વિદ્યાર્થિનીઓની ઊંચાઈનો મધ્યસ્થ શોધો.
આપેલ ‘થી ઓછા’ પ્રકારના સંચયી આવૃત્તિ-વિતરણ પરથી નીચે મુજબનું સતત આવૃત્તિ-વિતરણ સહેલાઈથી મળે:
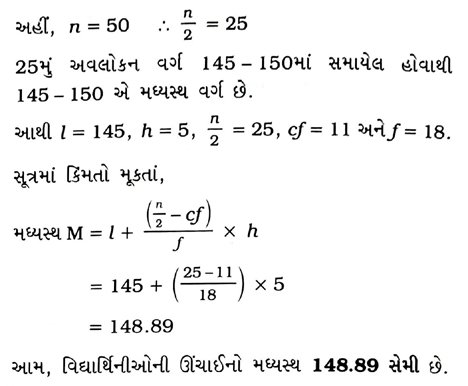
સ્વાધ્યાય – 14.4
1. નીચેનું આવૃત્તિ-વિતરણ એક કારખાનાના 50 કર્મીઓનું દૈનિક વેતન દર્શાવે છે :
ઉપરના આવૃત્તિ-વિતરણને, ‘થી ઓછા’ પ્રકારના સંચયી આવૃત્તિ-વિતરણમાં ફેરવો અને તેનો ‘ઓજાઈવ’ દોરો.
‘થી ઓછા’ પ્રકારનું સંચયી આવૃત્તિ-વિતરણ :
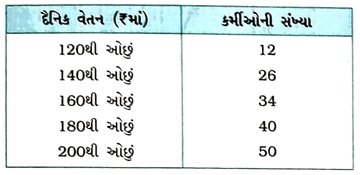
હવે, બિંદુઓ (120, 12), (140, 26), (160, 34), (180, 40) અને (200, 50)નું આલેખન કરીને તે બધાં જ બિંદુઓને મુક્તહસ્ત વક્ર દ્વારા જોડીને ‘થી ઓછા’ પ્રકારનો ઓજાઈવ મેળવીએ.
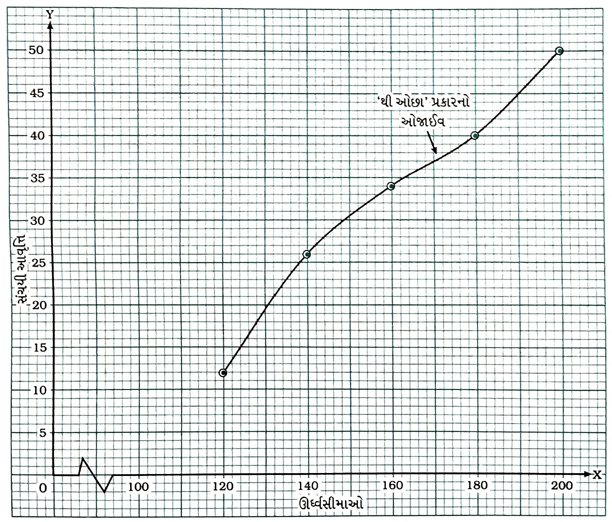
2. એક વર્ગના 35 વિદ્યાર્થીઓની દાક્તરી તપાસ દરમિયાન, તેમનાં વજન નીચે પ્રમાણે નોંધાયા :
આપેલ માહિતી માટે ‘થી ઓછા’ પ્રકારનો ઓજાઈવ દોરો. તે પરથી વજનનો મધ્યસ્થ મેળવો. આલેખ પરથી આ મેળવેલા પરિણામને સૂત્રનો ઉપયોગ કરીને ચકાસો.
‘થી ઓછા’ પ્રકારનો ઓજાઈવ દોરવા માટે આપણે બિંદુઓ (38, 0), (40, 3), (42, 5), (44, 9), (46, 14), (48, 28), 50, 32) અને (52, 35)નું નિરૂપણ કરીએ અને ત્યારબાદ તે બધાં જ બિંદુઓને સળંગ મુક્તહસ્ત વક્ર દ્વારા જોડીએ.
હવે, મધ્યસ્થ શોધવા માટે, પુ-અક્ષના બિંદુ (0, 17.5)માંથી x-અક્ષને સમાંતર રેખા દોરીએ જે ઓજાઈવને બિંદુ માં છેદે. બિંદુ Pનો x-યામ મધ્યસ્થની કિંમત આપે છે.
ઓજાઈવ પરથી સ્પષ્ટ છે કે, બિંદુ Pનો x-યામ 46.5 છે. આથી મધ્યસ્થની કિંમત 46.5 છે.
3. નીચેનું કોષ્ટક એક ગામનાં 100 ખેતરોમાં પ્રતિહેક્ટર ઘઉંનું ઉત્પાદન દર્શાવે છેઃ
આ આવૃત્તિ-વિતરણને ‘થી વધુ’ પ્રકારના વિતરણમાં પરિવર્તિત કરો અને તેનો ઓજાઈવ દોરો.
‘થી વધુ’ પ્રકારનો ઓજાઈવ દોરવા આપણે બિંદુઓ (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) (75, 16)નું નિરૂપણ કરીએ અને ત્યારબાદ તે બધાં જ બિંદુઓને સળંગ મુક્તહસ્ત વક્ર વડે જોડીએ.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. 101 વિદ્યાર્થીઓએ એક પરીક્ષામાં મેળવેલ ગુણનું આવૃત્તિ- વિતરણ નીચે પ્રમાણે છે :
આપેલ માહિતી માટે બંને પ્રકારના ઓજાઈવ દોરો અને તે પરથી વિદ્યાર્થીઓએ મેળવેલ ગુણનો મધ્યસ્થ શોધો.
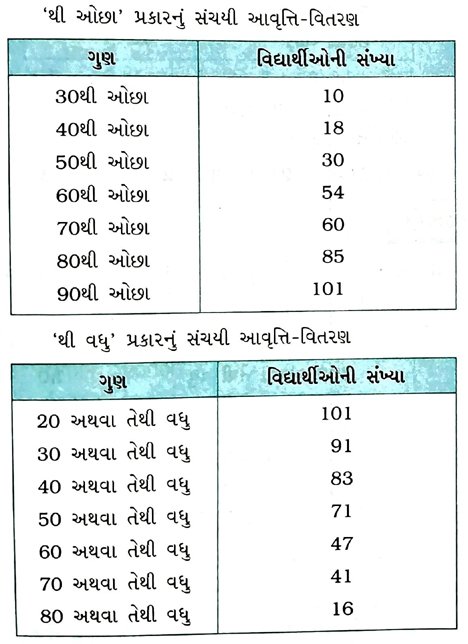
આલેખ પરથી જણાય છે કે બંને પ્રકારના ઓજાઈવ પરસ્પર P બિંદુએ છેદે છે અને બિંદુ Pનો x-યામ 58 છે.
આથી આપેલ માહિતીનો મધ્યસ્થ 58 ગુણ છે.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
( 1 ) જો અવલોકનો 6, 7, x, 8, y અને 14નો મધ્યક 9 હોય, તો x + y = ……..
( 2 ) પ્રથમ ñ પ્રાકૃતિક સંખ્યાઓનો મધ્યક ……. થાય.
( 3 ) જો અવલોકનો 64, 40, 48, x, 43, 48, 43 અને 34નો બહુલક 43 હોય, તો x + 3 = ………
( 4 ) ચડતા ક્રમે ગોઠવેલ અવલોકનો 24, 25, 26, x + 2, x + 3, 30, 31 અને 34નો મધ્યસ્થ 27.5 હોય, તો x = ……. .
( 5 ) જો નીચે આપેલ આવૃત્તિ-વિતરણનો મધ્યક 2.6 હોય, તો y = ……… .
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
( 1 ) ……… એ મધ્યવર્તી સ્થિતિમાનનું માપ નથી.
A. મધ્યક B. મધ્યસ્થ C. બહુલક D. વિસ્તાર
( 2 ) n અવલોકનોનો મધ્યક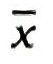 
છે. જો પ્રથમ અવલોકનમાં 1 ઉમેરીએ, બીજા અવલોકનમાં 2 ઉમેરીએ અને તે જ પ્રમાણે દરેક અવલોકનમાં ઉમેરો કરીએ, તો મળતાં નવાં અવલોકનોનો મધ્યક ……… થાય.
છે. જો પ્રથમ અવલોકનમાં 1 ઉમેરીએ, બીજા અવલોકનમાં 2 ઉમેરીએ અને તે જ પ્રમાણે દરેક અવલોકનમાં ઉમેરો કરીએ, તો મળતાં નવાં અવલોકનોનો મધ્યક ……… થાય.
( 3 ) સામાન્ય રીતે, કોઈ પણ આવૃત્તિ-વિતરણના મધ્યક, મધ્યસ્થ અને બહુલક વચ્ચેનો સંબંધ ……. છે.
A. બહુલક = 3 × મધ્યક – 2 × મધ્યસ્થ
B. બહુલક = 2 x×મધ્યસ્થ – 3 × મધ્યક
C. બહુલક = 3 × મધ્યસ્થ – 2 × મધ્યક
D. બહુલક = 3 × મધ્યસ્થ + 2 × મધ્યક
( 4 ) સામાન્ય રીતે, કોઈ પણ આવૃત્તિ-વિતરણ માટે બહુલક – મધ્યસ્થ = ……… × (મધ્યસ્થ – મધ્યક).
A. 1
B. 2
C. 3
D. 4
( 5 ) આપેલ આવૃત્તિ-વિતરણ માટે, ……… દોરીને તેનો મધ્યસ્થ શોધી શકાય છે.
A. સ્તંભાલેખ
B. આવૃત્તિવક્ર
C. આવૃત્તિ બહુકોણ
D. ઓજાઈવ
( 6 ) ચડતા ક્રમે ગોઠવેલ અવલોકનો 6, 7, x – 2, x, 17 અને 20નો મધ્યસ્થ 16 હોય, તો x = ……….
A. 15
B. 16
C. 17
D. 18
( 7 ) નીચે આપેલા આવૃત્તિ-વિતરણનો મધ્યસ્થ વર્ગ …….. છે.
A. 10 – 20
B. 20 – 30
C. 30 – 40
D. 40 – 50
(8) કોઈ આપેલ આવૃત્તિ-વિતરણ માટે, મધ્યસ્થ = 13.2 અને મધ્યક = 15.3. હોય, તો મધ્યક, મધ્યસ્થ અને બહુલકના આંતરસંબંધ મુજબ બહુલક = ……… થાય.
A. 8.5
B. 8.2
C. 8.8
D. 9
( 9 ) નીચે આપેલા આવૃત્તિ-વિતરણનો બહુલક વર્ગ ……… છે.
A. 0 – 20
B. 20 – 40
C. 40 – 60
D. 60 – 80
(10) જો કોઈ આવૃત્તિ-વિતરણનો બહુલક તેના મધ્યક કરતાં 12 વધુ હોય, તો બહુલક તેના મધ્યસ્થ કરતાં …….. વધુ હોય.
A. 4
B. 8
C. 6
D. 10
(11) બહુલક – મધ્યક = ……. (મધ્યસ્થ – મધ્યક)
A. 2
B. 4
C. 3
D. 6
3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ લખો :
( 1 ) જો અવલોકનો 16, 15, 17, 16, 15, x, 19, 17 અને 14નો બહુલક 15 હોય, તો x શોધો.
( 2 ) જો પ્રથમ n પ્રાકૃતિક સંખ્યાઓનો મધ્યક 5n/9 હોય, તો n શોધો.
( 3 ) નીચે આપેલ આવૃત્તિ-વિતરણના મધ્યસ્થ વર્ગની અધઃસીમા અને બહુલક વર્ગની ઊર્ધ્વસીમાનો સરવાળો શોધો :
( 4 ) કોઈ પણ માહિતી માટે તેના દરેક અવલોકનનો મધ્યકમાંથી લીધેલ વિચલનોનો સરવાળો કેટલો થાય?
( 5 ) નીચેના આવૃત્તિ-વિતરણમાં વર્ગ 40–50ની સંચયી આવૃત્તિ શોધો :
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here