Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 4 Quadratic Equations (દ્વિઘાત સમીકરણ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 4 Quadratic Equations (દ્વિઘાત સમીકરણ)
સ્વાધ્યાય – 4.1
1. નીચે આપેલ સમીકરણો દ્વિઘાત સમીકરણો છે કે કેમ તે ચકાસો :
(1) (x + 1)² = 2(x-3)
(2) x²-2x=(-2) (3-x)
(3)(x-2) (x + 1) = (x – 1) (x + 3)
(4) (x-3) (2x + 1) = x (x + 5)
(5) (2x-1) (x-3) = (x + 5) (x −1)
(6) x2+3x+1 = (x-2)²
(7) (x+2)3 = 2x (x² – 1)
(8) x3 – 4x2 – x + 1 = (x-2)³
( 1 ) અહીં, ડા.બા. = (x + 1)² = x² + 2x + 1 અને
જ. બા. = 2 (x – 3) = 2x – 6.
આથી (x + 1)² = 2(x – 3) ને
x2 + 2x + 1 = 2x – 6 તરીકે લખી શકાય.
∴ x² + 2x + 1 – 2x + 6 = 0
∴ x² + 7 = 0
આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું છે.
(a = 1, b = 0, c = 7)
આમ, આપેલ સમીકરણ દ્વિઘાત સમીકરણ છે.
( 2 ) અહીં, જ.બા, = (− 2) (3 − x) = – 6 + 2x.
આથી x2 – 2x = (– 2) (3 – x)ને
x2 – 2x = – 6 + 2x તરીકે લખી શકાય.
∴ x2 – 4x + 6 = 0
આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું છે.
(a = 1, b = – 4, c = 6)
આમ, આપેલ સમીકરણ દ્વિઘાત સમીકરણ છે.
( 3 ) અહીં, ડા.બા.= (x – 2) (x + 1) = x2 − x – 2 અને
જ.બા,= (x – 1) (x + 3) = x2 + 2x-3.
આથી (x – 2) (x + 1) = (x – 1) (x + 3)ને
x2 – x – 2 = x2 + 2x-3 તરીકે લખી શકાય.
∴ − 3x + 1 = 0
આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું નથી.
આમ, આપેલ સમીકરણ દ્વિઘાત સમીકરણ નથી.
( 4 ) અહીં, ડા.બા.= (x −3) (2x + 1) = 2x2 − 5x – 3 અને
જ.બા.= x (x + 5) = x2 + 5x.
આથી (x – 3) (2x + 1) = x (x + 5)ને
2x2 – 5x – 3 = x2 + 5x તરીકે લખી શકાય.
∴ x2 – 10x – 3 = 0
આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું છે.
(a = 1, b = – 10, c = – 3)
આમ, આપેલ સમીકરણ દ્વિઘાત સમીકરણ છે.
( 5 ) અહીં, ડા.બા. = (2x – 1) (x −3) = 2x2 − 7x + 3 અને
જ,બા,= (x + 5) (x – 1) = x2 + 4x – 5.
આથી આપેલ સમીકરણને
2x2 – 7x + 3 = x2 + 4x − 5 તરીકે લખી શકાય.
∴ x2 – 11x + 8 = 0
આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું છે.
(a = 1, b = − 11, c = 8)
આમ, આપેલ સમીકરણ દ્વિઘાત સમીકરણ છે.
( 6 ) અહીં‚ જ.બા. = (x – 2)2 = x2 – 4x + 4
આથી આપેલ સમીકરણને
x2 + 3x + 1 = x2 – 4x + 4 તરીકે લખી શકાય.
∴ 7x – 3 = 0
આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું નથી.
આમ, આપેલ સમીકરણ દ્વિઘાત સમીકરણ નથી.
( 7 ) અહીં, ડા.બા.= (x + 2)3 = x3 + 6x2 + 12x + 8 અને
જ.બા.= 2x (x2 − 1) = 2x3 – 2x.
આથી આપેલ સમીકરણને
x3 + 6x2 + 12x + 8 = 2x3 – 2x તરીકે લખી શકાય.
∴ – x3 + 6x2 + 14x + 8 = 0
આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું નથી.
આમ, આપેલ સમીકરણ દ્વિઘાત સમીકરણ નથી.
( 8 ) અહીં, જ.બા.= (x -2)3 = x3 – 6x2 + 12x – 8.
આથી આપેલ સમીકરણને
x3 – 4x2 – x + 1 = x3 – 6x2 + 12x – 8 તરીકે લખી શકાય.
∴ 2x2 – 13x + 9 = 0
આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું છે.
(a = 2, b = – 13, c = 9)
આમ, આપેલ સમીકરણ દ્વિઘાત સમીકરણ છે.
2. નીચે આપેલ પરિસ્થિતિઓને દ્વિઘાત સમીકરણ સ્વરૂપે દર્શાવો :
( 1 ) જમીનના એક લંબચોરસ ટુકડાનું ક્ષેત્રફળ 528 મી2 છે. તેની લંબાઈ (મીટરમાં), પહોળાઈ(મીટરમાં)ના બમણાથી એક મીટર જેટલી વધુ છે. આપણે જમીનના આ ટુકડાની લંબાઈ અને પહોળાઈ શોધવી છે.
ધારો કે, જમીનના લંબચોરસ ટુકડાની પહોળાઈ (મીટરમાં) x છે.
આથી તે ટુકડાની લંબાઈ (મીટરમાં) 2x + 1 થાય.
જમીનના લંબચોરસ ટુકડાનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
∴ 528 = (2x + 1) × x
(‘.’ ક્ષેત્રફળ 528 મી2 આપેલ છે.)
∴ 528 = 2x2 + x
∴ 2x2 + x – 528 = 0 એ આપેલ પરિસ્થિતિને દ્વિઘાત સમીકરણ સ્વરૂપે દર્શાવે છે. જેના ઉકેલ દ્વારા જમીનના ટુકડાની પહોળાઈ (x મી) અને લંબાઈ (2x + 1 મી) શોધી શકાય.
( 2 ) બે ક્રમિક ધન પૂર્ણાંકોનો ગુણાકાર 306 છે. આપણે આ પૂર્ણાંકો શોધવા છે.
ધારો કે, બે ક્રમિક ધન પૂર્ણાંકો x અને x + 1 છે.
આથી તેમનો ગુણાકાર = x (x+1) x2 + x થાય.
આ ગુણાકાર 306 આપેલ છે.
∴ x2 + x = 306
∴ x2 + x – 306 = 0 એ આપેલ પરિસ્થિતિને દ્વિઘાત સમીકરણ સ્વરૂપે દર્શાવે છે. જેના ઉકેલ દ્વારા ક્રમિક ધન પૂર્ણાંકો x અને x + 1 શોધી શકાય.
(૩) રોહનની માતા તેના કરતાં 26 વર્ષ મોટા છે. આજથી 3 વર્ષ પછી તેમની ઉંમર દર્શાવતી સંખ્યાઓનો ગુણાકાર (વર્ષમાં) 360 હશે. આપણે રોહનની હાલની ઉંમર શોધવી છે.
ધારો કે, રોહનની હાલની ઉંમર (વર્ષમાં) x છે.
આથી તેની માતાની હાલની ઉંમર (વર્ષમાં) x + 26 થાય.
3 વર્ષ પછી રોહનની ઉંમર (વર્ષમાં) x + 3 થશે
અને તેની માતાની ઉંમર (વર્ષમાં) x + 29 થશે.
તેઓની 3 વર્ષ પછીની ઉંમ૨નો (વર્ષમાંનો) ગુણાકાર 360 આપેલ છે.
આથી (x + 3) (x + 29) = 360
∴ x² + 32x + 87 – 360 = 0
∴ x2 + 32x – 273 = 0 એ આપેલ પરિસ્થિતિને દ્વિઘાત સમીકરણ સ્વરૂપે દર્શાવે છે. જેના ઉકેલ દ્વારા રોહનની તથા તેની માતાની હાલની ઉંમર (વર્ષમાં) અનુક્રમે x અને x + 26 શોધી શકાય.
( 4 ) એક ટ્રેન 480 કિમીનું અંતર અચળ ઝડપથી કાપે છે. જો ઝડપ 8 કિમી / કલાક ઓછી હોય, તો આટલું જ અંતર કાપવા તે ૩ કલાક વધુ લે છે, તો ટ્રેનની ઝડપ શોધો.
ધારો કે, ટ્રેનની સામાન્ય અચળ ઝડપ x કિમી/કલાક છે.
હવે, સમય = અંતર/ઝડપ

મહત્ત્વનાં અન્ય ઉદાહરણો
1. નીચે આપેલ સમીકરણો દ્વિઘાત સમીકરણો છે કે કેમ તે ચકાસો :

2. નીચે આપેલ પરિસ્થિતિઓને દ્વિઘાત સમીકરણ સ્વરૂપે દર્શાવોઃ



પાઠ્યપુસ્તકનાં ઉદાહરણો
3. સમીકરણ 2x2 – 5x + 3 = 0નાં બીજ અવયવ પાડીને શોધો.
આપણે સૌપ્રથમ મધ્યમ પદ –5xના બે ભાગ –2x અને – 2x કરીએ.

4. દ્વિઘાત સમીકરણ 6x2 – x – 2 = 0ના બીજ શોધો.
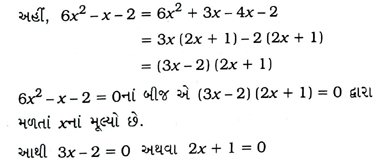

6. એક પ્રાર્થનાખંડનું ક્ષેત્રફળ 300 મી2 છે તથા તેની લંબાઈ તેની પહોળાઈના બમણાથી 1 મી વધારે છે. પ્રાર્થનાખંડની લંબાઈ તથા પહોળાઈ શોધો.
ધારો કે, પ્રાર્થનાખંડની પહોળાઈ x મી છે.
આથી તેની લંબાઈ (2x + 1) મી થાય અને
લંબચોરસ પ્રાર્થનાખંડનું ક્ષેત્રફળ = લંબાઈ × પહોળાઈ
= (2x + 1) x = (2x2 + x) મી2 થાય.
પરંતુ, પ્રાર્થનાખંડનું ક્ષેત્રફળ 300 મી2 આપેલ છે.
∴ 2x2 + x = 300
∴ 2x2 + x – 300 = 0 સમીકરણ મળે.
અવયવીકરણની રીત મુજબ,
2x2 – 24x + 25x – 300 = 0
∴ 2x (x – 12) + 25 (x – 12) = 0
∴ (x – 12) (2x + 25) = 0
આથી મેળવેલ સમીકરણના ઉકેલ x = 12 અથવા x = − 12.5 છે. પરંતુ, x એ પ્રાર્થનાખંડની પહોળાઈ હોવાથી ઋણ ન હોઈ શકે. આથી x = 12
આમ, પ્રાર્થનાખંડની પહોળાઈ = x = 12મી અને
પ્રાર્થનાખંડની લંબાઈ = 2x + 1 = 2(12) + 1 = 25 મી
સ્વાધ્યાય 4.2
1. નીચે આપેલ સમીકરણના ઉકેલ અવયવીકરણની રીતથી મેળવો :


2. પાઠ્યપુસ્તકનાં ઉદાહરણ (1)માં આપેલ પ્રશ્નોના ઉકેલ મેળવો :
( 1 ) જ્હૉન અને જીવંતી પાસે કુલ 45 લખોટીઓ હતી. પ્રત્યેક વ્યક્તિ પાંચ-પાંચ લખોટી ખોઈ કાઢે છે અને હવે તેમની પાસે બાકી રહેલી લખોટીઓની સંખ્યાનો ગુણાકાર 124 છે. તેમની પાસે શરૂઆતમાં કેટલી લખોટીઓ હતી?
( 2 ) એક કુટિર ઉદ્યોગ એક દિવસમાં કેટલાંક રમકડાં બનાવે છે. પ્રત્યેક રમકડું બનાવવાનો ખર્ચ (રૂપિયામાં) 55માંથી એક દિવસમાં ઉત્પાદિત થતાં રમકડાંની સંખ્યા બાદ કરીએ તેટલો છે. કોઈ એક ચોક્કસ દિવસે કુલ ઉત્પાદન ખર્ચ ₹ 750 છે. તે દિવસે ઉત્પાદિત રમકડાંની સંખ્યા શોધો.
( 1 ) ધારો કે, જ્હૉન પાસે x લખોટીઓ હતી.
આથી જીવંતી પાસેની લખોટીઓની સંખ્યા = 45 – x
જ્હૉન પાસે 5 લખોટીઓ ખોઈ કાઢ્યા બાદની લખોટીઓની સંખ્યા = x – 5.
જીવંતી પાસે 5 લખોટીઓ ખોઈ કાઢ્યા પછીની લખોટીઓની સંખ્યા = 45 – x – 5 = 40 – x.
આથી તેમનો ગુણાકાર = (x – 5) (40 − x)
= 40x – x2 – 200 + 5x
= x2 + 45x – 200
આ ગુણાકાર 124 આપેલ છે.
આથી – x2 + 45x – 200 = 124
∴ − x2 + 45x – 324 = 0
∴ x2 – 45x + 324 = 0
∴ x2 – 36x – 9x + 324 = 0
∴ x (x – 36) – 9 (x – 36) = 0
∴ (x – 36) (x – 9) = 0
∴ x – 36 = 0 અથવા x – 9 = 0
∴ x = 36 અથવા x = 9
અહીં, બંને જવાબ શક્ય છે.
∴ 45 − x = 45 – 36 = 9 અથવા
45 – x = 45 – 9 = 36.
આમ, જ્હૉન અને જીવંતી પાસે શરૂઆતમાં અનુક્રમે 36 અને 9 લખોટીઓ અથવા અનુક્રમે 9 અને 36 લખોટીઓ હતી.
( 2 ) ધારો કે, નિશ્ચિત દિવસે ઉત્પાદિત રમકડાંની સંખ્યા ૪ છે.
આથી પ્રત્યેક રમકડું બનાવવાનો ખર્ચ (રૂપિયામાં) = 55 – x.
આથી તે દિવસનો ૨મકડાં બનાવવાનો કુલ ખર્ચ (રૂપિયામાં) = x (55 − x).
આથી x (55 – x) = 750
∴ 55x – x2 = 750
∴ – x2 + 55x – 750 = 0
∴ x2 – 55x + 750 = 0
∴ x2 – 30x – 25x + 750 = 0
∴ x (x – 30) − 25 (x – 30) = 0
∴ (x – 30) (x – 25) = 0
∴ x – 30 = 0 અથવા x – 25 = 0
∴ x = 30 અથવા x = 25
અહીં, બંને જવાબ શક્ય છે.
આમ, તે દિવસે ઉત્પાદિત રમકડાંની સંખ્યા 30 અથવા 25 છે.
3. બે એવી સંખ્યાઓ શોધો કે જેમનો સરવાળો 27 અને ગુણાકાર 182 હોય.
જેમનો સરવાળો 27 થાય તેવી બે સંખ્યાઓ પૈકીની પહેલી સંખ્યા ધારો કે, x છે.
માટે, બીજી સંખ્યા 27 – x થાય અને તે બે સંખ્યાઓનો ગુણાકાર x (27–x) થાય.
હવે, આ ગુણાકાર 182 આપેલ છે.
∴ x (27 − x) = 182
∴ 27x – x2 – 182 = 0
∴ x2 – 27x + 182 = 0
∴ x2 – 14x – 13x + 182 = 0
∴ x (x – 14) − 13 (x – 14) = 0
∴ (x – 14) (x – 13) = 0
∴ x – 14 = 0 અથવા x − 13 = 0
∴ x = 14 અથવા x = 13
અહીં, બંને જવાબ શક્ય છે.
આથી જો x = 14, તો પહેલી સંખ્યા = x = 14 અને
બીજી સંખ્યા = 27 − x = 27 – 14 = 13 થાય.
જો x = 13, તો પહેલી સંખ્યા = x = 13 અને
બીજી સંખ્યા = 27 − x = 27 – 13 = 14 થાય.
આમ, દરેક સંજોગોમાં, માગેલ સંખ્યાઓ 13 અને 14 છે.
4. જેના વર્ગોનો સરવાળો 365 થાય એવી બે ક્રમિક ધન પૂર્ણાંક સંખ્યાઓ શોધો.
ધારો કે, બે ક્રમિક ધન પૂર્ણાંકો x અને x + 1 છે.
આથી તેમના વર્ગોનો સ૨વાળો
= (x)2 + (x + 1)2
= x2 + x2 + 2x + 1
= 2x2 + 2x + 1
આ સરવાળો 365 આપેલ છે.
∴ 2x2 + 2x + 1 = 365
∴ 2x2 + 2x – 364 = 0
∴ x2 + x – 182 = 0
∴ x2 + 14x – 13x – 182 = 0
∴ x (x + 14) − 13 (x + 14) = 0
∴ (x + 14) (x – 13) = 0
∴ x + 14 = ૦ અથવા x – 13 = 0
∴ x = − 14 અથવા x = 13
પરંતુ, x એ ધન પૂર્ણાંક હોવાથી x = – 14 શક્ય નથી,
આથી x = 13 અને x + 1 = 13 + 1 = 14
આમ, માગેલ ધન મિક પૂર્ણાંકી 13 અને 14 છે,
5. એક કાટકોણ ત્રિકોણનો વૈધ તેના પાયા કરતાં 7 સેમી નાનો છે. જ કર્ણની લંબાઈ 13 સેમી હોય, તો બાકીની બે બાજુનાં માપ શોધી.
ધારો કે, કાટકોણ ત્રિકોણનો પાયો x સૈમી છે.
આથી તેના વૈધની લંબાઈ (x – 7)સૈમી થાય.
કાટકોણ ત્રિકોણનો કર્ણ 13 સેમી છે,
પાયથાગોરસ પ્રમેય અનુસાર,
(પાયો)2 + (વેધ)2 = (કર્ણ)2
∴ (x)2 + (x – 7)2 = (13)2
∴ x2 + x2 – 14x + 49 = 169
∴ 2x2 – 14x – 120 = 0
∴ x2 – 7x – 60 = 0
∴ x2 – 12x + 5x – 60 = 0
∴ x (x – 12) + 5 (x – 12) = 0
∴ (x – 12) (x + 5) = 0
∴ x − 12 = 0 અથવા x + 5 = 0
∴ x = 12 અથવા x = – 5
ત્રિકોણના પાયાની લંબાઈ કદી ઋણ ન હોઇ શકે, આથી x = – 5 શક્ય નથી.
∴ x = 12
આથી ત્રિકોણનો પાયો = x = 12 સેમી અને
વેધ = x – 7 = 12 – 7 = 5 સેમી
આમ, આપેલ ત્રિકાની બાકીની બે બાજુના માપ 12 સેમી અને 5 સેમી છે,
6. એક કુટિર ઉદ્યોગ એક દિવસમાં કેટલીક બાટીની વસ્તુઓ બનાવે છે. એક નિશ્ચિત દિવસે એ જણાયું કે પ્રત્યેક વસ્તુની ઉત્પાદન કિંમત (રૂપિયામાં), તે વિર્સ ઉત્પાદિત વસ્તુના બમણા કરતાં 3 વધુ હતી, જો તે દિવસે કુલ ઉત્પાદન ખર્ચ ₹ 90 હોય, તો ઉત્પાદિત વસ્તુની સંખ્યા અને પ્રત્યેક વસ્તુની ઉત્પાદન કિંમત શોધો.
ધારો કે, તે નિશ્ચિત દિવસે ઉત્પાદિત થયેલ વસ્તુઓની સંખ્યા x છે.
માટે, આપેલ માહિતી મુજબ, દરેક વસ્તુની ઉત્પાદન કિંમત (રૂપિયામાં) 2x + 3 થાય,
આથી તે દિવસે કુલ ઉત્પાદન ખર્ચ (રૂપિયામાં)
= x (2x + 3) = 2x2 + 3x
આ કુલ ઉત્પાદન ખર્ચ ₹ 90 આપેલ છે,
∴ 2x2 + 3x = 90
∴ 2x2 + 3x – 90 = 0
∴ 2x² – 12x + 15x – 90 = 0
∴ 2x (x – 6) + 15 (x – 6) = 0
∴ (x – 6) (2x + 15) = 0
∴ x – 6 = 0 અથવા 2x + 15 = 0
∴ x = 6 અથવા x = – 15/2
x એ ઉત્પાદિત વસ્તુઓની સંખ્યા દર્શાવતી હોવાથી x = – 15/2 શક્ય નથી.
∴ x = 6 અને 2x + 3 = 2 (6) + 3 = 15
આમ, તે નિશ્ચિત દિવસે ઉત્પાદિત થયેલ વસ્તુઓની સંખ્યા 6 છે અને પ્રત્યેક વસ્તુની ઉત્પાદન કિંમત ₹ 15 છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. નીચે આપેલ સમીકરણના ઉકેલ અવયવીકરણની રીતથી મેળવો :
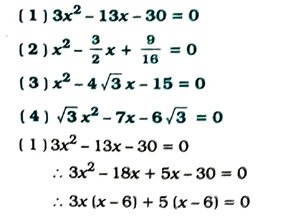


2. 30 ગુણની પરીક્ષામાં આર્યાએ મેળવેલ ગુણ કરતાં જો 10 માર્ક વધારે મેળવ્યા હોત, તો નવા ગુણના 9 ગણા એ તેણે મેળવેલ ગુણના વર્ગ જેટલા થાય. જો પરીક્ષામાં ઋણ ગુણાંકની પદ્ધતિ ન હોય, તો તેણે કેટલા ગુણ મેળવ્યા છે તે શોધો.
ધારો કે, આર્યાએ પરીક્ષામાં x ગુણ મેળવ્યા છે.
જો તેણે 10 ગુણ વધારે મેળવ્યા હોય, તો તેના ગુણ (x + 10) થાય અને તેના 9 ગણા 9 (x + 10) થાય. જે x2ની બરાબર છે.


પાઠ્યપુસ્તકનાં ઉદાહરણો
7. સમીકરણ 2x2 − 5x + 3 = 0ને પૂર્ણવર્ગની રીતે ઉકેલો.
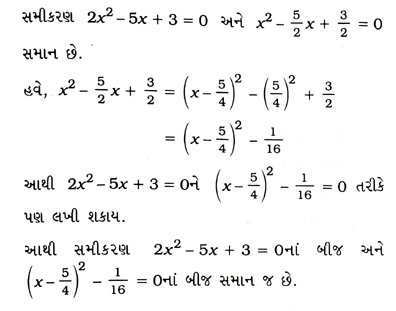
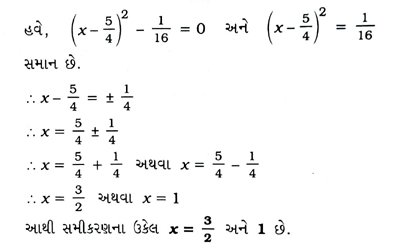
8. સમીકરણ 5x2 – 6x – 2 = 0નાં બીજ પૂર્ણવર્ગની રીતે શોધો.
સમીકરણની બંને બાજુ 5 વડે ગુણતાં,
25x2 – 30x – 10 = 0 મળે.
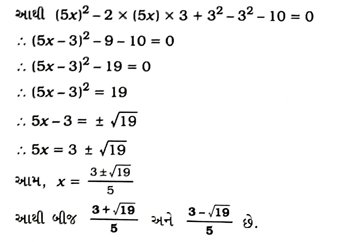
9. 4x2 + 3x + 5 = 0નાં બીજ પૂર્ણવર્ગની રીતે શોધો.
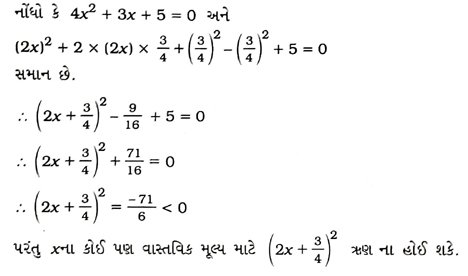
આથી કોઈ જ વાસ્તવિક સંખ્યા × આપેલ સમીકરણનું સમાધાન કરશે નહીં. આથી આપેલ સમીકરણનાં બીજ વાસ્તવિક હોય તે શક્ય નથી.
10. જમીનના એક લંબચોરસ ટુકડાનું ક્ષેત્રફળ 528 મી2 છે. તેની લંબાઈ (મીટરમાં), પહોળાઈ(મીટરમાં)ના બમણાથી એક મીટર જેટલી વધુ છે. દ્વિઘાત સૂત્રનો ઉપયોગ કરીને જમીનના ટુકડાની લંબાઈ તથા પહોળાઈ શોધો.
ધારો કે, જમીનના ટુકડાની પહોળાઈ x મીટર છે. આથી લંબાઈ (2x + 1) મીટર થાય. હવે, આપણને આપેલ છે કે જમીનના ટુકડાનું ક્ષેત્રફળ 528 મી2 છે. આથી x (2x + 1) = 528 અર્થાત્ 2x2 + x − 528 = 0.
a = 2, b = 1, c = – 528 માટે, આ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું છે.
આથી દ્વિઘાત સૂત્ર દ્વારા મળતો ઉકેલ,
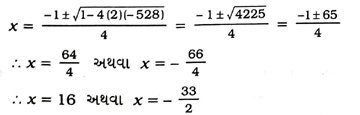
પરંતુ x ઋણ ના હોઈ શકે, કેમ કે તે એક પરિમાણ છે. આથી જમીનના લંબચોરસ ટુકડાની પહોળાઈ 16 મીટર અને લંબાઈ 33 મીટર થાય.
11. બે ક્રમિક અયુગ્મ ધન પૂર્ણાંક સંખ્યાઓના વર્ગોનો સરવાળો 290 હોય, તો બંને સંખ્યાઓ શોધો.
ધારો કે, બે ક્રમિક અયુગ્મ ધન પૂર્ણાંક સંખ્યાઓમાં નાની સંખ્યા x છે. આથી બીજી સંખ્યા x + 2 થાય.
આપેલ પ્રશ્ન મુજબ,
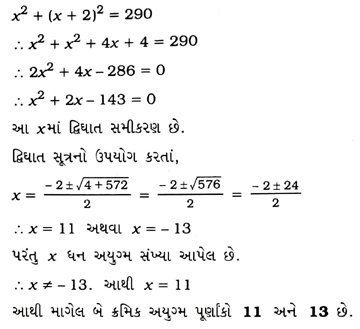
12. એક એવો લંબચોરસ બગીચો બનાવવો છે કે જેની પહોળાઈ તેની લંબાઈ કરતાં 3 મી ઓછી હોય અને તેનું ક્ષેત્રફળ જેનો પાયો લંબચોરસ બગીચાની પહોળાઈ જેટલો હોય અને વેધ 12 મી હોય તેવા પહેલેથી બનેલા સમઢિબાજુ ત્રિકોણાકાર બગીચાના ક્ષેત્રફળ કરતાં 4 મી2 વધુ હોય. લંબચોરસ બગીચાની લંબાઈ અને પહોળાઈ શોધો. (જુઓ આપેલ આકૃતિ)
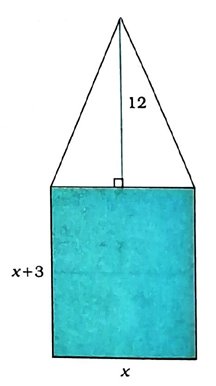

પરંતુ x એ બગીચાની પહોળાઈ દર્શાવે છે. આથી x ≠ − 1.
આથી x = 4
આમ, બગીચાની પહોળાઈ = 4 મી અને લંબાઈ = 7 મી થશે.
13. દ્વિઘાત સૂત્રનો ઉપયોગ કરી, શક્ય હોય તો, નીચેનાં દ્વિઘાત સમીકરણનાં બીજ મેળવો :

14. નીચેનાં સમીકરણનાં બીજ શોધો :
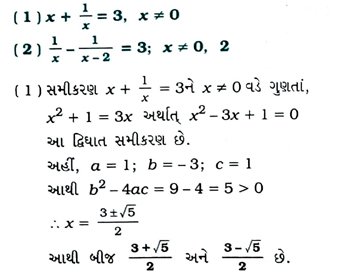

15. એક મોટર બોટની શાંત પાણીમાં ઝડપ 18 કિમી/કલાકની છે. જો 24 કિમી અંતર પ્રવાહની સામી દિશામાં કાપવા લાગતો સમય, પ્રવાહની દિશામાં તેટલું જ અંતર કાપવા લાગતાં સમય કરતાં 1 કલાક વધુ હોય, તો પ્રવાહની ઝડપ શોધો.

સ્વાધ્યાય – 4.3
1. નીચે આપેલ દ્વિઘાત સમીકરણનાં બીજ, શક્ય હોય તો, પૂર્ણવર્ગની રીતથી મેળવો :


પરંતુ કોઈ પણ વાસ્તવિક સંખ્યાનો વર્ગ ઋણ ન હોઈ શકે. આથી, આપેલ સમીકરણના વાસ્તવિક બીજનું અસ્તિત્વ નથી.
2. પ્રશ્ન 1માં આપેલ દ્વિઘાત સમીકરણનાં બીજ દ્વિઘાત સૂત્રનો ઉપયોગ કરી મેળવો.


3. નીચેનાં સમીકરણનાં બીજ શોધો :
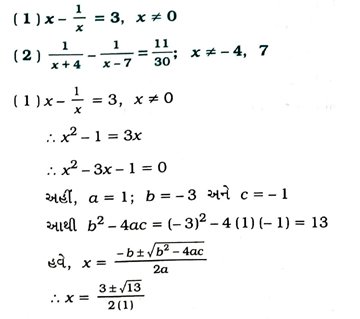
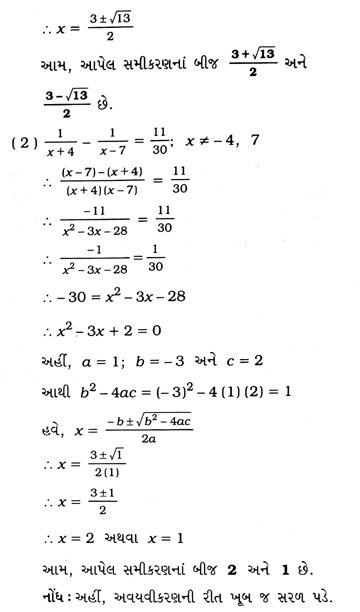
4. રહેમાનની આજથી ત્રણ વર્ષ પહેલાંની ઉંમર(વર્ષમાં)ના વ્યસ્ત અને હવે પછીના 5 વર્ષ પછીની ઉંમરના વ્યસ્તનો સરવાળો 1/3 છે. તેની અત્યારની ઉંમર શોધો.
ધારો કે, રહેમાનની અત્યારની ઉંમર x વર્ષ છે.
આથી આજથી ત્રણ વર્ષ પહેલાં તેની ઉંમર (x – 3) વર્ષ હતી અને આજથી પાંચ વર્ષ બાદ તેની ઉંમર (x + 5) વર્ષ થશે.
આ બે ઉંમર(વર્ષમાં)ના વ્યસ્તોનો સરવાળો 1/3 આપેલ છે.
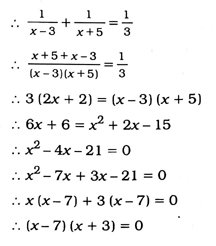
∴ x − 7 = 0 અથવા x + 3 = 0
∴ x = 7 અથવા x = − 3
હવે, x એ રહેમાનની અત્યારની ઉંમર દર્શાવે છે. આથી x ઋણ ન હોઈ શકે, એટલે કે x ≠ − 3.
∴ x = 7
આમ, રહેમાનની અત્યારની ઉંમર 7 વર્ષ છે.
5. એક વર્ગકસોટીમાં શેફાલીના ગણિત અને અંગ્રેજીના ગુણનો સરવાળો 30 છે. જો તેને ગણિતમાં 2 ગુણ વધુ અને અંગ્રેજીમાં 3 ગુણ ઓછા મળ્યા હોત, તો તેમનો ગુણાકાર 210 થયો હોત. તેણે આ બંને વિષયમાં મેળવેલ ગુણ શોધો.
ધારો કે, શેફાલીએ ગણિતમાં મેળવેલ ગુણ x છે.
આથી શેફાલીના અંગ્રેજીના ગુણ = 30 − x થાય, કારણ કે બે વિષયોમાં મેળવેલ કુલ ગુણ 30 છે.
જો તેને ગણિતમાં 2 ગુણ વધુ મળ્યા હોત, તો તેના ગણિતના ગુણ = (x + 2) થાય. તે જ રીતે, જો તેને અંગ્રેજીમાં 3 ગુણ ઓછા મળ્યા હોત, તો તેના અંગ્રેજીના ગુણ = 30 − x − 3 = 27 − x થાય.
∴ (x + 2) (27 − x) = 210
∴ 27x − x2 + 54 – 2x = 210
∴ − x + 25x + 54 – 210 = 0
∴ − x2 + 25x ― 156 = 0
∴ x2 – 25x + 156 = 0
∴ x2 – 13x – 12x + 156 = 0
∴ x (x – 13) – 12 (x – 13) = 0
∴ (x – 13) (x – 12) = 0
∴ x − 13 = 0 અથવા x − 12 = 0
∴ x = 13 અથવા x = 12
આથી 30 − x = 30 – 13 = 17 અથવા
30 − x = 30 − 12 = 18
આમ, શેફાલીએ ગણિત અને અંગ્રેજીમાં મેળવેલ ગુણ અનુક્રમે 13 અને 17 છે અથવા અનુક્રમે 12 અને 18 છે.
6. એક લંબચોરસ ખેતરના વિકર્ણનું માપ તેની નાની બાજુના માપથી 60 મીટર વધુ છે. જો મોટી બાજુ, નાની બાજુ કરતાં 30 મીટર વધુ હોય, તો ખેતરની બાજુઓનાં માપ શોધો.
ધારો કે, લંબચોરસ ખેતરની નાની બાજુનું માપ x મી છે.
આથી તે ખેતરના વિકર્ણનું માપ (x + 60) મી અને મોટી બાજુનું માપ (x + 30) મી થાય.
લંબચોરસના બધા જ ખૂણા કાટખૂણા હોય છે.
આથી પાયથાગોરસ પ્રમેય અનુસાર,
(નાની બાજુ)2 + (મોટી બાજુ)2 = (વિકર્ણ)2

આમ, લંબચોરસ ખેતરની નાની બાજુ (પહોળાઈ) 90 મી અને લાંબી બાજુ (લંબાઈ) 120 મી છે.
7. બે સંખ્યાઓના વર્ગોનો તફાવત 180 છે. નાની સંખ્યાનો વર્ગ મોટી સંખ્યા કરતાં 8 ગણો છે. બંને સંખ્યાઓ શોધો.


8. એક ટ્રેન એકધારી ઝડપે 360 કિમી અંતર કાપે છે. જો તેની ઝડપ 5 કિમી / કલાક વધુ હોય, તો આટલું જ અંતર કાપવા તેને 1 કલાક ઓછો સમય લાગે છે, તો ટ્રેનની ઝડપ શોધો.



10. એક ઝડપી ટ્રેન મૈસૂરુ અને બેંગલૂરુ વચ્ચેનું 132 કિમી અંતર કાપવા ધીમી ટ્રેન કરતાં 1 કલાક ઓછો સમય લે છે. (વચ્ચેના સ્ટેશનો પર ઊભા રહેવાનો સમય ધ્યાનમાં ના લો.) જો ઝડપી ટ્રેનની સરેરાશ ઝડપ, ધીમી ટ્રેનની સરેરાશ ઝડપ કરતાં 11 કિમી / કલાક વધુ હોય, તો બંને ગાડીની સરેરાશ ઝડપ શોધો.


11. બે ચોરસનાં ક્ષેત્રફળોનો સરવાળો 468 મી છે. જો તેમની પરિમિતિનો તફાવત 24 મી હોય, તો બંને ચોરસની બાજુઓની લંબાઈ શોધો.

મહત્ત્વનાં અન્ય ઉદાહરણો
1. નીચે આપેલ દ્વિઘાત સમીકરણનાં બીજ પૂર્ણવર્ગની રીતે શોધો :

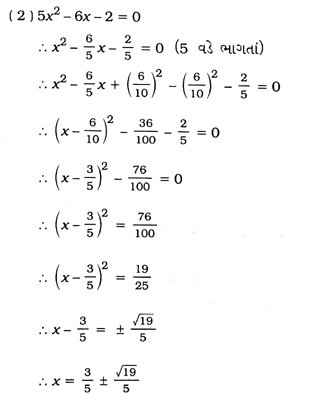

2. નીચે આપેલ દ્વિઘાત સમીકરણનાં બીજ દ્વિઘાત સૂત્રનો ઉપયોગ કરીને મેળવો :

3. નીચેનાં સમીકરણોનું સમાધાન કરતી ની કિંમતો શોધો : (કોઈ છેદ શૂન્ય નથી.)
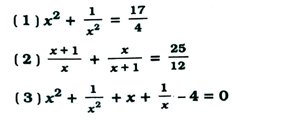


4. બે અંકની એક સંખ્યા તેના અંકોના સરવાળાથી ચાર ગણી અને અંકોના ગુણાકારથી ત્રણ ગણી છે, તે સંખ્યા શોધો.
ધારો કે, માગેલ સંખ્યાનો દશનો અંક x અને એકમનો અંક y છે.
આથી માગેલ સંખ્યા = 10x + y, સંખ્યાના અંકોનો સરવાળો = x + y અને સંખ્યાના અંકોનો ગુણાકાર = xy થાય.
આપેલ માહિતી મુજબ નીચેનાં બે સમીકરણ મળે :
10x + y = 4 (x + y) અને 10x + y = 3xy
10x + y = 4 (x + y)
∴ 10x + y – 4x + 4y
∴ 6x = 3y
∴ y = 2x
10x + y = 3xuમાં y = 2x મૂકતાં,
10x + 2x = 3 (x) (2x)
∴ 12x = 6x2
∴ 6x2 – 12x = 0
∴ 6x (x – 2) = 0
∴ x = 0 અથવા x − 2 = 0
∴ x = 0 અથવા x = 2
x = 0 માટે y = 0 અને માગેલ સંખ્યા = 0 મળે, જે શક્ય નથી.
∴ x = 2 અને y = 2x = 2 × 2 = 4
આથી માગેલ સંખ્યા = 10x + y = 10 (2) + 4 = 24 આમ, માગેલ સંખ્યા 24 છે.
5. ઝેબાની પાંચ વર્ષ પહેલાંની ઉંમર(વર્ષમાં)નો વર્ગ તેની હાલની ઉંમર (વર્ષમાં)ના પાંચ ગણા કરતાં 11 વધુ થાય છે. ઝેબાની હાલની ઉંમર શોધો.
ધારો કે, ઝેબાની હાલની ઉંમર x વર્ષ છે.
આથી પાંચ વર્ષ પહેલાંની ઝેબાની ઉંમર = (x – 5) વર્ષ આપેલ માહિતી મુજબ,
(x – 5)2 = 5x + 11
∴ x2 – 10x + 25 – 5x – 11 = 0
∴ x2 – 15x + 14 = 0
∴ (x – 14) (x – 1) = 0
∴ x − 14 = 0 અથવા x − 1 = 0
∴ x = 14 અથવા x = 1
પરંતુ, x એ ઝેબાની હાલની ઉંમર દર્શાવે છે. માટે, x = 1 લેવાથી ઝેબાની પાંચ વર્ષ પહેલાંની ઉંમર ઋણ થાય, જે શક્ય નથી.
∴ x = 14
આમ, ઝેબાની હાલની ઉંમર 14 વર્ષ છે.
પાઠ્યપુસ્તનાં ઉદાહરણો
16. દ્વિઘાત સમીકરણ 2x2 − 4x + 3 = 0નો વિવેચક શોધો અને તેના પરથી બીજનું સ્વરૂપ નક્કી કરો.
આપેલ દ્વિઘાત સમીકરણ a = 2, b = – 4, c = 3 માટે ax2 + bx + c = 0 પ્રકારનું છે. આથી વિવેચક
b2 – 4ac = (−4)2 − (4 × 2 × 3) = 16 − 24 = − 8 < 0 આથી આપેલ દ્વિઘાત સમીકરણને કોઈ વાસ્તવિક બીજ શક્ય નથી.
17. 13 મીટર વ્યાસવાળા એક વર્તુળાકાર બગીચાની સીમા પરના એક બિંદુએ એક થાંભલો એવી રીતે લગાવવો છે કે જેથી આ બગીચાના એક વ્યાસનાં બંને અંત્યબિંદુઓ A અને B આગળ બનેલ ફાટથી થાંભલાના અંતરનો તફાવત 7 મીટર હોય. શું આ શક્ય છે ? જો હા, તો બંને ફાટકથી કેટલે દૂર થાંભલો લગાવવો જોઈએ ?
પ્રથમ રેખાકૃતિ બનાવીએ. (જુઓ આપેલ આકૃતિ)
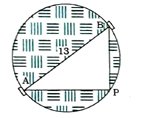
ધારો કે, P થાંભલાનું જરૂરી સ્થાન છે. ધારો કે થાંભલાથી ફાટક Bનું અંતર x મી, અર્થાત્ BP = x મી. હવે થાંભલાથી બંને ફાટકના અંતરનો તફાવત = AP – BP (અથવા BP – AP) = 7 મી.
આથી AP = (x + 7) મી
હવે, AB વ્યાસ હોવાથી AB = 13 મી
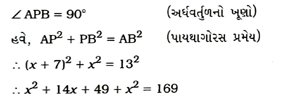
∴ 2x2 + 14x – 120 = 0
∴ 2x2 + 7x – 60 = 0
આથી થાંભલાનું ફાટક Bથી અંતર ‘x’ એ સમીકરણ
x2 + 7x – 60 = 0નું સમાધાન કરે છે.
આથી જો દ્વિઘાત સમીકરણનાં બીજ વાસ્તવિક હોય, તો થાંભલાનું સ્થાન નક્કી કરવું શક્ય બને. આ શક્ય છે કે કેમ, તે જોવા વિવેચકનો વિચાર કરીએ.
વિવેચક b2 – 4ac = 72 – 4 × 1 × (– 60) = 289 > 0
આથી આપેલ દ્વિઘાત સમીકરણનાં બે બીજ વાસ્તવિક બીજ છે અને આથી બગીચાની સીમા પર થાંભલો લગાવવાનું શક્ય છે.
દ્વિઘાત સમીકરણ x2 + 7x – 60 = 0ને દ્વિધાત સૂત્રથી ઉકેલતાં,

પરંતુ, x એ થાંભલા અને ફાટક B વચ્ચેનું અંતર હોવાથી, તે ધન જ હોવું જોઈએ. આથી x = − 12 ને અવગણવું જોઈએ. આથી, x = 5.
આથી સીમા પર થાંભલો એ રીતે લગાવવો જોઈએ કે જેથી તેનું ફાટક B થી અંતર 5 મી અને ફાટક A થી અંતર 12 મી હોય.
18. સમીકરણ 3x2 – 2x + 1/3 = 0નો વિવેચક શોધો. તે પરથી સમીકરણનાં બીજનું સ્વરૂપ નક્કી કરો. જો તે વાસ્તવિક હોય, તો મેળવો.
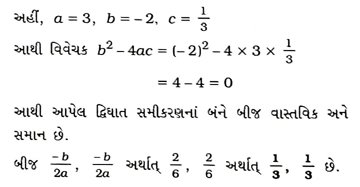
સ્વાધ્યાય – 4.4
1. નીચે આપેલાં દ્વિઘાત સમીકરણનાં બીજનાં સ્વરૂપ શોધો. જો તેમને વાસ્તવિક બીજ હોય, તો તે શોધો :
( 1 ) 2x2 – 3x + 5 = 0
( 2 ) 3x2 – 4√3 x + 4 = 0
( 3 ) 2x2 – 6x + 3 = 0
( 1 ) આપેલ સમીકરણ ax2 + bx + c = 0 સ્વરૂપનું છે,
જ્યાં a = 2; b = – 3 અને c = 5,
હવે, વિવેચક = b2 – 4ac
= (– 3)² – 4 (2) (5)
= 9 – 40 = – 31 < 0
આથી આપેલ સમીકરણને વાસ્તવિક બીજ નથી.

2. નીચેનાં દ્વિઘાત સમીકરણનાં બીજ સમાન હોય, તો kનું મૂલ્ય શોધો :

પરંતુ, k = 0 શક્ય નથી, કારણ કે k = 0 માટે સમીકરણ દ્વિઘાત સમીકરણ ૨હે નહીં, પરંતુ 6 = 0 મળે.
∴ k = 6
3. જેની લંબાઈ, પહોળાઈ કરતાં બમણી હોય અને ક્ષેત્રફળ 800 મી2 હોય એવી લંબચોરસ આંબાવાડી બનાવવી શક્ય છે? જો તમારો જવાબ ‘હા’ માં હોય, તો તેની લંબાઈ અને પહોળાઈ મેળવો.
માગ્યા મુજબની આંબાવાડી બનાવવી શક્ય છે તેમ માની લઈએ, તો ધારો કે તે આંબાવાડીની પહોળાઈ x મી છે.
આથી આંબાવાડીની લંબાઈ 2x મી થાય.
લંબચોરસ આંબાવાડીનું ક્ષેત્રફળ = લંબાઈ x પહોળાઈ
= 2x × x
= 2x2 મી2
માગ્યા મુજબ આંબાવાડીનું ક્ષેત્રફળ 800 મી2 છે.
∴ 2x² = 800
∴ 2x² – 800 = 0
∴ x2 – 400 = 0
જો ઉપરોક્ત સમીકરણને વાસ્તવિક બીજ હોય, તો આંબાવાડી બનાવવાનું શક્ય થાય.
અહીં, a = 1; b = 0 અને c = – 400
હવે, વિવેચક = b2 – 4ac
= (0)² – 4 (1) (– 400) = 1600 > 0
આમ, સમીકરણને વાસ્તવિક બીજ છે. આથી માગ્યા મુજબના માપવાળી આંબાવાડી બનાવવાનું શક્ય છે.
હવે, x2 – 400 = 0
∴ (x + 20) (x – 20) = 0
∴ x + 20 = 0 અથવા x – 20 = 0
∴ x = – 20 અથવા x = 20
પરંતુ, x એ આંબાવાડીની પહોળાઈ દર્શાવે છે. તેથી તે ઋણ ન હોઈ શકે, એટલે કે, x = – 20 શક્ય નથી.
∴ x = 20 અને 2x = 40
આમ, આંબાવાડીની લંબાઈ 40મી અને પહોળાઈ 20 મી રાખવી જોઈએ.
4. બે મિત્રોની ઉંમરનો સરવાળો 20 વર્ષ છે. 4 વર્ષ પહેલાં તેમની ઉંમર દર્શાવતી સંખ્યાઓનો ગુણાકાર (વર્ષમાં) 48 હતો. શું આ પરિસ્થિતિ શક્ય છે? જો હોય, તો તેમની અત્યારની ઉંમર શોધો.
ધારો કે, બે મિત્રોની અત્યારની ઉંમર x વર્ષ અને (20–x) વર્ષ છે.
આથી ચાર વર્ષ પહેલાં તેઓની ઉંમર (x – 4) વર્ષ અને (20 − x – 4) = (16–x) વર્ષ હતી.
આપેલ માહિતી મુજબ,
(x-4) (16-x) = 48
∴ 16x – x2 – 64 + 4x = 48
∴ – x² + 20x – 64 – 48 = 0
∴ – x² + 20x – 112 = 0
∴ x2 – 20x + 112 = 0
અહીં, a = 1; b = -20 અને c = 112
હવે, વિવેચક = b2 – 4ac
= (-20)²-4 (1) (112)
= 400-448 = -48 < 0
આથી સમીકરણને વાસ્તવિક બીજ નથી.
આમ, આપેલ પરિસ્થિતિ શક્ય નથી.
5. જેની પરિમિતિ 80 મી અને ક્ષેત્રફળ 400 મી2 હોય, તેવો લંબચોરસ બગીચો બનાવવાનું શક્ય છે? જો તે શક્ય હોય, તો તેની લંબાઈ અને પહોળાઈ શોધો.
ધારો કે, લંબચોરસ બગીચાની લંબાઈ x મી છે.
લંબચોરસ બગીચાની પરિમિતિ = 2 (લંબાઈ + પહોળાઈ)
∴ 80 = 2 (x + પહોળાઈ)
∴ 40 = x + પહોળાઈ
∴ પહોળાઈ = (40 – x) મી
હવે, લંબચોરસ બગીચાનું ક્ષેત્રફળ = લંબાઈ x પહોળાઈ
∴ 400 = x (40 – x)
∴ 400 = 40x – x2
∴ x2 – 40x + 400 = 0
અહીં, a = 1; b = – 40 અને c = 400.
હવે, વિવેચક = b2 – 4ac
= (-40)2 – 4 (1) (400)
= 1600 – 1600 = 0
આથી, સમીકરણનાં બીજ વાસ્તવિક છે. આથી આપેલ માપ મુજબનો લંબચોરસ બગીચો બનાવવાનું શક્ય છે.
x2 – 40x + 400 = 0
∴ x2 – 20x – 20x + 400 = 0
∴ x (x – 20) − 20 (x – 20) = 0
∴ (x – 20) (x – 20) = 0
∴ x – 20 = 0 અથવા x– 20 = 0
∴ x = 20 અથવા x = 20
આમ, માગ્યા મુજબના લંબચોરસ બગીચાની લંબાઈ = x = 20 મી અને પહોળાઈ = 40 – x = 40 – 20 = 20 મી
નોંધ : અહીં, માગેલ બગીચાનો આકાર ચોરસ બને છે, પરંતુ આપણે જાણીએ છીએ કે, દરેક ચોરસ એ લંબચોરસ છે જ.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. જો નીચેના દ્વિઘાત સમીકરણનાં બીજ વાસ્તવિક અને સમાન હોય, તો 1ત્ની કિંમત શોધો :

2. જો સમીકરણ
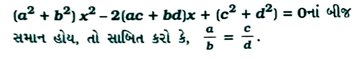

3. જેની પરિમિતિ 360 મી અને ક્ષેત્રફળ 8500 મી હોય તેવો લંબચોરસ પ્લૉટ શક્ય છે? જો હા, તો તેનાં માપ શોધો.


હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :

2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
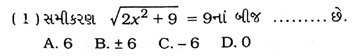


3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ આપો :

( 7 ) દ્વિઘાત સમીકરણ 6x2 – 13x + m = 0ના બંને બીજ પરસ્પર વ્યસ્ત હોય, તો mની કિંમત શોધો.
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) સમીકરણ x2 + x + 1 = 0ને વાસ્તવિક બીજ નથી.
( 2 ) દ્વિઘાત સમીકરણને ઓછામાં ઓછા બે વાસ્તવિક બીજ હોય.
( 3 ) સમીકરણ 25x2 – 5x – 11 = 0નો વિવેચક – 63 છે.
( 4 ) સમીકરણ x2 – 4x + 4 = 0નાં બીજ સમાન છે.
( 5 ) જો કોઈ દ્વિઘાત સમીકરણમાં x2ના સહગુણકની તથા અચળ પદની સંજ્ઞાઓ વિરોધી હોય, તો તે સમીકરણનાં બીજ વાસ્તવિક હોય.

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here