Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 6 Triangles (ત્રિકોણ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 6 Triangles (ત્રિકોણ)
સ્વાધ્યાય – 6.1
1. કૌંસમાં આપેલ શબ્દો પૈકી સાચા શબ્દનો ઉપયોગ કરીને ખાલી જગ્યા પૂરોઃ
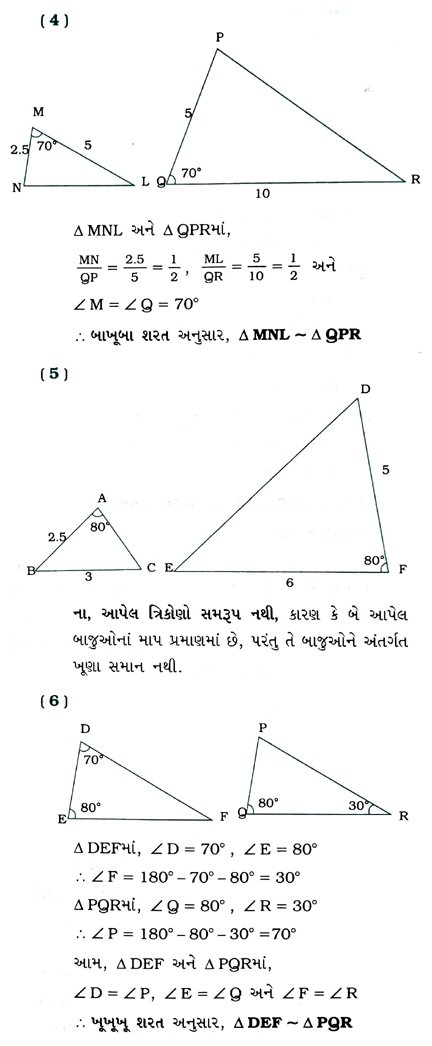
( 1 ) બધાં વર્તુળો ……. છે. (એકરૂપ, સમરૂપ)
( 2 ) બધા ચોરસો ……… છે. (સમરૂપ, એકરૂપ)
( 3 ) બધા ……….. ત્રિકોણો સમરૂપ છે. (સમઢિબાજુ, સમબાજુ)
( 4 ) જો (અ) બે બહુકોણના અનુરૂપ ખૂણાઓ ……. હોય. (બ) તેમની અનુરૂપ બાજુઓ ……. હોય, તો સમાન સંખ્યાની બાજુઓવાળા બે બહુકોણો સમરૂપ છે. (સમાન, સમપ્રમાણમાં)
જવાબ : ( 1 ) સમરૂપ ( 2 ) સમરૂપ ( 3 ) સમબાજુ ( 4 ) સમાન, સમપ્રમાણમાં
2. નીચેની જોડીઓનાં બે જુદાં જુદાં ઉદાહરણો આપો :
( 1 ) સમરૂપ આકૃતિઓ ( 2 ) સમરૂપ ન હોય તેવી આકૃતિઓ
( 1 ) સમરૂપ આકૃતિઓઃ કોઈ પણ બે ચોરસ હંમેશાં સમરૂપ છે. કોઈ પણ બે સમબાજુ ત્રિકોણ હંમેશાં સમરૂપ છે. કોઈ પણ બે વર્તુળ હંમેશાં સમરૂપ છે.
( 2 ) સમરૂપ ન હોય તેવી આકૃતિઓ ઃ કોઈ સમબાજુ ત્રિકોણ અને કોઈ ગુરુકોણ ત્રિકોણ સમરૂપ ન જ હોય. કોઈ સમબાજુ ત્રિકોણ અને કોઈ કાટકોણ ત્રિકોણ સમરૂપ ન જ હોય.
3. નીચેના ચતુષ્કોણો સમરૂપ છે કે નહીં તે જણાવો :
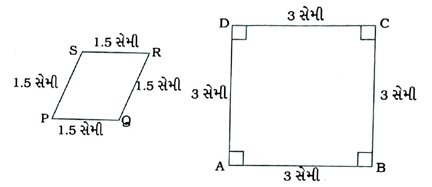
ના, કારણ કે તે ચતુષ્કોણોના શિરોબિંદુ વચ્ચેની કોઈ પણ સંગતતા માટે તેમની અનુરૂપ બાજુઓના ગુણોત્તર સમાન છે, પરંતુ અનુરૂપ ખૂણાઓ સમાન નથી.
પાઠ્યપુસ્તકનાં ઉદાહરણો
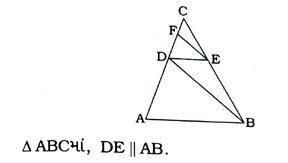
1. જો કોઈ એક રેખા Δ ABCની બાજુઓ AB અને ACને અનુક્રમે D અને Eમાં છેઠે છે તથા BCને સમાંતર છે, તો સાબિત કરો
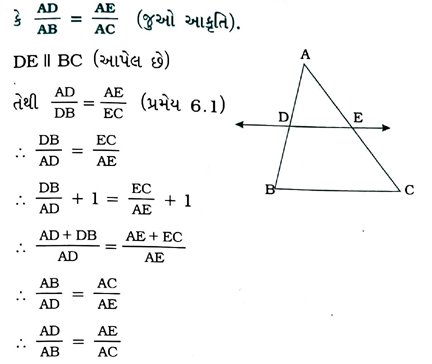


સ્વાધ્યાય – 6.2
1. આકૃતિ (1) અને (2)માં, DE || BC. (1)માં EC શોધો. (2)માં AD શોધો.


2. બિંદુઓ E અને F એ APORની બાજુઓ અનુક્રમે PQ અને PR પર આવેલાં છે. નીચેના દરેક વિકલ્પમાં EF || QR છે કે કેમ તે જણાવોઃ
( 1 ) PE = 3.9 સેમી, EQ = 3 સેમી, PF = 3.6 સેમી અને FR = 2.4 સેમી.
( 2 ) PE = 4 સેમી, QE = 4.5 સેમી, PF = 8 સેમી અને RF = 9 સેમી.
( 3 ) PQ = 1.28 સેમી, PR = 2.56 સેમી, PE = 0.18 સેમી અને PF = 0.36 સેમી.
બિંદુઓ E અને F Δ PQRની બાજુઓ અનુક્રમે PQ અને PR પર આવેલાં છે.

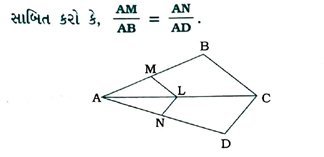
3. આપેલ આકૃતિમાં, જો LM || CB અને LN || CD હોય, તો


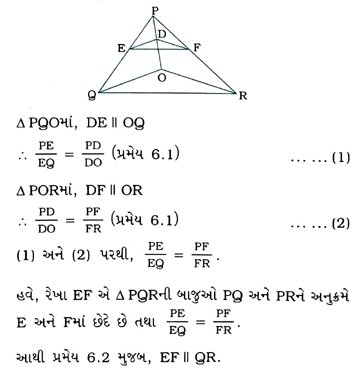
5. આપેલ આકૃતિમાં, DE || OQ અને DF || OR. સાબિત કરો કે, EF || QR.
6. આપેલ આકૃતિમાં, AB || PQ અને AC || PR બને તે રીતે બિંદુઓ A, B અને C અનુક્રમે OP, OQ અને OR પર આવેલાં છે, તો સાબિત કરો કે BC || QR.
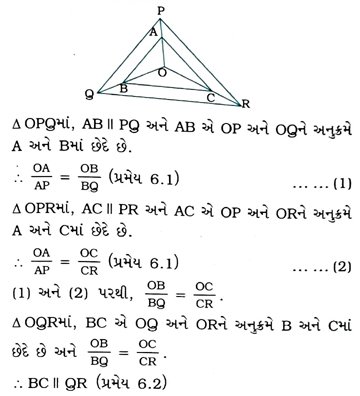
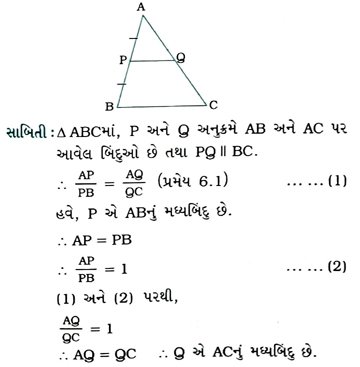
7. પ્રમેય 6.1નો ઉપયોગ કરીને, સાબિત કરો કે ત્રિકોણની એક બાજુના મધ્યબિંદુમાંથી પસાર થતી અને બીજી બાજુને સમાંતર રેખા, ત્રીજી બાજુને દુભાગે છે. (યાદ કરો, તમે ધોરણ IXમાં આ પરિણામ સાબિત કર્યું છે.)
પક્ષ : Δ ABCમાં, P એ બાજુ ABનું મધ્યબિંદુ છે. Pમાંથી દોરેલ BCને સમાંતર રેખા ACને ઊમાં છેદે છે.
સાધ્ય : Q એ ACનું મધ્યબિંદુ છે. :
નોંધ : ધોરણ IXમાં આ જ પરિણામ સમાંતરબાજુ ચતુષ્કોણના ગુણધર્મોની મદદથી સાબિત કરેલ હતું.
8. પ્રમેય 6.2નો ઉપયોગ કરીને, સાબિત કરો કે ત્રિકોણની બે બાજુઓનાં મધ્યબિંદુઓમાંથી પસાર થતી રેખા ત્રિકોણની ત્રીજી બાજુને સમાંતર હોય છે. (યાદ કરો, તમે ધોરણ IXમાં આ પરિણામ સાબિત કર્યું છે.)




મહત્ત્વનાં અન્ય ઉદાહણો
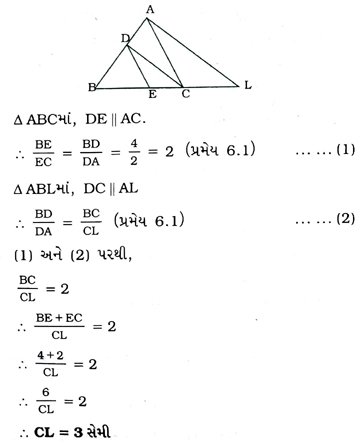
1. આપેલ આકૃતિમાં, CD || LA અને DE || AC. જો BE = 4 સેમી અને EC = 2 સેમી હોય, તો CLની લંબાઈ શોધો.
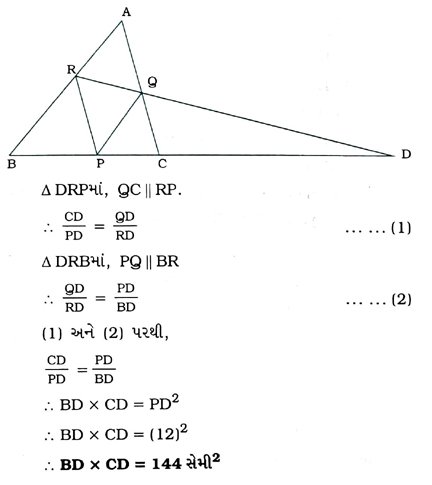
2. આપેલ આકૃતિમાં, PQ || BA અને PR || CA. જો PD = 12 સેમી હોય, તો BD × CD શોધો.
3. આપેલ આકૃતિમાં, AB || DE અને BD || EF. સાબિત કરો કે, DC2 = CF × AC.

પાઠ્યપુસ્તકનાં ઉદાહરણો
4. આપેલ આકૃતિમાં, જો PQ || RS, તો સાબિત કરો કે Δ POQ ∼ Δ SOR.

5. આપેલ આકૃતિનું નિરીક્ષણ કરો અને ∠P શોધો.


6. આપેલ આકૃતિમાં, OA · OB = OC · OD, તો સાબિત કરો કે ∠A = ∠C અને ∠B = ∠D.

7. 90 સેમી ઊંચાઈવાળી એક છોકરી વીજળીના થાંભલાના તળિયેથી 1.2 મી / સેની ઝડપથી દૂર જઈ રહી છે. જો વીજળીનો ગોળો જમીનના સમતલથી 3.6 મીટર ઊંચે હોય, તો ચાર સેકન્ડ પછી તેના પડછાયાની લંબાઈ શોધો.
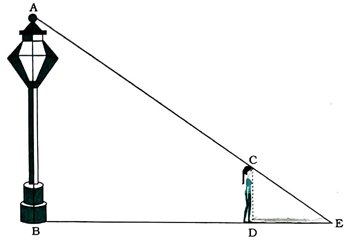
ધારો કે, AB એ વીજળીનો થાંભલો છે અને CD વીજળીના થાંભલાથી 4 સેકન્ડ ચાલ્યા પછીની પરિસ્થિતિમાં છોકરીનું સ્થાન દર્શાવે છે. (જુઓ આપેલ આકૃતિ)
આકૃતિ પરથી જોઈ શકાય કે, DE છોકરીનો પડછાયો છે. ધારો કે, DE એ x મીટર છે.

8. આપેલ આકૃતિમાં, CM અને RN અનુક્રમે Δ ABC અને Δ PQRની મધ્યગાઓ છે. જો Δ ABC ~ Δ PQR હોય, તો સાબિત કરો કે

સ્વાધ્યાય – 6.3
1. આપેલ આકૃતિમાં આપેલ ત્રિકોણો પૈકી કઈ જોડીના ત્રિકોણો સમરૂપ છે, તે જણાવો. પ્રશ્નનો જવાબ આપવા કઈ સમરૂપતાની શરતનો ઉપયોગ કર્યો તે લખો અને સમરૂપ ત્રિકોણની જોડીઓને સંકેતમાં લખો :



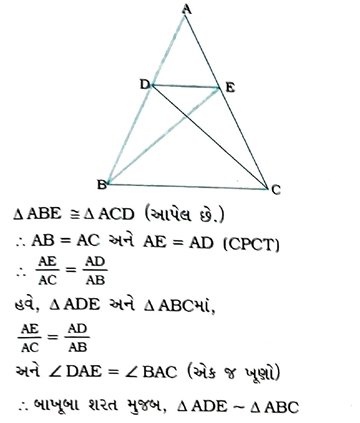
6. આપેલ આકૃતિમાં, જો Δ ABE = Δ ACD હોય, તો સાબિત કરો કે Δ ADE ~ Δ ABC.
7. આપેલ આકૃતિમાં, Δ ABCના વેધ AD અને CE એક્બીજાને P બિંદુમાં છેદે છે. સાબિત કરો કે,
( 1 ) Δ AEP ~ Δ CDP
( 2 ) Δ ABD ~ Δ CBE
( 3 ) Δ AEP ~ Δ ADB
( 4 ) Δ PDC ~ Δ BEC

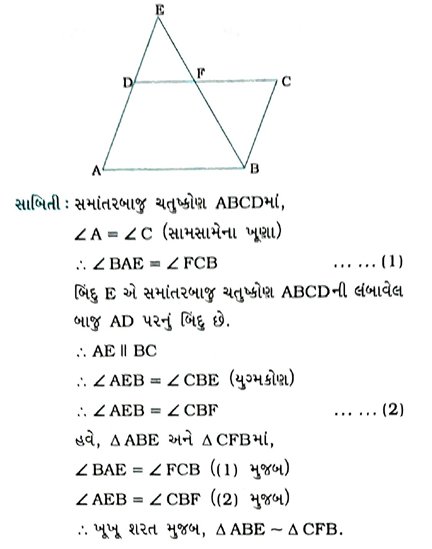
8. બિંદુ E એ સમાંતરબાજ઼ ચતુોણ ABCDની લંબાવેલ બાજુ AD પરનું બિંદુ છે. BE એ CDને Fમાં છેઠે છે, સાબિત કરો કે, Δ ABE ~ Δ CFB,
પક્ષ : બિંદુ E એ સમાંતરબાજુ ચતુષ્કોણ ABCD ની લંબાવેલ બાજુ AD પરનું બિંદુ છે. BE એ CDને માં છેદે છે.
સાધ્ધ : Δ ABE ~ Δ CFB
9. આપેલ આકૃતિમાં, ત્રિકોણ ABC અને AMP કાટકોણ ત્રિકોણ છે અને તેમાં ખૂણા B અને M કાટખૂણા છે. સાબિત કરો કે,

10. D અને મેં એ Δ ABC અને Δ EFGની બાજુઓ અનુક્રમે AB અને FE પર આવેલા હોય તેવી રીતે CD અને GH અનુક્રમે ∠ACB અને ∠EGF ના દ્વિભાજક છે. જો Δ ABC ~ Δ FEG હોય, તો સાબિત કરો કે

11. આપેલ આકૃતિમાં, E એ સમદ્વિબાજુ ત્રિકોણ ABCની લંબાવેલ બાજુ CB પર આવેલ બિંદુ છે તથા AB = AC. જો AD ⊥ BC અને EF ⊥ AC હોય, તો સાબિત કરો કે Δ ABD ~ Δ ECF.

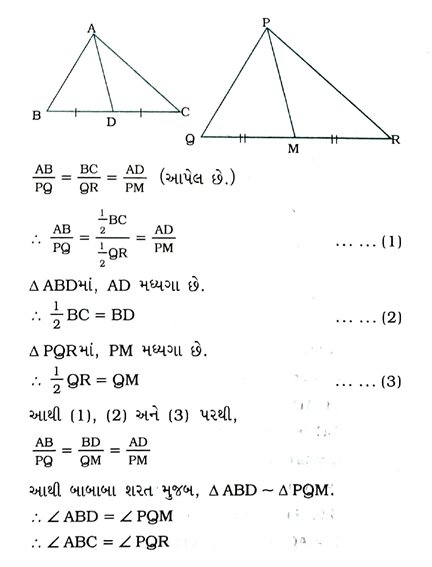
12. Δ ABC ની બાજુઓ AB અને BC તથા મધ્યગા AD અનુક્રમે Δ PQRની બાજુઓ PQ અને QR તથા મધ્યગા PMને સમપ્રમાણમાં છે (જુઓ આપેલ આકૃતિ). સાબિત કરો કે Δ ABC ∼ Δ PQR.

13. બિંદુ D એ Δ ABC ની બાજુ BC પરનું એવું બિંદુ છે કે ∠ADC = ∠BAC. સાબિત કરો કે, CA2 = CB · CD.

14. Δ ABCની બાજુઓ AB અને AC તથા મધ્યગા AD એ અનુક્રમે Δ PQRની બાજુઓ PQ અને PR તથા મધ્યગા PMને સમપ્રમાણમાં છે. સાબિત કરો કે, Δ ABC ~ Δ PQR.

15. એક 6 મીટર ઊંચા શિરોલંબ વાંસનો જમીન પર પડતો પડછાયો 4 મીટર લાંબો છે. એ જ વખતે એક મિનારાનો પડછાયો 28 મીટર લાંબો છે. મિનારાની ઊંચાઈ શોધો.

અહીં, AB એ શોલંબ વાંસ છે તથા BC તેનો પડછાયો છે. તે જ રીતે, PQ મિનારો છે અને QR તેનો પડછાયો છે.
બંને પડછાયાની લંબાઈ એક જ સમયે માપવામાં આવતી હોવાથી ∠C અને ∠R બંને સૂર્યનો ઉત્સેધકોણ દર્શાવે છે.

16. જો Δ ABC ∼ Δ PQR તથા AD અને PM અનુક્રમે Δ ABC અને A PQR ની મધ્યગા હોય, તો સાબિત કરો કે


મહત્ત્વનાં અન્ય ઉદાહરણો
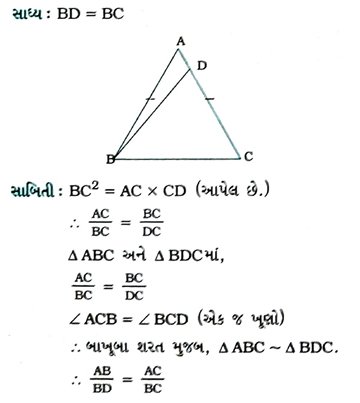
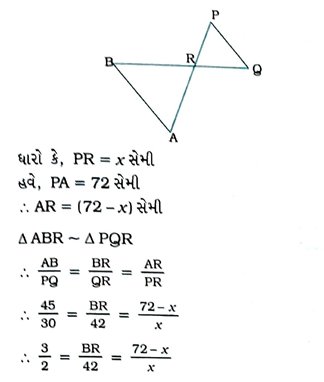
1. સમઢિભુજ Δ ABCમાં AB = AC અને AC પર બિંદુ D એવું છે કે જેથી BC2 = AC × CD થાય. સાબિત કરી કે, BD = BC.
પક્ષ : સમઢિભુજ Δ ABCમાં AB = AC અને AC પર બિંદુ D એવું છે કે જેથી BC2 = AC × CD થાય,
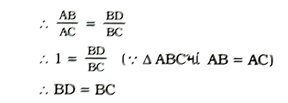
2. આપેલ આકૃતિ પરથી xની કિંમત a, b અને ના સ્વરૂપમાં શોધો.
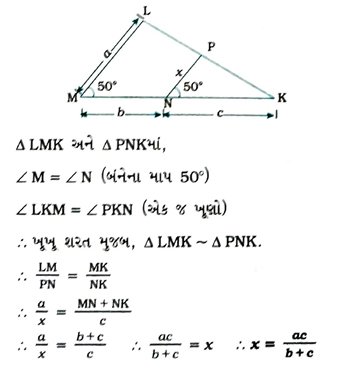
3. આપેલ આકૃતિમાં, Δ ABR ~ Δ PQR. જો PQ = 30 સેમી, AB = 45 સેમી, AP = 72 સેમી અને QR = 42 સેમી હોય, તો PR, AR અને BR શોધો.

પાઠ્યપુસ્તકનાં ઉદાહરણો
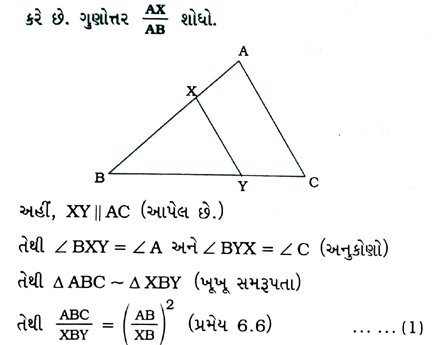
9. આપેલ આકૃતિમાં, રેખાખંડ XY એ Δ ABCની બાજુ ACને સમાંતર છે અને તે ત્રિકોણનું સમાન ક્ષેત્રફળના ભાગોમાં વિભાજન

સ્વાધ્યાય – 6.4
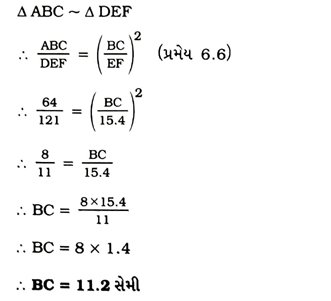
1. Δ ABC ~ Δ DEF છે. તેમનાં ક્ષેત્રફળો અનુક્રમે 64 સેમી2 અને 121 સેમી2 છે. જો EF = 15.4 સેમી હોય, તો BC શોધો.
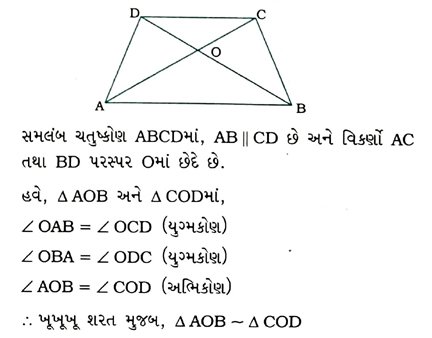
2. સમલંબ ચતુષ્કોણ ABCDમાં AB || CD છે. તેના વિકર્ણો એકબીજાને બિંદુ Oમાં છેદે છે. જો AB = 2CD હોય, તો Δ AOB અને Δ CODનાં ક્ષેત્રફળોનો ગુણોત્તર શોધો.
3. આપેલ આકૃતિમાં, ABC અને DBC એક જ પાયા BC પરના બે ત્રિકોણો છે. જો AD એ BCને Oમાં છેદે, તો સાબિત

4. જો બે સમરૂપ ત્રિકોણોનાં ક્ષેત્રફળો સમાન હોય, તો સાબિત કરો કે તે એકરૂપ છે.


5. D, E અને F અનુક્રમે Δ ABCની બાજુઓ AB, BC અને CAનાં મધ્યબિંદુઓ છે. Δ DEF અને Δ ABCનાં ક્ષેત્રફળોનો ગુણોત્તર શોધો.

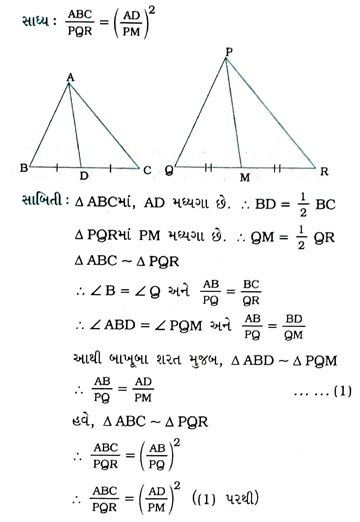
6. સાબિત કરો કે, બે સમરૂપ ત્રિકોણોનાં ક્ષેત્રફળોનો ગુણોત્તર તેમની અનુરૂપ મધ્યગાના ગુણોત્તરના વર્ગ બરાબર હોય છે,
પક્ષ : Δ ABC ~ Δ PQR. AD અને PM અનુક્રમે Δ ABC અને Δ PQRની મધ્યગાઓ છે.
7. સાબિત કરો કે, ચોરસની કોઈ એક બાજુ પર દોરેલા સમબાજુ ત્રિકોણનું ક્ષેત્રફળ, તે ચોરસના વિકર્ણ પર દોરેલા સમબાજુ ત્રિકોણના ક્ષેત્રફળથી અડધું હોય છે.
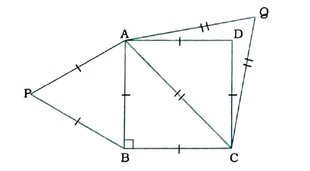
ABCD ચોરસ છે. Δ PAB એ ચોરસની બાજુ AB પર ઘેરેલ સમબાજુ ત્રિકોણ છે તથા Δ QAC એ ચોરસના વિકર્ણ AC પર દોરેલ સમબાજુ ત્રિકોણ છે.
Δ ABCમાં, ∠B = 90° અને AB = BC (ચોરસના ગુણધર્મો)
હવે, AC2 = AB2 + BC2 (પાયથાગોરસ પ્રમેય)
∴ AC2 = AB2 + AB2
∴ AC2 = 2AB2

8. જેમાં D એ BCનું મધ્યબિંદુ છે, એવા બે સમબાજુ ત્રિકોણો ABC અને BDE છે. ત્રિકોણો ABC અને BDEનાં ક્ષેત્રફળોનો ગુણોત્તર ……… થાય.

9. બે સમરૂપ ત્રિકોણોની બાજુઓનો ગુણોત્તર 4 : 9 છે. આ ત્રિકોણોનાં ક્ષેત્રફળોનો ગુણોત્તર ……. થાય.
(A) 2 : 3 (B) 4 : 9 (C) 81 : 16 (D) 16 : 81
સાચો વિકલ્પ (D) 16: 81 છે.
પ્રમેય 6.6 મુજબ,
બે સમરૂપ ત્રિકોણોનાં ક્ષેત્રફળોનો ગુણોત્તર
= (તેમની અનુરૂપ બાજુઓનો ગુણોત્તર)2
= (4:9)2
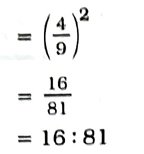
મહત્ત્વનાં અન્ય ઉદાહરણો
1. આપેલ આકૃતિમાં, DE || BC છે. જો DE : BC = 3 : 5

2. બે સમરૂપ ત્રિકોણોનાં ક્ષેત્રફળ અનુક્રમે 121 સેમી2 અને 64 સેમી2 છે. જો પહેલાં ત્રિકોણની મધ્યગાની લંબાઈ 12.1 સેમી હોય, તો બીજા ત્રિકોણની અનુરૂપ મધ્યગાની લંબાઈ શોધો.

3. Δ ABCમાં, ∠B = 90°, BM ⊥ AC, BC = 5 સેમી અને AC = 12 સેમી. Δ BMC અને Δ ABCનાં ક્ષેત્રફળોનો ગુણોત્તર શોધો.

પાઠ્યપુસ્તકનાં ઉદાહરણો
10. આપેલ આકૃતિમાં, ∠ACB = 90° અને CD ⊥ AB. સાબિત

11. એક નિસરણી દીવાલને અઢેલીને એવી રીતે ગોઠવી છે કે જેથી તેનો નીચેનો છેડો દીવાલથી 2.5 મીટર દૂર રહે અને તેનો ઉપરનો છેડો જમીનથી 6 મીટર ઊંચે એક બારીને અડકે. નિસરણીની લંબાઈ શોધો.
ધારો કે, AB નિસરણી છે અને CA દીવાલ છે તથા A બારી છે (જુઓ આકૃતિ).

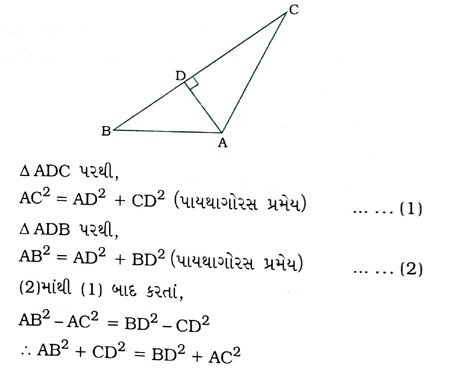
12. આપેલ આકૃતિમાં, જો AD ⊥ BC, તો સાબિત કરો કે AB2 + CD2 = BD2 + AC2.
13. ખૂણો A કાટખૂણો હોય તેવા ત્રિકોણ ABCમાં BL અને CM મધ્યગાઓ છે. સાબિત કરો કે, 4 (BL2 + CM2) = 5BC2.

14. O એ લંબચોરસ ABCDના અંદરના ભાગનું કોઈ બિંદુ હોય (જુઓ આકૃતિ), તો સાબિત કરો કે OB2 + OD2 = OA2 + OC2.

સ્વાધ્યાય – 6.5
1. નીચે ત્રિકોણની બાજુઓ આપેલી છે. તે પૈકી કયા ત્રિકોણો કાટકોણ ત્રિકોણો છે, તે નક્કી કરો. જે ત્રિકોણ કાટકોણ ત્રિકોણ હોય, તેના કર્ણની લંબાઈ શોધો :
( 1 ) 7 સેમી, 24 સેમી, 25 સેમી
( 2 ) 3 સેમી, 8 સેમી, 6 સેમી
( 3 ) 50 સેમી, 80 સેમી, 100 સેમી
( 4 ) 13 સેમી, 12 સેમી, 5 સેમી
( 1 ) 7 સેમી, 24 સેમી, 25 સેમી
અહીં, સૌથી મોટી બાજુ 25 સેમી છે.
252= 625 અને 72 + 242 = 49 + 576 = 625
∴ 252 = 72 + 242
અહીં, સૌથી મોટી બાજુની લંબાઈનો વર્ગ બાકીની બે બાજુઓના વર્ગના સરવાળા જેટલો છે. આથી 7 સેમી, 24 સેમી અને 25 સેમી બાજુઓવાળો ત્રિકોણ કાટકોણ ત્રિકોણ છે અને તેના કર્ણની લંબાઈ 25 સેમી છે.
( 2 ) 3 સેમી, 8 સેમી, 6 સેમી
અહીં, સૌથી મોટી બાજુ 8 સેમી છે.
82 = 64 અને 32 + 62 = 9 + 36 = 45
∴ 82 ≠ 32 + 62
આથી 3 સેમી, 8 સેમી અને 6 સેમી બાજુઓવાળો ત્રિકોણ કાટકોણ ત્રિકોણ નથી.
( 3 ) 50 સેમી, 80 સેમી, 100 સેમી
અહીં, સૌથી મોટી બાજુ 100 સેમી છે.
1002 = 10000 અને
502 + 802 = 2500 + 6400 = 8900
∴ 1002 ≠ 502 +802
આથી 50 સેમી, 80 સેમી અને 100 સેમી બાજુઓવાળો ત્રિકોણ કાટકોણ ત્રિકોણ નથી.
( 4 ) 13 સેમી, 12 સેમી, 5 સેમી
અહીં, સૌથી મોટી બાજુ 13 સેમી છે.
132 = 169 અને 12² + 5² = 144 + 25 = 169
∴ 13² = 122 +52
અહીં, સૌથી મોટી બાજુની લંબાઈનો વર્ગ બાકીની બે બાજુઓના વર્ગના સરવાળા જેટલો છે. આથી 13 સેમી, 12 સેમી અને 5 સેમી બાજુઓવાળો ત્રિકોણ કાટકોણ ત્રિકોણ છે અને તેના કર્ણની લંબાઈ 18 સેમી છે.
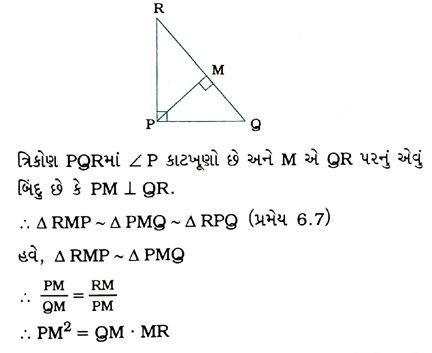
2. ત્રિકોણ PQRમાં ∠P કાટખૂણો છે અને M એ QR પરનું એવું બિંદુ છે કે PM ⊥ QR. સાબિત કરો કે, PM2 = QM · MR.
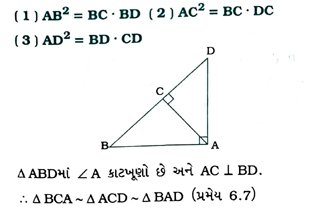
3. આપેલ આકૃતિમાં, ત્રિકોણ ABDમાં ∠A કાટખૂણો છે અને AC ⊥ BD. સાબિત કરો કે,

4. સમઢિબાજુ કાટકોણ ત્રિકોણ ABCમાં ∠C કાટખૂણો છે. સાબિત કરો કે, AB2 = 2AC2.
ABC એ સમદ્વિબાજુ કાટકોણ ત્રિકોણ છે, જેમાં ∠C કાટખૂણો છે.
આથી Δ ABCમાં AB કર્ણ છે અને બાકીની બે બાજુઓ સમાન છે, એટલે કે, BC = AC.

5. સમઢિબાજુ ત્રિકોણ ABCમાં AC = BC. જો AB2 = 2AC2 હોય, તો સાબિત કરો કે ABC કાટકોણ ત્રિકોણ છે.
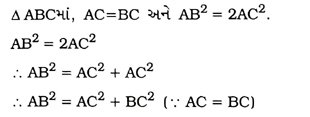
આથી પાયથાગોરસ પ્રમેયના પ્રતીપ મુજબ, Δ ABC કાટકોણ ત્રિકોણ છે, જેમાં ∠C કાટખૂણો છે.
6. સમબાજુ ત્રિકોણ ABCની બાજુ 2a છે. તેના દરેક વેધ શોધો.
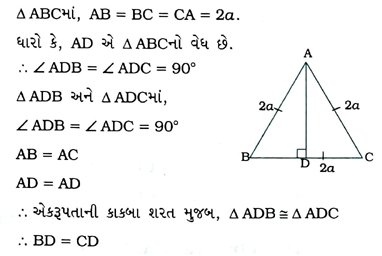

7. સાબિત કરો કે, સમબાજુ ચતુષ્કોણની બાજુઓના વર્ગોનો સરવાળો તેના વિકર્ણોના વર્ગોના સરવાળા જેટલો થાય છે.

8. આપેલ આકૃતિમાં, ૦ ત્રિકોણ ABCની અંદરનું બિંદુ છે, OD ⊥ BC, OE ⊥ AC અને OF ⊥ AB. સાબિત કરો કે,
( 1 ) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
( 2 ) AF2 + BD2 + CE2 = AE2 + CD2 + BF2

9. 10 મીટર લાંબી એક નિસરણી જમીનથી 8 મીટર ઊંચે આવેલી એક બારીને અડકે છે. નિસરણીના નીચેના છેડાનું દીવાલના તળિયેથી અંતર શોધો.
અહીં, AB દીવાલ છે તથા A બારી છે અને AC નિસરણી છે.
આથી AC = 10મી અને AB = 8 મી.
Δ ABCમાં, ∠B = 90°.
∴ AC2 = AB2 + BC2 (પાયથાગોરસ પ્રમેય)
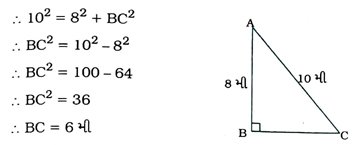
આમ, નિસરણીના નીચેના છેડાનું દીવાલના તળિયેથી અંતર 6મી છે.
10. 18 મીટર ઊંચા શિરોલંબ થાંભલાના ઉપરના છેડાથી 24 મીટર લાંબા તારનો એક છેડો જોડાયેલો છે. તે તારનો બીજો છેડો ખીલા સાથે જોડાયેલો છે. થાંભલાના આધારથી કેટલા અંતરે ખીલો લગાડવામાં આવે, તો તાર તંગ રહે?

11. એક વિમાન એક વિમાનમથકની ઉત્તર દિશામાં 1000 કિમી / કલાકની ઝડપથી ઊડે છે. એ જ સમયે, 1 બીજું એક વિમાન એ જ વિમાનમથકની પશ્ચિમ દિશામાં 1200 કિમી / કલાકની ઝડપે ઊડે છે. 1½ કલાક પછી આ વિમાનો એકબીજાથી કેટલા દૂર હશે?
અહીં, A વિમાનમથક છે. B એ 1000 કિમી / કલાકની ઝડપે ઉત્તર દિશામાં ઊડતા પ્રથમ વિમાનનું 1½ પછીનું સ્થાન તથા C એ 1200 કિમી / કલાકની ઝડપે પશ્ચિમ દિશામાં ઊડતા દ્વિતીય વિમાનનું 1½ કલાક પછીનું સ્થાન છે.
[નોંધ : પ્રશ્નમાં વિમાનોની ઊંચાઈનો ઉલ્લેખ કરેલ નથી. તેથી સરળતા માટે આપણે B અને C સરખી ઊંચાઈ પર લઈશું. તેમજ વિમાનમથક દર્શાવતા બિંદુ Aને પણ તે જ ઊંચાઈ ૫૨ સમજીશું.]

12. 6 મીટર અને 11 મીટર ઊંચાઈના બે થાંભલા સમતલ જમીન પર આવેલા છે. જો થાંભલાના નીચેના છેડા વચ્ચેનું અંતર 12 મીટર હોય, તો તેમના ઉપરના છેડા વચ્ચેનું અંતર શોધો.

અહીં, AB અને CD એ અનુક્રમે 6 મી અને 11 મી ઊંચાઈ ધરાવતા બે થાંભલા છે. જેમના નીચેના છેડા વચ્ચેનું અંતર 12 મી છે.
આથી AB = 6 મી, BD = 12 મી, CD = 11 મી, ∠B = 90° અને ∠D = 90°.
AE || BD દોરો.
હવે, ચતુષ્કોણ ABDEમાં,
∠B = ∠D = ∠E = ∠A = 90°
માટે, ABDE લંબચોરસ છે.
∴ ED = AB = 6 મી અને AE = BD = 12 મી

13. Δ ABCમાં ∠C કાટખૂણો છે અને D અને E અનુક્રમે તેની બાજુઓ CA અને CB પરનાં બિંદુઓ છે. સાબિત કરો કે,
AE² + BD² = AB² + DE².
Δ ABCમાં, ∠C કાટખૂણો છે અને D અને E અનુક્રમે બાજુઓ CA અને CB પરનાં બિંદુઓ છે.

આથી ચારેય ત્રિકોણો BCD, BCA, ECD અને ECA કાટકોણ ત્રિકોણ થાય જે દરેકમાં ∠C કાટખૂણો છે.
આથી દરેક ત્રિકોણમાં પાયથાગોરસ પ્રમેયનો ઉપયોગ થઈ શકે.

14. Aમાંથી Δ ABCની બાજુ BC પર દોરેલો લંબ BCને Dમાં એવી રીતે છેદે છે કે DB = 3CD (જુઓ આપેલ આકૃતિ).
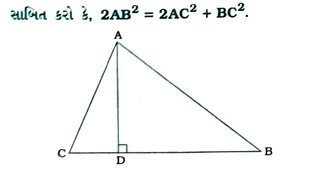


16. સમબાજુ ત્રિકોણમાં સાબિત કરો કે, કોઈ પણ બાજુના વર્ગના 3 ગણા એ તેના કોઈ પણ વેધના વર્ગના 4 ગણા બરાબર છે.

17. સાચો જવાબ જણાવો અને ચકાસો :

મહત્ત્વનાં અન્ય ઉદાહરણો
1. ચતુષ્કોણ ABCDમાં ∠B = 90° અને
AD2 = AB2 + BC2 + CD2. સાબિત કરો કે, ∠ACD = 90°


2. Δ ABC માં, ∠C = 90° અને P અને Q બિંદુઓ અનુક્રમે CA અને CB પર આવેલાં એવાં બિંદુઓ છે કે જેથી CP: PA = CQ : QB = 2 : 1 થાય. સાબિત કરો કે, 9 (AQ² + BP²) = 13 AB².

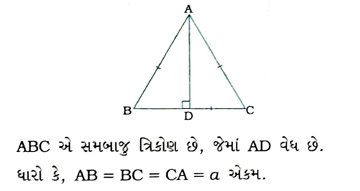
3. ΔABCમાં, AD, BE અને CF મધ્યગાઓ છે. સાબિત કરો કે, 4 (AD² + BE² + CF²) = 3 (AB² + BC² + AC²).
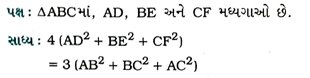

સ્વાધ્યાય – 6.6
- આ સ્વાધ્યાય પરીક્ષા માટે ધ્યાનમાં લેવાનો નથી.
1. આપેલ આકૃતિમાં, PS એ ΔPQRના ∠QPRનો દ્વિભાજક છે.

રચના: Qમાંથી PSને સમાંતર રેખા દોરો, જે લંબાવેલ RPને Mમાં છેદે છે.
સાબિતી : Δ MQRમાં બિંદુઓ P અને S અનુક્રમે MR અને QRનાં બિંદુઓ છે તથા PS|| MQ.

2. આપેલ આકૃતિમાં, ΔABCમાં BD ⊥ AC, DM ⊥ BC અને DN ⊥ AB થાય તેવું બિંદુ D કર્ણ AC પર છે. સાબિત કરો કે,
(1) DM² = DN · MC
(2) DN2 = DM · AN

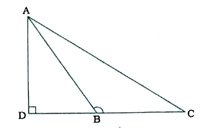
3. આપેલ આકૃતિમાં, Δ ABCમાં, ∠ABC > 90° અને AD ⊥ લંબાવેલ CB. સાબિત કરો કે,
AC² = AB² + BC² + 2BC · BD.

4. આપેલ આકૃતિમાં, Δ ABC માં, ∠ABC < 90° અને AD ⊥ BC છે. સાબિત કરો કે,
AC² = AB² + BC² – 2BC · BD.

5. આપેલ આકૃતિમાં, AD એ Δ ABCની મધ્યગા છે અને AM ⊥ BC. સાબિત કરો કે,
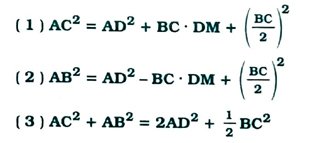

6. સાબિત કરો કે, સમાંતરબાજુ ચતુષ્કોણના વિકર્ણોના વર્ગોનો સરવાળો તેની બાજુઓના વર્ગોના સરવાળા જેટલો હોય છે.
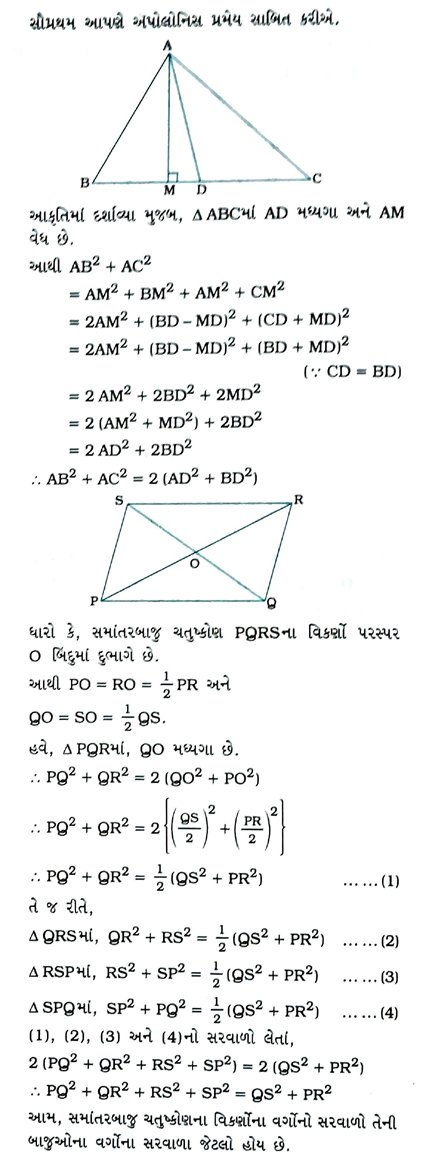
7. આપેલ આકૃતિમાં, બે જીવાઓ AB અને CD એકબીજાને બિંદુ Pમાં છેદે છે. સાબિત કરો કે,
( 1 ) Δ APC ~ Δ DPB
( 2 ) AP · PB = CP · DP

8. આપેલ આકૃતિમાં, એક વર્તુળની બે જીવાઓ AB અને CD (લંબાવીએ તો) વર્તુળના બહારના ભાગમાં એકબીજાને Pમાં છેદે છે. સાબિત કરો કે,
( 1 ) Δ PAC ~ Δ PDB
( 2 ) PA • PB = PC • PD



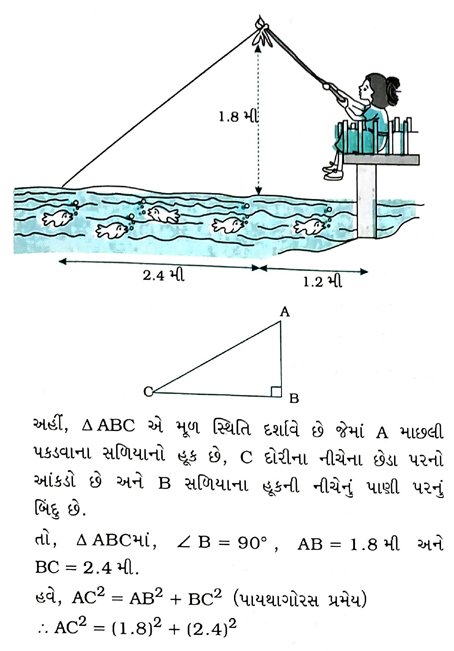
10. નાઝીમા પાણીના પ્રવાહમાં માછલીઓ પકડી રહી છે. તેનો માછલી પકડવાનો સળિયાનો હૂંક પાણીની સપાટીથી 1.8 મીટર ઊંચે છે અને દોરીના નીચેના છેડા પરનો આંકડો પાણીની સપાટી પર એવી રીતે સ્થિર છે કે નાઝીમાથી તેનું અંતર 3.6 મીટર છે અને સળિયાના હૂક નીચેની પાણીની સપાટીથી તેનું અંતર 2.4 મીટર છે. એવું માની લઈએ કે (સળિયાના હૂકથી આંકડા સુધી) તેની દોરી તંગ છે, તો તેણે કેટલી દોરી બહાર કાઢી છે? (જુઓ આપેલ આકૃતિ) જો તે દોરીને 5 સેમી / સેના દરથી અંદર ખેંચે, તો 12 સેકન્ડ પછી નાઝીમાનું આંકડાથી સમક્ષિતિજ અંતર કેટલું હશે?

હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
( 1 ) Δ ABC ~ Δ DEF અને 2AB = DE. જો BC = 8 સેમી હોય, તો EF = …….. સેમી.
( 2 ) Δ ABCમાં, ∠Aનો દ્વિભાજક BCને Dમાં છેદે છે. જો AB = 6 સેમી, AC = 5 સેમી અને BD = 3 સેમી હોય, તો BC = …… સેમી.
(૩) બે સમરૂપ ત્રિકોણો ABC અને DEFના ક્ષેત્રફળ અનુક્રમે 144 સેમી2 અને 81 સેમી2 છે. જો Δ ABCની સૌથી મોટી બાજુનું માપ 36 સેમી હોય, તો Δ DEFની સૌથી મોટી બાજુનું માપ સેમી હોય.
( 4 ) Δ ABCમાં, બિંદુ P અને Q અનુક્રમે AB અને ACનાં બિંદુઓ છે તથા PQ || BC. જો AP = 5 સેમી, PB = 12 સેમી અને AQ = 8 સેમી હોય, તો AC = …….. સેમી.
( 5 ) Δ ABCમાં, ∠B = 90° . જો AC = 73 સેમી અને BC = 55 સેમી હોય, તો AB = ……. સેમી.
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
( 1 ) એક વ્યક્તિ સ્થળ Aથી 24 મી પશ્ચિમ દિશામાં B સ્થળે જાય છે અને ત્યાંથી 7મી ઉત્તર દિશામાં C સ્થળે જાય છે. સ્થળ A અને C વચ્ચેનું સીધું અંતર …… મી થાય.
A. 31
B. 17
C. 25
D. 26
( 2 ) આપેલ આકૃતિમાં, Δ ABCનો ખૂણો B કાટખૂણો છે તથા BD વેધ છે, તો Δ ADB ~ Δ …… .
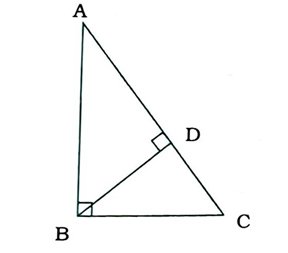
A. BAC
B. BCA
C. BCD
D. BDC


3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ આપો :
( 1 ) 12 મી ઊંચા એક શિરોલંબ થાંભલાના પડછાયાની લંબાઈ 8મી છે. તે જ સમયે, એક ટાવરના પડછાયાની લંબાઈ 40 મી છે. ટાવરની ઊંચાઈ શોધો.
( 2 ) એક ચોરસના વિકર્ણની લંબાઈ 7√2 સેમી છે. ચોરસનું ક્ષેત્રફળ શોધો.
( 3 ) a સેમી બાજુ ધરાવતા સમબાજુ ત્રિકોણનું ક્ષેત્રફળ કેટલું થાય?
( 4 ) Δ ABCમાં, AB = 11 સેમી, BC = 60 સેમી અને CA = 61 સેમી હોય, તો Δ ABCનો પ્રકાર જણાવો.
( 5 ) Δ ABCમાં, AD મધ્યગા છે. જો AB = 6 સેમી, AC = 8 સેમી અને AD = 5 સેમી હોય, તો BC શોધો.
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :

5. વ્યાખ્યા આપો :
( 1 ) સમરૂપ બહુકોણો
( 2 ) સમરૂપ ત્રિકોણો
( 3 ) સમકોણિક ત્રિકોણો
6. નીચેનાં વિધાનો લખો :
( 1 ) સમપ્રમાણતાનું મૂળભૂત પ્રમેય
( 2 ) થેલ્સના પ્રમેયનું પ્રતીપ
( 3 ) સમરૂપતાની ખૂખૂખૂ શરત
( 4 ) સમરૂપતાની ખૂજ્જૂ શરત
( 5 ) સમરૂપતાની બાબાબા શરત
( 6 ) સમરૂપતાની બાખૂબા શરત
( 7 ) સમરૂપતાની કાકબા શરત
( 8 ) પાયથાગોરસ પ્રમેય
( 9 ) પાયથાગોરસ પ્રમેયનું પ્રતીપ

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here