Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 7 Coordinate Geometry (યામ ભૂમિતિ)
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 7 Coordinate Geometry (યામ ભૂમિતિ)
સ્વાધ્યાય – 7.1
1. નીચે આપેલ બિંદુઓની જોડ વચ્ચેનું અંતર શોધો :
2. બિંદુઓ (0, 0) અને (36, 15) વચ્ચેનું અંતર શોધો. હવે તમે વિભાગ 7.2માં ચર્ચા કરેલ તે બે શહેરો A અને B વચ્ચેનું અંતર શોધી શકો.
આમ, આપેલ બિંદુઓ વચ્ચેનું અંતર 39 છે.
હા, હવે આપણે પાઠ્યપુસ્તકના વિભાગ 7.2માં ચર્ચા કરેલ બે શહેરો A અને B વચ્ચેનું અંતર શોધી શકીશું.
શહેર B શહેર Aથી 36 કિમી પૂર્વમાં અને 15 કિમી ઉત્તરમાં આવેલ છે. આથી જો આપણે શહેર A ઉગમબિંદુ પર આવેલ છે તેમ ધારીએ, તો શહેર Aના યામ (0, 0) થાય અને તેથી શહેર Bના યામ (36, 15) થાય. હવે, ઉપર ગણતરી કરી તે મુજબ બિંદુઓ A (0, 0) અને B (36, 15) વચ્ચેનું અંતર 39 છે. આથી શહેર A અને શહેર B વચ્ચેનું અંતર 39 કિમી થાય.
3. બિંદુઓ (1, 5), (2, 3) અને (– 2, – 11) સમરેખ છે કે નહીં તે નક્કી કરો.
ધારો કે, આપેલ બિંદુઓ A (1, 5), B (2, 3) અને C (– 2, − 11) છે.
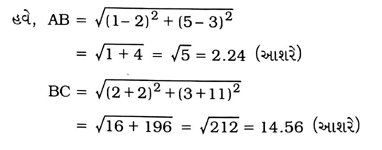
4. ચકાસો કે (5, −2), (6, 4) અને (7, – 2) એ સમદ્વિબાજુ ત્રિકોણનાં શિરોબિંદુઓ છે.
5. એક વર્ગખંડમાં ચાર મિત્રો આપેલ આકૃતિમાં દર્શાવેલ બિંદુઓ, A, B, C અને D દ્વારા દર્શાવેલ સ્થાન પર બેઠા છે. ચંપા અને ચમેલી વર્ગમાં આવી અને થોડી મિનિટોના અવલોકન બાદ ચંપાએ ચમેલીને પૂછ્યું કે “શું તું એવું માને છે કે ABCD ચોરસ છે?’ ચમેલી અસહમત થાય છે. અંતરસૂત્રનો ઉપયોગ કરી કોણ સાચું છે તે શોધો.
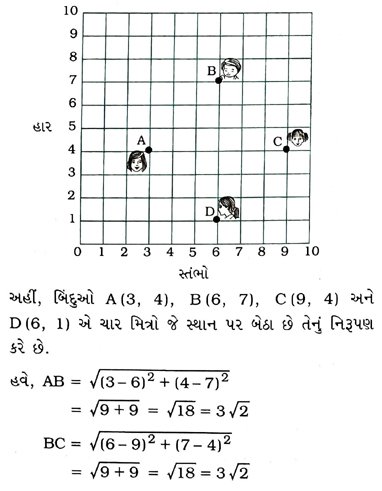
6. નીચે દર્શાવેલાં બિંદુઓથી જો ચતુષ્કોણ રચાતો હોય, તો તેનો પ્રકાર જણાવો અને તમારા જવાબ માટે કારણ આપો :
7. જે (2, − 5) અને (–2, 9)થી સમાન અંતરે હોય તેવું ૪-અક્ષ પરનું બિંદુ શોધો.
x-અક્ષ પરનાં કોઈ પણ બિંદુના યામ (x, 0) સ્વરૂપના હોય. ધારો કે, P (x, 0) એ માગેલ બિંદુ છે જે આપેલ બિંદુઓ A (2, – 5) અને B (–2, 9)થી સમાન અંતરે છે. આથી PA = PB.
8. બિંદુઓ P (2, – 3) અને Q (10, y) વચ્ચેનું અંતર 10 એકમ હોય તો yની કિંમત શોધો.
બિંદુઓ P (2, − 3) અને Q(10, y) વચ્ચેનું અંતર 10 આપેલ છે.
9. જો Q (0, 1) એ P (5, −3) અને R (x, 6)થી સમાન અંતરે હોય, તો ની કિંમત શોધો. અંતર QR અને PR પણ શોધો.
Q(0, 1) એ P (5, – 3) અને R (x, 6)થી સમાન અંતરે છે.
10. બિંદુ (x, y) એ બિંદુઓ (3, 6) અને (−3, 4)થી સમાન અંતરે હોય, તો x અને y વચ્ચેનો સંબંધ મેળવો.
અહીં, બિંદુ P (x, y) એ બિંદુઓ A (3, 6) અને B (– 3, 4)થી સમાન અંતરે છે.
∴ PA = PB
∴ PA² = PB²
મહત્ત્વનાં અન્ય ઉદાહરણો
1. દર્શાવો કે, બિંદુઓ P (a, b + c), Q (b, c + a) અને R (c, a + b) સમરેખ બિંદુઓ છે.
2. દર્શાવો કે, A (3, 10), B (6, 5), C (1, 2) અને D (– 2, 7) એ ચોરસનાં શિરોબિંદુઓ છે.
3. આપેલ ત્રણ બિંદુઓ A (5, 1), B (– 3, 7) અને C (7, − 1)થી સમાન અંતરે હોય તેવાં બિંદુનાં યામ શોધો.
અથવા
Δ ABCનાં શિરોબિંદુઓ A (5, 1), B(-3, −7) અને C (7, – 1) હોય, તો તેનું પરિકેન્દ્ર શોધો.
પાઠ્યપુસ્તકનાં ઉદાહરણો
6. બિંદુઓ (4, – ૩) અને (8, 5)ને જોડતા રેખાખંડનું 3: 1 ગુણોત્તરમાં અંતઃવિભાજન કરતા બિંદુના યામ શોધો.
ધારો કે, P (x, y) એ માગેલ બિંદુ છે.
વિભાજન સૂત્રનો ઉપયોગ કરતાં,
7. બિંદુ (– 4, 8) એ બિંદુઓ A (– 6, 10) અને B (3, – 8)ને જોડતા રેખાખંડનું કયા ગુણોત્તરમાં વિભાજન કરે?
ધારો કે, (– 4, 6) એ ABનું m1 : m2 ગુણોત્તરમાં અંતઃવિભાજન કરે છે.
વિભાજન સૂત્રનો ઉપયોગ કરતાં,
∴ 7k = 2
∴ k : 1 = 2 : 7
y-યામની ચકાસણી કરી લેવી.
આથી બિંદુ – 4, 6) એ બિંદુઓ A (– 6, 10) અને B (3, – 8)ને જોડતા રેખાખંડનું 2:7 ગુણોત્તરમાં વિભાજન કરે છે.
નોંધ : જો A, P અને B સમરેખ છે તેમ આપેલું હોય, તો PA અને PBનું અંતર શોધી PA અને PBનો ગુણોત્તર મેળવીને પણ આ ગુણોત્તર શોધી શકાય.
8. બિંદુઓ A (2, – 2) અને B(−7, 4)ને જોડતા રેખાખંડનાં ત્રિભાગ બિંદુઓ(અહીં બિંદુઓ રેખાખંડનું ત્રણ સમાન ભાગમાં વિભાજન કરે છે.)ના યામ શોધો.
ધારો કે, P અને Q એ ABને ત્રિભાગતાં બિંદુઓ છે.
જેથી AP = PQ = QB (જુઓ આકૃતિ)
માટે, P એ ABનું 1 : 2 ગુણોત્તરમાં અંતર્વિભાજન ક૨ે છે. આથી વિભાજન સૂત્રનો ઉપયોગ કરતાં,
આથી A અને Bને જોડતા રેખાખંડના ત્રિભાગ બિંદુઓના યામ (– 1, 0) અને (– 4, 2) થાય.
નોંધ : Q ને PB ના મધ્યબિંદુ તરીકે નિહાળીને પણ તેના યામ મેળવી શકાય. માટે મધ્યબિંદુના સૂત્રનો ઉપયોગ કરી તેના યામ મેળવી શકાય.
9. y-અક્ષ એ બિંદુઓ (5, – 6) અને (– 1, – 4)ને જોડતા રેખાખંડનું કયા ગુણોત્તરમાં વિભાજન કરે છે તે શોધો અને આ છેદબિંદુ પણ મેળવો.
ધારો કે, k : 1 માગેલ ગુણોત્તર છે. આથી વિભાજન સૂત્રની મદદથી ABનું k : 1માં વિભાજન કરતા બિંદુના યામ,
10. જો બિંદુઓ A (6, 1), B (8, 2), C (9, 4) અને D (p, 3) એ આ જ ક્રમમાં સમાંતરબાજુ ચતુષ્કોણનાં શિરોબિંદુઓ હોય, તો pની કિંમત શોધો.
સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો પરસ્પર દુભાગે છે.
આથી AC ના મધ્યબિંદુના યામ = BDના મધ્યબિંદુના યામ
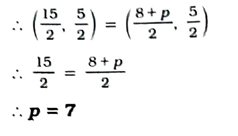
સ્વાધ્યાય – 7.2
1. બિંદુઓ ( − 1, 7) અને (4, − 3)ને જોડતા રેખાખંડનું 2 : 3 ગુણોત્તરમાં વિભાજન કરતા બિંદુના યામ શોધો.
ધારો કે, P (x, y) એ (−1, 7) અને (4, −3)ને જોડતા રેખાખંડનું 2 : 3 ગુણોત્તરમાં વિભાજન કરતું બિંદુ છે, તો વિભાજન સૂત્રનો ઉપયોગ કરતાં,
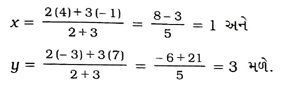
આમ, ( − 1, 7) અને (4, −3)ને જોડતા રેખાખંડનું 2 : 3 ગુણોત્તરમાં વિભાજન કરતાં બિંદુનાં યામ (1, 3) છે.
2. બિંદુઓ (4, − 1) અને ( – 2, – 3)ને જોડતા રેખાખંડના ત્રિભાગ બિંદુઓના યામ મેળવો.
ધારો કે, A (4, − 1) અને B(-2, −3) આપેલ બિંદુઓ છે તથા P અને Q એ રેખાખંડ ABના ત્રિભાગ બિંદુઓ છે.
3. તમારી શાળાના લંબચોરસ આકારના મેદાન ABCDમાં રમતગમત દિવસની પ્રવૃત્તિઓ યોજેલ છે. ચોક પાઉડરની મદદથી એક-એક મીટરના અંતરે રેખાઓ દોરેલી છે. આપેલ આકૃતિમાં દર્શાવ્યા અનુસાર AD પર પ્રત્યેક 1 મીટરના અંતરે હોય તેવા 100 ફૂલનાં કૂંડાં મૂક્યા છે.
નિહારિકા બીજી હરોળમાં દોડે છે અને તેણે AD નું 1/4 ભાગનું અંતર કાપ્યું છે અને ત્યાં લીલો ધ્વજ ફરકાવે છે. પ્રિત આઠમી હરોળમાં દોડે છે અને તેણે ADનું 1/5 ભાગ અંતર કાપ્યું છે અને ત્યાં લાલ ધ્વજ ફરકાવે છે. આ બંને ધ્વજ વચ્ચેનું અંતર કેટલું થશે? જો રશ્મિએ આ બંને ધ્વજને જોડતા રેખાખંડના મધ્યબિંદુ પર વાદળી ધ્વજ ફરકાવવાનો હોય, તો તે ધ્વજને ક્યાં ફરકાવશે?
આપણે લંબચોરસ ABCDને યામ-સમતલ તરીકે લઈએ, જેમાં બિંદુ A ઉગમબિંદુ થાય.
તો, AD = 100 મી અને દરેક મીટરના અંતરે દોરેલી રેખાઓ તેમનું x-અક્ષ પરનું અંતર દર્શાવે. નિહારિકા AD ના 1/4 ભાગનું અંતર કાપે છે.
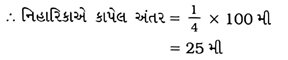
નિહારિકા બીજી રેખા પર દોડે છે.
આથી નિહારિકાએ જે સ્થાન પર લીલો ધ્વજ ફરકાવ્યો છે તે બિંદુ N ના યામ (2, 25) થાય.
તે જ પ્રમાણે, બિંદુ P કે જ્યાં પ્રિતે લાલ ધ્વજ ફરકાવ્યો છે તે બિંદુના યામ (8, 20) થાય.
બે ધ્વજ વચ્ચેનું અંતર (મીટરમાં) શોધવા માટે આપણે N (2, 25 ) અને P(8, 20)ને જોડતા રેખાખંડની લંબાઈ શોધવી પડે.
હવે, રશ્મિએ લીલા ધ્વજ અને લાલ ધ્વજનાં સ્થાનોને જોડતા રેખાખંડના મધ્યબિંદુ ૫૨ વાદળી ધ્વજ ફરકાવવાનો છે.
આથી આપણે N (2, 25) અને P (8, 20)ને જોડતા રેખાખંડ NP ના મધ્યબિંદુ R ના યામ મેળવવા જોઈએ.
મધ્યબિંદુ સૂત્રનો ઉપયોગ કરતાં, બિંદુ Rના યામ નીચે પ્રમાણે મળે :
આ દર્શાવે છે કે રશ્મિએ પાંચમી રેખા પ૨ ABથી 22.5 મી દૂર તેનો વાદળી ધ્વજ ફરકાવવો જોઈએ.
આમ, લીલા ધ્વજ અને લાલ ધ્વજ વચ્ચેનું અંતર √61 મી થાય અને રશ્મિએ તેનો વાદળી ધ્વજ પાંચમી રેખા પર ABથી 22.5 મી દૂર ફરકાવવો જોઈએ.
4. બિંદુ ( − 1, 6) બિંદુઓ (−3, 10) અને (6, – 8)ને જોડતા રેખાખંડનું કયા ગુણોત્તરમાં વિભાજન કરશે?
ધારો કે, બિંદુ P( − 1, 6) એ બિંદુઓ A ( – 3, 10) અને B (6, – 8) ને જોડતા રેખાખંડનું m1 : m2. ગુણોત્તરમાં વિભાજન કરે છે.
વિભાજન સૂત્રનો ઉપયોગ કરતાં,
આમ, બિંદુ ( – 1, 6) એ બિંદુઓ ( − 3, 10) અને (6, – 8)ને જોડતા રેખાખંડનું 2:7 ગુણોત્તરમાં વિભાજન કરશે.
5. x-અક્ષ બિંદુઓ A (1, − 5) અને B ( – 4, 5)ને જોડતા રેખાખંડનું કયા ગુણોત્તરમાં વિભાજન કરે છે તે શોધો. વિભાજન બિંદુના યામ પણ શોધો.
ધારો કે, x-અક્ષ બિંદુઓ A (1, − 5) અને B ( – 4, 5)ને જોડતા રેખાખંડનું k : 1 ગુણોત્તરમાં વિભાજન કરે છે.
તો, વિભાજન સૂત્ર મુજબ, રેખાખંડ ABનું k : 1 ગુણોત્તરમાં વિભાજન કરતા બિંદુના યામ નીચે પ્રમાણે મળે :
6. જો (1, 2), (4, y), (x, 6) અને (3, 5) એ એક સમાંતર- બાજુ ચતુષ્કોણનાં ક્રમિક શિરોબિંદુઓ હોય, તો x અને y શોધો.
A(1, 2), B (4, y), C (x, 6) અને D (3, 5) એ સમાંતરબાજુ ચતુષ્કોણ ABCDનાં શિરોબિંદુઓ છે.
ABCD સમાંતરબાજુ ચતુષ્કોણ હોવાથી તેના વિર્ણો AC અને BD પરસ્પર દુભાગે છે.
7. AB વર્તુળનો વ્યાસ છે. તેનું કેન્દ્ર (2, −3) અને B (1, 4) છે, તો બિંદુ Aના યામ શોધો.
ધારો કે, બિંદુ A ના યામ (x, y) છે.
વર્તુળનું કેન્દ્ર તેના દરેક વ્યાસનું મધ્યબિંદુ છે.
અહીં, AB વ્યાસ છે અને (2, −3) એ વર્તુળનું કેન્દ્ર છે.
8. જો A અને B અનુક્રમે (– 2, −2) અને (2, – 4) હોય, AP = 3/7 AB થાય અને બિંદુ P રેખાખંડ AB પર આવેલ હોય, તો તે બિંદુ P ના યામ શોધો.
A ( − 2, − 2) અને B (2, − 4) આપેલ બિંદુઓ છે. તથા બિંદુ P (x, y) એ AB ૫૨ આવેલ એવું બિંદુ છે કે જેથી AP = 3/7 AB થાય.
9. A ( – 2, 2) અને B (2, 8)ને જોડતા રેખાખંડનું ચાર સમાન ભાગમાં વિભાજન કરતા બિંદુઓના યામ શોધો.
10. સમબાજુ ચતુષ્કોણનાં ક્રમિક શિરોબિંદુઓ (3, 0), (4, 5), ( – 1, 4) અને ( – 2, − 1) હોય, તો તેનું ક્ષેત્રફળ શોધો.
મહત્ત્વનાં અન્ય ઉદાહરણો
1. બિંદુઓ ( – 2, 1) અને (4, 5)ને જોડતા રેખાખંડનું y-અક્ષ કયા ગુણોત્તરમાં વિભાજન કરે? વિભાજન બિંદુના યામ શોધો.
ધારો કે, y-અક્ષ બિંદુઓ ( – 2, 1) અને (4, 5)ને જોડતાં રેખાખંડનું k : 1 ગુણોત્તરમાં વિભાજન કરે છે.
વિભાજન સૂત્ર મુજબ, વિભાજન બિંદુના યામ નીચે મુજબ મળે :
2. Δ ABCની બાજુઓનાં મધ્યબિંદુઓના યામ (1, 1), (2, −3) અને (3, 4) છે. Δ ABCનાં શિરોબિંદુઓના યામ શોધો.
આમ, Δ ABCનાં શિરોબિંદુઓના યામ A (4, 0), B (2, 8) અને C (0, − 6) થાય.
નોંધ : આ પ્રકારના પ્રશ્નમાં કોઈ પણ શિરોબિંદુના યામ નીચેના સૂત્ર પરથી સહેલાઈથી મળે :
શિરોબિંદુ Aના યામ = ∠Aને સમાવતી બે બાજુઓનાં મધ્યબિંદુઓના યામનો સરવાળો – ∠ Aની સામેની બાજુના મધ્યબિંદુના યામ
3. સમાંતરબાજુ ચતુષ્કોણ ABCDનાં ત્રણ શિરોબિંદુઓ A (1, 2), B (2, 4) અને C (5, 9) છે. ચોથા શિરોબિંદુ Dના યામ શોધો.
ધારો કે, શિરોબિંદુ Dના યામ (x, y) છે.
ABCD સમાંતરબાજુ ચતુષ્કોણ હોવાથી તેના વિકર્ણો AC અને BD પરસ્પર દુભાગે.
આમ, ચોથા શિરોબિંદુ Dના યામ (4, 7) છે.
પાઠ્યપુસ્તકનાં ઉદાહરણો
11. જેનાં શિરોબિંદુઓ (1, − 1), (– 4, 6) અને (– 3, − 5) હોય તેવા ત્રિકોણનું ક્ષેત્રફળ શોધો.
A(1, − 1), B (− 4, 6) અને C(−3, –5) શિરોબિંદુઓ દ્વારા રચાતા ત્રિકોણનું ક્ષેત્રફળ શોધવા માટે ક્ષેત્રફળ સૂત્રનો ઉપયોગ કરતાં,
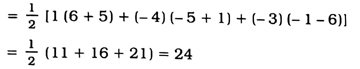
આથી ત્રિકોણનું ક્ષેત્રફળ 24 ચોરસ એકમ થાય.
12. બિંદુઓ A (5, 2), B (4, 7) અને C (7, – 4) દ્વારા રચાતા ત્રિકોણનું ક્ષેત્રફળ શોધો.
શિરોબિંદુઓ A (5, 2), B(4, 7) અને C (7, – 4) દ્વારા રચાતા ત્રિકોણનું ક્ષેત્રફળ
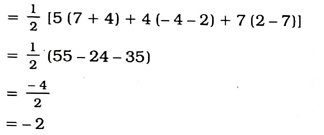
ક્ષેત્રફળ એ માપ હોવાથી તે ઋણ ન હોઈ શકે. આથી આપણે –2ની સંખ્યાત્મક કિંમત 2 લઈશું.
માટે ત્રિકોણનું ક્ષેત્રફળ = 2 ચોરસ એકમ.
13. બિંદુઓ P (– 1.5, 3), g (6, − 2) અને R – 3, 4)થી રચાતા ત્રિકોણનું ક્ષેત્રફળ શોધો.
આપેલ બિંદુઓથી રચાતા ત્રિકોણનું ક્ષેત્રફળ
જો ત્રિકોણનું ક્ષેત્રફળ ૦ ચોરસ એકમ હોય, તો તેનાં શિરોબિંદુઓ સમરેખ હોય. બીજા શબ્દોમાં, બિંદુઓ P, Q અને R સમ૨ેખ છે.
14. બિંદુઓ A (2, 3), B (4, k) અને C (6, – 3) સમરેખ હોય, તો ત્ની કિંમત શોધો.
આપેલ બિંદુઓ સમરેખ હોવાથી તેઓ દ્વારા રચાતા ત્રિકોણનું ક્ષેત્રફળ 0 જ થાય.
15. જો A (– 5, 7), B (– 4, − 5), C (- 1, – 6) અને D (4, 5) ક્રમમાં એ એક ચતુષ્કોણનાં શિરોબિંદુઓ હોય, તો ચતુષ્કોણ ABCDનું ક્ષેત્રફળ શોધો.
Bથી Dને જોડવાથી, તમને ABD અને BCD બે ત્રિકોણો મળશે.
[નોંધ : બહુકોણનું ક્ષેત્રફળ શોધવા માટે, આપણે જેમાં સામાન્ય ક્ષેત્રફળ ન હોય તેવા ત્રિકોણીય પ્રદેશોમાં વિભાજન કરીએ અને તેનું ક્ષેત્રફળ આ પ્રદેશોનાં ક્ષેત્રફળોનો સરવાળો કરવાથી મળે.]
સ્વાધ્યાય – 7.3
1. જેનાં શિરોબિંદુઓ નીચે પ્રમાણે છે તેવા ત્રિકોણનું ક્ષેત્રફળ શોધો :
(1) (2, 3), (-1, 0), (2, -4)
(2) (-5, 1), (3, -5), (5, 2)
2. નીચે આપેલાં હિંદુઓ સમરેખ હોય તો પ્રત્યેકમાં ‘ની કિંમત શોધો :
(1) (7.-2), (5, 1), (3, k)
(2) (8, 1), (k.-4), (2,-5)
( 1 ) જો હિંદુઓ (7, −2), (5, 1) અને (3, k) સમરેખ હોય, તો તેમના દ્વારા બનતા કાલ્પનિક ત્રિકોણનું ક્ષેત્રફળ શુન્ય જ થાય.
( 2 ) જો બિંદુઓ(8, 1), (k, − 4) અને (2, 5) સમરેખ હોય, તો તેમના દ્વારા બનતા કાલ્પનિક ત્રિકોણનું ક્ષેત્રફળ શૂન્ય જ થાય.
3. જેનાં શિરોબિંદુઓ (0, − 1), (2, 1) અને (0, 3) હોય, તેવા ત્રિકોણની બાજુઓનાં મધ્યબિંદુઓને જોડવાથી બનતા ત્રિકોણનું ક્ષેત્રફળ શોધો. આ ત્રિકોણનું ક્ષેત્રફળ અને આપેલ ત્રિકોણના ક્ષેત્રફળનો ગુણોત્તર શોધો.
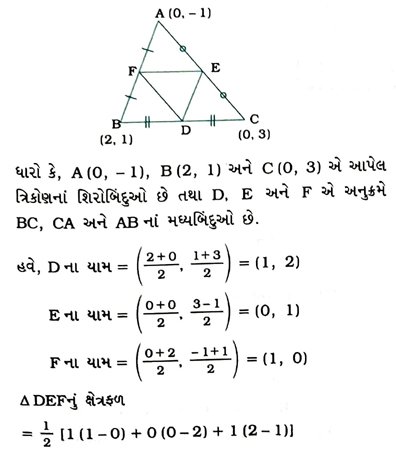
આમ, આપેલ શિરોબિંદુઓવાળા ત્રિકોણની બાજુઓના મધ્યબિંદુઓને જોડવાથી મળતા ત્રિકોણનું ક્ષેત્રફળ 1 ચોરસ એકમ થાય અને માગેલ ગુણોત્તર 1 : 4 થાય.
4. એક ચતુષ્કોણનાં ક્રમિક શિરોબિંદુઓ (– 4, − 2), (– 3, − 5), (3, − 2) અને (2, 3) હોય, તો તેનું ક્ષેત્રફળ શોધો.
5. તમે ધોરણ IX(પ્રકરણ 9, પ્રશ્ન નં. ૩)માં શીખ્યા છો કે ત્રિકોણની મધ્યગા ત્રિકોણનું બે સમાન ક્ષેત્રફળવાળા ત્રિકોણમાં વિભાજન કરે છે. જેનાં શિરોબિંદુઓ A (4, – 6), B (3, – 2) અને C (5, 2) હોય તેવા Δ ABC માટે આ પરિણામ ચકાસો.
આમ, મધ્યગા AD દ્વારા Δ ABCનું બે સમાન ક્ષેત્રફળ ધરાવતા ત્રિકોણો, Δ ADB અને Δ ADCમાં વિભાજન થાય છે.
આ પ્રમાણે જ, મધ્યગાઓ BE અને CF માટે પણ ઉપરોક્ત પરિણામ સાબિત કરી શકાય.
આમ, ‘ત્રિકોણની મધ્યગા ત્રિકોણનું બે સમાન ક્ષેત્રફળવાળા ત્રિકોણમાં વિભાજન કરે છે.” એ વિધાન સત્ય પુરવાર થાય છે.
મહત્ત્વનાં અન્ય ઉદાહરણો
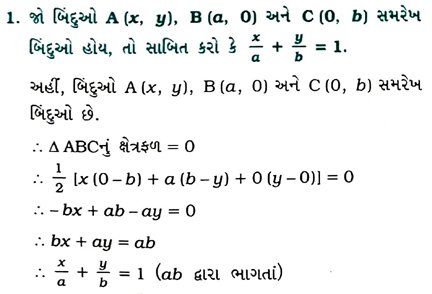
2. A (– 2, k), B (3, – 4 ) અને C (7, 10) એ સમઢિભુજ કાટકોણ Δ ABC નાં શિરોબિંદુઓ છે, જેમાં ∠ A = 90°. kની કિંમત તથા Δ ABC નું ક્ષેત્રફળ શોધો.
3. Δ ABCનું ક્ષેત્રફળ 5 ચોરસ એકમ છે. તેનાં બે શિરોબિંદુઓ A (2, 1 ) તથા B (3, – 2) છે. અને ત્રીજું શિરોબિંદુ C રેખા y − x + 3 = 0 પર આવેલ છે. શિરોબિંદુ Cના યામ શોધો.
ધારો કે, ત્રીજું શિરોબિંદુ C (a, b) છે.
Δ ABCનું ક્ષેત્રફળ = 5 (આપેલ છે.)
સ્વાધ્યાય – 7.4
- આ સ્વાધ્યાય પરીક્ષા માટે ધ્યાનમાં લેવાનો નથી.
1. રેખા 2x + y – 4 = 0 એ બિંદુઓ A (2, − 2) અને B (3, 7)ને જોડતા રેખાખંડનું કયા ગુણોત્તરમાં વિભાજન કરશે તે નક્કી કરો.
ધારો કે, રેખા 2x + y − 4 = 0 એ બિંદુઓ A (2, – 2) અને B (3, 7)નું બિંદુ M (a, b) પર k : 1 ગુણોત્તરમાં વિભાજન કરે છે.
આમ, રેખા 2x + y – 4 = 0 એ બિંદુઓ A (2, – 2) અને B (3, 7)ને જોડતા રેખાખંડનું 2 : 9 ગુણોત્તરમાં વિભાજન ક૨શે.
2. જો બિંદુઓ (x, y), (1, 2) અને (7, 0) સમરેખ હોય, તો x અને y વચ્ચેનો સંબંધ મેળવો.
3. બિંદુઓ (6, – 6), (3, –7) અને (3, 3)માંથી પસાર થતા વર્તુળનું કેન્દ્ર શોધો.
ધારો કે, P (x, y) એ આપેલ બિંદુઓ A (6, – 6), B (3, – 7) અને C (3, 3)માંથી પસાર થતા વર્તુળનું કેન્દ્ર છે. આથી P એ A, B અને C ત્રણેયથી સમાન અંતરે છે.
∴ PA = PB = PC
4. ચોરસનાં બે સામસામેનાં શિરોબિંદુઓ (– 1, 2) અને (3, 2) છે, તો બાકીનાં બે શિરોબિંદુઓના યામ શોધો.
ધારો કે, ABCD આપેલ ચોરસ છે, જેનાં સામસામેનાં બે શિરોબિંદુઓ A (− 1, 2) અને C (3, 2) છે. આપણે શિરોબિંદુઓ B અને D શોધવાના છે.
ધારો કે, Bના યામ (x, y) છે.
Δ ABCમાં, ∠B = 90° અને AB = BC.
∴ AB2 = BC2
અહીં, આપણને નું એક જ મૂલ્ય મળે છે, પરંતુ પુનાં બે મૂલ્યો મળે છે, જે સૂચવે છે કે B અને Dના x-યામ સમાન છે પરંતુ પુ-યામ જુદા છે.
આમ, બાકીનાં બે શિરોબિંદુઓના યામ (1, 0) અને (1, 4) છે.
5. કૃષિનગરની માધ્યમિક શાળાના ધોરણ Xના વિદ્યાર્થીઓને બાગાયત પ્રવૃત્તિ માટે એક લંબચોરસ મેદાન ફાળવવામાં આવ્યું છે. તેની ફરતી બાજુએ ગુલમહોરના રોપા એક-એક મીટરના અંતરે વાવેલા છે. આપેલ આકૃતિમાં દર્શાવ્યા પ્રમાણે આ મેદાનમાં ઘાસની એક ત્રિકોણીય લોન છે. વિદ્યાર્થીઓને બાકીના ભાગ પર ફૂલોના છોડના બીજ વાવવાનાં છે.
( 1 ) Aને ઉગમબિંદુ લઈ ત્રિકોણનાં શિરોબિંદુઓના યામ શોધો.
( 2 ) જો C ઉગમબિંદુ હોય, તો A PORનાં શિરોબિંદુઓના યામ શું થાય? આ બંને કિસ્સાઓમાં ત્રિકોણનું ક્ષેત્રફળ શોધો. તમે શું અવલોકન કર્યું?
( 1 ) Aને ઉગમબિંદુ તથા AB અને ADને અનુક્રમે y-અક્ષ અને x-અક્ષ લેતાં, આપણને લંબચોરસ મેદાનનાં શિરોબિંદુઓના યામ A (0, 0), B (0, 8), D (16, 0) અને C (16, 8) મળે.
તે જ પ્રમાણે, યામ-સમતલ પરથી A PORનાં શિરોબિંદુઓ ),
P (4, 6) Q (3, 2) અને R (6, 5) મળે.
( 2 ) Cને ઉગમબિંદુ તથા CB અને CDને અનુક્રમે ધન x-અક્ષ અને ધન y-અક્ષ લેતાં, આપણને લંબચોરસ મેદાનનાં શિરોબિંદુઓના યામ C (0, 0), B (16, 0), D (0, 8) અને A ( 16, 8) મળે.
તે જ પ્રમાણે, યામ-સમતલ ૫૨થી A PQRનાં શિરોબિંદુઓ
P (12, 2), Q (13, 6) અને R (10, 3) મળે.
આપણે સ્પષ્ટ રીતે જોઈ શકીએ છીએ કે બંને કિસ્સાઓમાં Δ PQRનું ક્ષેત્રફળ સમાન છે.
[નોંધ : બીજા કિસ્સામાં જો આપણે CB અને CDને અનુક્રમે ઋણ x-અક્ષ અને ઋણ y-અક્ષ લઈએ, તો Δ PQRનાં શિરોબિંદુઓનાં યામ P (− 12, − 2), Q (− 13, − 6) અને R (− 10, − 3) થાય. તેમ છતાં, Δ PQRનું ક્ષેત્રફળ તો ન જ ફેરવાય.]
6. Δ ABCનાં શિરોબિંદુઓ A (4, 6), B (1, 5) અને C (7, 2) છે. બાજુઓ AB અને ACને અનુક્રમે એક રેખા D અને Eમાં એવી રીતે છેદે છે જેથી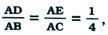 
તો ΔADEનું ક્ષેત્રફળ મેળવો અને Δ ABCના ક્ષેત્રફળ સાથે તેની તુલના કરો. (પ્રમેય 6.2 અને પ્રમેય 6.6 યાદ કરો.)
તો ΔADEનું ક્ષેત્રફળ મેળવો અને Δ ABCના ક્ષેત્રફળ સાથે તેની તુલના કરો. (પ્રમેય 6.2 અને પ્રમેય 6.6 યાદ કરો.)
7. A (4, 2), B (6, 5) અને C (1, 4) એ AABCનાં શિરોબિંદુઓ છે.
( 1 ) Aમાંથી દોરેલ મધ્યગા BCને Dમાં મળે છે. બિંદુ Dના યામ શોધો.
( 2 ) AP : PD = 2 : 1 થાય એવું બિંદુ P એ AD પર છે, તો Pના યામ શોધો.
( 3 ) BQ : QE = 2 : 1 અને CR : RF = 2 : 1 હોય તેવાં બિંદુઓ Q અને R અનુક્રમે મધ્યગા BE અને CF પર છે, તો છુ અને Rના યામ શોધો.
( 4 ) તમે શું અવલોકન કર્યું?
( 5 ) જો A (x1, y1), B (x2, y2) અને C (x3, y3) એ Δ ABCનાં શિરોબિંદુઓ હોય તો આપેલ ત્રિકોણના મધ્યકેન્દ્રના યામ શોધો.
[નોંધ : ત્રણેય મધ્યગાઓના છેદબિંદુને મધ્યકેન્દ્ર કહે છે અને તે દરેક મધ્યગાનું 2: 1 ગુણોત્તરમાં વિભાજન કરે છે.]
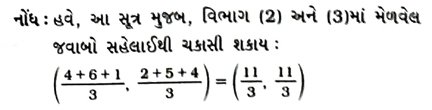
8. બિંદુઓ A ( – 1, − 1), B (- 1, 4), C (5, 4) અને D (5, – 1)થી લંબચોરસ ABCD રચાય છે. P, Q, R અને S અનુક્રમે AB, BC, CD અને DAનાં મધ્યબિંદુઓ છે. ચતુષ્કોણ PQRS ચોરસ છે? લંબચોરસ છે? કે સમબાજુ ચતુષ્કોણ છે? તમારો જવાબ ચકાસો.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
(1) બિંદુ (– 6, 8)નું ઉગમબિંદુથી અંતર …….. એકમ હોય.
(2) (0, 4), (0, 0) અને (3, 0) શિરોબિંદુઓ ધરાવતા ત્રિકોણની પરિમિતિ ……. એકમ થાય.
(3) (3, 0), (7, 0) અને (8, 4) શિરોબિંદુઓ ધરાવતા ત્રિકોણનું ક્ષેત્રફળ …… ચોરસ એમ થાય.
( 4 ) (7, − 6) અને (3, 4)ને જોડતા રેખાખંડનું 1 : 2 ગુણોત્તરમાં વિભાજન કરતું બિંદુ ……. ચરણમાં હોય.
(5) A (0, 5), B(3, 0) અને C (3, 5) શિરોબિંદુઓ ધરાવતો Δ ABC …….. ત્રિકોણ છે.
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
(1) જો બિંદુઓ (a, 0), (0, b) અને (1, 1) સમરેખ બિંદુઓ હોય, તો 1/a + 1/b = …….
A. 1
B. 2
C. 0
D. – 1
(2) (7, x), (y, −6) અને (9, 10) શિરોબિંદુઓ ધરાવતા ત્રિકોણનું મધ્યકેન્દ્ર (6, 3) હોય, તો (x, y) = …….
A. (4, 5)
B. (5, 4)
C. (– 5, – 2)
D. (5, 2)
(3) y-અક્ષ બિંદુઓ A (a1, b1) અને B (a2, b2)ને જોડતાં ……. રેખાખંડનું ગુણોત્તરમાં વિભાજન કરે છે.
A. – a1 : a2
B. a1 : a2
C. b1 : b2
D. – b1 : b2
(4) એક રેખાખંડની લંબાઈ 10 એકમ છે. તેનાં એક અંત્યબિંદુના યામ (2, −3) છે અને બીજા અંત્યબિંદુનો કોટિ 10 હોય તો તેનો ભુજ …….. હોય.
A. 9 અથવા 6
B. 3 અથવા −9
C. – 3 અથવા 9
D. 9 અથવા – 6
(5) જો A (2,2), B (– 4, −4) અને એ C (5, -8) Δ ABCનાં શિરોબિંદુઓ હોય, તો Cમાંથી દોરેલ Δ ABCની મધ્યગાની લંબાઈ …… એકમ થાય.
A. √65
B. √117
C. √85
D. √113
(6) જો બિંદુ P (x, y) એ બિંદુઓ A (5, 1) અને B (– 1, 5)થી સમાન અંતરે હોય, તો …… સાચું છે.
A. 5x = y
B. x = 5y
C. 3x = 2y
D. 2x = 3y
(7) જો (0, 0), (2, 0) અને (0, 3) એ કોઈ લંબચોરસનાં ત્રણ શિરોબિંદુઓ હોય, તો તેનું ચોથું શિરોબિંદુ ……. છે.
A. (3, 0)
B. (0, 2)
C. (2, 3)
D. (3, 2)
(8) જો ઉગમબિંદુ કેન્દ્ર હોય અને ત્રિજ્યા 5 એકમ હોય તેવા વર્તુળનું એક બિંદુ (x, 4) હોય, તો x=………..
A. ±5
B. ±3
C. O
D. ±4
(9) A (1, 3) અને B (4, 6)ને જોડતા રેખાખંડનું 2:1 ગુણોત્તરમાં વિભાજન કરતાં બિંદુ ના યામ …… છે.
A. (2, 4)
B. (3, 5)
C. (4, 2)
D. (5, 3)
(10) જો P (2, 4), Q(0, 3), R (3, 6) અને S (5, y) એ સમાંતરબાજુ ચતુષ્કોણ PQRSનાં શિરોબિંદુઓ હોય, તો y = …….
A. 7
B. 5
C.−7
D. – 8
3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ આપો :
(1) A (5, − 2) અને B (7, 10)ને જોડતા રેખાખંડના મધ્યબિંદુના યામ શોધો.
(2) (0, 0), (5, 0) અને (0, 12) શિરોબિંદુઓ ધરાવતા ત્રિકોણનું ક્ષેત્રફળ શોધો.
(3) (5, 18), (4, 3) અને (3, −3) શિરોબિંદુઓ ધરાવતા ત્રિકોણના મધ્યકેન્દ્રના યામ જણાવો.
(4) બિંદુ (20, 21)નું ઉગમબિંદુથી અંતર શોધો.
(5) A (5, 6) અને B (2, −8)નું x-અક્ષ દ્વારા ક્યા ગુણોત્તરમાં વિભાજન થાય છે?
(6) Q (– 6, 7) અને R (− 2, 3)ને જોડતા રેખાખંડનું મધ્યબિંદુ A(m/2, 5) હોય, તો m ની કિંમત શોધો.
(7) P (– 3, 2)માંથી પુ-અક્ષ પર દોરેલા લંબનો લંબપાદ M છે, તો બિંદુ Mના યામ જણાવો.
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
(1) બિંદુઓ (0, 5), (0, −9) અને (3, 6) સમરેખ છે. =
(2) બિંદુ A (2, 7) એ P (6, 5) અને Q(0, – 4)ને જોડતા રેખાખંડ POના લંબદ્વિભાજક પ૨ આવેલ બિંદુ છે.
(3) બિંદુ P (– 4, 2) એ A (– 4, 6) અને B (– 4, − 6)ને જોડતા રેખાખંડ પરનું બિંદુ છે.
(4) બિંદુઓ A (3, 1), B(12, −2) અને C (0, 2) એ કોઈ ત્રિકોણનાં શિરોબિંદુઓ ન હોઈ શકે.
(5) એક વર્તુળનું કેન્દ્ર ઉગમબિંદુ છે અને બિંદુ P (5, 0) વર્તુળ પરનું બિંદુ છે, તો બિંદુ Q (3, 4) વર્તુળના અંદરના ભાગમાં હોય.
જવાબ : 1. ( 1 ) 10 (2) 12 (3)8 (4 ) ચતુર્થ ( 5 ) કાટકોણ અથવા વિષમભુજ
2. (1) 1 (2) (5, 2) (3)-a₁ a2 (4) 324-9 (5) √85 (6) 3x = 2y (7) (2, 3) (8) ±3 (9)(3, 5) (10) 7
3. ( 1 ) (6,4)( 2 ) 30 ચોરસ એકમ (3) (4, 6) ( 4 ) 29 એકમ ( 5 ) 3 : 4 ( 6 ) – 8 ( 7 ) (0, 2)
4. ( 1 ) ખોટું ( 2 ) ખોટું ( 3 ) ખરું ( 4 ) ખરું ( 5 ) ખોટું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here