Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 9 Some Applications of Trigonometry (ત્રિકોણમિતિના ઉપયોગો)
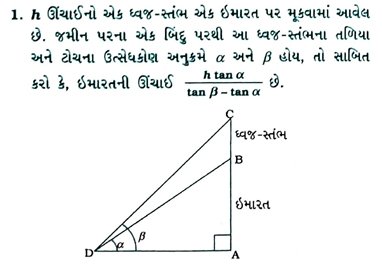
Gujarat Board | Class 10Th | Mathematics | Model Question Paper & Solution | Chapter – 9 Some Applications of Trigonometry (ત્રિકોણમિતિના ઉપયોગો)
સ્વાધ્યાય – 9.1
1. સર્કસના તંબુમાં, જમીન સાથે શિરોલંબ સ્થિતિમાં રહેલા થાંભલાની ટોચથી જમીન સાથે ખેંચીને બાંધેલા 20 મી લાંબા દોરડા પર એક કલાકાર ચડી રહ્યો છે. જો દોરડું જમીન સાથે 30° માપનો ખૂણો બનાવે, તો થાંભલાની ઊંચાઈ શોધો. (જુઓ આકૃતિ).

2. વાવાઝોડાને કારણે એક ઝાડ એ રીતે ભાંગીને વળી જાય છે, જેથી તેની ટોચ, જમીન સાથે 30° માપનો ખૂણો બનાવે તે રીતે જમીનને સ્પર્શે છે. ઝાડની જમીનને સ્પર્શતી ટોચ અને ઝાડના થડ વચ્ચેનું અંતર 8મી હોય, તો ઝાડની ઊંચાઈ શોધો.


3. એક ટંકાર બાળકોને રમવા માટે, બગીચામાં બે લપસણી લગાવવાની છે. આ માટે તે 5 વર્ષથી ઓછી ઉંમરનાં બાળકો માટે જમીનથી ઉપરનો ઠંડી 1.5 મી રહે અને જમીન સાથે 30નો ખૂણો બનાવે તેવી અને તેનાથી વધારે ઉંમરનાં બાળકો માટે ૩ મીની ઊંચાઇથી સીધો ઢાળ હોય તથા જમીન સાથે 60નો ખૂણો બનાવતી હોય તેવી લપસણી પસંદ કરે છે, તો બંને લપસણીઓની લંબાઈ શોધો.

તે જ રીતે, DF એ 5 વર્ષથી વધારે ઉંમરનાં બાળકો માટેની લપસણી દર્શાવે છે.

આમ, 5 વર્ષથી ઓછી ઉંમરનાં બાળકો માટેની લપસણીની લંબાઈ 3 મી અને તેનાથી વધારે ઉંમરનાં બાળકો માટેની લપસણીની લંબાઈ 2√3 મી થાય.
4. ટાવરના પાયાથી 30 મી દૂર રહેલા જમીન પરના એક બિંદુથી ટાવરની ટોચના ઉત્સેધકોણનું માપ 30॰ છે, તો ટાવરની ઊંચાઈ શોધો.

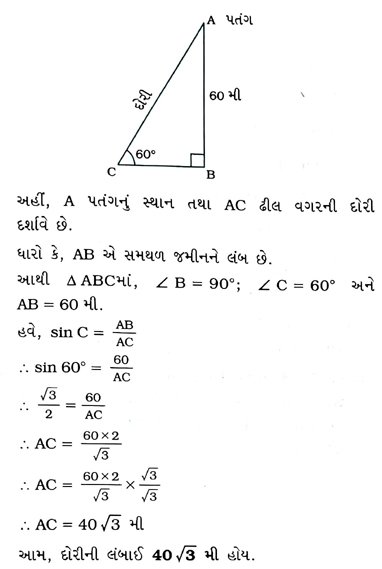
5. એક પતંગ જમીનથી 60 મીની ઊંચાઈ પર ઊડી રહેલ છે. આ પતંગની દોરીનો એક છેડો ક્ષણભર માટે જમીન પરના એક બિંદુ સાથે બાંધેલ છે. આ સ્થિતિમાં દોરીનો જમીન સાથેનો ખૂણો 60° છે. જો દોરીમાં કોઈ ઢીલ નથી તેવું માની લેવામાં આવે, તો દોરીની લંબાઈ શોધો.
6. 1.5 મી ઊંચો એક છોકરો એક 30 મી ઊંચી ઇમારતથી કોઈક અંતરે ઊભેલ છે. હવે જ્યારે તે ઇમારત તરફ ચાલવાનું શરૂ કરે છે ત્યારે કેટલાક સમય પછી તેની આંખથી ઇમારતની ટોચના ઉત્સેધકોણનું માપ 30થી વધીને 60° થાય છે, તો તે કેટલું અંતર ચાલ્યો હશે ?
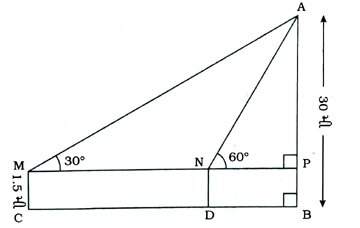
અહીં, AB ઇમારત દર્શાવે છે. C એ છોકરાનું શરૂઆતનું સ્થાન તથા D એ છોકરાનું અંતિમ સ્થાન દર્શાવે છે. વળી, M અને N એ બે સ્થાન પરની પરિસ્થિતિમાં છોકરાની આંખો દર્શાવે છે. ધારો કે, લંબાવેલ MN, ABને Pમાં મળે છે.
આથી Δ APNમાં, ∠ P = 90°; ∠ N = 60° તથા Δ APMમાં, ∠ P = 90° અને ∠ M = 30°.

7. જમીન પર આવેલ એક બિંદુથી એક 20 મી ઊંચી ઇમારતની ટોચ પર રહેલ એક સંચાર ટાવરના તળિયા અને ટોચના ઉત્સેધકોણનાં માપ અનુક્રમે 45° અને 60° છે, તો ટાવરની ઊંચાઈ શોધો.
અહીં, AB સંચાર ટાવર, BC ઇમારત અને D નિરીક્ષણ બિંદુ દર્શાવે છે.

8. એક ઊંચી બેઠક પર 1.6 મી ઊંચી એક પ્રતિમા ગોઠવેલ છે. જમીન પરના એક બિંદુએથી પ્રતિમાની ટોચના ઉત્સેધકોણનું માપ 60° અને બેઠકની ટોચના ઉત્સેધકોણનું માપ 45° છે, તો બેઠકની ઊંચાઈ શોધો.


9. એક ટાવરના તળિયાથી એક ઇમારતની ટોચના ઉત્સેધકોણનું માપ 30° છે અને ઇમારતના તળિયાથી ટાવરની ટોચના ઉત્સેધકોણનું માપ 60° છે. જો ટાવરની ઊંચાઈ 50 મી હોય, તો ઇમારતની ઊંચાઈ શોધો.


10. એક 80 મી પહોળા માર્ગની બંને બાજુએ સમાન ઊંચાઈના બે સ્તંભ શિરોલંબ સ્થિતિમાં છે. માર્ગ પર વચ્ચે આવેલ કોઈ એક બિંદુએથી બંને સ્તંભની ટોચના ઉત્સેધકોણનાં માપ 60° અને ૩0° જણાય છે. તો દરેક સ્તંભની ઊંચાઈ શોધો તથા બંને સ્તંભનું નિરીક્ષણ હિંદુથી અંતર શોધો.
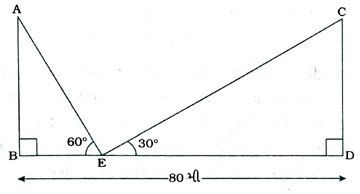
અહીં, AB અને CD સમાન ઊંચાઈના બે સ્તંભ દર્શાવે છે. BD એ 80 મી પહોળો માર્ગ દર્શાવે છે તથા બિંદુ E એ માર્ગ પરનું નિરીક્ષણ સ્થાન દર્શાવે છે.


આમ, દરેક સ્તંભની ઊંચાઈ 20√3 મી છે, નિરીક્ષણ સ્થાનનું નજીકના સ્તંભથી અંતર 20 મી છે તથા તેનું બીજા સ્તંભથી અંતર 60 મી છે.
11. નહેરના એક કિનારા પર ટીવીનો ટાવર શિરોલંબ ઊભો કરવામાં આવેલ છે. ટાવરની સામેના બીજા કિનારા પર રહેલા એક બિંદુથી ટાવરની ટોચનો ઉત્સેધકોણ 60° છે. ટાવરના તળિયા અને નિરીક્ષણ બિંદુને જોડતી રેખા પર આવેલ અને નિરીક્ષણ બિંદુથી 20 મી દૂર બીજા એક બિંદુથી ટાવરની ટોચના ઉત્સેધકોણનું માપ 30° છે (જુઓ આકૃતિ), તો ટાવરની ઊંચાઈ અને નહેરની પહોળાઈ શોધો.
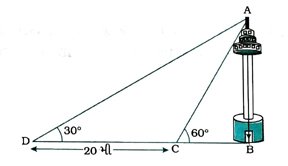
અહીં, AB ટીવીનો ટાવર, BC એ નહેરની પહોળાઈ તથા C અને D એકબીજાથી 20 મી દૂર આવેલાં એવાં નિરીક્ષણ બિંદુઓ છે કે જેથી D, C અને B સમરેખ થાય.
આથી Δ ABCમાં, ∠ B = 90° અને ∠ C = 60° તથા Δ ABDમાં, ∠ B = 90° અને Δ D = 30° થાય, તેમજ CD = 20 મી થાય.
ધારો કે, ટાવરની ઊંચાઈ = AB = h મી અને નહેરની પહોળાઈ = BC = x મી. આથી BD = BC + CD = (x + 20) મી થાય.

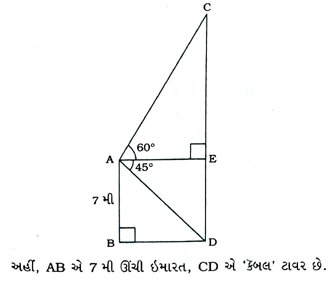
12. 7 મી ઊંચી ઇમારત પરથી એક ‘બલ’ ટાવરની ટોચનો ઉત્સેધકોણ 60° અને ટાવરના તળિયાનો અવસેધકોણ 45° છે, તો ટાવરની ઊંચાઈ શોધો.

13. દરિયાની સપાટીથી 75 મી ઊંચી દીવાદાંડી પરથી અવલોકન કરતાં, દરિયામાં રહેલાં બે વહાણના અવસેધકોણનાં માપ 30° અને 45° માલૂમ પડે છે. જો એક વહાણ બીજાની બરાબર પાછળ હોય અને બંને વહાણ દીવાદાંડીની એક જ બાજુ પર આવેલ હોય, તો બંને વહાણ વચ્ચેનું અંતર શોધો.


14. 1.2 મી ઊંચાઈવાળી એક છોકરીને, જમીનથી 88.2 મી ઊંચાઈ પર રહેલું પવનને કારણે સમક્ષિતિજ રેખામાં ગતિ કરતું એક બલૂન જોવા મળે છે. કોઈ એક સમયે છોકરીને તેના ઉત્સેધકોણનું માપ 60° મળે છે. થોડા સમય બાદ બલૂનના ઉત્સેધકોણનું માપ 30° થાય છે (જુઓ આકૃતિ), તો આ સમય દરમિયાન બલૂને કાપેલું અંતર શોધો.


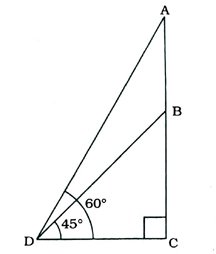
15. એક સુરેખ માર્ગ ટાવર તરફ જાય છે. ટાવરની ટોચ પર રહેલ એક વ્યક્તિ, ટાવર તરફ અચળ ઝડપથી આવતી એક મોટરકારના અવસેધકોણનું માપ 30° નોંધે છે. 6 સેકન્ડ પછી આ કારના અવસેધકોણનું માપ 60° થાય છે, તો કારને ટાવર સુધી પહોંચતાં કેટલો સમય લાગશે?


આમ, મોટરકારને તેના દ્વિતીય સ્થાનથી ટાવર સુધી પહોંચતા 3 સેકન્ડ લાગશે.
16. ટાવરના તળિયામાંથી પસાર થતી રેખા પર તળિયાથી 4 મી અને 9 મી દૂર આવેલાં બે બિંદુથી ટાવરની ટોચના ઉત્સેધકોણનાં માપ કોટિકોણનાં માપ છે. સાબિત કરો કે, ટાવરની ઊંચાઈ 6 મી છે.
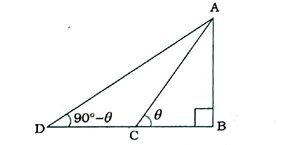
અહીં, AB ટાવર છે. C એ ટાવરના તળિયાથી 4 મી દૂર આવેલ નિરીક્ષણ બિંદુ છે અને D એ ટાવરના તળિયાથી 9 મી દૂર આવેલ નિરીક્ષણ બિંદુ છે.

મહત્ત્વનાં અન્ય ઉદાહરણો



3. એક ગોળાકાર બલૂન, કે જેની ત્રિજ્યા r છે, તે એક નિરીક્ષકની આંખ પર નો ખૂણો આંતરે છે. જો તે નિરીક્ષક માટે બલૂનના કેન્દ્રનો ઉત્સેધકોણ ø હોય, તો બલૂનના કેન્દ્રની જમીનથી ઊંચાઈ શોધો.

અહીં, O એ બલૂનનું કેન્દ્ર છે. A એ નિરીક્ષક છે. ∠ PAQ એ બલૂન દ્વારા નિરીક્ષકની આંખ પર આંતરાતો ખૂણો છે. OP એ બલૂનની ત્રિજ્યા છે. OB એ બલૂનના કેન્દ્રની જમીનથી ઊંચાઈ આપે છે.

હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને એ રીતે નીચેનાં વિધાનોમાં ખાલી જગ્યા પૂરો :
( 1 ) એક પતંગ 75 મીની ઊંચાઈ પર ઊડી રહ્યો છે અને તેની તંગ દોરી સમક્ષિતિજ સાથે 60°નો ખૂણો બનાવે છે, તો દોરીની લંબાઈ …… મી હોય.
( 2 ) દીવાલના ટેકે મૂકેલ એક નિસરણી જમીન સાથે 60નો ખૂણો બનાવે છે. જો નિસરણીનો નીચેનો છેડો દીવાલથી 8 મી દૂર હોય, તો નિસરણીની લંબાઈ …… મી છે.
( 3 ) એક ટાવરથી 30 મીના અંતરે આવેલ જમીન પરના એક બિંદુ પરથી ટાવરની ટોચનો ઉત્સેધકોણ 30° છે, તો ટાવરની ઊંચાઈ ……. મી હોય.
( 4 ) જ્યારે એક વ્યક્તિની ઊંચાઈ તથા તેના પડછાયાની લંબાઈ સરખી હોય ત્યારે સૂર્યનો ઉત્સેધકોણ ……… હોય.
( 5 ) એક ટાવરની ઊંચાઈ 200 મી છે. જ્યારે સૂર્યનો ઉત્સેધકોણ 30° હોય ત્યારે ટાવરના પડછાયાની લંબાઈ …….. મી હોય.
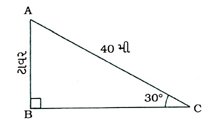
( 6 ) નીચેની આકૃતિમાં ટાવર (AB)ની ઊંચાઈ …….. મી છે.
2. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો :
( 1 ) 15 મી ઊંચા એક ટાવરના તળિયાથી 15 મી દૂર આવેલ જમીન પરના એક બિંદુથી ટાવરની ટોચનો ઉત્સેધકોણ ……. થાય.
A. 30°
B. 60°
C. 45°
D. 75°
( 2 ) 50 મી ઊંચાઈના એક પુલ પરથી એક હોડીનો અવસેધકોણ 30° છે. આથી, હોડીનું પુલથી સીધું અંતર ……. મી હોય.
A. 50 √3
B. 50
C. 25√3
D. 25
( 3 ) એક વૃક્ષની ટોચ પર એક પક્ષી બેઠેલ છે. વૃક્ષના તળિયાથી 20 મી દૂર આવેલ જમીન પરના એક બિંદુએથી નિરીક્ષણ કરતાં તે પક્ષીનો ઉત્સેધકોણ 60॰ જણાય છે, તો વૃક્ષની ઊંચાઈ ……. મી છે.
A. 20√3
B. 10√3
C. 20
D. 10
( 4 ) જ્યારે સૂર્યનો ઉત્સેધકોણ 30° હોય ત્યારે 10 મી ઊંચાઈના એક વૃક્ષના પડછાયાની લંબાઈ ……. મી થાય.
A. 10
B. 10/√3
C. 10√3
D. 20
( 5 ) 16 મી અને 10 મી ઊંચાઈવાળા બે સ્તંભની ટોચ વચ્ચે એક તાર બાંધેલ છે. જો તાર સમક્ષિતિજ રેખા સાથે 30નો ખૂણો બનાવે, તો તારની લંબાઈ ……. મી હોય.
A. 26
B. 16
C. 12
D. 10
( 6 ) જમીન પરના એક બિંદુ Pથી એક ટાવરની ટોચનો ઉત્સેધકોણ α છે. Pથી ટાવર તરફ dમી અંતર ચાલ્યા બાદ ટાવરની ટોચનો ઉત્સેધકોણ β છે, તો …….. સાચું છે.
A. α < β
B. α > β
C. α = β
D. આપેલ પૈકી એક પણ નહીં
( 7 ) 1.8 મી ઊંચાઈવાળી એક છોકરી લાઇટના થાંભલાથી 4.6 મી દૂર ઊભી હોય ત્યારે તેના પડછાયાની લંબાઈ 5.4મી છે. આથી લાઇટના થાંભલામાં મૂકેલ ગોળો જમીનથી ……… મીની ઊંચાઈ પર છે.
A. 1.53
B. 10/3
C. 13.8
D. 0.8
( 8 ) એક ટાવરના તળિયાથી 500 મી દૂર આપેલાં એક બિંદુથી ટાવરની ટોચનો ઉત્સેધકોણ 30° છે, તો ટાવરની ઊંચાઈ …….. મી છે.
A. 250√3
B. 500√3
C. 500/√3
D. 250
( 9 ) સમથળ જમીન પર એક ટાવર ઊભો છે. જ્યારે સૂર્યનો ઉત્સેધકોણ 30° હોય ત્યારે અને જ્યારે સૂર્યનો ઉત્સેધકોણ 60° હોય ત્યારે તેના પડછાયાની લંબાઈમાં 45 મીનો તફાવત જોવા મળે છે, તો ટાવરની ઊંચાઈ ……… મી હોય.
A. 45√3/2
B. 45√3
C. 45√2
D. 45/√3
(10) એક ટાવરના તળિયાથી 30 મી દૂર આવેલ એક બિંદુથી ટાવરની ટોચનો ઉત્સેધકોણ 30° છે, તો તે જ ટાવરના તળિયાથી 10 મી દૂર આવેલા બિંદુથી ટાવરની ટોચનો ઉત્સેધકોણ …….. થાય.
A. 10°
B. 45°
C. 60°
D. 15°
3. નીચેના દરેક પ્રશ્નનો એક શબ્દ, સંખ્યા અથવા વાક્યમાં જવાબ લખો :
( 1 ) એક ટાવરની ઊંચાઈ 10 મી છે. જ્યારે સૂર્યનો ઉત્સેધકોણ 45° હોય ત્યારે ટાવરના પડછાયાની લંબાઈ કેટલી હોય?
( 2 ) 1.5 મી ઊંચાઈની એક વ્યક્તિ 30 મી ઊંચાઈના ટાવરના તળિયાથી 28.5 મી દૂરથી ટાવરની ટોચનું નિરીક્ષણ કરે, તો તેને ટાવરની ટોચના ઉત્સેધકોણનું માપ કેટલું મળે?
( 3 ) 1.7 મી ઊંચાઈની એક વ્યક્તિ એક ટાવરના તળિયાથી 20√3 મી દૂર સ્થિત છે. તે વ્યક્તિની આંખોથી જોતાં ટાવરની ટોચનો ઉત્સેધકોણ 30॰ જણાય છે. ટાવરની ઊંચાઈ શોધો.
( 4 ) એક થાંભલાની ઊંચાઈમાં વધ-ઘટ કરી શકાય છે. જમીન પરનાં એક બિંદુથી તે થાંભલાની ટોચનો ઉત્સેધકોણ કોઈ એક પરિસ્થિતિમાં 30° છે. હવે, જો થાંભલાની ઊંચાઈ ત્રણ ગણી કરવામાં આવે, તો તે જ બિંદુએથી થાંભલાની ટોચનો ઉત્સેધકોણ કેટલો થાય?
( 5 ) બે ટાવરની ઊંચાઈ અનુક્રમે x અને y છે. તે ટાવરના તળિયાને જોડતા રેખાખંડના મધ્યબિંદુ પરથી નિરીક્ષણ કરતાં તે ટાવરોની ટોચના ઉત્સેધકોણ અનુક્રમે 30° અને 60° મળે છે. ગુણોત્તર x : y શોધો.
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) એક દીવાદાંડીની ટોચ પરથી જોતાં દરિયામાં રહેલ બે વહાણ P અને Qના અવસેધકોણ અનુક્રમે 15° અને 30° છે, તો વહાણ P દીવાદાંડીની વધુ નજીક છે.
( 2 ) જ્યારે સૂર્યનો ઉત્સેધકોણ 45° હોય, ત્યારે એક ટાવરની ઊંચાઈ તથા તેના પડછાયાની લંબાઈ સમાન હોય.
( 3 ) એક કાટકોણ ત્રિકોણમાં એક લઘુકોણનું માપ 30° છે, તો તે ખૂણાની સામેની બાજુનું માપ કર્ણના માપથી અડધું હોય.
( 4 ) 10 મી લાંબી નિસરણી દીવાલ પર ગોઠવતાં દીવાલ પર 5 મી ઊંચાઈએ પહોંચે છે. આથી, નિસરણી દીવાલ સાથે 30°નો ખૂણો બનાવે છે.
( 5 ) જમીન સાથે 30ના ખૂણે ઢોળાવવાળા રસ્તા પર 20 મી ચાલતાં જમીનથી 10મી ઊંચાઈ પર પહોંચાય.

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here