Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 10 વર્તુળ
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 10 વર્તુળ
સ્વાધ્યાય – 10.1
1. ખાલી જગ્યા પૂરો :
( 1 ) વર્તુળનું કેન્દ્ર વર્તુળના………ના ભાગમાં હોય છે. (બહાર / અંદર)
(ii) જે બિંદુનું વર્તુળના કેન્દ્રથી અંતર તેની ત્રિજ્યા કરતાં વધારે હોય, તે બિંદુ વર્તુળના ……ના ભાગમાં આવેલું છે. (બહાર / અંદર)
(iii) વર્તુળની મોટામાં મોટી જીવા એ વર્તુળનો ……… છે.
(iv) જ્યારે ચાપનાં અંત્યબિંદુઓ એ વ્યાસનાં અંત્યબિંદુઓ હોય, તો તે ચાપ ……… છે.
(v) વર્તુળનો વૃત્તખંડ એ વર્તુળના ચાપ અને ……… વચ્ચેનો પ્રદેશ છે.
(vi) સમતલમાં આવેલું વર્તુળ, તે સમતલના ……. ભાગ કરે છે.
જવાબ : ( i ) અંદર (ii) બહાર (iii) વ્યાસ (iv) અર્ધવર્તુળ (v) જીવા (vi) ત્રણ
2. નીચેનાં વિધાનો સત્ય છે કે અસત્ય છે તે લખો. તમારા જવાબનાં કારણ આપો :
(i) કેન્દ્રને વર્તુળના કોઈ પણ બિંદુ સાથે જોડતો રેખાખંડ એ વર્તુળની ત્રિજ્યા છે.
આપેલ વિધાન સત્ય છે, કારણ કે ત્રિજ્યાની વ્યાખ્યા મુજબ ત્રિજ્યા એ કેન્દ્રને વર્તુળના કોઈ પણ બિંદુ સાથે જોડતો રેખાખંડ છે.
(ii) વર્તુળની સમાન જીવાઓની સંખ્યા સાન્ત હોય છે.
આપેલ વિધાન અસત્ય છે, કારણ કે વર્તુળમાં સમાન જીવાઓની સંખ્યા અસંખ્ય હોય છે. ઘ. ત., વર્તુળના વ્યાસ એ સમાન જીવાઓ છે અને વર્તુળમાં અસંખ્ય વ્યાસ હોય છે.
(iii) જો વર્તુળને ત્રણ સમાન ચાપમાં વિભાજિત કરવામાં આવે, તો તે પ્રત્યેક ગુરુચાપ છે.
આપેલ વિધાન અસત્ય છે, કારણ કે વર્તુળને ત્રણ સમાન ચાપમાં વિભાજિત કરતાં મળતાં ત્રણેય ચાપ લઘુચાપ હોય છે.
(iv) વર્તુળની જીવા કે જેની લંબાઈ ત્રિજ્યાથી બમણી છે, તેને વર્તુળનો વ્યાસ કહે છે.
આપેલ વિધાન સત્ય છે, કારણ કે જેની લંબાઈ ત્રિજ્યાથી બમણી છે તેવી જીવા વર્તુળના કેન્દ્રમાંથી પસાર થાય અને કેન્દ્રમાંથી પસાર થતી જીવાને વ્યાસ કહે છે.
(v) જીવા અને તેને સંગત ચાપની વચ્ચેના પ્રદેશને વૃત્તાંશ કહે છે.
આપેલ વિધાન અસત્ય છે, કારણ કે જીવા અને તેને સંગત ચાપની વચ્ચેના પ્રદેશને વૃત્તખંડ કહે છે.
(vi) વર્તુળ એ સમતલીય આકૃતિ છે.
આપેલ વિધાન સત્ય છે, કારણ કે વર્તુળ એ સમતલનાં નિશ્ચિત બિંદુથી નિશ્ચિત અંતરે આવેલાં તે સમતલનાં બિંદુઓનો સમૂહ છે.
સ્વાધ્યાય – 10.2
1. યાદ કરો કે જો બે વર્તુળોની ત્રિજ્યાઓ સમાન હોય, તો તે બે વર્તુળો સમાન છે. સાબિત કરો કે, સમાન વર્તુળોની સમાન જીવાઓ તેમના કેન્દ્ર આગળ સમાન ખૂણા આંતરે છે.
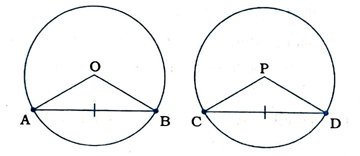
O કેન્દ્ર અને P કેન્દ્ર ધરાવતાં બે વર્તુળો સમાન છે. ઉપરાંત, O કેન્દ્રવાળા વર્તુળની જીવા AB અને P કેન્દ્રવાળા વર્તુળની જીવા CD પણ સમાન છે.
Δ OAB અને Δ PCDમાં,
OA = PC અને OB = PD (સમાન વર્તુળોની ત્રિજ્યાઓ)
ઉપરાંત, AB = CD (પક્ષ)
∴ બાબાબા મુજબ, Δ OAB ≅ Δ PCD
∴ ∠AOB = ∠CPD
આમ, સમાન વર્તુળોની સમાન જીવાઓ તેમના કેન્દ્ર આગળ સમાન ખૂણા આંતરે છે.
2. સાબિત કરો કે એકરૂપ વર્તુળોની જીવાઓ તેમના કેન્દ્ર આગળ સમાન ખૂણા આંતરે, તો તે જીવાઓ સમાન છે.
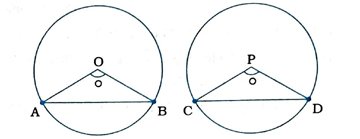
O કેન્દ્ર અને P કેન્દ્ર ધરાવતા બે વર્તુળો સમાન છે. ઉપરાંત, O કેન્દ્રવાળા વર્તુળમાં જીવા AB એ કેન્દ્ર આગળ આંતરેલ ∠AOB અને P કેન્દ્રવાળા વર્તુળમાં જીવા CD એ કેન્દ્ર આગળ આંતરેલ ∠CPD પણ સમાન છે.
Δ OAB અને Δ PCDમાં,
OA = PC અને OB = PD (સમાન વર્તુળોની ત્રિજ્યાઓ)
ઉપરાંત, ∠AOB = ∠CPD (પક્ષ)
∴ બાખૂબા મુજબ, Δ OAB ≅ Δ PCD
∴ AB = CD
આમ, એકરૂપ (સમાન) વર્તુળોની જીવાઓ તેમના કેન્દ્ર આગળ સમાન ખૂણા આંતરે, તો તે જીવાઓ સમાન છે.
સ્વાધ્યાય – 10.3
1. વર્તુળોની જુદી જુદી જોડીઓ દોરો. પ્રત્યેક જોડીમાં કેટલાં બિંદુઓ સામાન્ય છે? સામાન્ય બિંદુઓની મહત્તમ સંખ્યા કેટલી?
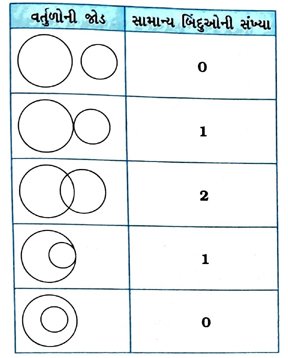
આમ, વર્તુળોની જોડમાં સામાન્ય બિંદુની મહત્તમ સંખ્યા 2 છે.
2. ધારો કે, તમને એક વર્તુળ આપવામાં આવ્યું છે. તેનું કેન્દ્ર શોધવાની રચના કરો.
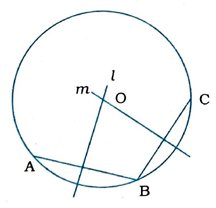
(1) આપેલ વર્તુળમાં બે જીવાઓ AB અને BC દોરો, જેમનું એક અંત્યબિંદુ સમાન હોય.
(2) ABનો લંબદ્વિભાજક l અને BCનો લંબદ્વિભાજક m દોરો.
(3) l અને mના છેદબિંદુને O નામ આપો.
(4) O એ આપેલ વર્તુળનું કેન્દ્ર છે.
નોંધ : અહીં, સામાન્ય અંત્યબિંદુ ન હોય તેવી બે જીવાઓ પણ દોરી શકાય.
3. જો બે વર્તુળો એકબીજાંને બે બિંદુમાં છેદે તો સાબિત કરો કે તેમના કેન્દ્ર, સામાન્ય જીવાના લંબદ્વિભાજક પર છે.
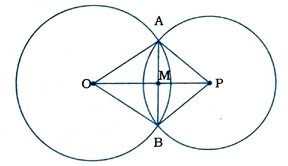
અહીં, O કેન્દ્રિત વર્તુળ અને P કેન્દ્રિત વર્તુળ બે બિંદુઓ A અને Bમાં છેદે છે.
AB અને OP એકબીજાને M બિંદુમાં છેદે છે.
Δ OAP અને Δ OBPમાં
OA = OB (એક જ વર્તુળની ત્રિજ્યાઓ)
PA = PB (એક જ વર્તુળની ત્રિજ્યાઓ)
OP = OP (સામાન્ય બાજુઓ)
∴ બાબાબા મુજબ, Δ OAP ≅ Δ OBP
∴ ∠AOP = ∠BOP
∴ ∠AOM = ∠BOM
Δ AOM અને Δ BOMમાં,
AO = BO (એક જ વર્તુળની ત્રિજ્યાઓ)
∠AOM = ∠BOM
OM = OM (સામાન્ય બાજુ)
∴ બાખૂબા મુજબ, Δ AOM ≅ Δ BOM
∴ AM = BM અને ∠AMO = ∠BMO
પરંતુ, ∠AMO + ∠BMO = 180° (રેખિક જોડ)
આમ, રેખા OM એ ABનો લંબદ્વિભાજક છે.
આથી રેખા OP એ ABનો લંબદ્વિભાજક છે.
આમ, બે બિંદુમાં છેદતાં વર્તુળોનાં કેન્દ્રો O અને Pતેમની સામાન્ય જીવા ABના લંબદ્વિભાજક પર છે.
સ્વાધ્યાય – 10.4
1. 5 સેમી અને 3 સેમી ત્રિજ્યાવાળાં બે વર્તુળો બે બિંદુમાં છેદે છે અને તેમના કેન્દ્ર વચ્ચેનું અંતર 4 સેમી છે. સામાન્ય જીવાની લંબાઈ શોધો.

O કેન્દ્ર અને 5 સેમી ત્રિજ્યાવાળું વર્તુળ P કેન્દ્ર અને 3 સેમી ત્રિજ્યાવાળા વર્તુળને બે બિંદુઓ A અને Bમાં છેદે છે. આથી AB તેઓની સામાન્ય જીવા છે.
વળી, OP = 4 સેમી આપેલ છે.
OA = 5 સેમી અને PA = 3 સેમી થાય.
Δ OAPમાં, OA2 = 52 = 25 અને
OP2 + AP2 = 42 + 32 = 16 + 9 = 25
આમ, Δ OAPમાં OA2 = OP2 + AP2
∴ Δ OAP કાટકોણ ત્રિકોણ છે, જેમાં OA કર્ણ અને ∠OPA કાટખૂણો છે.
આમ, O કેન્દ્રિત વર્તુળમાં OP એ જીવા ABને લંબ છે.
∴ OP એ ABને દુભાગે છે.
∴ AB = 2PA = 2 × 3 = 6 સેમી
આમ, આપેલ વર્તુળોની સામાન્ય જીવાની લંબાઈ 6 સેમી થાય.
2. જો વર્તુળની બે સમાન જીવાઓ વર્તુળની અંદર છેડે, તો એક જીવાના કપાતા ભાગ અને બીજી જીવાના અનુરૂપ ભાગ સમાન છે, તેમ સાબિત કરો.
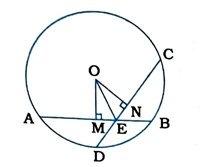
O કેન્દ્રિત વર્તુળની સમાન જીવાઓ AB અને CD પરસ્પર E બિંદુમાં છેદે છે.
OM ⊥ AB તથા ON ⊥ CD દોરો.
∴ AM = BM = 1/2 AB અને CN = DN = 1/2 CD થાય.
પરંતુ AB = CD છે.
∴ AM = BM = CN = DN ….. (1)
જીવાઓ AB અને CD સમાન હોવાથી કેન્દ્રથી સમાન અંતરે છે.
∴ OM = ON
Δ OME અને Δ ONEમાં,
∠OME = ∠ONE (કાટખૂણા)
OE = OE (સામાન્ય બાજુ)
OM = ON
∴ કાકબા મુજબ, Δ OME ≅ Δ ONE
∴ ME = EN …… (2)
(1) અને (2) પરથી,
AM + ME = CN + NE
∴ AE = CE
તે જ રીતે, BM – ME = DN – NE
∴ BE = DE
આમ, વર્તુળની બે સમાન જીવાઓ AB અને CD વર્તુળની અંદર છેદતી હોવાથી તેમના અનુરૂપ ભાગો AE અને CE તથા BE અને DE સમાન છે.
3. જો વર્તુળની બે સમાન જીવાઓ વર્તુળની અંદર છેદે, તો સાબિત કરો કે છેદબિંદુને કેન્દ્ર સાથે જોડતી રેખા જીવાઓ સાથે સમાન ખૂણા બનાવે છે.
દાખલા 3માં આપેલ માહિતી દાખલા 2ની માહિતીને સમાન છે. આથી આપણે દાખલા 2ની સાબિતીનો યોગ્ય સ્થાન સુધી ઉપયોગ કરીશું.
દાખલા 2માં આપણે સાબિત કર્યું કે,
Δ ΟΜΕ ≅ Δ ΟΝΕ
∴ ∠OEM = ∠OEN
∴ ∠OEA = ∠OEC
આમ, છેદબિંદુને કેન્દ્ર સાથે જોડતી રેખા જીવાઓ સાથે સમાન ખૂણા બનાવે છે.
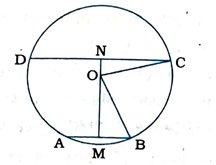
4. જો O કેન્દ્રવાળા બે સમકેન્દ્રી (concentric) વર્તુળો(સમાન કેન્દ્રવાળાં વર્તુળો)ને એક રેખા અનુક્રમે A, B, C અને Dમાં છેદે, તો સાબિત કરો કે AB = CD. (જુઓ આકૃતિ)

કેન્દ્ર Oમાંથી રેખા AD પર લંબ OM દોરો.
મોટા વર્તુળની જીવા AD પર કેન્દ્ર Oમાંથી લંબ OM દોરેલ છે. માટે, M એ ADનું મધ્યબિંદુ છે.
∴ MA = MD ….. (1)
નાના વર્તુળની જીવા BC પર કેન્દ્ર Oમાંથી લંબ OM દોરેલ છે. માટે, M એ BCનું મધ્યબિંદુ છે.
∴ MB = MC ….. (2)
(1)માંથી (2) બાદ કરતાં,
MA – MB = MD – MC
∴ AB = CD
5. એક વિહારસ્થાનમાં 5 મી ત્રિજ્યાવાળા દોરેલા વર્તુળ પર રમત રમવા માટે ત્રણ છોકરીઓ રેશ્મા, સલમા અને મનદીપ ઊભાં છે. રેશ્મા દડાને સલમા તરફ ફેંકે છે. સલમા મનદીપ તરફ અને મનદીપ રેશ્મા તરફ દડો ફેંકે છે. જો રેશ્મા અને સલમા વચ્ચેનું તથા સલમા અને મનદીપ વચ્ચેનું દરેક અંતર 6 મીટર હોય, તો રેશ્મા અને મનદીપ વચ્ચેનું અંતર કેટલું હશે?
અહીં દર્શાવેલ વર્તુળ પર R, S અને M અનુક્રમે રેશ્મા, સલમા અને મનદીપનાં સ્થાન દર્શાવે છે.
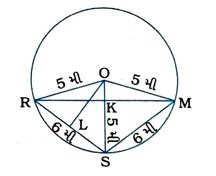
આથી OR = OM = OS = 5 મીટર (વર્તુળની ત્રિજ્યા)
તથા RS = SM = 6 મીટર
ચતુષ્કોણ ORSMમાં OR = OM = 5 મી અને
RS = SM = 6 મી
માટે, ચતુષ્કોણ ORSM પતંગાકાર છે.
આથી તેનો વિકર્ણ OS એ વિકર્ણ RMને કાટખૂણે દુભાગે છે.
∴ ∠RKO = 90° … (1)
વર્તુળના કેન્દ્ર Oમાંથી જીવા RM ૫૨ લંબ OK છે. માટે, K એ RMનું મધ્યબિંદુ છે.
∴ RM = 2RK
કેન્દ્ર Oમાંથી જીવા RS પર લંબ OL દોરો.

6. એક વસાહતમાં 20 મીટર ત્રિજ્યાવાળું એક વર્તુળાકાર વિહારસ્થાન આવેલું છે. ત્રણ છોકરાઓ અંકુર, સૈયદ અને ડેવિડ દરેક પોતાના હાથમાં રમકડાનો ટેલિફોન એકબીજા સાથે વાત કરવા માટે રાખીને વર્તુળની સીમા પર સરખા અંતરે બેઠા છે. દરેકના ટેલિફોનની દોરીની લંબાઈ શોધો.

O કેન્દ્રિત વર્તુળ એ વિહારસ્થાન દર્શાવે છે તથા A, S અને D અનુક્રમે અંકુર, સૈયદ અને ડેવિડના સ્થાન દર્શાવે છે. અંકુર, સૈયદ અને ડેવિડ સરખા અંતરે બેઠા હોવાથી A ASD સમબાજુ ત્રિકોણ છે.
SDના મધ્યબિંદુ Mમાંથી તેનો લંબદ્વિભાજક દોરતાં તે O અને A બંનેમાંથી પસાર થાય.
ધારો કે, SM = x મી
∴ SD = 2SM = 2x મી

સ્વાધ્યાય – 10.5
1. આપેલ આકૃતિમાં O કેન્દ્રવાળા વર્તુળ પર બિંદુઓ A, B અને C એવી રીતે આવેલાં છે કે જેથી ∠BOC = 30° અને ∠AOB = 60° થાય. જો ચાપ ABC સિવાયના વર્તુળ પર બિંદુ D હોય, તો ∠ADC શોધો.

2. એક વર્તુળની જીવા અને તેની ત્રિજ્યા સમાન છે. આ જીવાએ લઘુચાપ પરના બિંદુ આગળ અને ગુરુચાપ પરના બિંદુ આગળ આંતરેલા ખૂણા શોધો.
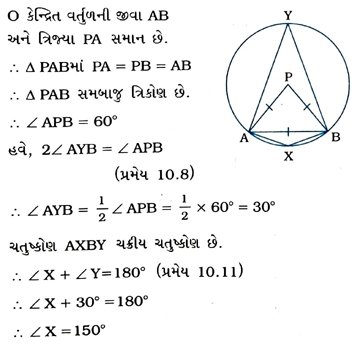
આમ, લઘુચાપ પરના બિંદુ X આગળ આંતરેલો ખૂણો 150° છે અને ગુરુચાપ પરના બિંદુ Y આગળ અતિરેલો ખૂણો 30° છે.
3. આપેલ આકૃતિમાં ∠PQR = 100°; જ્યાં P, Q અને R એ O કેન્દ્રવાળા વર્તુળ પરનાં બિંદુઓ છે. ∠OPR શોધો.

અહીં વિપરીતકોણ ∠POR = 2 × ∠PQR (પ્રમેય 10,8)
∴ વિપરીતકોણ ∠POR = 2 × 100° = 200°
હવે, ∠POR + વિપરીતકોણ ∠POR = 360°
∴ ∠POR + 200° = 360°
∴ ∠POR = 160°
Δ OPRમાં OP = OR (ત્રિજ્યાઓ)
∴ ∠OPR = ∠ORP
Δ OPRમાં ∠OPR + ∠ORP + ∠POR = 180°
∴ ∠OPR + ∠OPR + 160 = 180°
∴ 2∠ OPR = 20°
∴ ∠OPR = 10°
4. આપેલ આકૃતિમાં ∠ABC = 69°, ∠ACB = 31° છે, ∠BDC શોધો.

Δ ABCમાં, ∠ABC + ∠ACB + ∠BAC = 180°
∴ 69° + 31° + ∠BAC = 180°
∴ 100° + ∠BAC = 180°
∴ ∠BAC = 80°
હવે, ∠BDC = ∠BAC (પ્રમેય 10.9)
∴ ∠BDC = 80°
5. આપેલ આકૃતિમાં વર્તુળ પર ચાર બિંદુઓ A, B, C અને D આવેલાં છે. AC અને BD એ E બિંદુએ એવી રીતે છેદે છે કે જેથી ∠BEC = 130° અને ∠ECD = 20°. / BAC શોધો.

Δ CDEમાં ∠BEC બહિષ્કોણ છે.
∴ ∠BEC = ∠ECD + ∠EDC
∴ 130° = 20° + ∠BDC
∴ ∠BDC = 110°
હવે, ∠BAC = ∠BDC (પ્રમેય 10.9) .
∴ ∠BAC = 110°
6. ચક્રીય ચતુષ્કોણ ABCDના વિકર્ણો E બિંદુએ છેદે છે. જો ∠DBC = 70°, ∠BAC = 30°, તો ∠BCD શોધો અને જો AB = BC, તો ∠ECD શોધો.

∠DAC = ∠DBC (પ્રમેય 10.9)
∴ ∠DAC = 70°
∠BAD = ∠BAC + ∠DAC (આસન્નકોણ)
∴ ∠BAD = 30° + 70°
∴ ∠BAD = 100°
ચક્રીય ચતુષ્કોણ ABCDમાં,
∠BAD + ∠BCD = 180° (પ્રમેય 10.11)
∴ 100° + ∠BCD = 180°
∴ ∠BCD = 80°
Δ ABCમાં AB = BC હોય, તો ∠BAC = ∠BCA
∴ 30° = ∠BCA
∴ ∠BCA = 30°
∠BCD = ∠BCA + ∠ACD (આસન્નકોણ)
∴ 80° = 30° + ∠ACD
∴ ∠ACD = 50°
∴ ∠ECD = 50°
7. જો ચક્રીય ચતુષ્કોણના વિકર્ણી એ ચતુષ્કોણનાં શિરોબિંદુઓમાંથી પસાર થતા વર્તુળના વ્યાસ હોય, તો સાબિત કરો કે, તે લંબચોરસ છે.

ચક્રીય ચતુષ્કોણ ABCDનાં બિંદુઓ O કેન્દ્રિત વર્તુળ પ૨ આવેલાં છે તથા AC અને BD તે વર્તુળના વ્યાસ છે.
AC વ્યાસ હોવાથી ∠ABC = ∠ADC = 90° (અર્ધવર્તુળમાંનો ખૂણો)
BD વ્યાસ હોવાથી ∠BCD = ∠BAD = 90° (અર્ધવર્તુળમાંનો ખૂણો)
આમ, ચતુષ્કોણ ABCDના ચારેય ખૂણા ∠BAD, ∠ABC, ∠BCD અને ∠ADC કાટખૂણા છે.
∴ ચતુષ્કોણ ABCD લંબચોરસ છે.
8. જો સમલંબ ચતુષ્કોણની સમાંતર ન હોય તેવી બાજુઓ સમાન હોય, તો સાબિત કરો કે તે ચક્રીય છે.

સમલંબ ચતુષ્કોણ ABCDમાં AB || CD અને AD = BC.
A અને Bમાંથી CD પર અનુક્રમે લંબ AM તથા BN દોરો.
Δ AMD અને Δ BNCમાં
∠AMD = ∠BNC (કાટખૂણા)
કર્ણ AD = કર્ણ BC (પક્ષ)
AM = BN (બે સમાંતર રેખાઓ વચ્ચેનું અંતર)
∴ કાકબા મુજબ, Δ AMD ≅ Δ BNC
∴ ∠ADM = ∠BCN (CPCT)
∴ ∠ADC = ∠BCD
હવે, AB || CD અને AD તેમની છેદિકા છે.
∴ ∠BAD + ∠ADC = 180° (છેદિકાની એક તરફના અંતઃકોણ)
∴ ∠BAD + ∠BCD = 180°
આમ, ચતુષ્કોણ ABCDમાં ∠A + ∠C = 180°
માટે, ચતુષ્કોણ ABCD ચક્રીય ચતુષ્કોણ છે.
9. બે વર્તુળો એકબીજાને બે બિંદુઓ B અને Cમાં છેદે છે. Bમાંથી પસાર થતાં બે રેખાખંડ ABD અને PBQ વર્તુળોને અનુક્રમે A, D અને P, Qમાં છેદે તે રીતે દોરેલાં છે. (જુઓ આકૃતિ) સાબિત કરો કે, ∠ACP = ∠QCD.

10. જો ત્રિકોણની બે બાજુઓ વ્યાસ થાય તેવી રીતે વર્તુળો દોરેલાં હોય, તો સાબિત કરો કે, આ વર્તુળોનું એક છેદબિંદુ, ત્રિકોણની ત્રીજી બાજુ પર આવેલું છે.

Δ ABCની બાજુઓ AB અને AC વ્યાસ થાય તે રીતે વર્તુળો દોરેલ છે જે એકબીજાને A અને P બિંદુમાં છેદે છે.
સામાન્ય જીવા AP દોરો.
AB વ્યાસ હોવાથી ∠APB અર્ધવર્તુળે આંતરેલો ખૂણો છે.
∴ ∠APB = 90°
AC વ્યાસ હોવાથી ∠APC અર્ધવર્તુળે આંતરેલો ખૂણો છે.
∴ ∠APC = 90°
આથી ∠APB + ∠APC = 90° + 90° = 180°
∠APB અને ∠APC સામાન્ય ભુજ AP ધરાવતા આસજ્નકોણ છે અને તેમનો સરવાળો 180° છે.
∴ ∠APB અને ∠APC રેખિક જોડના ખૂણા છે.
∴ બિંદુ P એ Δ ABCની ત્રીજી બાજુ BC પર આવેલું છે.
11. કર્ણ AC હોય તેવા બે કાટકોણ ત્રિકોણ ABC અને ADC છે. સાબિત કરો કે, ∠CAD = ∠CBD.
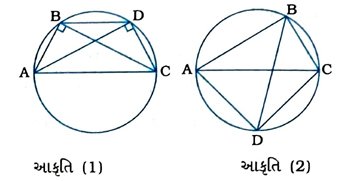
આકૃતિ (1)માં રેખાખંડ AC રેખાની એક જ તરફ આવેલાં બિંદુઓ B અને D આગળ સમાન ખૂણા આંતરે છે. આથી પ્રમેય 10.10 મુજબ ચારેય બિંદુઓ એક જ વર્તુળ પર આવેલાં છે.
હવે, ∠CAD અને ∠CBD એક જ વૃત્તખંડમાં આવેલાં ખૂણા છે.
∴ ∠CAD = ∠CBD (પ્રમેય 10.9)
આકૃતિ (2)માં ચતુષ્કોણ ABCDમાં ∠B = ∠D = 90°
એટલે કે, ∠B + ∠D = 180°
માટે, ABCD ચક્રીય ચતુષ્કોણ છે.
અહીં, ∠CAD અને ∠CBD એક જ વૃત્તખંડમાં આવેલાં ખૂણા છે.
∴ ∠CAD = ∠CBD (પ્રમેય 10.9)
12. સાબિત કરો કે, ચક્રીય સમાંતરબાજુ ચતુષ્કોણ એ લંબચોરસ છે.
ચતુષ્કોણ ABCD ચક્રીય સમાંતરબાજુ ચતુષ્કોણ છે.
ABCD ચક્રીય ચતુષ્કોણ છે.
∴ ∠A + ∠C = 180°
અને ∠B + ∠D = 180° ….. (1)
ABCD સમાંતરબાજુ ચતુષ્કોણ છે.
∴ ∠A = ∠C અને ∠B = ∠D ….. (2)
(1) અને (2) પરથી,
∠A = ∠B = ∠C = ∠D = 90°
આમ, ચતુષ્કોણ ABCDના ચારેય ખૂણા કાટખૂણા છે.
માટે, ABCD લંબચોરસ છે.
આમ, ચક્રીય સમાંતરબાજુ ચતુષ્કોણ એ લંબચોરસ છે.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરોઃ (ફક્ત અંતિમ જવાબ)
( 1 ) વર્તુળનું કેન્દ્ર વર્તુળના દરેક બિંદુથી …….. અંતરે હોય છે.
( 2 ) વર્તુળની પૂર્ણ લંબાઈને વર્તુળનો ……… કહે છે.
( 3 ) વર્તુળની કોઈ પણ ત્રિજ્યાનું માપ તેના વ્યાસ કરતાં ……… હોય.
( 4 ) વર્તુળના ત્રણ ભિન્ન બિંદુઓ કદી પણ ……… ન હોય.
( 5 ) વર્તુળનાં બે ભિન્ન બિંદુઓને જોડતા રેખાખંડને વર્તુળની …….. કહે છે.
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) AB અને CD એ P કેન્દ્રિત વર્તુળની સમાન જીવાઓ છે. જો ∠APB = 85° હોય, તો ∠CPD શોધો.
( 2 ) P કેન્દ્રિત વર્તુળની સૌથી મોટી જીવા ABનું માપ 15 સેમી હોય, તો વર્તુળની ત્રિજ્યા શોધો.
( 3 ) P કેન્દ્રિત વર્તુળની AB જીવા છે અને C એ ગુરુચાપનું બિંદુ છે. જો ∠ACB = 42° હોય, તો ∠APB શોધો.
( 4 ) ચક્રીય ચતુષ્કોણ ABCDમાં ∠A: ∠C =4 : 5 હોય, તો ∠C શોધો.
( 5 ) ચક્રીય ચતુષ્કોણ ABCDની બાજુ ABને B તરફ M સુધી લંબાવેલ છે. જો ∠CBM = 100° હોય, તો ∠ADC શોધો.
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) P કેન્દ્રિત વર્તુળની જીવા ABની લંબાઈ 16 સેમી છે અને તેનું કેન્દ્રથી અંતર 15 સેમી છે, તો વર્તુળની ત્રિજ્યા ……. સેમી હોય.
A. 20
B. 22
C. 14
D. 17
( 2 ) O કેન્દ્રિત વર્તુળમાં AB જીવા છે. જો ∠AOB = 60° હોય, તો ΔOAB ……. ત્રિકોણ છે.
A. સમઢિભુજ
B. સમભુજ
C. કાટકોણ
D. વિષમભુજ
( 3 ) AB વ્યાસવાળા વર્તુળ પર બિંદુ P છે. જો ΔPABમાં ∠A = 48° હોય, તો ∠B = ……..
A. 48°
B. 96°
C. 42°
D. 24°
( 4 ) P કેન્દ્રિત વર્તુળની જીવાઓ AB અને CD કાટખૂણે બિંદુ Mમાં છેદે છે. જો ∠MAD = 55° હોય, તો ∠ABC = ……..
A. 35°
B. 55°
C. 110°
D. 45°
( 5 ) ચક્રીય ચતુષ્કોણ ABCDમાં ∠A : ∠B : ∠C : ∠D = ……… શક્ય છે.
A. 2:3: 2:3
B.4:5:6:3
C. 3: 4: 6:5
D4:6:3:5
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) વર્તુળની જીવાના તમામ બિંદુઓ વર્તુળ પર હોય.
( 2 ) ચક્રીય ચતુષ્કોણના પાસપાસેના ખૂણા પૂરક હોય છે.
( 3 ) એક જ વર્તુળની બે અસમાન જીવાઓ પૈકી નાની જીવા કેન્દ્રથી નજીક હોય.
( 4 ) વર્તુળમાં અંતર્ગત સમાંતરબાજુ ચતુષ્કોણ સમબાજુ ચતુષ્કોણ હોય.
( 5 ) એક જ વર્તુળની બે જીવાઓ પરસ્પર દુભાગે, તો તે બંને વ્યાસ હોય.
જવાબો
1. ( 1 ) સમાન ( 2 ) પરિઘ ( 3 ) અડધું ( 4 ) સમરેખ ( 5 ) જીવા
2. ( 1 ) 85° ( 2 ) 7.5 સેમી ( 3 ) 84° ( 4 ) 100° (5) 100°
3. ( 1 ) 17 ( 2 ) સમભુજ ( 3 ) 42° ( 4 ) 35° ( 5 ) 3:4:6:5
4. ( 1 ) ખોટું ( 2 ) ખોટું ( 3 ) ખોટું ( 4 ) ખોટું ( 5 ) ખરું
સ્વાધ્યાય – 10.6 (વૈકલ્પિક)*
1. સાબિત કરો કે, બે છેદતાં વર્તુળોના કેન્દ્રને જોડતો રેખાખંડ વર્તુળોનાં બે છેદબિંદુ આગળ સમાન ખૂણા આંતરે છે.
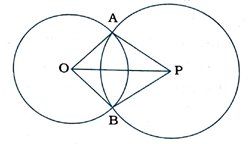
O કેન્દ્રિત અને P કેન્દ્રિત વર્તુળો એકબીજાને બિંદુઓ A અને B આગળ છેદે છે.
Δ OAP અને Δ OBPમાં,
OA = OB (O કેન્દ્રિત વર્તુળની ત્રિજ્યાઓ)
PA = PB (P કેન્દ્રિત વર્તુળની ત્રિજ્યાઓ)
OP = OP (સામાન્ય બાજુ)
∴ બાબાબા મુજબ, Δ OAP = Δ OBP
∴ ∠OAP = ∠OBP (CPCT)
આમ, OP એ બિંદુ A અને B આગળ સમાન ખૂણા આંતરે છે. આમ, બે છેદતાં વર્તુળોના કેન્દ્રને જોડતો રેખાખંડ વર્તુળોનાં બે છેદબિંદુ આગળ સમાન ખૂણા આંતરે છે.
2. વર્તુળની 5 સેમી અને 11 સેમી લંબાઈની બે જીવાઓ અનુક્રમે AB અને CD એકબીજીને સમાંતર છે અને કેન્દ્રની વિરુદ્ધ બાજુએ આવેલી છે. AB અને CD વચ્ચેનું અંતર 6 સેમી હોય, તો વર્તુળની ત્રિજ્યા શોધો.


3. વર્તુળની બે સમાંતર જીવાઓની લંબાઈ 6 સેમી અને 8 સેમી છે. નાની જીવા કેન્દ્રથી 4 સેમી દૂર હોય, તો કેન્દ્રથી બીજી જીવાનું અંતર કેટલું હશે?

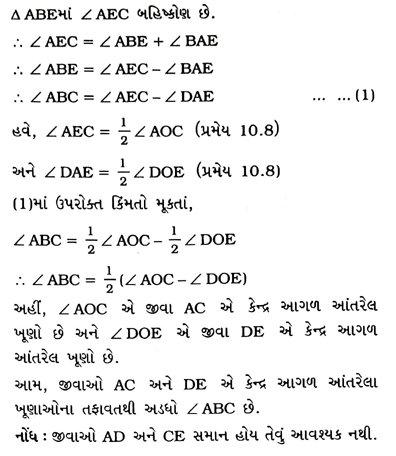
4. ધારો કે ખૂણા ABCનું શિરોબિંદુ વર્તુળની બહારના ભાગમાં આવેલું છે અને ખૂણાની બાજુઓ સમાન જીવાઓ AD અને CE બને તે રીતે વર્તુળને છેદે છે. સાબિત કરો કે, જીવાઓ AC અને DE એ કેન્દ્ર આગળ આંતરેલા ખૂણાઓના તફાવતથી અડધો ∠ABC છે.

5. સાબિત કરો કે સમબાજુ ચતુષ્કોણની કોઈ પણ બાજુને વ્યાસ તરીકે લઈ દોરેલું વર્તુળ ચતુષ્કોણના વિકર્ણોના છેદબિંદુમાંથી પસાર થાય છે.
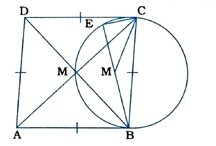
ABCD સમબાજુ ચતુષ્કોણ છે જેના વિકર્ણો AC અને BD બિંદુ Mમાં છેદે છે.
∴ ∠BMC કાટખૂણો છે.
BCને વ્યાસ લઈને એક વર્તુળ છે.
M માટે ત્રણ શક્યતાઓ છે :
( 1 ) M વર્તુળના અંદરના ભાગમાં છે.
( 2 ) M વર્તુળના બહારના ભાગમાં છે.
( 3 ) M વર્તુળ પર છે.
શક્યતા (1) મુજબ, જો M વર્તુળના અંદરના ભાગમાં હોય તો BMને લંબાવતા તે વર્તુળને Eમાં છેદે. ∠BEC અર્ધવર્તુળનો ખૂણો હોવાથી કાટખૂણો થાય. એટલે કે ∠MEC = 90° અને Δ MECમાં ∠BMC બહિષ્કોણ હોવાથી ∠BMC > 90° થાય. આ પરિસ્થિતિમાં ∠BMC ગુરુકોણ થાય જે શક્ય નથી. તે જ રીતે શક્યતા (2) મુજબ, જો M વર્તુળના બહારના ભાગમાં હોય, તો ∠BMC લઘુકોણ થાય જે શક્ય નથી.
આથી શક્યતા (3) જ સાચી છે. એટલે કે M એ વર્તુળ પર છે. આમ, સમબાજુ ચતુષ્કોણની કોઈ પણ બાજુને વ્યાસ તરીકે લઈ દોરેલું વર્તુળ ચતુષ્કોણના વિકર્ણોના છેદબિંદુમાંથી પસાર થાય છે.
6. ABCD સમાંતરબાજુ ચતુષ્કોણ છે. A, B અને Cમાંથી પસાર થતું વર્તુળ CD(અથવા લંબાવેલી CD)ને Eમાં છેદે છે. સાબિત કરો કે, AE = AD.

7. એક વર્તુળની જીવાઓ AC અને BD એકબીજીને દુભાગે છે. સાબિત કરો કે, ( i ) AC અને BD વ્યાસ છે. (ii) ABCD લંબચોરસ છે.


Δ ABCના ખૂણાઓ A, B અને Cના દ્વિભાજકો તેના પરિવૃત્તને અનુક્રમે D, E અને Fમાં છેદે છે.

9. બે સમાન વર્તુળો એકબીજાને A અને B બિંદુએ છેદે છે. Aમાંથી એક રેખાખંડ PAQ એવી રીતે દોરેલો છે કે જેથી P અને Q વર્તુળો પર હોય. સાબિત કરો કે, BP = BQ.
X અને Y કેન્દ્રવાળાં બે સમાન વર્તુળો A અને Bમાં છેદે છે. આથી AB તેમની સામાન્ય જીવા છે.
સમાન વર્તુળોમાં સમાન જીવાઓ કેન્દ્ર આગળ સમાન ખૂણા આંતરે.
∴ ∠AXB = ∠AYB
X કેન્દ્રિત વર્તુળમાં ∠AXB = 2∠ APB અને
Y કેન્દ્રિત વર્તુળમાં ∠AYB = 2∠ AQB
∴ 2∠APB = 2∠ AQB
∴ ∠APB = ∠AQB
∴ ∠QPB = ∠PQB
Δ BPOમાં ∠QPB = ∠PQB હોવાથી QB = PB થાય.
આમ, BP = BQ.
10. કોઈ પણ ત્રિકોણ ABCમાં જો ∠Aનો દુભાજક અને BCનો લંબદ્વિભાજક છેદતાં હોય, તો સાબિત કરો કે તેઓ ત્રિકોણ ABCના પરિવર્તુળ પર છેદે છે.

Δ ABCના ∠Aનો દુભાજક Δ ABCના પરિવર્તુળને Dમાં છેદે છે.
∴ ∠BAD = ∠CAD
વળી, ∠BAD = ∠BCD અને ∠CAD = ∠CBD (એક જ વૃત્તખંડના ખૂણા)
∴ ∠BCD = ∠CBD
આમ, Δ BCDમાં ∠BCD = ∠CBD હોવાથી BD = CD મળે.
આમ, બિંદુ D એ B અને Cથી સમાન અંતરે આવેલ બિંદુ છે.
માટે, બિંદુ D એ BCના લંબદ્વિભાજકનું બિંદુ છે.
આમ, ∠Aનો દુભાજક અને BCનો લંબદ્વિભાજક D બિંદુમાં છેદે છે અને બિંદુ D Δ ABCના પરિવર્તુળનું બિંદુ છે.
આથી Δ ABCમાં જો ∠Aનો દુભાજક અને BCનો લંબદ્વિભાજક છેદતાં હોય, તો તેઓ Δ ABCના પરિવર્તુળ પર છેદે.
નોંધ : જો Δ ABCમાં AB = AC હોય, તો ∠Aનો દુભાજક અને BCનો લંબદ્વિભાજક એક જ રેખા પર હોય એટલે છે નહીં.
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here