Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 13 પૃષ્ઠફળ અને ઘનફળ
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 13 પૃષ્ઠફળ અને ઘનફળ
સ્વાધ્યાય – 13.1
1. એક 1.5 મી લાંબો, 1.25 મી પહોળો અને 65 સેમી ઊંડો પ્લાસ્ટિકનો ડબો બનાવવો છે. તેનું મથાળું ખુલ્લું છે. પ્લાસ્ટિક શીટની જાડાઈ અવગણતાં ( i ) ડબો બનાવવા જરૂરી શીટનું ક્ષેત્રફળ શોધો. (ii) 1 મી2 શીટના ₹ 20 લેખે થતો ખર્ચ શોધો.
પ્લાસ્ટિકનો ખુલ્લો ડબો બનાવવો છે માટે તેના પાર્શ્વપૃષ્ઠો તેમજ તળિયું બનાવવું છે.

2. એક રૂમની લંબાઈ, પહોળાઈ અને ઊંચાઈ અનુક્રમે 5 મી, 4 મી અને ૩ મી છે. રૂમની દીવાલ અને છતર7.50 પ્રતિ મી પ્રમાણે રંગવાનો ખર્ચ શોધો.
રૂમ માટે લંબાઈ l = 5 મી, પહોળાઈ b = 4 મી અને ઊંચાઈ h = 3 મી.
રંગવાલાયક વિસ્તારનું ક્ષેત્રફળ
= ચાર દીવાલોનું ક્ષેત્રફળ + છતનું ક્ષેત્રફળ
= 2h (l + b) + l × b
= 2 × 3 (5 + 4) + 5 × 4 મી2
= 54 + 20 મી2
= 74 મી2
1 મી2 વિસ્તારને રંગવાનો ખર્ચ = ₹ 7.5
∴ 74 મી2 વિસ્તારને રંગવાનો ખર્ચ = ₹ (74 × 7.5)
= ₹ 555
3. લંબચોરસ હૉલના તળિયાની પરિમિતિ 250 મી છે. જો ₹ 10 પ્રતિ મી2 લેખે તેની ચાર દીવાલ રંગવાનો ખર્ચ ₹ 15,000 થતો હોય, તો હૉલની ઊંચાઈ શોધો.
[સૂચના : ચાર દીવાલનું ક્ષેત્રફળ = પાર્શ્વપૃષ્ઠોનું પૃષ્ઠફળ]
₹ 10 ખર્ચમાં રંગાતા વિસ્તારનું ક્ષેત્રફળ = 1 મી2

4. એક ડબામાં 9.375 મી2 ક્ષેત્રફળ રંગી શકાય તેટલો રંગ છે. 22.5 સેમી × 10 સેમી × 7.5 સેમી માપની કેટલી ઈંટો આ ડબાના રંગથી રંગી શકાય?
ઈંટ માટે લંબાઈ l = 22.5 સેમી, પહોળાઈ b = 10 સેમી અને ઊંચાઈ h = 7.5 સેમી.
એક ઈંટનું કુલ પૃષ્ઠફળ

5. એક સમઘન પેટીની બધી જ ધાર 10 સેમી અને બીજી લંબઘન પેટીની લંબાઈ 12.5 સેમી, પહોળાઈ 10 સેમી અને ઊંચાઈ 8 સેમી છે.
(i) કઈ પેટીનાં પાર્શ્વપૃષ્ઠોનું ક્ષેત્રફળ વધુ છે? કેટલું?
(ii) કઈ પેટીનું કુલ પૃષ્ઠફળ ઓછું છે? કેટલું ?
(i) સમઘન પેટીની ધાર a = 10 સેમી
∴ સમઘન પેટીનાં પાર્શ્વપૃષ્ઠોનું ક્ષેત્રફળ = 4a2
= 4 (10)2 સેમી2
= 400 સેમી2
લંબધન પેટી માટે લંબાઈ l = 12.5 સેમી,
પહોળાઈ b = 10 સેમી અને ઊંચાઈ h = 8 સેમી.
લંબઘન પેટીનાં પાર્શ્વપૃષ્ઠોનું ક્ષેત્રફળ
= 2h (l + b)
= 2 × 8 (12.5 + 100 સેમી2
= 16 × 22.5 સેમી2
= 360 સેમી2
આમ, સમઘન પેટીના પાર્શ્વપૃષ્ઠોનું ક્ષેત્રફળ 40 સેમી2 (400 – 360) જેટલું વધુ છે.
(ii) સમઘન પેટીનું કુલ પૃષ્ઠફળ = 6a2
= 6 (10)2 સેમી2
= 600 સેમી2
લંબઘન પેટીનું કુલ પૃષ્ઠફળ
= 2 (lb + bh + hl)
= 2 (12.5 × 10 + 10 × 8 + 8 × 12.5) સેમી2
= 2 (125 + 80 + 100) સેમી2
= 2 (305) સેમી2
= 610 સેમી2
આમ, સમઘન પેટીનું કુલ પૃષ્ઠફળ 10 સેમી2 (610–600) જેટલું ઓછું છે.
6. ઘરમાં એક કાચનું ગ્રીનહાઉસ (તળિયા સાથે) બનાવેલ છે. તેને ટેપથી જોડેલ છે. જો તે 30 સેમી લાંબું, 25 સેમી પહોળું અને 25 સેમી ઊંચું હોય, તો ( i ) વપરાયેલ કાચનું ક્ષેત્રફળ કેટલું થશે? (ii) આ 12 ધાર માટે કેટલી ટેપની જરૂર પડે?
(i) લંબઘન આકારના ગ્રીનહાઉસ માટે લંબાઈ l = 30 સેમી, પહોળાઈ b = 25 સેમી અને ઊંચાઈ h = 25 સેમી.
ગ્રીનહાઉસ બનાવવા માટે વપરાયેલ કાચનું ક્ષેત્રફળ
= લંબઘનનું કુલ પૃષ્ઠફળ
= 2 (lb + bh + hl)
= 2 (30 × 25 + 25 × 25 + 25 × 30) સેમી2
= 2 (750 + 625 + 750) સેમી2
= 2 (2125) સેમી2
= 4250 સેમી2
(ii) લંબઘન આકારના ગ્રીનહાઉસની 12 ધાર પૈકી ચાર ધાર લંબાઈની, ચાર ધાર પહોળાઈની અને ચાર ધાર ઊંચાઈની હોય.
∴ 12 ધાર માટે જરૂરી ટેપની લંબાઈ
= 4l + 4b + 4h
= 4 (l + b + h)
= 4 (30 + 25 + 25) સેમી
= 4 (80) સેમી
= 320 સેમી
7. મીઠાઈની દુકાન, ‘શાંતિ મીઠાઈ’ કાગળના ખોખામાં મીઠાઈ પૅક કરવા ખોખા બનાવવાનો ઑર્ડર આપે છે. જુદાં જુદાં માપનાં બે પ્રકારના ખોખાની જરૂરિયાત છે. મોટા ખોખાનું માપ 25 સેમી × 20 સેમી × 5 સેમી અને નાના ખોખાનું માપ 15 સેમી × 12 સેમી × 5 સેમી છે. બધાંને ઢાંકવા કુલ પૃષ્ઠફળના 5 % વધુ જગ્યા જોઈશે. જો પૂંઠાનો ભાવ 1000 સેમી2 ના ₹ 4 હોય, તો બંને પ્રકારનાં 250 ખોખાં બનાવવાનો ખર્ચ શોધો.
લંબઘન આકારના મોટા ખોખા માટે લંબાઈ l = 25 સેમી, પહોળાઈ b = 20 સેમી અને ઊંચાઈ h = 5 સેમી.
મોટા ખોખાનું કુલ પૃષ્ઠફળ
= 2 (lb + bh + hl)
= 2 (25 × 20 + 20 × 5 + 5 × 25) સેમી2
= 2 (500 + 100 + 125) સેમી2
= 1450 સેમી2
ખોખાને ઢાંકવા માટે જોઈતા વધારાના પૂંઠાનું ક્ષેત્રફળ
= 1450ના 5% સેમી2
= 72.5 સેમી2
આમ, એક મોટા ખોખા માટે જરૂરી પૂંઠાનું ક્ષેત્રફળ
= 1450 + 72.5 સેમી2 = 1522.5 સેમી2
∴ 250 મોટા ખોખા માટે જરૂરી પૂંઠાનું ક્ષેત્રફળ
= (1522.5 × 250) સેમી2
લંબઘન આકારના નાના ખોખા માટે લંબાઈ l = 15 સેમી, પહોળાઈ b = 12 સેમી અને ઊંચાઈ h = 5 સેમી.
નાના ખોખાનું કુલ પૃષ્ઠફળ
= 2 (lb + bh + hl)
= 2 (15 × 12 + 12 × 5 + 5 × 15) સેમી2
= 2 (180 + 60 + 75) સેમી2
= 2 (315) સેમી2
= 630 સેમી2
ખોખાને ઢાંકવા માટે જોઈતા વધારાના પૂંઠાનું ક્ષેત્રફળ
= 630ના 5 % સેમી2
= 31.5 સેમી2
આમ, એક નાના ખોખા માટે જરૂરી પૂંઠાનું ક્ષેત્રફળ
= 630 + 31.5 સેમી2 = 661.5 સેમી2
∴ 250 નાના ખોખા માટે જરૂરી પૂંઠાનું ક્ષેત્રફળ
= (661.5 × 250) સેમી2
આમ, કુલ જરૂરી પૂંઠાનું ક્ષેત્રફળ
= (1522.5 × 250) + (661.5 × 250) સેમી2
= 250 (1522.5 + 661.5) સેમી2
= 250 × 2184 સેમી2
1000 સેમી2 પૂંઠાનો ખર્ચ = ₹ 4

8. પરવીન તેની ગાડી ઢાંકવા જેની ચાર બાજુઓ અને મથાળું તાડપત્રીથી બનાવેલ હોય તેવા માળખાવાળી કામચલાઉ પેટી (તેનો આગળનો ભાગ વીંટાળી શકાય તેવા ઢાંકણ જેવો હોય) આકારનું માળખું રચવા ઇચ્છે છે. માની લઈએ કે સિલાઈકામમાં ખૂબ ઓછી જગ્યા વપરાય છે. તેને અવગણી શકાય તો 2.5 મી ઊંચી અને 4 મી × 3 મી આધારવાળી પેટી માટે કેટલી તાડપત્રી જોઈશે?
તળિયા વગરની લંબઘન પેટી માટે લંબાઈ l = 4 મી, પહોળાઈ b = 3 મી અને ઊંચાઈ h = 2.5 મી.
તળિયા વગરની લંબઘન પેટીનું કુલ પૃષ્ઠફળ
= ચાર પાર્શ્વપૃષ્ઠોનું ક્ષેત્રફળ + મથાળાનું ક્ષેત્રફળ
= 2h (l + b) + l × b
= 2 × 2.5 (4 + 3) + 4 × 3 મી2
= 35 + 12 મી2
= 47 મી2
સ્વાધ્યાય – 13.2
1. લંબવૃત્તીય નળાકારની ઊંચાઈ 14 સેમી અને વક્રસપાટીનું ક્ષેત્રફળ 88 સેમી2 છે, તો નળાકારના પાયાનો વ્યાસ શોધો.

2. ધાતુના પતરામાંથી 1 મીટર ઊંચાઈ અને 140 સેમી પાયાના વ્યાસવાળી બંધ નળાકાર ટાંકી બનાવવી છે. તે બનાવવા માટે કેટલા ચોરસ મીટર પતરાની જરૂર પડશે?

3. ધાતુની એક પાઇપ 77 સેમી લાંબી છે. તેના આડછંદ(Cross section)નો અંદરનો વ્યાસ 4 સેમી અને બહારનો વ્યાસ 4.4 સેમી છે, (જુઓ આકૃતિ) તો, ( i ) તેની અંદરની વક્રસપાટીનું ક્ષેત્રફળ, (ii) તેની બહારની વક્રસપાટીનું ક્ષેત્રફળ અને (iii) તેનું કુલ પૃષ્ઠફળ શોધો.



4. 120 સેમી લંબાઈવાળા રોલરનો વ્યાસ 84 સેમી છે. જો રમતના મેદાનને સમતલ બનાવવા માટે રોલરને 500 આંટા મારવા પડે, તો રમતના મેદાનનું ક્ષેત્રફળ કેટલા ચોરસ મીટર હશે?

5. એક નળાકાર આકારના થાંભલાની ઊંચાઈ 3.5 મીટર અને વ્યાસ 50 સેમી છે. થાંભલાની વક્રસપાટીને રંગવાનો ખર્ચ પ્રતિ મીના ₹ 12.50 હોય, તો રંગકામ માટે કુલ ખર્ચ શોધો.

1 મી2 રંગવાનો ખર્ચ = ₹ 12.50
∴ 5.5 મી2 રંગવાનો ખર્ચ = ₹ (12.50 × 5.5)
= ₹ 68.75
આમ, થાંભલાની વક્રસપાટીને રંગવાનો ખર્ચ ₹ 68.75 થાય.
6. એક નળાકારની વક્રસપાટીનું ક્ષેત્રફળ 4.4 મી2 છે. જો તેના પાયાની ત્રિજ્યા 0.7 મી હોય, તો તેની ઊંચાઈ શોધો.

7. એક કૂવાની અંદરની સપાટીનો વ્યાસ 3.5 મી છે. તે 10 મી ઊંડો છે, તો (i) અંદરની વક્રસપાટીનું ક્ષેત્રફળ શોધો. (ii) એક મીના ₹ 40 લેખે અંદરની વક્રસપાટીને પ્લાસ્ટર કરવાનો ખર્ચ કેટલો આવે?
નળાકાર કૂવાની અંદરની સપાટી માટે વ્યાસ d = 3.5 મી અને ઊંચાઈ (ઊંડાઈ) h = 10 મી.

8. પાણીને ગરમ કરવાના સાધનમાં એક 28 મી લાંબો અને 5 સેમી વ્યાસવાળો નળાકાર પાઇપ છે. સાધનની ગરમ થતી સપાટીનું કુલ ક્ષેત્રફળ શોધો.
નળાકાર પાઇપ માટે વ્યાસ d = 5 સેમી = 0.05 મી અને લંબાઈ એટલે કે ઊંચાઈ h = 28 મી. પાઇપની વક્રસપાટી ગરમ થાય. એટલે આપણે પાઇપની વક્રસપાટીનું ક્ષેત્રફળ શોધીએ.
નળાકાર પાઇપની વક્રસપાટીનું ક્ષેત્રફળ

9. (i) 4.5 મી ઊંચી અને 4.2 મી વ્યાસ ધરાવતી બંધ નળાકારીય પેટ્રોલની ટાંકીની વક્રસપાટીનું ક્ષેત્રફળ શોધો.
(ii) ટાંકી બનાવતી વખતે 1/12 ભાગનું સ્ટીલ નકામું ગયું હોય, તો ખરેખર કેટલું સ્ટીલ ઉપયોગમાં લેવાયું હશે ?

10. આકૃતિમાં લૅમ્પશેડની ફ્રેમ જુઓ. તેને સુશોભિત કપડાંથી ઢાંકેલ છે. ફ્રેમના પાયાનો વ્યાસ 20 સેમી અને ઊંચાઈ 30 સેમી છે. મથાળા અને તળિયા માટે 2.5 સેમીની જગ્યા તેને વાળવા માટે રાખેલી છે. લૅમ્પશેડને ઢાંકવા માટે કેટલું કાપડ જોઈશે તે શોધો.
નળાકાર લૅમ્પશેડને ઢાંકવા માટે વપરાતું કાપડ પણ નળાકાર સ્વરૂપમાં જ થશે,
કાપડના નળાકારનો વ્યાસ d = 20 સેમી અને
કાપડના નળાકારની ઊંચાઈ h
= લૅમ્પશેડની ઊંચાઈ + 2.5 સેમી + 2.5 સેમી (વાળવા માટેની જગ્યા)

11. વિદ્યાલયના વિદ્યાર્થીઓ કાર્ડબોર્ડમાંથી કે જેનો પાયો નળાકાર છે તેવું પેન-હૉલ્ડર બનાવવાની અને સજાવવાની હરીફાઈમાં ભાગ લે છે. દરેક પેન-હૉલ્ડરની ત્રિજ્યા 3 સેમી અને ઊંચાઈ 10.5 સેમી રાખવાની છે. વિદ્યાલયે હરીફાઈ માટે કાર્ડબોર્ડ આપવાના છે, જો 35 હરીફો હોય, તો આ હરીફાઈ માટે કેટલું કાર્ડબોર્ડ જોઈશે?
નળાકાર પેન-હૉલ્ડર ઉ૫૨થી ખુલ્લું હોય અને નીચે તળિયું હોય, આમ, નળાકાર પેન-હૉલ્ડર બનાવવા તેની વક્રસપાટીના ક્ષેત્રફળ અને તળિયાના ક્ષેત્રફળના સરવાળા જેટલું કાર્ડબોર્ડ જોઈએ.
અહીં, નળાકાર પેન-હૉલ્ડરની ત્રિજ્યા r = 3 સેમી અને ઊંચાઈ h = 10.5 સેમી.
1 પેન-હૉલ્ડર બનાવવા જરૂરી કાર્ડબોર્ડનું ક્ષેત્રફળ

સ્વાધ્યાય – 13.3
1. શંકુના પાયાનો વ્યાસ 10.5 સેમી અને તેની ત્રાંસી ઊંચાઈ 10 સેમી છે. તેની વક્રસપાટીનું ક્ષેત્રફળ શોધો.
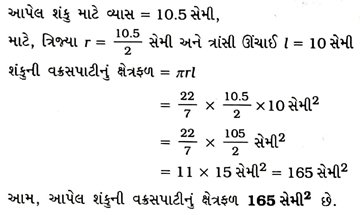
2. જેની ત્રાંસી ઊંચાઈ 21 મી અને પાયાનો વ્યાસ 24 મી હોય તેવા શંકુનું કુલ પૃષ્ઠફળ શોધો.

3. શંકુની વક્રસપાટીનું ક્ષેત્રફળ 308 સેમી? અને તેની ત્રાંસી ઊંચાઈ 14સેમી છે. આ શંકુની
(i) પાયાની ત્રિજ્યા અને (ii) કુલ સપાટીનું ક્ષેત્રફળ શોધો.
આપેલ શંકુ માટે, વક્રસપાટીનું ક્ષેત્રફળ = 308 સેમી2 અને ત્રાંસી ઊંચાઈ l = 14 સેમી.

4. શંકુ આકારનો તંબુ 10 મી ઊંચો છે અને તેના પાયાની ત્રિજ્યા 24 મી છે, તો ( i ) તંબુની ત્રાંસી ઊંચાઈ શોધો. (ii) 1 મી2 ના ₹ 70 લેખે તંબુ બનાવવા માટે વપરાતા કાપડનો કુલ ખર્ચ શોધો.

5. જેની ઊંચાઈ 8 મી અને પાયાની ત્રિજ્યા 6 મી હોય તેવા શંકુ આકારના તંબુ બનાવવા માટે 8મી પહોળી કેટલી તાડપત્રીની જરૂર પડે? માની લો કે સિલાઈના માપ અને કાપકૂપમાં થતાં બગાડમાં લગભગ 20 સેમી જેટલી વધારાની તાડપત્રી વપરાય છે. (π = 3.14 લો.)

આમ, તંબુ બનાવવા માટે 63 મી લંબાઈની તાડપત્રીની જરૂર પડે.
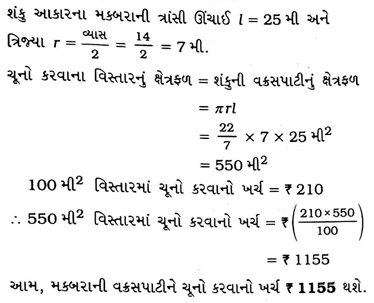
6. શંકુ આકારના મકબરાની ત્રાંસી ઊંચાઈ અને પાયાનો વ્યાસ અનુક્રમે 25 મી અને 14 મી છે. તેની વક્રસપાટી પર 100 મી2 ના ₹ 210 લેખે ચૂનો કરવાનો ખર્ચ શોધો.
7. એક જોકર(વિદૂષક)ની ટોપી લંબવૃત્તીય શંકુ આકારની છે. તેના પાયાની ત્રિજ્યા 7 સેમી અને ઊંચાઈ 24 સેમી છે. આવી 10 ટોપી બનાવવા વપરાતા કાગળનું ક્ષેત્રફળ શોધો.

1 ટોપી બનાવવા વપરાતા કાગળનું ક્ષેત્રફળ = 550 સેમી2
∴ 10 ટોપી બનાવવા વપરાતા કાગળનું ક્ષેત્રફળ
= 550 × 10 સેમી2
= 5500 સેમી2
આમ, 10 ટોપી બનાવવા વપરાતા કાગળનું ક્ષેત્રફળ 5500 સેમી2 થાય.
સ્વાધ્યાય – 13.4
1. આપેલ ત્રિજ્યા પરથી ગોળાની વક્રસપાટીનું ક્ષેત્રફળ શોધો :
(i) 10.5 સેમી
(ii) 5.6 સેમી
(iii) 14 સેમી

2. આપેલ વ્યાસ પરથી ગોળાની વક્રસપાટીનું ક્ષેત્રફળ શોધો :
(i) 14 સેમી
(ii) 21 સેમી
(iii) 3.5 મી

3. 10 સેમી ત્રિજ્યાવાળાં અર્ધગોળાનું કુલ પૃષ્ઠફળ શોધો.
(π = 3.14 લો.)
અહીં, અર્ધગોળાની ત્રિજ્યા r = 10 સેમી
અર્ધગોળાનું કુલ પૃષ્ઠફળ = 3πr2
= 3 × 3.14 × 10 × 10 સેમી2
= 942 સેમી2
4. એક ગોળાકાર ફુગ્ગામાં હવા ભરવાથી તેની ત્રિજ્યા 7 સેમીથી વધીને 14 સેમી થાય છે. આ બંને પરિસ્થિતિમાં ગોળાકાર ફુગ્ગાની વક્રસપાટીનાં ક્ષેત્રફળનો ગુણોત્તર શોધો.
મૂળ પરિસ્થિતિમાં ગોળાકાર ફુગ્ગાની ત્રિજ્યા r = 7 સેમી મૂળ પરિસ્થિતિમાં ફુગ્ગાની વક્રસપાટીનું ક્ષેત્રફળ

5. તાંબાના અર્ધગોળાકાર વાટકાની અંદરનો વ્યાસ 10.5 સેમી છે. તેની અંદર સપાટીને 100 સેમી2 ના ₹ 16 લેખે કલાઈ કરવાનો ખર્ચ કેટલો થાય?

આમ, વાટકાની અંદરની સપાટીને ક્લાઈ કરવાનો ખર્ચ ₹ 27.72 થાય.
6. જો ગોળાની વક્રસપાટીનું ક્ષેત્રફળ 154 સેમી? હોય, તો તેની ત્રિજ્યા શોધો.

7. જો ચંદ્રનો વ્યાસ પૃથ્વીના વ્યાસના આશરે ચોથા ભાગ જેટલો હોય, તો તેમની વક્રસપાટીઓનાં ક્ષેત્રફળનો ગુણોત્તર શોધો.

આમ, ચંદ્રની અને પૃથ્વીની વક્રસપાટીઓનાં ક્ષેત્રફળોનો ગુણોત્તર 1: 16 થાય.
8. સ્ટીલના અર્ધગોળાકાર વાટકાની જાડાઈ 0.25 સેમી છે. જો વાટકાની અંદરની સપાટીની ત્રિજ્યા 5 સેમી હોય, તો વાટકાની બહારની વક્રસપાટીનું ક્ષેત્રફળ શોધો.

9. એક લંબવૃત્તીય નળાકારમાં બંધ બેસે તે રીતે 7 ત્રિજ્યાવાળો એક ગોળો મૂકેલ છે, (જુઓ આકૃતિ) તો (1) ગોળાની વક્રસપાટીનું ક્ષેત્રફળ (ii) નળાકારની વક્રસપાટીનું ક્ષેત્રફળ (iii) ( i ) અને (ii)માં મળતાં ક્ષેત્રફળોનો ગુણોત્તર શોધો.

સ્વાધ્યાય – 13.5
1. દીવાસળીની એક પેટીનું માપ 4 સેમી × 2.5 સેમી x 1.5 સેમી છે, તો આવી 12 પેટી સમાય તેવી પેટીનું ઘનફળ કેટલું થાય?
દીવાસળીની લંબધન પેટી માટે લંબાઈ l = 4 સેમી, પહોળાઈ b = 2.5 સેમી અને ઊંચાઈ h = 1.5 સેમી.
દીવાસળીની લંબઘન પેટીનું ઘનફળ = l × b × h
= 4 × 2.5 × 1.5 સેમી3
= 15 સેમી3
∴ 12 દીવાસળીની પેટીનું ઘનફળ = 12 × 15 સેમી3
= 180 સેમી3
આમ, દીવાસળીની 12 પેટી સમાય તેવી પેટીનું ઘનફળ 180 સેમી3 થાય.
2. એક લંબઘન પાણીની ટાંકી 6મી લાંબી, 5 મી પહોળી અને 4.5મી ઊંડી છે. આ ટાંકીમાં કેટલા લિટર પાણી સમાઈ શકે? (1 મી3 = 1000 લિટર)
પાણીની લંબઘન ટાંકી માટે લંબાઈ l = 6 મી, પહોળાઈ b = 5 મી અને ઊંચાઈ h = 4.5 મી.
લંબઘન ટાંકીનું ઘનફળ = l × b × h
= 6 × 5 × 4.5 મી3
= 135 મી3
1 મી3 = 1000 લિટર
∴ 135 મી3 = 135000 લિટર
આમ, પાણીની ટાંકીમાં 1,35,000 લિટર પાણી સમાઈ શકે.
3. એક લંબઘન વાસણ 10 મી લાંબું અને 8 મી પહોળું છે. તેમાં 380 મી પ્રવાહી સમાઈ શકે, તો તેની ઊંચાઈ કેટલી?
લંબઘન વાસણ માટે લંબાઈ l = 10 મી, પહોળાઈ b = 8 મી અને ઊંચાઈ = h મી.
વાસણમાં 380 મી3 પ્રવાહી સમાઈ શકે છે. તેથી વાસણની ક્ષમતા અથવા ઘનફળ 380 મી3 છે.

4. 8 મી લંબાઈ, 6 મી પહોળાઈ અને ૭મી ઊંડાઈનો એક લંબઘન ખાડો ખોદવો છે. 1 મી3 ના ₹ 30 લેખે ખાડો ખોદવાનો ખર્ચ કેટલો થાય?
લંબઘન ખાડા માટે લંબાઈ l = 8 મી, પહોળાઈ b = 6 મી અને ઊંચાઈ (ઊંડાઈ) h = 3 મી.
લંબઘન ખાડો ખોદવા માટે કાઢવી પડતી માટીનું ઘનફળ
= લંબઘનનું ઘનફળ
= l × b × h
= 8 × 6 × 3 મી3
= 144 મી3
1 મી3 ખાડો ખોદવાનો ખર્ચ = ₹ 30
∴ 144 મી3 ખાડો ખોદવાનો ખર્ચ = ₹ (30 × 144)
= ₹ 4320
આમ, ખાડો ખોદવાનો ખર્ચ ₹ 4320 થાય.
5. એક લંબઘન પાણીની ટાંકીની ક્ષમતા 50,000 લિટર છે. જો તેની લંબાઈ અને ઊંડાઈ અનુક્રમે 2.5 મી અને 10 મી હોય, તો તેની પહોળાઈ શોધો.

6. એક ગામમાં 4000 લોકો રહે છે. દરેક વ્યક્તિની એક દિવસની જરૂરિયાત 150 લિટર પાણીની છે. આ ગામમાં 20 મી × 15 મી × 6 મી માપની ટાંકી છે. આ ટાંકીનું પાણી ગામના લોકોને કેટલા દિવસ ચાલે?

7. એક ગોદામનું માપ 40 મી × 25 મી × 15 મી છે. આ ગોદામમાં 1.5 મી × 1.25 મી × 0.5 મી માપનાં કેટલાં લાકડાંનાં ખોખાં સમાય?
ગોદામ માટે લંબાઈ l = 40 મી, પહોળાઈ b = 25 મી અને ઊંચાઈ h = 15 મી.
ગોદામનું ઘનફળ = l × b × h
= 40 × 25 × 15 મી3
લાકડાનાં ખોખાં માટે લંબાઈ l = 1.5 મી, પહોળાઈ b = 1.25 મી અને ઊંચાઈ h = 0.5 મી.
એક ખોખાનું ઘનફળ = l × b × h
= 1.5 × 1.25 × 0.5 મી3

8. 12 સેમી લંબાઈવાળા નક્કર ઘન પદાર્થને સરખા ઘનફળવાળા 8 ઘનમાં કાપવામાં આવે છે, તો નવા બનેલ ઘનની લંબાઈ કેટલી હશે? તેમના પૃષ્ઠફળનો ગુણોત્તર શોધો.


આમ, મૂળ ઘન અને નવા ઘનના પૃષ્ઠફળનો ગુણોત્તર 4:1 થાય.
9. ૩મી ઊંડાઈવાળી અને 40 મી પહોળાઈવાળી એક નદી 2 કિમી / કલાકની ઝડપથી વહે છે, તો તે 1 મિનિટમાં કેટલું પાણી સમુદ્રમાં ઠાલવશે ?

સ્વાધ્યાય – 13.6
1. નળાકાર વાસણના પાયાનો પરિઘ 132 સેમી અને ઊંચાઈ 25 સેમી છે. તેમાં કેટલા લિટર પાણી સમાય? (1000 સેમી3 = 1 લિટર)

2. એક નળાકાર લાકડાના પાઇપનો અંદરનો વ્યાસ 24 સેમી અને તેનો બહારનો વ્યાસ 28 સેમી છે. પાઇપની લંબાઈ 35 સેમી છે. જો 1 સેમી3 લાકડાનું દળ 0.6 ગ્રામ હોય, તો પાઇપનું દળ શોધો.


3. એક ઠંડું પીણું બે પ્રકારનાં પાત્રોમાં મળે છે :
(i) જેની લંબાઈ 5 સેમી, પહોળાઈ 4 સેમી અને ઊંચાઈ 15 સેમી છે એવું એક લંબચોરસ પાયાવાળું પતરાનું પાત્ર.
(ii) જેના વર્તુળાકાર પાયાનો વ્યાસ 7 સેમી અને ઊંચાઈ 10 સેમી છે એવું પ્લાસ્ટિકનું નળાકાર પાત્ર.
કયા પાત્રની ક્ષમતા વધુ છે? કેટલી?

4. એક નળાકારની વક્રસપાટીનું ક્ષેત્રફળ 94.2 સેમી અને તેની ઊંચાઈ 5 સેમી હોય, તો ( i ) તેની પાયાની ત્રિજ્યા અને (ii) તેનું ઘનફળ શોધો. (π = 3.14 લો.)

5. 10 મીટર ઊંડા એક નળાકાર વાસણની અંદરની સપાટીને રંગવાનો ખર્ચ ₹ 2200 થાય છે. જો રંગવાનો ખર્ચ 1 મી2 ના ₹ 20 હોય, તો ( i ) વાસણની અંદરની વક્રસપાટીનું ક્ષેત્રફળ, (ii) પાયાની ત્રિજ્યા અને (iii) વાસણની ક્ષમતા શોધો.

6. 1 મી ઊંચાઈવાળા બંધ નળાકાર વાસણની ક્ષમતા 15.4 લિટર છે, તો તે બનાવવા કેટલા ચોરસ મીટર ધાતુના પતરાની જરૂર પડશે?


7. એક પેન્સિલ લાકડાના પાયા નળાકાર અને તેની અંદરના ભાગમાં ચુસ્ત રીતે બેસે તેવા નક્કર ગ્રેફાઇટના નળાકારની બનેલી છે. પેન્સિલનો વ્યાસ 7 મિમી અને ગ્રેફાઇટનો વ્યાસ 1 મિમી છે. જો પેન્સિલની લંબાઈ 14 સેમી હોય, તો લાકડાનું અને ગ્રેફાઇટનું ઘનફળ શોધો.

8. એક હૉસ્પિટલમાં દર્દીઓને 7 સેમી વ્યાસવાળા નળાકાર પાત્રમાં સૂપ આપવામાં આવે છે. જો સૂપ 4 સેમી ઊંચાઈ સુધી ભરવામાં આવતું હોય, તો હૉસ્પિટલમાં રોજ 250 દર્દીઓને આપવા માટે કેટલું સૂપ બનાવવું પડે?



સ્વાધ્યાય – 13.7
1. નીચેનાં લંબવૃત્તીય શંકુનું ઘનફળ શોધો :
(i) ત્રિજ્યા 6 સેમી, ઊંચાઈ 7 સેમી
(ii) ત્રિજ્યા 3.5 સેમી, ઊંચાઈ 12 સેમી

2. નીચેના શંકુ આકારના વાસણની ક્ષમતા લિટરમાં શોધો :
(i) ત્રિજ્યા 7 સેમી, ત્રાંસી ઊંચાઈ 25 સેમી
(ii) ઊંચાઈ 12 સેમી, ત્રાંસી ઊંચાઈ 13 સેમી


3. એક શંકુની ઊંચાઈ 15 સેમી છે. જો તેનું ઘનફળ 1570 સેમી હોય, તો તેના પાયાની ત્રિજ્યા શોધો. (π = 3.14 લો.)
શંકુનું ઘનફળ = 1570 સેમી3, ઊંચાઈ h = 15 સેમી અને ત્રિજ્યા = r.
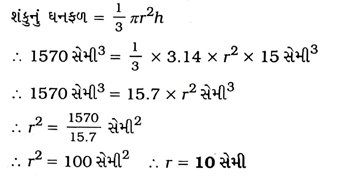
4. એક લંબવૃત્તીય શંકુનું ઘનફળ 48π સેમીૐ છે. તેની ઊંચાઈ 9 સેમી હોય, તો તેના પાયાનો વ્યાસ શોધો.
શંકુનું ઘનફળ = 48π સેમી3, ઊંચાઈ h = 9 સેમી અને ત્રિજ્યા = r.
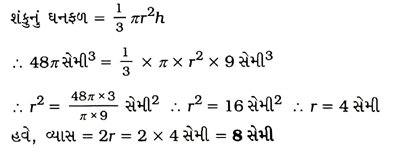
5. એક શંકુ આકારના ખાડાના ઉપરના ભાગનો વ્યાસ 3.5 મી અને ઊંડાઈ 12 મી છે. તેની ક્ષમતા (કિલોલિટરમાં) કેટલી થાય?

6. લંબવૃત્તીય શંકુનું ઘનફળ 9856 સેમી છે. તેના પાયાનો વ્યાસ 28 સેમી છે, તો ( i ) શંકુની ઊંચાઈ, (ii) શંકુની ત્રાંસી ઊંચાઈ અને (iii) શંકુની વક્રસપાટીનું ક્ષેત્રફળ શોધો.

7. કાટકોણ ત્રિકોણ ABCની બાજુનાં માપ 5 સેમી, 12 સેમી અને 13 સેમી છે. જો તેને 12 સેમીની બાજુ તરફ પરિભ્રમણ કરવામાં આવે, તો તેથી બનતા શંકુનું ઘનફળ શોધો.

8. ઉપરનાં દાખલા 7માં આપેલ ત્રિકોણ ABCનું 5 સેમી લંબાઈવાળી બાજુની આસપાસ પરિભ્રમણ કરવામાં આવે છે, તો આ રીતે બનતા ઘનનું ઘનફળ શોધો તથા દાખલા 7 અને 8માં બનતા શંકુના ઘનફળનો ગુણોત્તર શોધો.
5 સેમી, 12 સેમી અને 13 સેમી બાજુઓવાળા ત્રિકોણને 5 સેમીની બાજુની આસપાસ પરિભ્રમણ કરવાથી મળતા શંકુ


9. એક શંકુ આકારના ઘઉંના ઢગલાના પાયાનો વ્યાસ 10.5 મી અને ઊંચાઈ ૩ મી છે. તેનું ઘનફળ શોધો. આ ઢગલાને વરસાદથી બચાવવા કેંનવાસથી ઢાંકવામાં આવે છે, તો આ માટે જરૂરી કૅનવાસનું ક્ષેત્રફળ શોધો.

સ્વાધ્યાય – 13.8
1. આપેલ ત્રિજ્યા પરથી ગોળાનું ઘનફળ શોધો :
(i) 7 સેમી
(ii) 0.68 મી

2. આપેલ વ્યાસવાળા નક્કર ગોળા દ્વારા વિસ્થાપિત થતા પાણીનું કદ શોધો :
(i) 28 સેમી
(ii) 0.21 મી

3. એક ધાતુના ગોળાનો વ્યાસ 4.2 સેમી છે. જો તેના દ્રવ્યની ઘનતા 8.9 ગ્રામ / સેમી3 હોય, તો તેનું દળ શોધો.

4. જો ચંદ્રનો વ્યાસ આશરે પૃથ્વીના વ્યાસના ચોથા ભાગ જેટલો હોય, તો પૃથ્વીના ઘનફળ અને ચંદ્રના ઘનફળનો ગુણોત્તર શોધો.
ચંદ્રનો વ્યાસ પૃથ્વીના વ્યાસના ચોથા ભાગ જેટલો હોય, તો ચંદ્રની ત્રિજ્યા પૃથ્વીની ત્રિજ્યાના ચોથા ભાગ જેટલી જ હોય. બીજા શબ્દોમાં પૃથ્વીની ત્રિજ્યા ચંદ્રની ત્રિજ્યા કરતાં ચાર ગણી હોય. જો ચંદ્રની ત્રિજ્યા = r અને પૃથ્વીની ત્રિજ્યા = R લઈએ, તો R = 4r થાય.

5. 10.5 સેમી વ્યાસવાળા અર્ધગોળાકાર પાત્રમાં કેટલા લિટર દૂધ સમાવી શકાય?

6. એક અર્ધગોળાકાર ટાંકી 1 સેમી જાડા લોખંડના પતરામાંથી બનાવેલી છે. જો તેની અંદરની ત્રિજ્યા 1 મી હોય, તો આ ટાંકી બનાવવા વપરાયેલા લોખંડનું ઘનફળ શોધો.

7. એક ગોળાની વક્રસપાટીનું ક્ષેત્રફળ 154 સેમી હોય, તો તેનું ઘનફળ શોધો.

8. એક મકાનનો ઘુમ્મટ અર્ધગોળાકાર છે. તેની અંદરની બાજુએ ચૂનો લગાવવાનો ખર્ચ ₹ 4989.60 થાય છે. જો ચૂનો લગાવવાનો ખર્ચ 1 મી2 ના ₹ 20 હોય, તો ( i ) ઘુમ્મટની અંદરની વક્રસપાટીનું ક્ષેત્રફળ અને (ii) ઘુમ્મટની અંદર રહેલી હવાનું ઘનફળ શોધો.


9. જેની ત્રિજ્યા r અને વક્રસપાટીનું ક્ષેત્રફળ S હોય, તેવા 27 લોખંડના ગોળાને ઓગાળી તેમાંથી જેની વક્રસપાટીનું ક્ષેત્રફળ S હોય તેવો એક લોખંડનો ગોળો બનાવવામાં આવે છે, તો ( i ) નવા ગોળાની ત્રિજ્યા r’ અને (ii) S અને S’ ગુણોત્તર શોધો.
( i ) r ત્રિજ્યાવાળા 27 ગોળાને ઓગાળીને તેમાંથી r’ ત્રિજ્યાવાળો એક નવો ગોળો બનાવેલ છે.

10. એક ગોળાકાર દવાની કૅપ્સ્યૂલનો વ્યાસ 3.5 મિમી છે, તો આ કૅપ્સ્યૂલને સંપૂર્ણ રીતે ભરવા કેટલી દવાની (મિમી3) જરૂર પડશે?

હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરોઃ (ફક્ત અંતિમ જવાબ)
( 1 ) a ધારવાળા સમઘનનું પૃષ્ઠફળ = ………
( 2 ) નળાકારની વક્રસપાટીનું ક્ષેત્રફળ = …….
( 3 ) 1 હેક્ટર = …….. મી2
( 4 ) અર્ધગોળાનું ઘનફળ = ………
( 5 ) શંકુની કુલ સપાટીનું ક્ષેત્રફળ = ………
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) 7 સેમી વ્યાસના ગોળાનું ઘનફળ શોધો.
( 2 ) એક શંકુની ત્રિજ્યા 5 સેમી અને તિર્યક ઊંચાઈ 16 સેમી છે, તો તેની કુલ સપાટીનું ક્ષેત્રફળ શોધો.
( 3 ) 9 સેમી ત્રિજ્યાવાળા ધાતુના ગોળાને પિગાળીને 3 સેમી ત્રિજ્યાવાળા કેટલા ગોળા બને તે શોધો.
( 4 ) 15 સેમી ત્રિજ્યાવાળા એક શંકુની વક્રસપાટીનું ક્ષેત્રફળ 1650 સેમી હોય, તો તેની તિર્યક ઊંચાઈ શોધો.
( 5 ) એક ગોળાની સપાટીનું ક્ષેત્રફળ 5544 સેમી છે, તો તેનો વ્યાસ શોધો.
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) 12 સેમી ધાર ધરાવતા સમઘનનું ઘનફળ ……. સેમી3 થાય.
A. 864
B. 1728
C. 1296
D. 576
( 2 ) એક શંકુનું ઘનફળ 6160 સેમી અને ઊંચાઈ 30 સેમી છે, તો તેની ત્રિજ્યા ……. સેમી હોય.
A. 7
B. 14
C. 21
D. 28
( 3 ) બે ગોળાના વ્યાસનો ગુણોત્તર 3 : 5 છે, તો તેમના ઘનફળોનો ગુણોત્તર ……… થાય.
A. 9 : 25
B. 25 : 9
C. 27 : 125
D. 125 : 27
(4) 1 લિટર = ………. સેમી3
A. 10
B. 100
C. 1000
D. 10,000
( 5 ) એક નળાકાર પાત્રમાં 30.8 લિટર શરબત સમાઈ શકે છે. જો પાત્રની ત્રિજ્યા 14 સેમી હોય, તો તેની ઊંચાઈ …….. મીટર હોય.
A. 50
B. 25
C. 1/4
D. 1/2
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) એક શંકુની ત્રિજ્યા 7 સમી અને ઊંચાઈ 15 સેમી છે, તો તેનું ઘનફળ 1540 સેમી થાય.
( 2 ) જો નળાકારની વક્રસપાટીનું ક્ષેત્રફળ અને તેનું ઘનફળ આંકડાકીય રીતે સમાન હોય, તો શંકુની ત્રિજ્યા 2 એકમ હોય.
( 3 ) 5 સેમી ત્રિજ્યા અને 12 સેમી ઊંચાઈવાળા શંકુની વક્રસપાટીનું ક્ષેત્રફળ 60 π સેમી2 થાય.
( 4 ) ગોળાની ત્રિજ્યામાં 10% વધારો કરવાથી તેના ઘનફળમાં 21 %નો વધારો થાય.
( 5 ) બે નળાકારની ત્રિજ્યાઓનો ગુણોત્તર 3 4 અને ઊંચાઈઓનો ગુણોત્તર 8: 9 હોય, તો તેમના ઘનફળોનો ગુણોત્તર 1 : 2 થાય.
જવાબો
1. ( 1 ) 6a2 ( 2 ) π rh ( 3 ) 10,000 ( 4 ) 2/3 πr3 ( 5 ) π r (l + r)
2. ( 1 ) 179½ સેમી3 ( 2 ) 330 સેમી2 (3) 27 ગોળા ( 4 ) 35 સેમી ( 5 ) 42 સેમી
3. ( 1 ) 1728 ( 2 ) 14 (3) 27:125 ( 4 ) 1000 ( 5 ) 1/2
4. ( 1 ) ખોટું ( 2 ) ખરું ( 3 ) ખોટું ( 4 ) ખોટું ( 5 ) ખરું
સ્વાધ્યાય 13.9 (પ્રકીર્ણ સ્વાધ્યાય)*
1. એક પુસ્તક મૂકવાના લાકડાના કબાટના બહિર્પરિમાણો આ મુજબ છે : ઊંચાઈ 110 સેમી, ઊંડાઈ 25 સેમી અને પહોળાઈ 85 સેમી. (જુઓ આકૃતિ) આ કબાટ બનાવવા 5 સેમી જાડા પાટિયાનો ઉપયોગ કરવામાં આવે છે. તેની બહારની સપાટી પૉલિશ કરવાની છે અને અંદરની સપાટીને રંગવાની છે. જો પૉલિશ કરવાનો ખર્ચ પ્રતિ સેમી2 20 પૈસા અને રંગવાનો ખર્ચ પ્રતિ સેમી2 10 પૈસા હોય, તો રંગકામ અને પૉલિશ કરવાનો ખર્ચ શોધો.
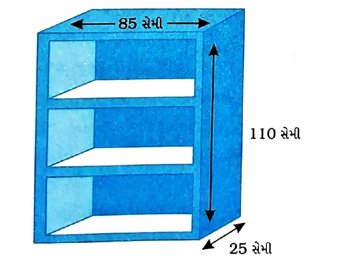
બહારના ભાગની પૉલિશ કરવાની કુલ સપાટીઓ :
( 1 ) કબાટનો પાછળનો ભાગ જેનું માપ (110 × 85) સેમી છે.
( 2 ) આજુબાજુના બે પડખા જે દરેકનું માપ (110 × 25) સેમી છે.
( 3 ) મથાળું અને તળિયું જે દરેકનું માપ (85 × 25) સેમી છે.
( 4 ) આગળના ભાગની બે ઊભી પટ્ટી જે દરેકનું માપ (110 × 5) સેમી છે.
( 5 ) આગળના ભાગની ચાર આડી પટ્ટી જે દરેકનું માપ (75 × 5) સેમી છે.
આમ, પૉલિશ કરવાની કુલ સપાટીનું ક્ષેત્રફળ
= [(110 × 85) + 2 (110 × 25) + 2 (85 × 25) + 2 (110 × 5) + 4 (75 × 5)] સેમી2
= (9350 + 5500 + 4250 + 1100 + 1500) સેમી2
= 21700 સેમી2
20 પૈસા પ્રતિ સેમી2 = ₹ 0.20 પ્રતિ સેમી2
1 સેમી2 વિસ્તારમાં પૉલિશ કરવાનો ખર્ચ = ₹ 0.20
∴ 21700 સેમી2 વિસ્તારમાં પૉલિશ કરવાનો ખર્ચ
= ₹ (21700 × 0.20) = ₹ 4340
અંદરના ભાગમાં રંગ કરવાની કુલ સપાટીઓ :
( 1 ) આજુબાજુનાં બે પડખાં જે દરેકનું માપ (90 × 20) સેમી છે.
( 2 ) બે પાટિયા દરેકની બે સપાટી અને બાટની મથાળા તથા તળિયાની બે સપાટી, એમ કુલ છ સપાટી જે દરેકનું માપ (75 × 20) સેમી છે.
( 3 ) કબાટનો પાછળનો ભાગ જેનું માપ (90 × 75) સેમી છે. આમ, રંગ કરવાની કુલ સપાટીનું ક્ષેત્રફળ
= [2 (90 × 20) + 6 (75 × 20) + (90 × 75)] સેમી2
= (3600 + 9000 + 6750) સેમી = 19350 સેમી2
10 પૈસા પ્રતિ સેમી2 = ₹ 0.10 પ્રતિ સેમી2
1 સેમી2 વિસ્તારમાં રંગ કરવાનો ખર્ચ = ₹ 0.10
∴ 19350 સેમી2 વિસ્તારમાં રંગ કરવાનો ખર્ચ
= ₹ (19350 × 0.10) = ₹ 1935
આથી પૉલિશ કરવાનો તથા રંગ કરવાનો કુલ ખર્ચ
= ₹ 4340 + 1935 = 76275
2. એક જમીનની બહાર આવેલ કોટ પર 21 સેમી વ્યાસવાળા લાકડાના ગોળાને નાના આધાર પર મૂકીને આકૃતિમાં દર્શાવ્યા મુજબ શણગારવામાં આવે છે. એ હેતુ માટે આવા 8 ગોળાનો ઉપયોગ કરવામાં આવે છે. ગોળાની નીચેનો નળાકાર આધાર 1.5 સેમી ત્રિજ્યા અને 7 સેમી ઊંચાઈવાળો છે. આ આધાર પર કાળો રંગ કરવાનો છે અને ગોળાને સિલ્વર રંગ કરવાનો છે. જો સિલ્વર રંગ કરવાનો ખર્ચ પ્રતિ સેમી2 25 પૈસા અને કાળો રંગ કરવાનો ખર્ચ 5 પૈસા પ્રતિ સેમી હોય, તો રંગ કરવાનો કુલ ખર્ચ શોધો.


3. એક ગોળાના વ્યાસમાં 25 % ઘટાડો કરતાં તેની વક્રસપાટીમાં કેટલા ટકા ઘટાડો થશે?

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here