Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 14 આંકડાશાસ્ત્ર
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 14 આંકડાશાસ્ત્ર
સ્વાધ્યાય – 14.1
1. તમે રોજિંદા જીવનમાંથી એકત્ર કરી શકો તેવી માહિતીનાં પાંચ ઉદાહરણ આપો.
રોજિંદા જીવનમાંથી એકત્ર કરી શકાય તેવી માહિતીનાં પાંચ ઉદાહરણ નીચે મુજબ આપી શકાય :
( 1 ) અખબાર અથવા ટેલિવિઝનમાંથી મેળવેલ ચૂંટણીનાં પરિણામ
( 2 ) આપણી શાળામાં ઉગાડેલ જુદાં જુદાં વૃક્ષોની સંખ્યા
( 3 ) છેલ્લા એક વર્ષનાં આપણાં ઇલેક્ટ્રિકનાં બિલ
( 4 ) શાળામાં જુદા જુદા ધોરણમાં ભણતાં વિદ્યાર્થીઓની સંખ્યા
( 5 ) આપણા વર્ગના વિદ્યાર્થીઓએ છેલ્લી પરીક્ષામાં મેળવેલ ગુણની ટકાવારી
2. ઉપરના પ્રશ્નની માહિતીનું પ્રાથમિક માહિતી અને ગૌણ માહિતીમાં વર્ગીકરણ કરો.
ઉપરના પ્રશ્ન 1ના જવાબમાં દર્શાવેલ પાંચ માહિતી પૈકી માહિતી નં. (2), (3) અને (5) પ્રાથમિક માહિતી છે, જે આપણે જાતે મેળવી શકીએ. પરંતુ માહિતી નં. (1) અને (4) ગૌણ માહિતી છે, કારણ કે તેમાં આપણે અખબાર અથવા ટેલિવિઝનમાં એકત્રિત કરવામાં આવેલ અને શાળાની ઑફિસમાં સંગ્રહવામાં આવેલ માહિતીનો ઉપયોગ કરીએ છીએ.
સ્વાધ્યાય – 14.2
1. ધોરણ 8ના 30 વિદ્યાર્થીઓના રુધિર-જૂથ(Blood group)ની વિગત નીચે મુજબ છે :
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O.
આ માહિતીને આવૃત્તિ-વિતરણ કોષ્ટકના સ્વરૂપમાં દર્શાવો. આ વિદ્યાર્થીઓના રુધિર-જૂથમાં ક્યું રુધિર-જૂથ સૌથી વધુ સામાન્ય છે અને કયું રુધિર-જૂથ સૌથી વધુ અસામાન્ય છે?

આવૃત્તિ-વિતરણ કોષ્ટક પરથી સ્પષ્ટ જણાય છે કે રુધિર-જૂથ O સૌથી વધુ સામાન્ય છે અને રુધિર-જૂથ AB સૌથી વધુ અસામાન્ય છે.
2. 40 ઇજનેરોનું ઘરથી નોકરીના સ્થાનનું અંતર (કિમીમાં) નીચે મુજબ છે :

ઉપર્યુક્ત માહિતીને 0 – 5નો (જેમાં 5 આવેલો નથી) પહેલો વર્ગ લઈ, 5ની વર્ગલંબાઈ લઈ એક વર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટક બનાવો. આ કોષ્ટકની રજૂઆત પરથી તમે કઈ મુખ્ય બાબતો તારવશો?

આ કોષ્ટકની રજૂઆત પરથી જણાય છે કે મોટા ભાગના એટલે કે 31 ઇજનેરોના ઘરથી નોકરીનું સ્થાન 5 કિમી અથવા 5 કિમીથી વધુ અને 20 કિમીથી ઓછું છે. થોડાક ઇજનેરો એટલે કે 5 ઇજનેરો માટે ઘરથી નોકરીનું સ્થાન 5 કિમીથી ઓછા અંતરે છે. વળી, થોડાક ઇજનેરો એટલે કે 4 ઇજનેરો માટે ઘરથી નોકરીનું સ્થાન 20 કિમી અથવા 20 કિમીથી વધુ અને 35 કિમીથી ઓછું છે.
3. 30 દિવસના એક મહિનામાં એક શહેરનો સાપેક્ષ ભેજ (% માં) નીચે પ્રમાણે આપેલ છે :
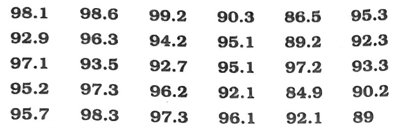
(i) બે વર્ગ 84 – 86, 86 – 88 વગેરે બને તે પ્રમાણે એક વર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટક બનાવો.
(ii) તમે કલ્પી શકો છો કે આ માહિતી કયા મહિનાની અથવા કઈ ઋતુની છે?
(iii) આ માહિતીનો વિસ્તાર શું છે?
(i)
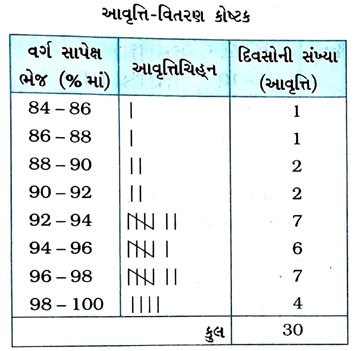
(ii) 30 દિવસમાંથી 24 દિવસ દરમિયાન સાપેક્ષ ભેજનું પ્રમાણ 92 % અથવા 92%થી વધુ છે. આ દર્શાવે છે કે આ માહિતી ચોમાસાની ઋતુમાં ભેગી કરવામાં આવેલ છે.
(iii) માહિતીનો વિસ્તાર = મહત્તમ અવલોકન – લઘુતમ અવલોકન
= 99.2 84.9
= 14.3
4. 50 વિદ્યાર્થીઓની પૂર્ણાંક સેન્ટિમીટરમાં માપવામાં આવેલી ઊંચાઈ નીચે પ્રમાણે જોવા મળી :

(i) ઉપર્યુક્ત માહિતીને 160 – 165, 165 – 170 વગેરે વર્ગો લઈને વર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટક રૂપે રજૂ કરો.
(ii) ઉપરના કોષ્ટક પરથી ઊંચાઈ વિશે તમે શું તારવી શકો?
(i)

(ii) ઉપરોક્ત કોષ્ટક પરથી તારવી શકાય છે કે 70 % વિદ્યાર્થીઓ(35 વિદ્યાર્થીઓ)ની ઊંચાઈ 165 સેમીથી ઓછી છે. ફક્ત 10 % વિદ્યાર્થીઓ(5 વિદ્યાર્થીઓ)ની ઊંચાઈ 170 સેમી અથવા તેથી વધુ છે.
5. કોઈ શહેરના વાતાવરણમાં સલ્ફર ડાયૉક્સાઇડની સાંદ્રતા ppm(parts per million)માં શોધવા માટેનો અભ્યાસ કરવામાં આવ્યો. તેની 30 દિવસમાં મળેલી માહિતી નીચે પ્રમાણે છે :

(i) માહિતીને 0.00 -0.04, 0.04 – 0.08, …. વગેરે વર્ગો લઈ વર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટક તૈયાર કરો.
(ii) કેટલા દિવસ સલ્ફર ડાયૉક્સાઇડની સાંદ્રતા 0.11 ppm કરતાં વધુ રહી હશે?
(i)
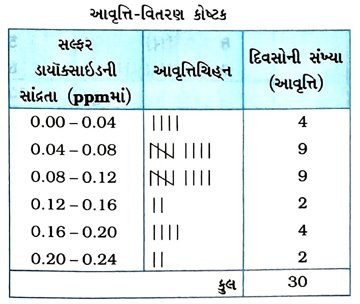
(ii) સલ્ફર ડાયૉક્સાઇડની સાંદ્રતા 8 દિવસ (2 + 4 + 2) 0.11 ppm કરતાં વધુ રહી છે.
6. ત્રણ સિક્કાઓને વારાફરતી 30 વખત ઉછાળવામાં આવતા દરેક વખત છાપ મળે તેની સંખ્યા નીચે પ્રમાણે નોંધાયેલી હતી :

7. π નું 50 દશાંશ-સ્થાન સુધી મૂલ્ય નીચે મુજબ છે :
3.
(i) દશાંશ-ચિહ્ન પછી 0થી 9 સુધી આવતાં અંકોનું આવૃત્તિ-વિતરણ બનાવો.
(ii) સૌથી વધુ વખત અને સૌથી ઓછી વખત કયો અંક આવે છે?
(i)
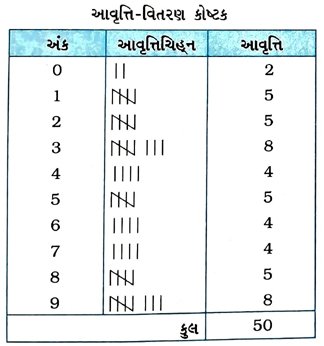
(ii) સૌથી વધુ વખત આવતા હોય તેવા અંકો 3 અને 9 છે. સૌથી ઓછી વખત આવતો હોય તેવો અંક 0 છે.
8. 30 બાળકોને પૂછવામાં આવ્યું કે ગયા અઠવાડિયામાં તેમણે કેટલા કલાક ટીવીના કાર્યક્રમ જોયા? તેનાથી મળતાં પરિણામો નીચે પ્રમાણે હતાં :

(i) આ માહિતીનું 5 વર્ગલંબાઈ લઈને અને એક વર્ગ 5 – 10 લઈને વર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટક તૈયાર કરો.
(ii) કેટલાં બાળકો અઠવાડિયામાં 15 કલાક કે તેથી વધુ કલાક ટેલિવિઝન જોતા હતા?
(i)
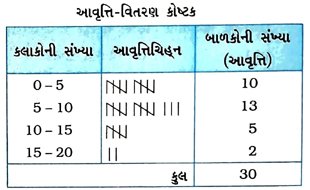
(ii) 2 બાળકો અઠવાડિયામાં 15 ક્લાક કે તેથી વધુ કલાક ટેલિવિઝન જોતા હતા.
9. એક કંપની એક વિશિષ્ટ પ્રકારની કાર-બૅટરી બનાવે છે. 40 બૅટરીના આયુષ્યની વર્ષમાં માહિતી નીચે મુજબ છે :

આ માહિતીનું 0.5 વર્ગલંબાઈ લઈ અને 2 − 2.5 વર્ગથી શરૂઆત કરીને એક વર્ગીકૃત આવૃત્તિ-વિતરણ કોષ્ટક બનાવો.

સ્વાધ્યાય – 14.3
1. કોઈ એક સંસ્થા દ્વારા 15થી 44 (વર્ષોમાં) વચ્ચેની વયવાળી સ્ત્રીની માંદગી અને મૃત્યુનાં કારણો શોધવા સર્વેક્ષણના નીચે પ્રમાણેના આંકડા (%માં) મળ્યા હતા :

(i) ઉપર આપેલી માહિતીની આલેખાત્મક રજૂઆત કરો.
(ii) વિશ્વમાં સ્ત્રીઓની માંદગી અને મૃત્યુ માટે કયું પરિબળ સૌથી વધુ કારણભૂત છે?
(iii) તમારા શિક્ષકની મદદથી ઉપર (11)માં દર્શાવ્યા સિવાયના અન્ય બે મુખ્ય પરિબળો શોધવાનો પ્રયત્ન કરો.
(i) 15 વર્ષથી 44 વર્ષ વચ્ચેની વયવાળી સ્ત્રીની માંદગી અને મૃત્યુનાં કારણો
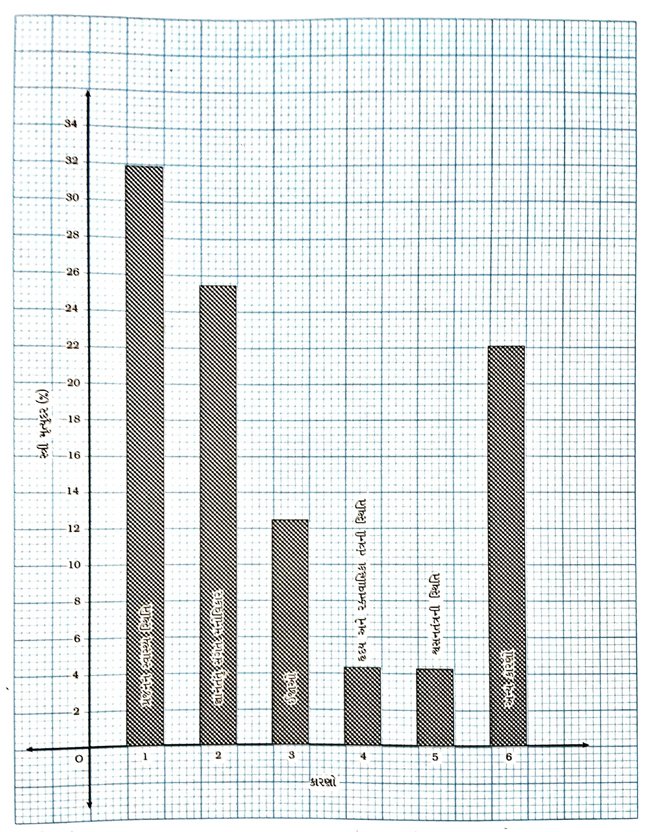
(ii) વિશ્વમાં સ્ત્રીઓની માંદગી અને મૃત્યુ માટેનું સૌથી વધુ કારણભૂત પરિબળ “પ્રજનન સ્વાસ્થ્ય સ્થિતિ” છે.
(iii) અન્ય મુખ્ય બે પરિબળોમાં “અપૂરતું પોષણ” અને “જરૂરી સ્વાસ્થ્ય સેવાઓનો અભાવ”ને ગણી શકાય.
2. ભારતીય સમાજના વિવિધ વિભાગોમાં હજાર છોકરાઓ દીઠ છોકરીઓની સંખ્યાઓની (લગભગ 10ના ગણિતની ન) માહિતી નીચે પ્રમાણે છે :

(i) ઉપર્યુક્ત માહિતીને આધારે લંબાલેખ દોરો.
(ii) આલેખ પરથી ક્યા તારણ કાઢી શકાય તેની વર્ગમાં ચર્ચા કરો.
(i) ભારતીય સમાજના વિવિધ વિભાગોમાં હજાર છોકરાઓ દીઠ છોકરીઓની સંખ્યા

3. એક રાજ્યની વિધાનસભાની ચૂંટણીમાં જુદા જુદા રાજકીય પક્ષોએ જીતેલી બેઠકો માટે મતદાનનું પરિણામ નીચે પ્રમાણે છે :

(i) મતદાનનાં પરિણામોને દર્શાવતો એક લંબાલેખ દોરો.
(ii) ક્યો રાજકીય પક્ષ સૌથી વધુ બેઠકો જીત્યો?
(i) જુદા જુદા રાજકીય પક્ષોએ જીતેલી બેઠકો

(ii) રાજકીય પક્ષ A સૌથી વધુ બેઠકો જીત્યો.
4. એક છોડનાં 40 પાંદડાંની લંબાઈ મિલિમીટરમાં આપવામાં આવી છે અને તેનાથી મળતી માહિતી નીચેના કોષ્ટકમાં દર્શાવી છે :

(i) આપેલી માહિતીનું નિરૂપણ કરતો એક સ્તંભાલેખ દોરો. [ સૂચન : સૌપ્રથમ વર્ગોને સતત બનાવો.]
(ii) શું અન્ય રીતે આ માહિતીની આલેખાત્મક રજૂઆત થઈ શકે?
(iii) 153 મિલિમીટર લંબાઈનાં પાંદડાંની સંખ્યા સૌથી વધુ છે. શું આ તારણ સાચું છે? કેમ?
વર્ગોને સતત બનાવતા નીચે પ્રમાણેનું આવૃત્તિ-વિતરણ કોષ્ટક મળે :
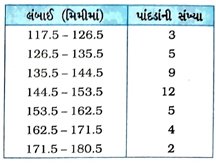
(i) લંબાઈ (મિમીમાં) પાંદડાંની સંખ્યા

(ii) હા, આ માહિતીની આલેખાત્મક રજૂઆત આવૃત્તિ બહુકોણ દ્વારા પણ થઈ શકે.
(iii) ના, દર્શાવેલ તારણ સાચું નથી. કારણ કે વર્ગ 145 – 153ની આવૃત્તિ 12 છે, પરંતુ તે દરેક અવલોક્નની ચોક્કસ કિંમત કઈ હોય તે અંગે કાંઈ જ કહી શકાય નહીં.
5. નીચેના કોષ્ટકમાં 400 નિયોન બલ્બનું આયુષ્ય આપેલું છે :

(i) આપેલી માહિતીને સ્તંભાલેખની મદદથી દર્શાવો. (ii) કેટલા બલ્બનું આયુષ્ય 700 કલાક અથવા 700 ક્લાકથી વધુ છે?
(i) 400 નિયોન બલ્બનું આયુષ્ય (કલાકમાં)
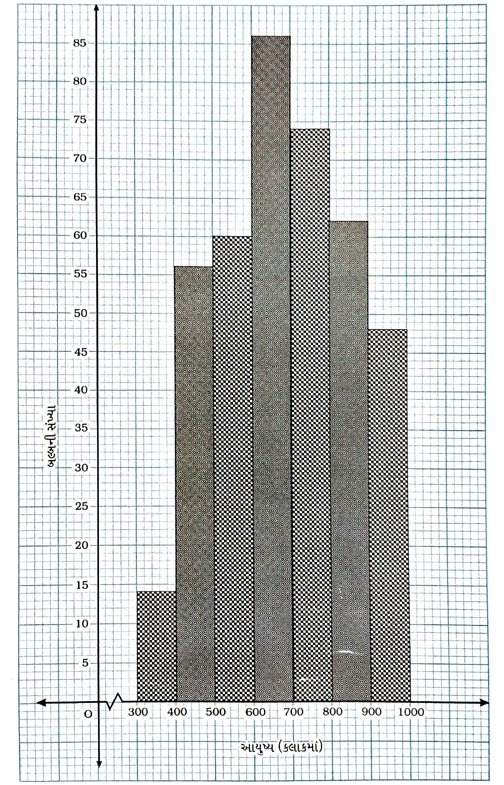
(ii) વર્ગ 700 – 800, 800 – 900 અને 900 – 1000ની આવૃત્તિ અનુક્રમે 74, 62 અને 48 છે. માટે 184 (74 + 62 + 48) બલ્બનું આયુષ્ય 700 કલાક અથવા 700 ક્લાકથી વધુ છે.
6. નીચેના કોષ્ટકમાં વિદ્યાર્થીઓએ મેળવેલા ગુણ અનુસાર તેમને બે વિભાગમાં વહેંચવામાં આવ્યા છે :
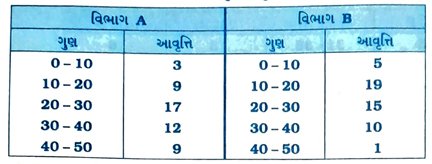
બંને વિભાગોના વિદ્યાર્થીઓએ મેળવેલા ગુણ એક જ આલેખમાં જુદા જુદા આવૃત્તિ બહુકોણ દ્વારા દર્શાવો. બંને આવૃત્તિ બહુકોણનો અભ્યાસ કરી બંને વિભાગના વિદ્યાર્થીના દેખાવની તુલના કરો.
બંને વિભાગના આવૃત્તિ બહુકોણ દોરવા માટે બંને વિભાગના વર્ગોની મધ્યકિંમતો શોધીને નીચે મુજબના કોષ્ટક બનાવીએ :


બંને વિભાગના વિદ્યાર્થીઓના દેખાવની તુલના કરતાં જણાય છે કે વિભાગ Aના વિદ્યાર્થીઓનો દેખાવ વિભાગ Bના વિદ્યાર્થીઓના દેખાવ કરતાં ચડિયાતો છે.
7. એક ક્રિકેટ-મૅચમાં બે ટીમો A અને B દ્વારા પ્રથમ 60 બૉલમાં કરેલા રનની માહિતી નીચે નોંધવામાં આવી છે :
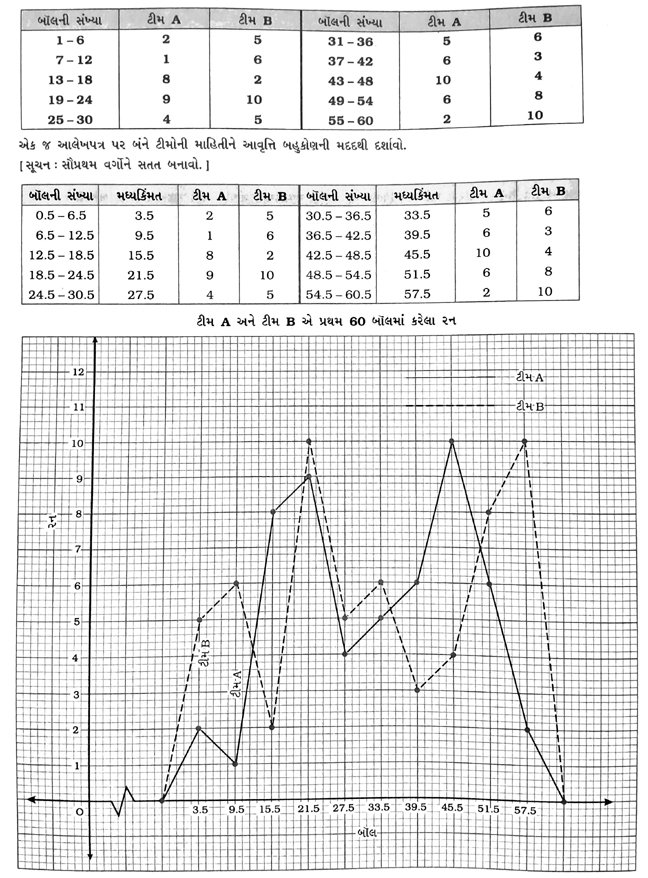
8. એક બગીચામાં રમતાં જુદાં જુદાં વય-જૂથનાં બાળકોની સંખ્યાનું યાદચ્છિક સર્વેક્ષણ કરવાથી નીચે પ્રમાણેની માહિતી પ્રાપ્ત થઈ :

9. એક સ્થાનિક ટેલિફોન ડિરેક્ટરીમાંથી યાદચ્છિક રીતે 100 અટક પસંદ કરવામાં આવી. તેમાંથી અંગ્રેજી મૂળાક્ષરોની સંખ્યાનું આવૃત્તિ-વિતરણ નીચે મુજબ પ્રાપ્ત થયું :
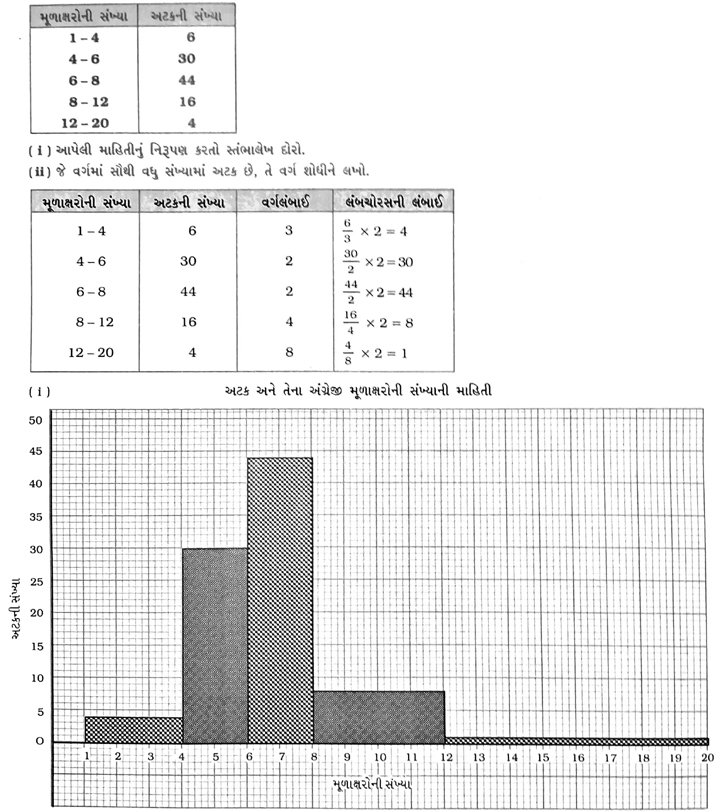
(ii) વર્ગ 6–8માં સૌથી વધુ સંખ્યામાં અટક છે.
સ્વાધ્યાય – 14.4
1. એક ટીમે એક શ્રેણીની 10 મૅચમાં કરેલા ગોલની સંખ્યા નીચે મુજબ છે :
2, 3, 4, 5, 0, 1, 3, 3, 4, 3
તો ગોલનો મધ્યક, મધ્યસ્થ અને બહુલક શોધો.

આમ, માહિતીનો મધ્યસ્થ 3 ગોલ છે.
માહિતીમાં અવલોકન 3 સૌથી વધુ વખત (4 વખત) પુનરાવર્તિત થાય છે. આથી માહિતીનો બહુલક 3 ગોલ છે.
2. ગણિતની કસોટીમાં 15 વિદ્યાર્થીઓએ 100માંથી મેળવેલા ગુણ નીચે પ્રમાણે નોંધાયેલા છે :
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
આ માહિતીનો મધ્યક, મધ્યસ્થ અને બહુલક શોધો


3. નીચેનાં અવલોકનો ચડતા ક્રમમાં ગોઠવેલા છે. જો માહિતીનો મધ્યસ્થ 63 હોય, તો x નું મૂલ્ય શોધો.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
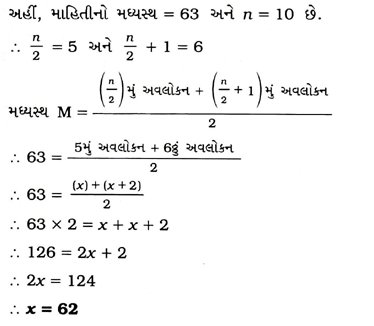
4. માહિતી 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18 નો બહુલક શોધો.
અહીં, માહિતીનું અવલોકન કરતાં પ્રથમ નજરે જ સ્પષ્ટ જણાય છે કે અવલોકન 14 ચાર વખત આવે છે. એટલે કે માહિતીમાં અવલોકન 14 સૌથી વધુ 4 વખત પુનરાવર્તિત થાય છે. આથી માહિતીનો બહુલક 14 છે.
5. નીચેના કોષ્ટકમાંથી એક ફૅક્ટરીમાં કામ કરતા 60 કર્મીઓના પગારનો મધ્યક શોધો :
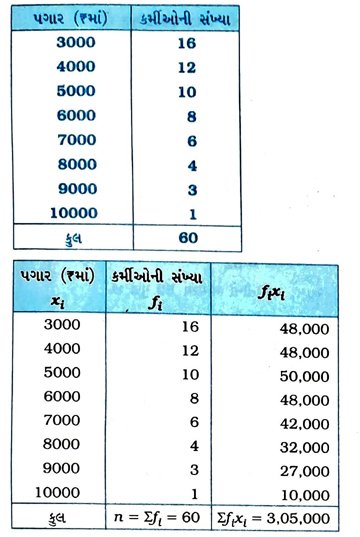

6. નીચે આપેલી માહિતી આધારિત એક ઉદાહરણ આપો :
(i) મધ્યક જ મધ્યવર્તી સ્થિતિમાનનું યોગ્ય માપ છે.
(ii) મધ્યક એ મધ્યવર્તી સ્થિતિમાનનું યોગ્ય માપ નથી, પરંતુ મધ્યસ્થ જ એક યોગ્ય માપ છે.
(i) શાળાના કોઈ વર્ગમાં ભણતા વિદ્યાર્થીઓનું જ્ઞાન સામાન્યતઃ એકસરખું જ હોય. અમુક જ વિદ્યાર્થી એવા હોય કે જેમના જ્ઞાનની કક્ષા વધુ પડતી ઊંચી અથવા વધુ પડતી નીચી હોય. આથી, શાળાના કોઈ વર્ગમાં ભણતા વિદ્યાર્થીઓના પરીક્ષામાં મેળવેલ ગુણ માટે મધ્યક જ મધ્યવર્તી સ્થિતિમાનનું યોગ્ય માપ છે.
(ii) કોઈ એક પ્રદેશના નાગરિકોની માસિક આવક અંગે વિચારીએ તો મધ્યક એ મધ્યવર્તી સ્થિતિમાનનું યોગ્ય માપ નથી, પરંતુ મધ્યસ્થ જ યોગ્ય માપ છે.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરોઃ (ફક્ત અંતિમ જવાબ)
( 1 ) ટેલિવિઝનમાંથી મેળવેલ ચૂંટણીનાં પરિણામ એ ……… માહિતી છે.
( 2 ) આપેલ વર્ગની ઊર્ધ્વસીમા અને અધઃસીમાના તફાવતને …….. કહે છે.
( 3 ) સ્તંભાલેખમાં x-અક્ષ પર ……… દર્શાવવામાં આવે છે.
( 4 ) અવલોકનો 14, 17, 40, 31, 38, 28નો મધ્યક ……. છે.
( 5 ) અવલોકનો 17, 21, 5, 12, 28, 10 અને ×નો મધ્યક 15 હોય, તો x = ……..
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) પ્રથમ બાર પ્રાકૃતિક સંખ્યાઓનો મધ્યસ્થ શોધો.
( 2 ) પ્રથમ પાંચ વિભાજ્ય સંખ્યાઓનો મધ્યક શોધો.
( 3 ) અવલોકનો 34, 55, 46, 72, 55, 62, 73, 85નો બહુલક શોધો.
( 4 ) અવલોકનો 82, 72, 87, 91, 75, 65, 85, 80-ì મધ્યસ્થ શોધો.
( 5 ) નીચેની માહિતીનો મધ્યક શોધો :
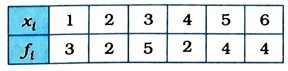
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) ચડતા ક્રમમાં આપેલ અવલોક્નો 15, 18, a + 1, a + 5, 32, 38નો મધ્યસ્થ 23 હોય, તો a = ………
A. 22
B. 21
C. 20
D. 24
( 2 ) અવલોકનો 82, 91, 98, 87, 92નો મધ્યક ……… થાય.
A. 450
B. 95
C. 85
D. 90
( 3 ) જો અવલોકનો 26, 18, x, 19, 24નો મધ્યક 20 હોય, તો x = ……..
A. 15
B. 17
C. 14
D. 13
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) અવલોકનો 2, 5, 1, 8, 15નો મધ્યસ્થ 6.5 છે.
( 2 ) પ્રથમ દસ પ્રાકૃતિક સંખ્યોઓનો મધ્યક 5 છે.
( 3 ) અવલોકનો 20, 20, – 20, 20, 20, − 20નો મધ્યક 0 છે.
( 4 ) માહિતીના મહત્તમ અવલોકન અને લઘુતમ અવલોકનના તફાવતને વિસ્તાર કહે છે.
( 5 ) સ્તંભાલેખ દોરવા પુ-અક્ષ પર વર્ગોના સીમાબિંદુઓ દર્શાવવામાં આવે છે.
જવાબો
1. ( 1 ) ગૌણ ( 2 ) વર્ગલંબાઈ ( 3 ) વર્ગસીમાબિંદુઓ ( 4 ) 28 ( 5 ) 12
2. ( 1 ) 6.5 ( 2 ) 7.4 ( 3 ) 55 ( 4 ) 81 ( 5 ) 3.7
3. ( 1 ) 20 ( 2 ) 90 ( 3 ) 13
4. ( 1 ) ખોટું ( 2 ) ખોટું ( 3 ) ખરું ( 4 ) ખરું ( 5 ) ખોટું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here