Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 15 સંભાવના
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 15 સંભાવના
સ્વાધ્યાય – 15.1
1. ક્રિકેટમાં, એક સી ખેલાડીએ 30 બૉલમાંથી 6 વાર દડાને ક્ષેત્રરેખા(boundary)ની બહાર મોકલ્યો. તેણે દડાને ક્ષેત્રરેખાની બહાર ન મોકલ્યો હોય તેની સંભાવના શોધો.
અહીં, 30 બૉલ રમવામાં આવ્યા. માટે કુલ પ્રયત્નોની સંખ્યા 30 થાય. બૉલને ક્ષેત્રરેખાની બહાર ન મોક્લ્યો હોય તે ઘટનાને A કહીએ, તો ઘટના A બની હોય તેવા બૉલની સંખ્યા 30 – 6 = 24 થાય.

2. બે બાળકો ધરાવતાં 1500 કુટુંબો યાદચ્છિક રીતે પસંદ કરવામાં આવ્યા અને નીચેની માહિતી પ્રાપ્ત થઈ :

યાદચ્છિક રીતે પસંદ કરેલ કુટુંબમાં
( i ) 2 છોકરીઓ હોય, (ii) 1 છોકરી હોય અને (iii) એક પણ છોકરી ન હોય. તેની સંભાવનાની ગણતરી કરો.
આ બધી સંભાવનાઓનો સરવાળો 1 થાય છે તે પણ ચકાસો.


3. ‘યાદ રાખો’ની વિશેષ સમજના દાખલા 5, પ્રકરણ 14નો વિચાર કરો. વર્ગનો વિદ્યાર્થી ઑગસ્ટ માસમાં જન્મ્યો હોય તેની સંભાવના શોધો.
જે દાખલાનો સંદર્ભ આપેલ છે તેના લંબાલેખ દ્વારા જે માહિતી મળે છે તે મુજબ વિદ્યાર્થીઓની કુલ સંખ્યા 40 છે અને તેમાં ઑગસ્ટ માસમાં જન્મ્યા હોય તેવા વિદ્યાર્થીઓની સંખ્યા 6 છે. આથી વિદ્યાર્થી ઑગસ્ટ માસમાં જન્મ્યો હોય તે ઘટનાને A કહીએ, તો ઘટના A બની હોય તેવા પ્રયત્નોની સંખ્યા 6 છે અને કુલ પ્રયત્નોની સંખ્યા 40 છે.

4. ત્રણ સિક્કાઓને એકસાથે 200 વખત ઉછાળતાં મળતાં પરિણામોની આવૃત્તિઓ નીચે પ્રમાણે છેઃ

5. કોઈ એક સંસ્થાએ યાદચ્છિક રીતે 2400 કુટુંબોને પસંદ કર્યાં અને તેમની આવક તેમજ તેમની પાસેનાં વાહનોની સંખ્યા જાણવા માટેનું સર્વેક્ષણ કર્યું. તેમાંથી પ્રાપ્ત માહિતી નીચેના કોષ્ટકમાં આપેલ છે :
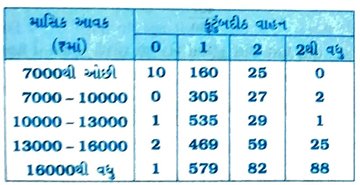
ધારો કે, યાદચ્છિક રીતે એક કુટુંબ પસંદ કરવામાં આવે છે. પસંદ કરેલ કુટુંબ માટે નીચે આપેલી માહિતી પરથી સંભાવના શોધો :
( i ) માસિક આવક ₹ 10000 – ₹ 13000 હોય અને તેમની પાસે ફક્ત 2. વાહન હોય.
(ii) માસિક આવક ₹ 16000થી વધુ હોય અને તેમની પાસે ફક્ત 1 જ વાહન હોય.
(iii) માસિક આવક ₹ 7000થી ઓછી હોય અને તેમની પાસે એક પણ વાહન ન હોય.
(iv) માસિક આવક ₹ 13000 – ₹ 16000 હોય અને તેમની પાસે 2થી વધુ વાહન હોય.
(v) એક કરતાં વધુ વાહન ન હોય.


6. કોષ્ટક 7, યાદ રાખો’ની વિશેષ સમજનો દાખલો 7 પ્રકરણ 14 ધ્યાનમાં લો.
(i) કોઈ વિદ્યાર્થીએ ગણિતની કસોટીમાં 20થી ઓછા ગુણ મેળવ્યા હોય તેની સંભાવના શોધો.
(ii) કોઈ વિદ્યાર્થીએ 60 કે તેથી વધુ ગુણ મેળવ્યા હોય તેની સંભાવના શોધો.
જે કોષ્ટકનો સંદર્ભ આપેલ છે તે મુજબ કુલ વિદ્યાર્થીઓની સંખ્યા 90 છે. માટે, એક વિદ્યાર્થી પસંદ કરવાના પ્રયોગમાં શક્યતાઓની કુલ સંખ્યા 90 થાય.
(i) તે જ કોષ્ટક મુજબ 20થી ઓછા ગુણ મેળવ્યા હોય તેવા વિદ્યાર્થીઓની સંખ્યા 7 છે. આથી વિદ્યાર્થીએ 20થી ઓછા ગુણ મેળવ્યા હોય તે ઘટનાને A કહીએ, તો ઘટના A બની હોય તેવા પ્રયત્નોની સંખ્યા 7 થાય.

(ii) તે જ કોષ્ટક મુજબ 60 કે તેથી વધુ ગુણ મેળવ્યા હોય તેવા વિદ્યાર્થીઓની સંખ્યા 15 + 8 23 છે. આથી વિદ્યાર્થીએ 60 કે તેથી વધુ ગુણ મેળવ્યા હોય તે ઘટનાને B કહીએ, તો ઘટના B બની હોય તેવા પ્રયત્નોની સંખ્યા 23 થાય.

7. આંકડાશાસ્ત્ર વિષય પ્રત્યેનો વિદ્યાર્થીઓનો અભિગમ જાણવા માટે 200 વિદ્યાર્થીઓનું સર્વેક્ષણ કરવામાં આવ્યું. તેની માહિતી નીચેના કોષ્ટકમાં દર્શાવેલી છે :

યાદચ્છિક રીતે કોઈ એક વિદ્યાર્થીને પસંદ કરતાં મળતી નીચેની ઘટનાની સંભાવના શોધો :
(i) આંકડાશાસ્ત્ર ગમે (ii) આંકડાશાસ્ત્ર ન ગમે
અહીં, કુલ વિદ્યાર્થીઓની સંખ્યા 200 છે. માટે, એક વિદ્યાર્થી પસંદ કરવાના પ્રયોગમાં પ્રયત્નોની કુલ સંખ્યા 200 થાય.
(i) વિદ્યાર્થીને આંકડાશાસ્ત્ર ગમે તે ઘટનાને A કહીએ, તો ઘટના A બને તેવા પ્રયત્નોની સંખ્યા 135 છે.

(ii) વિદ્યાર્થીને આંકડાશાસ્ત્ર ન ગમે તે ઘટનાને B કહીએ, તો ઘટના B બને તેવા પ્રયત્નોની સંખ્યા 65 છે.

8. સ્વાધ્યાય 14.2ના દાખલા 2નો વિચાર કરો. કોઈએ એક ઇજનેરને યાદચ્છિક રીતે પસંદ કરતાં મળતી નીચેની ઘટનાની સંભાવના શોધો :
(i) તેના કાર્યક્ષેત્રથી 7 કિમીથી ઓછા અંતરે રહેતા હોય.
(ii) તેના કાર્યક્ષેત્રથી 7 કિમી અથવા 7 કિમીથી વધુ અંતરે રહેતા હોય.
(iii) તેના કાર્યક્ષેત્રથી 1/2 કિમીથી ઓછા અંતરે રહેતા હોય.
સ્વાધ્યાય 14.2ના દાખલા 2માં આપેલ અવલોકનોની કુલ સંખ્યા 40 છે. માટે એક ઇજનેર પસંદ કરવાના પ્રયોગમાં પ્રયત્નોની કુલ સંખ્યા 40 છે.
(1) આપેલ અવલોકનોમાં 7 કિમીથી ઓછું અંતર હોય તેવા 9 અવલોકનો (5, 3, 2, 3, 6, 5, 6, 2, 3) છે. માટે, ઇજનેર તેના કાર્યક્ષેત્રથી 7 કિમીથી ઓછા અંતરે રહેતા હોય તે ઘટનાને A કહીએ, તો ઘટના A બની હોય તેવા પ્રયત્નોની સંખ્યા 9 છે.

(ii) હવે, બાકીનાં બધાં જ, એટલે કે 40 – 9 = 31 અવલોકનો 7 કિમી અથવા 7 કિમીથી વધુ અંતરના છે. માટે, ઇજનેર તેના કાર્યક્ષેત્રથી 7 કિમી અથવા 7 કિમીથી વધુ અંતરે રહેતા હોય તે ઘટનાને B કહીએ, તો ઘટના B બની હોય તેવા પ્રયત્નોની સંખ્યા 31 છે.

(iii) હવે, આપેલ અવલોકનોમાં 1/2 કિમીથી ઓછું અંતર હોય તેવું એક પણ અવલોકન નથી. માટે ઇજનેર તેના કાર્યક્ષેત્રથી 1/2 કિમીથી ઓછા અંતરે રહેતા હોય તે ઘટનાને C કહીએ, તો ઘટના C બની હોય તેવા પ્રયત્નોની સંખ્યા 0 છે.

9. પ્રવૃત્તિ : તમારી શાળાના દરવાજા આગળ ઊભા રહો અને ચોક્કસ સમયમર્યાદામાં દ્વિચક્રી વાહનો, ત્રિચક્રી વાહનો અને ચાર પૈડાવાળાં કેટલાં વાહનો પસાર થાય છે તેની આવૃત્તિ નોંધો. કુલ વાહનની સંખ્યામાંથી પસાર થતું વાહન દ્વિચક્રી વાહન હોય તેની સંભાવના શોધો.
નોંધ : આ પ્રવૃત્તિ વિદ્યાર્થીએ જાતે કરવી.
10. પ્રવૃત્તિ : તમારા વર્ગમાં રહેલા વિદ્યાર્થીઓને 3 અંકવાળી એક સંખ્યા લખવાનું કહો. યાદચ્છિક રીતે કોઈ એક વિદ્યાર્થી પસંદ કરો. પસંદ કરેલ વિદ્યાર્થી દ્વારા લખાયેલ સંખ્યા એ ૩થી વિભાજ્ય હોય તેની સંભાવના શોધો. યાદ રાખો કે જો આપેલી સંખ્યાના અંકોના સરવાળાને ૩ વડે નિઃશેષ ભાગી શકાય, તો આપેલ સંખ્યા એ 3 વડે વિભાજ્ય છે.
નોંધઃ આ પ્રવૃત્તિ વિદ્યાર્થીએ જાતે કરવી.
11. ઘઉંના લોટની થેલી પર 5 કિગ્રા વજન લખેલ હોય તેવી 11 થેલી પસંદ કરી. તેમાં ખરેખર કેટલો લોટ છે તે વજન (કિગ્રામાં) નીચે પ્રમાણે આપેલ છે :
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
આમાંની કોઈ એક થેલી યાદચ્છિક રીતે પસંદ કરતાં તેમાં લોટનું વજન 5 કિગ્રાથી વધુ હોય તેની સંભાવના શોધો.
અહીં, લોટની કુલ 11 થેલી આપેલ છે. માટે, એક થેલી પસંદ કરવાના પ્રયોગમાં પ્રયત્નોની કુલ સંખ્યા 11 થાય.
હવે, 5 કિગ્રાથી વધુ વજન ધરાવતી કુલ 7 થેલીઓ છે. (5.05, 5.08, 5.03, 5.06, 5.08, 5.04, 5.07). માટે, પસંદ કરેલ થેલીમાં લોટનું વજન 5 કિગ્રાથી વધુ હોય તે ઘટનાને A કહીએ, તો ઘટના A બની હોય તેવા 7 પ્રયત્નો છે.

12. સ્વાધ્યાય 14.2ના દાખલા 5નો વિચાર કરો. કોઈ એક શહેરમાં હવામાં સલ્ફર ડાયૉક્સાઇડની સાંદ્રતા શોધવા માટેનો પ્રયોગ કરવામાં આવ્યો. તે દસ લાખના ભાગમાં (ppm) 30 દિવસની માહિતીનું આવૃત્તિ-વિતરણ તૈયાર કરવાનું હતું. આ કોષ્ટકનો ઉપયોગ કરીને 0.12 – 0.16 વર્ગ માટે સલ્ફર ડાયૉક્સાઇડની સાંદ્રતાની સંભાવનાની ગણતરી કરો.
સ્વાધ્યાય 14.2ના દાખલા 5માં કુલ દિવસોની સંખ્યા 30 છે, માટે, કોઈ એક દિવસ પસંદ કરવામાં આવે તે પ્રયોગમાં દિવસોની કુલ સંખ્યા 30 છે.
તે જ કોષ્ટકમાં આપણે જોયું કે વર્ગ 0.12 – 0.16ની આવૃત્તિ 2 છે, એટલે કે 2 દિવસ દરમિયાન સલ્ફર ડાયૉક્સાઇડની સદ્રિતા (ppmમાં) 0.12 – 0.16 હતી. આથી જો સલ્ફર ડાયૉક્સાઇડની સાંદ્રતા (ppmમાં) 0.12 – 0.16 વર્ગમાં હોય તે ઘટનાને A કહીએ, તો ઘટના A બની હોય તેવા દિવસોની સંખ્યા 2 છે.

13. સ્વાધ્યાય 14.2ના દાખલા 1નો વિચાર કરો. એક વર્ગના 30 વિદ્યાર્થીઓના રુધિર-જૂથ માટેનું આવૃત્તિ-વિતરણ તૈયાર કરવાનું હતું, તો આ વિદ્યાર્થીઓમાંથી કોઈ એક વિદ્યાર્થીનું રુધિર-જૂથ AB હોય તેની સંભાવનાની ગણતરી કરો.
સ્વાધ્યાય 14.2ના દાખલા 1માં કુલ વિદ્યાર્થીઓની સંખ્યા 30 છે. માટે, એક વિદ્યાર્થીને પસંદ કરવાના પ્રયોગમાં પ્રયત્નોની કુલ સંખ્યા 30 છે.
હવે, AB રુધિર-જૂથ ધરાવતા વિદ્યાર્થીઓની સંખ્યા ૩ છે. માટે, જો કોઈ વિદ્યાર્થીનું રુધિર-જૂથ AB હોય તે ઘટનાને A કહીએ, તો ઘટના A બની હોય તેવા પ્રયત્નોની સંખ્યા 3 છે

હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરો : (ફક્ત અંતિમ જવાબ)
( 1 ) અશક્ય ઘટનાની સંભાવના ……… છે.
( 2 ) પ્રયોગ માટેની ઘટના એ પ્રયોગનાં કેટલાંક ……… નું એકત્રીકરણ છે.
( 3 ) એક પ્રયોગનાં ફક્ત બે જ શક્ય નિવારક પરિણામો A અને B છે. જો P (A) = 0.39 હોય, તો P (B) = …….
( 4 ) ચોક્કસ ઘટનાની સંભાવના …….. છે.
( 5 ) બધી જ પરસ્પર નિવારક ઘટનાઓની સંભાવનાનો સરવાળો ……… છે.
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) એક સિક્કાને 500 વખત ઉછાળતાં 230 વખત છાપ મળે છે, તો તે સિક્કાને ઉછાળતાં છાપ મળે તેની સંભાવના શોધો.
( 2 ) લૉટરીની 1000 ટિકિટમાંથી 50 ટિકિટમાં ઇનામ છે. આરીવ એક ટિકિટ ખરીદે તો તેને ઇનામ લાગવાની સંભાવના શોધો.
( 3 ) બે સિક્કા એકસાથે 1000 વખત ઉછાળતાં નીચે મુજબના પરિણામ મળ્યા : બે છાપ : 230 વખત; એક છાપ : 550 વખત; એક પણ છાપ નહીં : 220 વખત. બે છાપ મળવાની સંભાવના શોધો.
( 4 ) લીપ-વર્ષના ફેબ્રુઆરી માસમાં 5 ગુરુવાર આવે તેની સંભાવના શોધો.
( 5 ) જો ઘટના A બનવાની સંભાવના 13/20 હોય, તો ઘટના A ન બને તેની સંભાવના શોધો.
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) ઘટના A બનવાની સંભાવના x/2 છે અને ઘટના A ન બનવાની સંભાવના 2/3 છે, તો x = …….
A. 4/3
B. 3/4
C. 2/3
D. 1/3
( 2 ) એક સમતોલ પાસાને ફેંકવાથી મળતો અંક યુગ્મ હોય તેની સંભાવના ……… છે.
A. 1/2
B. 1/3
C. 1/4
D. 1/6
( 3 ) જો P (A) = 3 c. – D. • 6 0.56 અને ઘટના A ઉદ્ભવે તે માટેના પ્રયત્નોની સંખ્યા 28 હોય, તો કુલ પ્રયત્નોની સંખ્યા …… હોય.
A. 50
B. 100
C. 200
D. 400
( 4 ) બરાબર ચીપેલાં 52 પાંના ઢગમાંથી એક પત્તુ પસંદ કરતાં તે રાણી હોય તેની સંભાવના …….. છે.
A. 1/52
B. 1/16
C. 1/13
D. 1
( 5 ) 50 ગુણની પરીક્ષામાં 32 ગુણ મેળવવાની સંભાવના ……. છે.
A. 32/50
B. 32/51
C. 1/50
D. 1/51
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) સમતોલ પાસાને ઉછાળતાં તેની પર અંક 2 આવે તેની સંભાવના 1/3 છે.
( 2 ) બે સમતોલ સિક્કા એકસાથે ઉછાળતાં બંને પર કાંટો મળે તેની સંભાવના 1/2 છે.
( 3 ) કોઈ ઘટના Aની સંભાવના 5/3 હોઈ ન શકે.
( 4 ) લીપ-વર્ષમાં 53 રવિવાર આવે તેની સંભાવના 2/7 છે.
( 5 ) બરાબર ચીપેલાં 52 પત્તાંના ઢગમાંથી એક પત્તુ પસંદ કરતાં તે લાલ રંગનું હોય તેની સંભાવના 1/4 છે.
જવાબો
1. ( 1 ) 0 ( 2 ) પરિણામો ( 3 ) 0.61 ( 4 ) 1 ( 5 ) 1
2. ( 1 ) 0.46 ( 2 ) 0.05 ( 3 ) 0.23 (4) 1/7 ( 5 ) 7/20
3. ( 1 ) 2/3 ( 2 ) 1/2 ( 3 ) 50 ( 4 ) 1/13 ( 5 ) 1/51
4. ( 1 ) ખોટું ( 2 ) ખોટું ( 3 ) ખરું ( 4 ) રું ( 5 ) ખોટું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here