Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 3 યામ ભૂમિતિ
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 3 યામ ભૂમિતિ
સ્વાધ્યાય – 8.1
1. બીજી કોઈ વ્યક્તિને તમારા અભ્યાસના ટેબલ પરના ટેબલ લૅમ્પનું સ્થાન કેવી રીતે વર્ણવશો?
સૌપ્રથમ હું તે વ્યક્તિને સમજાવીશ કે મારું અભ્યાસ ટેબલ એ કાર્તેઝિય સમતલનું પ્રથમ ચરણ છે જેમાં મારી નજીક હોય તે ધાર એ x-અક્ષની ધન દિશા છે તથા મારા ડાબા હાથ તરફની ધાર એ પુ-અક્ષની ધન દિશા છે. હવે હું મારી નજીકની ધારથી ટેબલ લૅમ્પનું અંતર માપીશ. ધારો કે, તે ૫ સેમી છે. ત્યારબાદ, હું મારા ડાબા હાથ તરફની ધારથી ટેબલ લૅમ્પનું અંતર માપીશ. ધારો કે, તે x સેમી છે. હવે હું ટેબલ લૅમ્પનું સ્થાન વર્ણવવા માટે જણાવીશ કે તે મારી નજીકની ધારથી ૫ સેમી દૂર અને મારા ડાબા હાથ તરફની ધારથી x સેમી દૂર છે. આ રીતે બે સ્વતંત્ર માહિતીની મદદથી ટેબલ પર રહેલ ટેબલ લૅમ્પનું સ્થાન ચોકસાઈપૂર્વક વર્ણવી શકાય. y
2. (શેરીનો નકશો) એક શહેરના બે મુખ્ય રસ્તાઓ શહેરના કેન્દ્ર આગળ એકબીજાને છેદે છે. આ બે રસ્તાઓ ઉત્તર-દક્ષિણ દિશાઓ અને પૂર્વ-પશ્ચિમ દિશાઓમાં છે. શહેરની બાકીની બધી શેરીઓ આ રસ્તાની સમાંતરે છે અને પરસ્પર 200 મીટર દૂર છે. દરેક દિશામાં 5 શેરીઓ છે. 1 સેમી = 200 મીટર માપ લઈ તમારી નોટબુકમાં શહેરનું આદર્શ ચિત્ર દોરો. રસ્તાઓ / શેરીઓને સીધી રેખાઓ દ્વારા દર્શાવો.
તમારા નમૂનામાં શહેરમાં ઘણી બધી છેદતી શેરીઓ છે. આ છેદતી શેરીઓ એક ઉત્તર-દક્ષિણ દિશામાં અને બીજી પૂર્વપશ્ચિમ દિશામાં જતી હોય તેવી બે શેરીઓની બનેલી છે. દરેક લંબ શેરી નીચેના અનુસંધાનમાં દર્શાવાય છે. જો બીજી શેરી ઉત્તર-દક્ષિણ દિશામાં અને પાંચમી શેરી પૂર્વ-પશ્ચિમ દિશામાં ક્યાંક મળતી હોય, તો આપણે તેને છેદતી શેરી (2, 5) કહીશું. આ રૂઢિનો ઉપયોગ કરી નીચેના પ્રશ્નોના જવાબ આપો :
(i) કેટલી છેદતી શેરીઓનું નામાભિધાન (4, 3) તરીકે થઈ શકે?
(ii) કેટલી છેદતી શેરીઓનું નામાભિધાન (3, 4) તરીકે થઈ શકે?
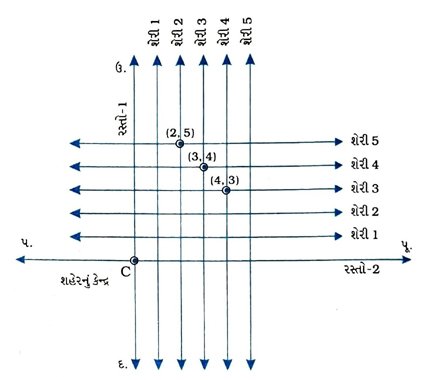
(i) છેદતી શેરીઓ પૈકી એક અને માત્ર એકનું જ (અનન્ય) નામાભિધાન (4, 3) તરીકે થઈ શકે, કારણ કે તે બિંદુ ઉત્તર-દક્ષિણ દિશામાં જતી ચોથી શેરી અને પૂર્વ-પશ્ચિમ દિશામાં જતી ત્રીજી શેરીનું છેદબિંદુ છે. આપણે બે સ્વતંત્ર માહિતીનો ઉપયોગ કરતા હોવાથી શેરીઓના દ૨ેક છેદબિંદુનું અનન્ય રીતે (x, y) નામાભિધાન કરી શકીએ.
(ii) છેદતી શેરીઓ પૈકી એક અને માત્ર એકનું જ (અનન્ય) નામાભિધાન (3, 4) તરીકે થઈ શકે, કારણ કે તે બિંદુ ઉત્તર-દક્ષિણ દિશામાં જતી ત્રીજી શેરી અને પૂર્વ-પશ્ચિમ દિશામાં જતી ચોથી શેરીનું છેદબિંદુ છે.
સ્વાધ્યાય – 8.2
1. નીચેના દરેક પ્રશ્નોના જવાબ આપો :
(i) યામ-સમતલમાં કોઈ પણ બિંદુ દર્શાવવા ઉપયોગમાં લેવાતી સમક્ષિતિજ અને શિરોલંબ રેખાઓનાં નામ શું છે?
(ii) આ બે રેખાઓથી બનતા સમતલના દરેક ભાગનું નામ શું છે?
(iii) આ બે રેખાઓ જ્યાં છેદે તે બિંદુનું નામ લખો.
(i) યામ-સમતલમાં કોઈ પણ બિંદુ દર્શાવવા ઉપયોગમાં લેવાતી સમક્ષિતિજ રેખાનું નામ ૮-અક્ષ અને શિરોલંબ રેખાનું નામ પુ-અક્ષ છે.
(ii) આ બે રેખાઓ (x-અક્ષ તથા પુ-અક્ષ) દ્વારા બનતા સમતલના દરેક ભાગને ચરણ અથવા પાદૃ કહે છે.
(iii) આ બે રેખાઓ (x-અક્ષ તથા પુ-અક્ષ) જ્યાં છેદે તે બિંદુને ઉગમબિંદુ કહે છે.
2. નીચેની આકૃતિ જુઓ અને માગ્યા પ્રમાણે જવાબ લખો :
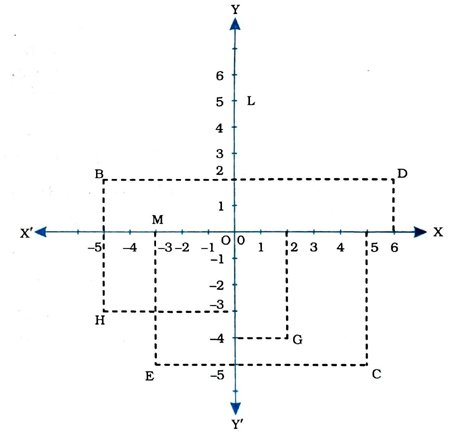
(i) બિંદુ Bના યામ જણાવો.
(ii) બિંદુ Cના યામ જણાવો.
(iii) (– 3, − 5) દ્વારા દર્શાવાતું બિંદુ લખો.
(iv) (2, – 4) દ્વારા દર્શાવાતું બિંદુ લખો.
(v) બિંદુ Dનો ×યામ જણાવો.
(vi) બિંદુ Hનો ઘુમ્યામ જણાવો.
(vii) બિંદુ Lના યામ જણાવો.
(viii) બિંદુ Mના યામ જણાવો.
(i) બિંદુ Bના યામ (– 5, 2) છે.
(ii) બિંદુ Cના યામ (5, – 5) છે.
(iii) (– 3, − 5) દ્વારા દર્શાવાતું બિંદુ E છે.
(iv) (2, 4) દ્વારા દર્શાવાતું બિંદુ ઉ છે.
(v) બિંદુ Dનો x-યામ 6 છે.
(vi) બિંદુ Hનો પુ-યામ -3 છે.
(vii) બિંદુ Lના યામ (0, 5) છે.
(viii) બિંદુ Mના યામ (−3, 0) છે.
સ્વાધ્યાય – 3.3
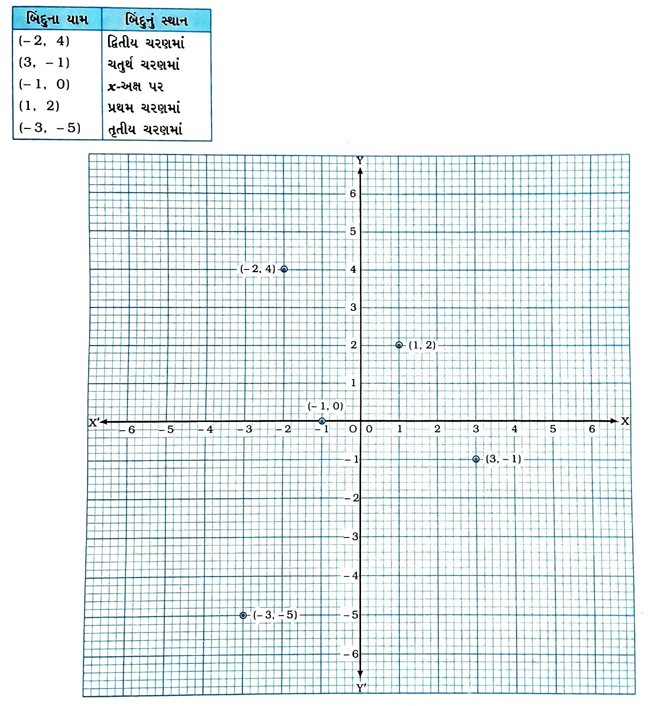
1. કયા ચરણમાં અથવા કયા અક્ષ ઉપર (– 2, 4), (3, – 1), (−1, 0), (1, 2) અને (– 3, – 5) બિંદુઓ છે? તમારા જવાબની ચકાસણી બિંદુઓને યામ-સમતલમાં દર્શાવી કરો.
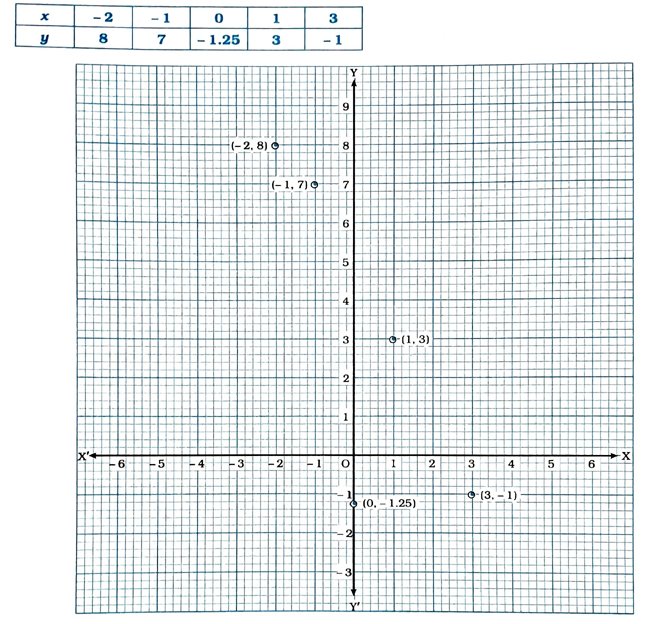
2. નીચેના કોષ્ટકમાંથી સમતલમાં અનુકૂળ સ્કેલમાપના એકમોનું અંતર અક્ષો પર પસંદ કરીને (x, y) બિંદુઓનું નિરૂપણ કરો :
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરોઃ (ફક્ત અંતિમ જવાબ)
( 1 ) ઉગમબિંદુના યામ …… છે.
( 2 ) પુ-અક્ષ પર આવેલ બિંદુનો x-યામ ……. હોય.
( 3 ) Z X’OY’ના અંદરના ભાગને ……. ચરણ કહે છે.
( 4 ) બિંદુ (– 2, 8) એ ……. ચરણમાં છે.
( 5 ) ચતુર્થ ચરણમાં આવેલ બિંદુનો y-યામ …….. હોય.
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) બિંદુ (0, – 18) કયા કિરણ પર આવેલ છે?
( 2 ) જે બિંદુના બંને યામ ઋણ હોય તે બિંદુ કયા ચરણમાં હોય?
( 3 ) m < 0 અને n > 0 હોય, તો બિંદુ (m, n) કયા ચરણમાં હોય?
( 4 ) x-અક્ષ પર આવેલ બિંદુનો કયો યામ શૂન્ય હોય?
( 5 ) બિંદુ (0, 7)નું ઉગમબિંદુથી અંતર શોધો.
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) જો બિંદુ (– 5, a) x-અક્ષ પર આવેલ હોય, તો હની કિંમત ……… છે.
A. 5
B. – 5
C. 25
D. 0
(2) બિંદુ (5/2, – 5/2) એ …… ચણમાં છે.
A. પ્રથમ
B. દ્વિતીય
C. તૃતીય
D. ચતુર્થ
( 3 ) x -અક્ષ બિંદુ …….. માંથી પસાર ન થાય.
A. (7, 0)
B. (0, 3)
C. (–12, 0)
D. (3/4, 0)
( 4 ) જો (a + 3, 7) અને (8, b – 2) સમાન બિંદુઓ દર્શાવતા હોય, તો બિંદુ (a, b) એ ……. ચરણમાં છે,
A. પ્રથમ
B. દ્વિતીય
C. તૃતીય
D, ચતુર્થ
( 5 ) બિંદુ (0, – 12) એ ……. છે.
A. પ્રથમ ચરણમાં
B. તૃતીય ચરણમાં
C. x-અક્ષ પર
D. y-અક્ષ પર
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) બિંદુ (− 7, 2) એ ચતુર્થ ચરણમાં છે.
( 2 ) A ), 7) એ પુ-અક્ષનું બિંદુ છે.
( 3 ) બિંદુઓ P (5, 0) અને (−3, 0) માટે PQ = 8.
( 4 ) બિંદુ (– 5, –8) એ તૃતીય ચરણમાં છે,
( 5 ) a = 5, b = 3, c = ~ 2 અને d = − 5 માટે, બિંદુ (a + c, b + d) એ પ્રથમ ચરણમાં છે.
જવાખો
1. ( 1 ) (0, 0) ( 2 ) 0 ( 3 ) તૃતીય ( 4 ) દ્વિતીય ( 5 ) ઋણ
2. ( 1 ) OY’ ( 2 ) તૃતીય ( 3 ) દ્વિતીય ( 4 ) પુ-યામ ( 5 ) 7
3. ( 1 ) 0 ( 2 ) ચતુર્થ ( 3 ) (0, 3) ( 4 ) પ્રથમ ( 5 ) પુ-અક્ષ પર
4. ( 1 ) ખોટું ( 2 ) ખરું ( 3 ) ખરું ( 4 ) ખરું ( 5 ) ખોટું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here