Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 5 યુક્લિડની ભૂમિતિનો પરિચય
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 5 યુક્લિડની ભૂમિતિનો પરિચય
સ્વાધ્યાય – 5.1
1. નીચે આપેલાં વિધાનોમાંથી કયાં વિધાનો સત્ય છે અને કાં વિધાનો અસત્ય છે? તમારા જવાબ માટે કારણો આપો :
(i) એક બિંદુમાંથી પસાર થતી માત્ર એક રેખા દોરી શકાય છે.
(ii) બે ભિન્ન બિંદુઓમાંથી પસાર થતી અસંખ્ય રેખાઓ હોય છે.
(iii) એક સાન્ત રેખાને બંને તરફ અનિશ્ચિત રીતે લંબાવી શકાય છે.
(iv) જો બે વર્તુળ સમાન છે, તો તેમની ત્રિજ્યાઓ સમાન હોય છે.
(v) નીચેની આકૃતિમાં જો AB = PQ અને PQ = XY છે, તો AB = XY થાય.
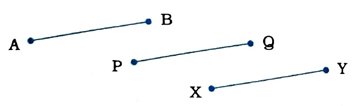
(i) આપેલ વિધાન અસત્ય છે, કારણ કે એક બિંદુમાંથી પસાર થતી હોય તેવી અસંખ્ય રેખાઓ દોરી શકાય. તેના સૌથી સરળ ઉદાહરણ તરીકે પરસ્પર છેદતી રેખાઓ અથવા પરસ્પર લંબ રેખાઓ લઈ શકાય. અહીં, બે રેખાઓના અનન્ય છેદબિંદુમાંથી બે રેખાઓ પસાર થાય છે.
(ii) આપેલ વિધાન અસત્ય છે, કારણ કે જો તેવું હોય તો બે બિંદુ વચ્ચેનું અંતર કદી વ્યાખ્યાયિત ન કરી શકાય. વળી તે પૂર્વધારણા 1નો વિરોધાભાસ કરે છે.
(iii) આપેલ વિધાન પૂર્વધારણા 2 અનુસાર સત્ય છે.
(iv) આપેલ વિધાન સત્ય છે. જો બે વર્તુળો સમાન હોય તો તેમના પરિઘ અને કેન્દ્ર એકબીજાને બંધબેસતા થાય. હવે, ત્રિજ્યા એ કેન્દ્ર અને પરિઘના કોઈ પણ બિંદુ વચ્ચેનું અંતર હોવાથી તે વર્તુળોની ત્રિજ્યાઓ પણ સમાન હોય.
(v) આપેલ વિધાન સ્વયંસિદ્ધ સત્ય 1 અનુસાર સત્ય છે. અહીં AB અને XY એક જ વસ્તુ PQને સમાન હોવાથી AB અને XY પણ સમાન થાય. એટલે કે AB = XY.
2. નીચે આપેલાં પદોની વ્યાખ્યા આપો. શું તેના માટે કોઈ એવાં પદ છે જેને વ્યાખ્યાયિત કરવાની જરૂર છે? એ કયાં છે? અને તમે તેને કેવી રીતે વ્યાખ્યાયિત કરશો?
(i) સમાંતર રેખાઓ
(ii) લંબરેખાઓ
(iii) રેખાખંડ
(iv) વર્તુળની ત્રિજ્યા
(v) ચોરસ
(i) સમાંતર રેખાઓ : એક જ સમતલમાં આવેલી બે રેખાઓ પરસ્પર છેદે નહીં તો તેમને સમાંતર રેખાઓ કહેવાય.
(ii) લંબરેખાઓ : જે બે રેખાઓ પરસ્પર કાટખૂણે છેદે તેમને લંબરેખાઓ કહેવાય.
(iii) રેખાખંડ : રેખાના એવા ભાગને રેખાખંડ કહે છે, જેને બે અંત્યબિંદુઓ હોય.
(iv) વર્તુળની ત્રિજ્યા : વર્તુળના કેન્દ્ર અને પરિઘ પરના કોઈ પણ બિંદુને જોડતા રેખાખંડને વર્તુળની ત્રિજ્યા કહેવાય.
નોંધ : વર્તુળની ત્રિજ્યાના માપને પણ વર્તુળની ત્રિજ્યા કહેવામાં આવે છે.
(v) ચોરસ : જેની ચારેય બાજુઓ એકરૂપ હોય તથા ચારેય ખૂણા એકરૂપ હોય તેવા ચતુષ્કોણને ચોરસ કહેવાય.
અહીં રેખા, સમતલ, કાટખૂણો, વર્તુળનું કેન્દ્ર, પરિઘ અને ચતુષ્કોણ જેવાં પદો છે જેને વ્યાખ્યાયિત કરવાની જરૂર છે. તે પૈકીના રેખા અને સમતલને વ્યાખ્યાયિત ન કરી શકાય કારણ કે તે અવ્યાખ્યાયિત પદો છે. બાકીનાં ચાર પદોની વ્યાખ્યા નીચે મુજબ આપી શકાય :
(i) કાટખૂણો : 90° માપવાળા ખૂણાને કાટખૂણો કહે છે.
(ii) વર્તુળનું કેન્દ્ર : વર્તુળના સમતલમાં આવેલું એવું બિંદુ કે જે વર્તુળના દરેક બિંદુથી સમાન અંતરે હોય તેને વર્તુળનું કેન્દ્ર કહે છે.
(iii) પરિઘ : વર્તુળની પરિમિતિને પરિઘ કહે છે.
(iv) ચતુષ્કોણ : એક જ સમતલમાં આવેલ બંધ આકૃતિ કે જેને ચાર બાજુ અને ચાર ખૂણા હોય તેને ચતુષ્કોણ કહે છે.
3. નીચે આપેલ બે પૂર્વધારણાઓનો વિચાર કરો :
(i) જો બે ભિન્ન બિંદુ A અને B આપ્યાં હોય, તો તેમની વચ્ચે હોય તેવું એક બિંદુ C મળે.
(ii) એક રેખા પર ન આવેલાં હોય તેવા ઓછાંમાં ઓછાં ત્રણ બિંદુઓ મળે.
શું આ પૂર્વધારણાઓમાં કોઈ અવ્યાખ્યાયિત પદ છે? શું આ પૂર્વધારણાઓ સુસંગત છે? શું આ પૂર્વધારણાઓ યુક્લિડની પૂર્વધારણામાંથી મળે છે? સ્પષ્ટ કરો.
હા. આ પૂર્વધારણાઓમાં બે અવ્યાખ્યાયિત પદ – બિંદુ અને રેખા આવેલ છે.
હા. આ પૂર્વધારણાઓ સુસંગત છે.
પૂર્વધારણા (i) દર્શાવે છે કે આપેલ બે ભિન્ન બિંદુઓ A અને B માટે એવું એક બિંદુ C મળે જે રેખા AB ૫૨ A અને Bની વચ્ચે હોય.
પૂર્વધારણા (ii) દર્શાવે છે કે આપેલ બે ભિન્ન બિંદુઓ A અને B માટે એવું ઓછામાં ઓછું એક બિંદુ C તો મળે જ જે રેખા AB ૫૨ ન હોય.
આ પૂર્વધારણાઓ યુક્લિડની પૂર્વધારણામાંથી નહીં, પરંતુ પૂર્વધારણા 5.1માંથી મળે છે.
4. જો AC = BC થાય તેવું બિંદુ C બિંદુઓ A અને Bની વચ્ચે હોય, તો સાબિત કરો કે AC = 1/2 AB છે. આકૃતિ દોરીને તેને સ્પષ્ટ કરો.

5. પ્રશ્ન 4માં બિંદુ C રેખાખંડ ABનું એક મધ્યબિંદુ કહેવાય છે. સાબિત કરો કે, દરેક રેખાખંડને એક અને માત્ર એક જ મધ્યબિંદુ હોય.
પ્રશ્ન 4માંથી આપણને રેખાખંડ ABના મધ્યબિંદુ Cના બે ગુણધર્મો મળે છે : (i) બિંદુ C એ રેખાખંડ AB ૫૨ A અને Bની વચ્ચે આવેલ છે. (ii) C એ A અને Bથી સમાન અંતરે છે.
શક્ય હોય તો ધારો કે, બિંદુ D તથા બિંદુ C ભિન્ન બિંદુઓ છે અને D એ રેખાખંડ ABનું મધ્યબિંદુ છે.
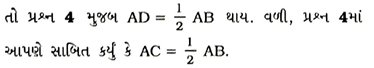
∴ AD = AC [સ્વયંસિદ્ધ સત્ય 1]
હવે, D અને C બંને રેખાખંડ AB ૫૨ A અને Bની વચ્ચે છે તથા બંને હિંદુઓ Aથી સમાન અંતરે છે. આ પરથી સાબિત થાય છે કે D અને C સમાન બિંદુઓ છે, ભિન્ન નથી. આમ, દરેક રેખાખંડને એક અને માત્ર એક જ મધ્યબિંદુ હોય.
6. આપેલ આકૃતિમાં જો AC = BD હોય, તો સાબિત કરો કે AB = CD છે.
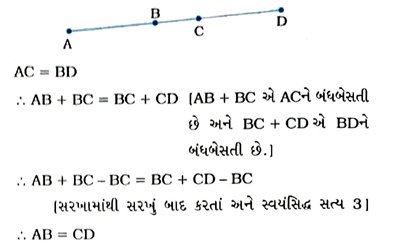
7. યુક્લિડનાં સ્વયંસિદ્ધ સત્યોની યાદીમાં આપેલ સ્વયંસિદ્ધ સત્ય 5 એક સનાતન સત્ય કેમ માનવામાં આવે છે? (યાદ રાખો કે આ પ્રશ્ન પાંચમી પૂર્વધારણા સાથે સંબંધિત નથી.)
સ્વયંસિદ્ધ સત્ય 5 દર્શાવે છે કે આખું તેના ભાગ કરતાં મોટું હોય છે. શબ્દ ભાગનો અર્થ જ આખા કરતાં કાંઈક ઓછા માટે થાય છે. આ હકીકત કોઈ પણ વસ્તુ તથા દુનિયાના કોઈ પણ ભાગમાં સાચી છે. આથી તેને સનાતન સત્ય માનવામાં આવે છે.
દઢીકરણ માટેના દાખલા
1. આપેલ આકૃતિમાં જો AB = CD હોય, તો સાબિત કરો કે AC = BD. આપની સાબિતીમાં વાપરેલ સ્વયંસિદ્ધ સત્યો જણાવો.
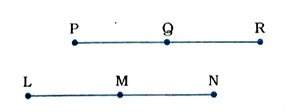
2. આપેલ આકૃતિમાં PQ = LM, Q એ PRનું મધ્યબિંદુ તથા M એ LNનું મધ્યબિંદુ છે. સ્વયંસિદ્ધ સત્યોના ઉપયોગથી સાબિત કરો કે PR = LN.
સ્વાધ્યાય – 5.2
1. તમે યુક્લિડની પાંચમી પૂર્વધારણાને સરળતાથી સમજી શકાય તેમ કેવી રીતે લખી શકશો?
જો કોઈ બે રેખાઓ m અને nને ત્રીજી રેખા l ભિન્ન બિંદુઓમાં છેદે, તો ચાર અંતઃકોણો મળે. જો આ ચાર અંતઃકોણો પૈકી રેખા l ની કોઈ પણ એક જ બાજુ પર આવેલા બે અંતઃકોણોનો સરવાળો 180° થાય, તો રેખાઓ m અને n એકબીજાને છેદે નહીં, એટલે કે m અને n સમાંતર રેખાઓ છે.
2. શું યુક્લિડની પાંચમી પૂર્વધારણા પરથી સમાંતર રેખાઓનું અસ્તિત્વ નક્કી થાય છે? સ્પષ્ટ કરો.
હા. યુક્લિડની પાંચમી પૂર્વધારણા પરથી સમાંતર રેખાઓનું અસ્તિત્વ નક્કી થાય છે. જો કોઈ રેખા l બે રેખાઓ m અને nને એવી રીતે છેદે કે જેથી રેખા l ની એક તરફના અંતઃકોણોનો સરવાળો બે કાટખૂણા જેટલો, એટલે કે 180° થાય, તો તે રેખાઓ m અને n રેખા l ની તે બાજુએ છેદશે નહીં. આમ હોય, તો l ની બીજી તરફના બે અંતઃકોણોનો સરવાળો પણ બે કાટખૂણા જેટલો જ થાય અને તેથી m અને n રેખા l ની બીજી તરફ પણ છેદશે નહીં. આમ, l ની એક જ તરફના બે અંતઃકોણોનો સરવાળો 180° થાય, તો m અને n કદી છેદશે નહીં. આ રીતે m અને n સમાંતર રેખાઓ બને.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરોઃ (ફક્ત અંતિમ જવાબ)
( 1 ) જે વિધાન સાબિત કરવામાં આવે તેને ……. કહે છે.
( 2 ) શ્રીયંત્ર એ અંદરોઅંદર ગૂંથાયેલા નવ …….. ત્રિકોણનું સંયોજન છે.
( 3 ) પ્રાચીન ભારતમાં ભૌમિતિક રચનાઓ માટેનો મહત્ત્વપૂર્ણ ગ્રંથ …….. હતો.
( 4 ) રેખા એ …….. વગરની લંબાઈ છે.
( 5 ) સિંધુખીણની સંસ્કૃતિમાં વપરાતી ઈંટોમાં લંબાઈ, પહોળાઈ અને જાડાઈનો ગુણોત્તર ……. હતો.
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) ઘનને કેટલા પરિમાણ હોય છે?
( 2 ) શ્રીયંત્રમાં કેટલા ઉપત્રિકોણ બને છે?
( 3 ) સમતલને કેટલા પરિમાણ હોય છે?
( 4 ) થેલ્સ કયા દેશનો વતની હતો?
( 5 ) બિંદુને કેટલા પરિમાણ હોય છે?
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) Elementsના પુસ્તક 1માં ……… વ્યાખ્યાઓ આપેલ છે.
A. 43
B. 9
C. 23
D. 13
( 2 ) ઘન – સમતલ – રેખા – બિંદુ સુધીનાં ચરણોમાં દરેક ચરણમાં એક પરિમાણ ……. જાય છે.
A. વધતું
B. ઘટતું
C. ઉમેરાતું
D. નવું આવતું
( 3 ) સૌપ્રથમ જ્ઞાત સાબિતી ગણિતશાસ્ત્રી …….. આપી.
A. પાયથાગોરસે
B. યુક્લિડે
C. આર્યભટ્ટે
D. થેલ્સે
( 4 ) યુક્લિડે તેના પ્રસિદ્ધ ગ્રંથ Elementsનું …….. પ્રકરણોમાં વિભાજન કર્યું હતું.
A. 9
B. 13
C. 21
D. 15
( 5 ) પ્રાચીન ભારતમાં ગૃહસ્થ કર્મકાંડ માટે ……… વેદીઓનો ઉપયોગ થતો હતો.
A. ચોરસ અને વર્તુળાકાર
B. ત્રિકોણ અને લંબચોરસ
C. સમાંતરબાજુ ચતુષ્કોણ અને ત્રિકોણ
D. ત્રિકોણ અને ચોરસ
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) બે ભિન્ન બિંદુઓમાંથી પસાર થતી અસંખ્ય રેખાઓ મળે.
( 2 ) સરખી વસ્તુઓના બમણા એકબીજાને સમાન હોય છે.
( 3 ) યુક્લિડ એ થેલ્સનો ખ્યાતનામ વિદ્યાર્થી હતો.
( 4 ) એક બિંદુમાંથી ફક્ત એક જ રેખા પસાર થાય.
( 5 ) બે ભિન્ન રેખાઓમાં એકથી વધુ બિંદુ સામાન્ય ન હોય.
જવાબો
1. ( 1 ) પ્રમેય ( 2 ) સમઢિબાજુ ( 3 ) સૂલબાસૂત્ર ( 4 ) પહોળાઈ ( 5 ) 4 : 2 : 1
2. ( 1 ) ત્રણ ( 2 ) 43 ( 3 ) બે ( 4 ) ગ્રીસ ( 5 ) શૂન્ય
3. ( 1 ) 23 ( 2 ) ઘટતું ( 3 ) થેલ્સે ( 4 ) 13 ( 5 ) ચોરસ અને વર્તુળાકાર
4. ( 1 ) ખોટું ( 2 ) ખરું ( 3 ) ખોટું ( 4 ) ખોટું ( 5 ) ખરું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here