Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 6 રેખાઓ અને ખુણાઓ
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 6 રેખાઓ અને ખુણાઓ
સ્વાધ્યાય – 6.1
1. આપેલ આકૃતિમાં રેખા AB અને CD, Oમાં છેદે છે. જો ∠AOC + ∠BOE = 70° અને ∠BOD = 40°, તો / ∠BOE અને વિપરીત ∠COE મેળવો.


2. આપેલ આકૃતિમાં રેખા XY અને MIN, Oમાં છેદે છે. જો ∠POY = 90° અને a : b = 2 : 3, તો c શોધો.
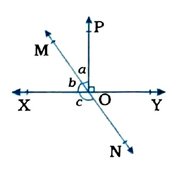

∴ 54° + c = 180°
∴ c = 180° – 54°
∴ c = 126°
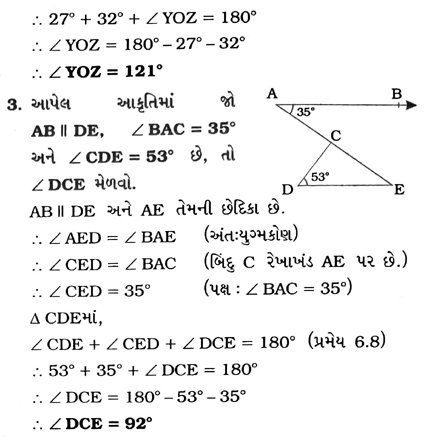
3. આપેલ આકૃતિમાં ∠PQR = ∠PRQ, તો સાબિત કરો કે ∠PQS = ∠PRT.

4. આપેલ આકૃતિમાં જો x + y = w + z હોય, તો સાબિત કરો કે AOB રેખા છે.
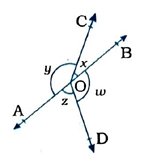
આપણે જાણીએ છીએ કે એક બિંદુ પર બનતાં બધા જ ખૂણાઓનો સરવાળો 360° થાય છે.
∴ x + y + z + w = 360°
∴ x + y + x + y = 360° (પક્ષ : x + y = w + z)
∴ 2 (x + y) = 360º
∴ x + y = 180°
∴ ∠COB + ∠COA = 180°
પરંતુ, ∠COB અને ∠COA આસન્નકોણ છે અને તેમનો સરવાળો 180° થાય છે.
માટે, પૂર્વધારણા 6.2 મુજબ AOB રેખા છે.
5. આપેલ આકૃતિમાં POQ રેખા છે. કિરણ OR રેખા PQને લંબ છે. કિરણ OP અને OR વચ્ચે અન્ય એક કિરણ OS આવેલ છે. સાબિત કરો કે,
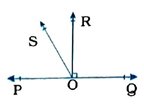
∠ROS = 1/2 (∠QOS – ∠POS).
કિરણ OR રેખા PQને લંબ છે.
∴ ∠QOR = ∠POR = 90°
∠QOR અને ∠ROS આસન્નકોણ છે, જેમાં કિરણ OR સામાન્ય ભુજ છે.
∴ ∠QOS = ∠QOR + ∠ROS
∴ ∠QOS = 90° + ∠ROS …… (1)
તે જ રીતે ∠POS અને ∠ROS આસકોણ છે, જેમાં કિરણ OS સામાન્ય ભુજ છે.
∴ ∠POR = ∠POS + ∠ROS
∴ 90° = ∠POS + ∠ROS
∴ ∠POS = 90° – ∠ROS ……. (2)
હવે, (1)માંથી (2)ની બાદબાકી કરતાં,
∠QOS – ∠POS (90° + ∠ROS) – (90° – ∠ROS)
∴ ∠QOS – ∠POS = 90° + ∠ROS – 90° + ∠ROS
∴ ∠QOS – ∠POS = 2 ∠ROS
∴ ∠ROS = 1/2 (∠QOS – ∠POS)
6. ∠XYZ = 64° આપેલ છે અને XYને બિંદુ P સુધી લંબાવેલ છે. આપેલ સૂચના પરથી આકૃતિ દોરો. જો કિરણ YQ, ∠ZYPનો દ્વિભાજક હોય, તો ∠XYQ અને વિપરીત ∠QYPનું માપ શોધો.

સ્વાધ્યાય – 6.2
1. આપેલ આકૃતિમાં x અને ઘુનાં માપ શોધો અને બતાવો કે AB || CD છે.

(1) અને (2) પરથી x = y મળે. પરંતુ, આ ખૂણાઓ રેખાઓ AB અને CDની છેદિકા PS દ્વારા બનતા અંતઃયુગ્મકોણ છે અને તેઓ સમાન છે.
આથી AB || CD.
2. આપેલ આકૃતિમાં જો AB || CD, CD || EF અને y : z = 3 : 7 છે, તો xનું માપ શોધો.
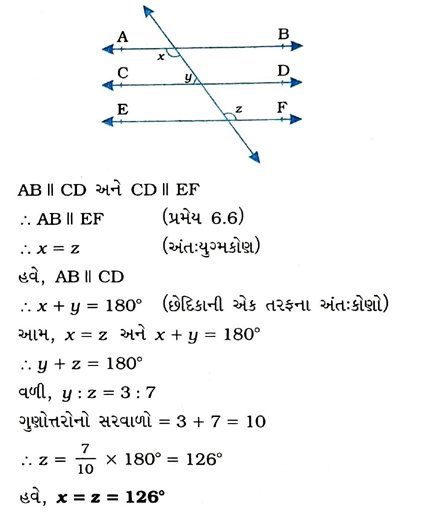
3. આપેલ આકૃતિમાં જો AB || CD, EF ⊥ CD અને ∠GED = 126° છે, તો ∠AGE, ∠GEF અને ∠FGE મેળવો.

અહીં, AB || CD અને GE છેદિકા છે.
∴ ∠AGE અને ∠GED સમાન અંતયુગ્મકોશ છે.
∴ ∠GED = ∠AGE
∴ ∠AGE = 126° (પક્ષ : ∠GED=126°)
હવે, EF ⊥ CD
∴ ∠FED = 90°
∠GEF + ∠FED = ∠GED (આસન્નકોણ)
∴ ∠GEF + 90° = 126°
∴ ∠GEF = 36°
હવે, ∠AGE + ∠FGE = 180° (રેખિક જોડના ખૂણા)
∴ 126° + ∠FGE = 180°
∴ ∠FGE = 180° – 126°
∴ ∠FGE = 54°
4. આપેલ આકૃતિમાં જો PQ || ST, ∠PQR = 110° અને ∠RST = 130°, તો ∠QRS મેળવો.
સૂિચન : બિંદુ Rમાંથી પસાર થતી STને સમાંતર એક રેખા દોરો.]
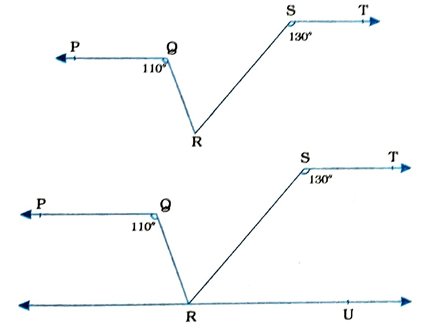
રચના : Rમાંથી પસાર થતી STને સમાંતર રેખા RU દોરો,

∴ ∠QRS + ∠SRU = ∠QRU
∴ ∠QRS + 50° = 110° [(1) અને (2) મુજબ)
∴ ∠QRS = 60°
5. આપેલ આકૃતિમાં જો AB || CD, ∠APQ= 50° અને ∠PRD = 127° છે, તો x અને y મેળવો.

6. આપેલ આકૃતિમાં PQ અને RS બે અરીસા છે. તે બંને એકબીજાને સમાંતર રાખેલા છે.
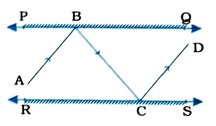
એક આપાતિકરણ AB અરીસા PQને B પર અથડાય છે અને પરાવર્તિત કિરણ માર્ગ BC પર ચાલીને અરીસા RSને C પર અથડાય છે તથા ફરી CD પર પરાવર્તિત થઈ જાય છે. સાબિત કરો કે, AB || CD છે.
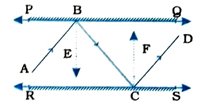
રચના : રેખા PQને લંબ કિરણ BE દોરો તથા રેખા RSને લંબ કિરણ CF દોરો.
આપણે જાણીએ છીએ કે સાદા અરીસા માટે આપાતકોણ = પરાવર્તન કોણ.
આથી બિંદુ B આગળ ∠ABE = ∠EBC ….. … (1)
અને બિંદુ C આગળ ∠BCF = ∠FCD …… … (2)
હવે, PQ || RS, BE ⊥ PQ અને CF ⊥ RS છે.
∴ BE || CF
∴ ∠EBC = ∠BCF (અંતઃયુગ્મકોણ) ……. (3)
(1), (2) અને (3) પરથી,
∠ABE = ∠EBC = ∠BCF = ∠FCD
∴ ∠ABE + ∠EBC = ∠BCF + ∠FCD
∴ ∠ABC = ∠BCD (આસન્નકોણ)
પરંતુ, ∠ABC અને ∠BCD એ રેખાઓ AB અને CDની છેદિકા BC દ્વારા બનતા અંતઃયુગ્મકોણ છે અને તેઓ સમાન છે.
∴ AB || CD
સ્વાધ્યાય – 6.3
1. આપેલ આકૃતિમાં Δ PQRની બાજુઓ QP અને RQને અનુક્રમે બિંદુઓ S અને T સુધી લંબાવેલ છે. જો ∠SPR = 135° હોય અને ∠PQT = 110° હોય, તો ∠PRQ મેળવો.

અહીં, ∠SPR અને ∠PQT બંને Δ PQRના બહિષ્કોણ છે. આથી પ્રમેય 6.8 મુજબ,
∠SPR = ∠PQR + ∠PRQ અને
∠PQT = ∠QPR + ∠PRQ
∴ ∠PQR + ∠PRQ = 135° અને
∠QPR + ∠PRQ = 110°
બંને સમીકરણોનો સરવાળો લેતાં,
∠PQR + ∠PRQ + ∠QPR + ∠PRQ = 135° + 110°
∴ 180° + ∠PRQ = 245° (પ્રમેય 6.7)
∴ ∠PRQ = 245° – 180°
∴ ∠PRQ = 65°
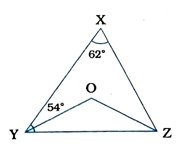
2. આપેલ આકૃતિમાં ∠X = 62° અને ∠XYZ = 54° છે. જો Δ XYZના ∠XYZ અને ∠XZYના દ્વિભાજક અનુક્રમે YO અને ZO હોય, તો ∠OZY અને ∠YOZ મેળવો.

4. આપેલ આકૃતિમાં જો રેખાઓ PQ અને RS બિંદુ T પર એ પ્રકારે છેદે છે. કે ∠PRT = 40°, ∠RPT = 95° અને ∠TSQ = 75° છે, તો ∠SQT મેળવો.



હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરોઃ (ફક્ત અંતિમ જવાબ)
( 1 ) રેખિક જોડના ખૂણાઓનો સરવાળો ……. થાય.
( 2 ) ત્રિકોણના કુલ ……. બહિષ્કોણ મળે.
( 3 ) જે બે ખૂણાઓનો સરવાળો 90° થાય તે ખૂણાઓને એકબીજાના …….. કહે છે.
( 4 ) વિપરીતકોણનું માપ ………ની વચ્ચે હોય.
( 5 ) જે બે ખૂણાઓનો સરવાળો 180॰ થાય તે ખૂણાઓને એક્બીજાના ……. કહે છે.
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) 85ના માપના ખૂણાના પૂરકકોણનું માપ શોધો.
( 2 ) 37ના માપના ખૂણાના કોટિકોણનું માપ શોધો.
( 3 ) જો રૈખિક જોડના બે ખૂણાનાં માપ 7 : 8ના પ્રમાણમાં હોય, તો તે પૈકી મોટા ખૂણાનું માપ શોધો.
( 4 ) બે પૂરકકોણના માપ x + 20° અને 2x + 10° હોય, તો તે પૈકી મોટા ખૂણાનું માપ શોધો.
( 5 ) 38ના ખૂણાના કોટિકોણના પૂરકકોણનું માપ શોધો.
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) 65ના માપના ખૂણાના પૂરકકોણનું માપ …….. છે.
A. 35°
B. 25°
C. 115°
D. 125°
( 2 ) બે પૂરકકોણના માપનો તફાવત 38॰ છે, તો તેમાંના લઘુકોણનું માપ ……. છે.
A. 52°
B. 71°
C. 26°
D. 61°
( 3 ) Δ ABCમાં ∠A = 85° અને ∠B = 75° હોય, તો ∠C = ……. .
A. 30°
B. 20°
C. 50°
D. 75°
( 4 ) ∠ACD એ A ABCનો બહિષ્કોણ છે. જો ∠A = 65° અને ∠ACD = 120° હોય, તો ∠B = ……..
A. 65°
B. 45°
C. 55°
D. 35°
( 5 ) Δ PQRમાં ∠P : ∠Q : ∠R = 3 : 7 : 5 હોય, તો ∠R = ……… .
A. 36°
B. 84°
C. 60°
D. 120°
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) 75ના ખૂણાના પૂરકકોણનું માપ 15॰ છે.
( 2 ) ત્રિકોણનાં બે જુદાં જુદાં શિરોબિંદુઓ પર મળતા બહિષ્કોણો લઘુકોણ હોઈ શકે.
( 3 ) 40°ના ખૂણાના કોટિકોણના પૂરકકોણનું માપ 130° છે.
( 4 ) Δ ABCમાં ∠A = 50°, ∠B = 50° અને ∠C = 80° છે. જો ∠ACD એ Δ ABCનો બહિષ્કોણ હોય, તો ∠ACD = 100°.
( 5 ) 72ના ખૂણાના કોટિકોણનું માપ 108॰ છે.
જવાબો
1. ( 1 ) 180° ( 2 ) છ ( 3 ) કોટિકોણ ( 4 ) 180° અને 360° ( 5 ) પૂરકકોણ
2. (1) 95° (2) 53° (3) 96° (4) 110° (5) 128°
3. (1) 115° (2) 71° (3) 20° (4) 55° (5) 60°
4. ( 1 ) ખોટું ( 2 ) ખોટું ( 3 ) ખરું ( 4 ) ખરું ( 5 ) ખોટું
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here