Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 9 સમાંતરબાજુ ચતુષ્કોણ અને ત્રિકોણનાં ક્ષેત્રફળ
Gujarat Board | Class 9Th | Model Question Paper & Solution | Mathematics | Chapter – 9 સમાંતરબાજુ ચતુષ્કોણ અને ત્રિકોણનાં ક્ષેત્રફળ
સ્વાધ્યાય – 9.1
1. નીચેની આકૃતિઓમાં એક જ સમાન પાયા પર અને સમાંતર રેખાની એક જોડની રેખાઓ વચ્ચે કઈ આકૃતિઓ આવેલી છે? શક્ય હોય તેવા કિસ્સામાં સામાન્ય પાયો અને સમાંતર રેખાઓ જણાવો.

( 1 ) આકૃતિ ( i )માં સમલંબ ચતુષ્કોણ ABCD અને Δ PDC એક જ પાયા પર અને સમાંતર રેખાઓની એક જ જોડ વચ્ચે આવેલ આકૃતિઓ છે.
અહીં, એક જ પાયો DC છે તથા DC અને AB સમાંતર છે.
( 2 ) આકૃતિ (ii )માં કોઈ પણ બે આકૃતિઓ એક જ પાયા પર અને સમાંતર રેખાઓની એક જ જોડ વચ્ચે આવેલ નથી.
( 3 ) આકૃતિ (11)માં સમાંતરબાજુ ચતુષ્કોણ PQRS અને Δ TQR એક જ પાયા પર અને સમાંતર રેખાઓની એક જ જોડ વચ્ચે આવેલ આકૃતિઓ છે.
અહીં, એક જ પાયો QR છે તથા QR અને PS સમાંતર છે.
( 4 ) આકૃતિ ( iv )માં કોઈ પણ બે આકૃતિઓ એક જ પાયા પર અને સમાંતર રેખાઓની એક જ જોડ વચ્ચે આવેલ નથી.
( 5 ) આકૃતિ ( ૪ )માં સમાંતરબાજુ ચતુષ્કોણો ABCD તથા APQD અને સમલંબ ચતુષ્કોણો ABQD તથા APCD એક જ પાયા પર અને સમાંતર રેખાઓની એક જ જોડ વચ્ચે આવેલ આકૃતિઓ છે.
અહીં, એક જ પાયો AD છે તથા AD અને BQ સમાંતર છે.
( 6 ) આકૃતિ (vi)માં કોઈ પણ બે આકૃતિઓ એક જ પાયા પર અને સમાંતર રેખાઓની એક જ જોડ વચ્ચે આવેલ નથી.
સ્વાધ્યાય – 9.2
1. આપેલ આકૃતિમાં ABCD એક સમાંતરબાજુ ચતુષ્કોણ છે. AE ⊥ DC અને CF ⊥ AD છે. જો AB = 16 સેમી, AE = 8 સેમી અને CF = 10 સેમી, તો AD શોધો.

2. જો E, F, G અને H એ અનુક્રમે સમાંતરબાજુ ચતુષ્કોણ ABCDની બાજુઓનાં મધ્યબિંદુઓ હોય, તો સાબિત કરો કે ar(EFGH) = 1/2 ar (ABCD).
સમાંતરબાજુ ચતુષ્કોણ ABCDની બાજુઓ AB, BC, CD અને DAનાં મધ્યબિંદુઓ અનુક્રમે E,F, G અને H છે. GE દોરો.


3. સમાંતરબાજુ ચતુષ્કોણ ABCDની બાજુઓ DC અને AD પર અનુક્રમે બિંદુઓ P અને Q આવેલાં છે, તો ar (APB) = ar (BQC) થાય તેમ સાબિત કરો.
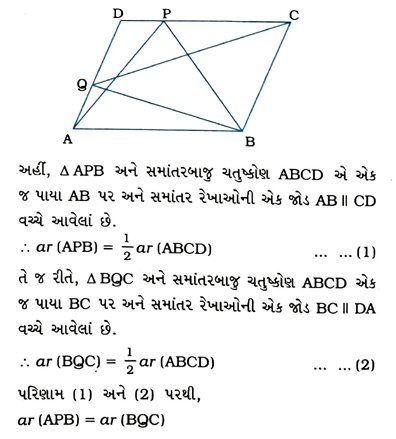
4. આપેલ આકૃતિમાં P એ સમાંતરબાજુ ચતુષ્કોણ ABCDના અંદરના ભાગમાં આવેલું કોઈ બિંદુ છે, તો સાબિત કરો કે

5. આપેલ આકૃતિમાં PQRS અને ABRS સમાંતરબાજુ ચતુષ્કોણ છે તથા બિંદુ X એ બાજુ BR પર આવેલું બિંદુ છે, તો સાબિત કરો કે,

સમાંતરબાજુ ચતુષ્કોણ PQRS અને ABRS એક જ પાયા RS પર અને સમાંતર રેખાની એક જોડ PB || SR વચ્ચે આવેલાં છે.
∴ ar (PQRS) = ar (ABRS) … … (1) …… પરિણામ (i)
Δ AXS અને સમાંતરબાજુ ચતુષ્કોણ ABRS એક જ પાયા AS પર અને સમાંતર રેખાઓની એક જોડ AS || BR વચ્ચે આવેલાં છે.

6. એક ખેડૂત પાસે સમાંતરબાજુ ચતુષ્કોણ PQRS આકારનું એક ખેતર હતું. તેણે RS પર એક બિંદુ A લીધું અને તેને P અને Q સાથે જોડી દીધું. તો ખેતર કેટલા ભાગમાં વહેંચાય છે? આ ભાગોનો આકાર કેવો છે? આ ખેડૂત ખેતરમાં ઘઉં અને કઠોળ સમાન ભાગમાં અને જુદા જુદા ઉગાડવા માંગે છે. તેણે આ કાર્ય કેવી રીતે કરવું જોઈએ?
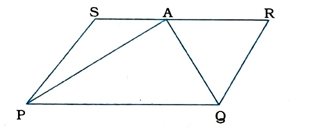
સમાંતરબાજુ ચતુષ્કોણ PQRS આકારના ખેતરની બાજુ RS પરના બિંદુ Aને P અને Q સાથે જોડવાથી ખેતર ત્રણ ભાગમાં વહેંચાય છે. આ ત્રણેય ભાગનો આકાર ત્રિકોણ છે. આ આકારો Δ PSA, Δ APQ અને Δ QRA છે.
અહીં, Δ APQ અને સમાંતરબાજુ ચતુષ્કોણ PQRS એક જ પાયા PQ પર અને સમાંતર રેખાઓની એક જોડ PQ || SRની વચ્ચે આવેલા છે.

ખેડૂત ખેતરમાં ઘઉં અને કઠોળ સમાન ભાગમાં (વિસ્તારમાં) જુદા જુદા ઉગાડવા માંગતો હોય તો તેની પાસે નીચે મુજબના બે વિકલ્પ છે :
( 1 ) Δ APQમાં ઘઉં ઉગાડે તથા Δ PSA અને A QRAમાં કઠોળ ઉગાડે.
( 2 ) Δ APOમાં કઠોળ ઉગાડે તથા Δ PSA અને A QRAમાં ઘઉં ઉગાડે.
સ્વાધ્યાય – 9.3
1. આપેલ આકૃતિમાં Δ ABCની એક મધ્યગા AD પર કોઇ પણ બિંદુ દ છે, તો સાબિત કરો કે ar (ABE) = ar (ACE).
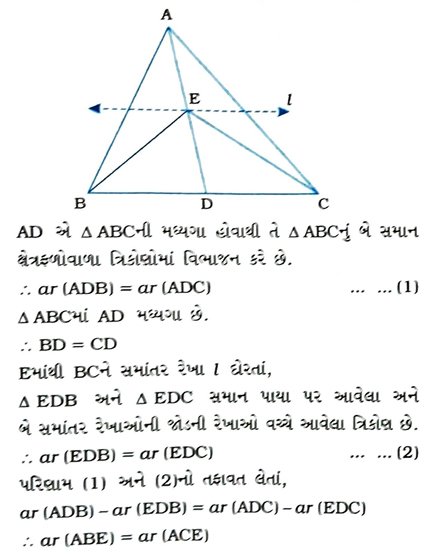
2. ABCમાં મધ્યગા ADનું મધ્યબિંદુ E હોય, તો ar (BED) = 1/4 ar (ABC) થાય તેમ સાબિત કરો.

3. સાબિત કરો કે, સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો તેને સમાન ક્ષેત્રફળવાળા ચાર ત્રિકોણમાં વિભાજિત કરે છે.
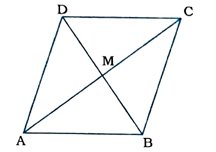
સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો પરસ્પર દુભાગે છે.
આથી સમાંતરબાજુ ચતુષ્કોણ ABCDના વિકર્ણો AC અને BDનું છેદબિંદુ M એ ACનું તેમજ BDનું મધ્યબિંદુ છે.
આથી Δ ABCમાં BM મધ્યગા છે.
∴ ar (ABM) = ar (CBM) ….. (1)
Δ BCDમાં CM મધ્યગા છે.
∴ ar (CBM) = ar (CDM) ….. (2)
Δ ABDમાં AM મધ્યગા છે.
∴ ar (ABM) = ar (DAM) ….. (3)
(1), (2) અને (૩) પરથી,
ar (ABM) = ar (CBM) = ar (CDM) = ar (DAM)
આમ, સમાંતરબાજુ ચતુષ્કોણના વિકર્ણો તેને સમાન ક્ષેત્રફળવાળા ચાર ત્રિકોણોમાં વિભાજિત કરે છે.
4. આપેલ આકૃતિમાં બે ત્રિકોણ ABC અને ABD સમાન પાયા AB પર આવેલા છે. જો AB એ રેખાખંડ CDને O બિંદુએ દુભાગે, તો સાબિત કરો કે ar (ABC) = ar (ABD).

Aમાંથી CDને સમાંતર રેખા દોરવાથી Δ AOC અને Δ AOD સમાન પાયા પર અને બે સમાંતર રેખાઓની જોડ વચ્ચે આવેલા ત્રિકોણ છે.
∴ ar (AOC) = ar (AOD) … (1)
તે જ રીતે, Bમાંથી CDને સમાંતર રેખા દોરવાથી Δ BOC અને Δ BOD સમાન પાયા પર અને બે સમાંતર રેખાઓની જોડ વચ્ચે આવેલા ત્રિકોણ છે.
∴ ar (BOC) = ar (BOD) …. (2)
પરિણામ (1) અને (2)નો સરવાળો લેતાં,
ar (AOC) + ar (BOC) = ar (AOD) + ar (BOD)
∴ ar (ABC) = ar (ABD)
5. Δ ABCની બાજુઓ BC, CA અને ABનાં મધ્યબિંદુઓ અનુક્રમે D, E અને F છે, તો સાબિત કરો કે

6. આપેલ આકૃતિમાં ચતુષ્કોણ ABCDના વિકર્ણો AC અને BD પરસ્પર O બિંદુમાં OB = OD થાય તે રીતે છેદે છે. જો AB = CD હોય, તો સાબિત કરો કે
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB અથવા ABCD એક સમાંતરબાજુ ચતુષ્કોણ છે.
[સૂચન : D અને Bમાંથી AC પર લંબ દોરો.]
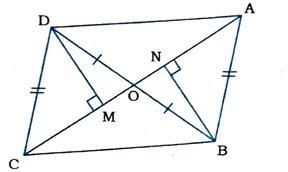
DM ⊥ AC તથા BN ⊥ AC દોરો, જ્યાં M અને N એ AC પરનાં બિંદુઓ છે.
Δ DMO અને Δ BNOમાં,
DO = BO (પક્ષ)
∠DOM = ∠BON (અભિકોણ)
∠DMO = ∠BNO (કાટખૂણા)
∴ ખૂખૂબા મુજબ, Δ DMO ≅ Δ BNO
∴ DM = BN (CPCT)
હવે, Δ DMC અને Δ BNAમાં,
DM = BN
વિકર્ણ DC = વિકર્ણ BA (પક્ષ)
∠DMC = ∠BNA (કાટખૂણા)
∴ કાકબા મુજબ Δ DMC ≅ Δ BNA
∴ ar (DMC) = ar (BNA) ….. (1)
વળી, ar (DMO) = ar (BNO) (Δ DMO ≅ Δ BNO) …… (2)
(1) અને (2)નો સરવાળો લેતાં,
ar (DMC) + ar (DMO) = ar (BNA) + ar (BNO)
∴ ar (DOC) = ar (AOB) (આચ્છાદિત ન થતા હોય તેવા ત્રિકોણો) ….. પરિણામ (i)
હવે, ar (DOC) + ar (COB) = ar (AOB) + ar (COB) (બંને બાજુ ar (COB) ઉમેરતાં)
∴ ar (DCB) = ar (ACB) …. પરિણામ (ii)
Δ DCB અને Δ ACB એક જ પાયા BC પર આવેલા છે અને સમક્ષેત્ર છે.
∴ Δ DCB અને Δ ACB બે સમાંતર રેખાઓની જોડ વચ્ચે આવેલા છે.
∴ DA || CB …. (3)
Δ DMO ≅ Δ BNO પરથી OM = ON મળે.
Δ DMC ≅ Δ BNA પરથી CM = AN મળે.
∴ OM + CM = ON + AN
∴ OC = OA
વળી, OD = OB આપેલ છે.
આમ, ચતુષ્કોણ ABCDના વિકર્ણો AC અને BD પરસ્પર ૦માં દુભાગે છે.
∴ ABCD એક સમાંતરબાજુ ચતુષ્કોણ છે. …… (4)
(3) અને (4) સાથે લેતાં,
DA || CB અથવા ABCD એક સમાંતરબાજુ ચતુષ્કોણ છે. …. પરિણામ (iii)
7. Δ ABCની બાજુઓ AB અને AC પર અનુક્રમે D અને E બિંદુઓ એવી રીતે આવેલાં છે જેથી ar (DBC) = ar (EBC) થાય, તો સાબિત કરો કે DE || BC.
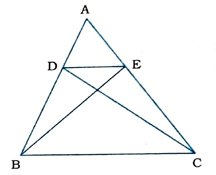
ar (DBC) = ar (EBC)
આથી Δ DBC અને Δ EBC સમક્ષેત્ર છે.
અહીં, Δ DBC અને Δ EBC એક જ પાયા BC પર આવેલ છે અને તેઓ સમક્ષેત્ર છે.
∴ Δ DBC અને Δ EBC બે સમાંતર રેખાઓની જોડ વચ્ચે આવેલા છે.
∴ DE || BC
8. Δ ABCની બાજુ BCને સમાંતર એક રેખા XY છે. જો BE || AC અને CF || AB અને રેખા XY એ BE અને CFને અનુક્રમે E અને F આગળ છેદતી હોય, તો સાબિત કરો કે ar (ABE) = ar (ACF).
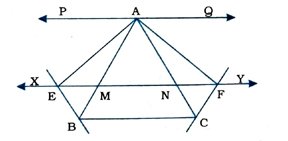
BCને સમાંતર દોરેલ રેખા XY ધારો કે AB અને ACને અનુક્રમે M અને Nમાં છેદે છે.
ચતુષ્કોણ EBCNમાં EN || BC અને BE || CN.
∴ EBCN સમાંતરબાજુ ચતુષ્કોણ છે.
ચતુષ્કોણ MBCFમાં MF || BC અને BM || CF
∴ MBCF સમાંતરબાજુ ચતુષ્કોણ છે.
સમાંતરબાજુ ચતુષ્કોણ EBCN અને MBCF એક જ પાયા BC પર અને સમાંતર રેખાઓની જોડ BC || EF વચ્ચે આવેલા છે.
∴ ar (EBCN) = ar (MBCF)
∴ ar (BME) + ar (MBCN) = ar (MBCN) + ar (CFN)
∴ ar (BME) = ar (CFN) … .. (1)
Δ BME અને Δ CFN એક સમાંતર રેખાની જોડ EF || BCની વચ્ચે આવેલાં છે અને સમક્ષેત્ર છે.
∴ તેમના પાયા સમાન છે.
∴ EM = NF
હવે, Aમાંથી EFને સમાંતર રેખા PQ દોરી શકાય.
તો, Δ AEM અને Δ ANF સમાન પાયા પર અને સમાંતર રેખાની જોડ EF || PQ વચ્ચે આવેલા છે.
∴ ar (AEM) = ar (ANF) …. .. (2)
(1) અને (2)નો સરવાળો લેતાં,
ar (BME) + ar (AEM) = ar (CFN) + ar (ANF)
∴ ar (ABE) = ar (ACF)
9. સમાંતરબાજુ ચતુષ્કોણ ABCDની એક બાજુ ABને બિંદુ P સુધી લંબાવેલી છે. બિંદુ Aમાંથી CPને સમાંતર દોરેલી એક રેખા, CBને Qમાં મળે છે જેથી કરીને સમાંતરબાજુ ચતુષ્કોણ PBQR બને છે. (જુઓ આકૃતિ) તો સાબિત કરો કે
ar (ABCD) = ar (PBQR)
[સૂચન : AC અને PQને જોડો અને ar (ACQ) અને ar (API)ને સરખાવો.]
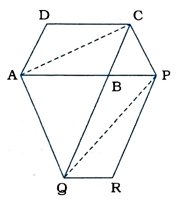
AC અને PQ જોડો.
Δ CAQ અને Δ PAQ એક જ પાયા AQ પર અને એક સમાંતર રેખાની જોડ CP || AQ વચ્ચે આવેલા છે.
∴ ar (CAQ) = ar (PAQ)
∴ ar (ACB) + ar (ABQ) = ar (PBQ) + ar (ABQ) (એકબીજાને આચ્છાદિત ન કરે તેવા ત્રિકોણો)

10. સમલંબ ચતુષ્કોણ ABCDમાં AB || DC છે. વિકર્ણો AC અને BD પરસ્પર એકબીજાને ૦ બિંદુમાં છેદે, તો સાબિત કરો કે
ar (AOD) = ar (BOC).
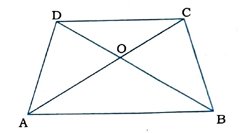
Δ DAB અને Δ CBA એક જ પાયા AB અને સમાંતર રેખાની જોડ AB || CD વચ્ચે આવેલા છે.
∴ ar (DAB) = ar (CBA)
Δ DAB અને Δ CBA બંને એકબીજાને આચ્છાદિત ન કરે તેવા ત્રિકોણો દ્વારા બને છે.
∴ ar (DAB) = ar (AOD) + ar (OAB) અને
ar (CBA) = ar (BOC) + ar (OAB)
∴ ar (AOD) + ar (OAB) = ar (BOC) + ar (OAB)
∴ ar (AOD) = ar (BOC)
11. આપેલ આકૃતિમાં ABCDE પંચકોણ છે. Bમાંથી ACને સમાંતર દોરેલી રેખા DCને Fમાં મળે છે. સાબિત કરો કે,
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
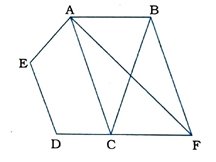
Δ ACB અને Δ ACF એક જ પાયા AC પર અને સમાંતર રેખાની જોડ AC || BF વચ્ચે આવેલા છે.
∴ ar (ACB) = ar (ACF) … પરિણામ (i)
∴ ar (ACF) + ar (AEDC) = ar (ACB) + ar (AEDC) (બંને બાજુ ar (AEDC) ઉમેરતાં)
Δ ACF અને ચતુષ્કોણ AEDC એ એકબીજાને આચ્છાદિત ન ક૨ે તેવી આકૃતિઓ છે અને તેમના યોગ દ્વારા ચતુષ્કોણ AEDF બને છે.
તે જ પ્રમાણે Δ ACB અને ચતુષ્કોણ AEDC એ એકબીજાને આચ્છાદિત ન કરે તેવી આકૃતિઓ છે અને તેમના યોગ દ્વારા પંચકોણ ABCDE બને છે.
∴ ar (AEDF) = ar (ABCDE) …… પરિણામ (ii)
12. એક ગામના એક ખેડૂત પાસે એક ચતુષ્કોણ આકારની જમીનનો ભાગ હતો. આ ગામની ગ્રામપંચાયતે તેની પાસેથી જમીનના એક ખૂણાનો જમીનનો કેટલોક ભાગ સ્વાસ્થ્ય કેન્દ્ર બનાવવા માટે લેવાનો નિર્ણય કર્યો. ખેડૂત આ પ્રસ્તાવ એક શરત સાથે સ્વીકારે છે કે તેને પોતાની જમીનની બાજુમાં તેટલા જ ક્ષેત્રફળની જમીનનો ભાગ મળવો જોઈએ જેથી તેની કુલ જમીનનો આકાર ત્રિકોણ બને, તો તમે દર્શાવો કે આ પ્રસ્તાવ કેવી રીતે શક્ય બનશે.
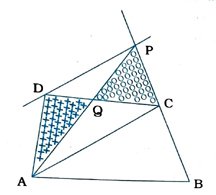
ધારો કે, ચતુષ્કોણ ABCD એ ખેડૂતની ચતુષ્કોણ આકારની જમીન છે.
વિકર્ણ AC દોરો. Dમાંથી વિકર્ણ ACને સમાંતર રેખા દોરો, જે BCને Pમાં છેદે.
PA જોડો, જે CDને Qમાં છેદે.
અહીં, Δ DAC અને Δ PAC એક જ પાયા AC પર અને સમાંતર રેખાની જોડ DP || AC વચ્ચે આવેલા છે.
∴ ar (DAC) = ar (PAC)
∴ ar (DAQ) + ar (QAC) = ar (PQC) + ar (QAC)
∴ ar (DAQ) = ar (PQC)
આમ, બે સમક્ષેત્ર Δ DAQ અને Δ PQC મળે.
આથી ગ્રામપંચાયતે ખેડૂતની જમીન ABCDમાંથી Δ DAQ આકારનો ટુકડો લેવો જોઈએ અને બદલામાં Δ PQC આકારનો ટુકડો ખેડૂતને આપવો જોઈએ, જેથી ખેડૂતની જમીન Δ PAB આકારની બની જાય.
13. સમલંબ ચતુષ્કોણ ABCDમાં AB || DC છે. ACને સમાંતર રેખા, ABને Xમાં અને BCને Yમાં છેદે છે, તો સાબિત કરો કે ar (ADX) = ar (ACY). [સૂચન : CXને જોડો.]

CX જોડો.
Δ ADX અને Δ ACX એક જ પાયા AX ૫૨ અને સમાંતર રેખાઓની જોડ AB || CD વચ્ચે આવેલા છે.
∴ ar (ADX) = ar (ACX) …… (1)
Δ ACX અને Δ ACY એક જ પાયા AC પર અને સમાંતર રેખાઓની જોડ AC || XY વચ્ચે આવેલા છે.
∴ ar (ACX) = ar (ACY) …… (2)
(1) અને (2) પરથી,
ar (ADX) = ar (ACY)
14. આપેલ આકૃતિમાં AP || BQ || CR છે, તો સાબિત કરો કે ar (AQC) = ar (PBR).
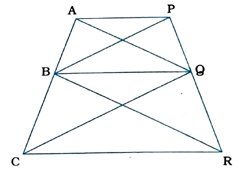
Δ CBQ અને Δ RBQ એક જ પાયા BQ ૫૨ અને સમાંતર રેખાની જોડ BQ || CR વચ્ચે આવેલા છે.
∴ ar (CBQ) = ar (RBQ) …. (1)
Δ ABQ અને Δ PBQ એક જ પાયા BQ પર અને સમાંતર રેખાની જોડ BQ || AP વચ્ચે આવેલા છે.
∴ ar (ABQ) = ar (PBQ) ….. (2)
(1) અને (2)નો સરવાળો લેતાં,
ar (CBQ) + ar (ABQ) = ar (RBQ) + ar (PBQ)
∴ ar (AQC) = ar (PBR) (એકબીજાને આચ્છાદિત ન કરે તેવા ત્રિકોણો)
15. ચતુષ્કોણ ABCDના વિકર્ણો AC અને BD પરસ્પર એકબીજાને O બિંદુએ એવી રીતે છેદે છે કે જેથી ar (AOD) = ar (BOC) થાય, તો સાબિત કરો કે ABCD સમલંબ ચતુષ્કોણ છે.

ar (AOD) = ar (BOC)
∴ ar (AOD) + ar (OAB) = ar (BOC) + ar (OAB) (બંને બાજુ ar (OAB) ઉમેરતાં)
∴ ar (DAB) = ar (CAB)
આમ, Δ DAB અને Δ CAB એક જ પાયા AB પર આવેલા છે અને સમક્ષેત્ર છે.
માટે, પ્રમેય 9.3 મુજબ તેઓ બે સમાંતર રેખાઓની જોડ વચ્ચે આવેલા છે.
આથી DC || AB
ચતુષ્કોણ ABCDમાં DC || AB હોવાથી ચતુષ્કોણ ABCD સમલંબ ચતુષ્કોણ છે.
16. આપેલ આકૃતિમાં ar (DRC) = ar (DPC) છે અને ar (BDP) = ar (ARC) છે, તો ચતુષ્કોણ ABCD અને DCPR સમલંબ ચતુષ્કોણ છે તેમ સાબિત કરો.

ar (DRC) = ar (DPC)
આમ, Δ DRC અને Δ DPC એક જ પાયા DC પર આવેલા છે અને સમક્ષેત્ર છે.
માટે, પ્રમેય 9.3 મુજબ Δ DRC અને Δ DPC બે સમાંતર રેખાઓની જોડ વચ્ચે આવેલા છે.
∴ DC || RP
ચતુષ્કોણ DCPFમાં DC || RP હોવાથી ચતુષ્કોણ DCPR સમલંબ ચતુષ્કોણ છે.
વળી, ar (BDP) = ar (ARC)
∴ ar (DPC) + ar (BDC) = ar (DRC) + ar (ADC) (પરસ્પર આચ્છાદિત ન કરે તેવા ત્રિકોણો)
પરંતુ, ar (DPC) = ar (DRC)
∴ ar (BDC) = ar (ADC)
આમ, Δ BDC અને Δ ADC એક જ પાયા DC પર આવેલા છે અને સમક્ષેત્ર છે.
માટે, પ્રમેય 9.3 મુજબ Δ BDC અને Δ ADC બે સમાંતર રેખાઓની જોડ વચ્ચે આવેલા છે.
∴ AB || DC
આમ, ચતુષ્કોણ ABCDમાં AB || DC હોવાથી ચતુષ્કોણ ABCD સમલંબ ચતુષ્કોણ છે.
હેતુલક્ષી પ્રશ્નોત્તર
1. પ્રત્યેક વિધાન સાચું બને તે રીતે ખાલી જગ્યા પૂરોઃ (ફક્ત અંતિમ જવાબ)
( 1 ) કાટકોણ ત્રિકોણનું ક્ષેત્રફળ = ……..
( 2 ) સમબાજુ ચતુષ્કોણનું ક્ષેત્રફળ = …….
( 3 ) લંબચોરસનું ક્ષેત્રફળ = ……..
( 4 ) સમબાજુ ત્રિકોણનું ક્ષેત્રફળ = ………
( 5 ) ચોરસનું ક્ષેત્રફળ = (………)2/2
2. નીચેના પ્રત્યેક પ્રશ્નનો જવાબ એક સંખ્યા અથવા શબ્દ અથવા વાક્યમાં આપો : (ફક્ત અંતિમ જવાબ)
( 1 ) ABCD સમાંતરબાજુ ચતુષ્કોણ છે. જો Δ CADનું ક્ષેત્રફળ 52 સેમી2 હોય, તો ABCDનું ક્ષેત્રફળ શોધો.
( 2 ) સમાંતરબાજુ ચતુષ્કોણ ABCDનું ક્ષેત્રફળ 144 સેમી2 છે. જો AB = 18 સેમી હોય, તો ABને અનુરૂપ વેધની લંબાઈ શોધો.
( 3 ) એક કાટકોણ ત્રિકોણની બાજુઓના માપ 29 સેમી, 21 સેમી અને 20 સેમી છે, તો તેનું ક્ષેત્રફળ શોધો.
( 4 ) એક ચોરસના વિકર્ણનું માપ 16 સેમી છે, તો તેનું ક્ષેત્રફળ શોધો.
( 5 ) સમબાજુ ચતુષ્કોણ ABCDમાં AC = 12 સેમી અને BD = 18 સેમી હોય, તો ABCDનું ક્ષેત્રફળ શોધો.
3. દરેક પ્રશ્નની નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરીને જવાબ લખો : (ફક્ત અંતિમ જવાબ)
( 1 ) Δ ABC માં AD મધ્યગા છે. જો Δ ABDનું ક્ષેત્રફળ 40 સેમી2 હોય, તો Δ ABCનું ક્ષેત્રફળ …….. સેમી2 હોય.
A. 40
B. 20
C. 80
D. 30
( 2 ) Δ ABC માં AB, BC અને CAના મધ્યબિંદુઓ અનુક્રમે X, Y અને Z છે. જો Δ ABCનું ક્ષેત્રફળ 60 સેમી2 હોય, તો Δ XYZનું ક્ષેત્રફળ …… સેમી2 હોય.
A. 30
B. 15
C. 120
D. 240
( 3 ) Δ ABCમાં AB અને ACનાં મધ્યબિંદુઓ અનુક્રમે X અને Y છે. જો Δ AXYનું ક્ષેત્રફળ 40 સેમી2 હોય, તો Δ ABCનું ક્ષેત્રફળ ….. સેમી2 હોય.
A. 80
B. 160
C. 20
D. 10
( 4 ) સમાંતરબાજુ ચતુષ્કોણ ABCDમાં બાજુ ABનું મધ્યબિંદુ P છે. જો Δ ADPનું ક્ષેત્રફળ 12 સેમી2 હોય, તો ABCDનું ક્ષેત્રફળ …… સેમી2 હોય.
A. 24
B. 6
C. 48
D. 36
( 5 ) સમબાજુ ચતુષ્કોણ ABCDમાં AC = 20 સેમી અને BD = 30 સેમી હોય, તો ABCDનું ક્ષેત્રફળ ……. સેમી2 થાય.
A. 600
B. 300
C. 450
D. 150
4. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે લખો :
( 1 ) ચોરસ ABCDના વિકર્ણ ACની લંબાઈ 20 સેમી2 હોય, તો તેનું ક્ષેત્રફળ 200 સેમી2 થાય.
( 2 ) લંબચોરસ PQRSનું ક્ષેત્રફળ 80 સેમી2 છે. જો PQ = 10 સેમી હોય, તો QR = 16 સેમી હોય.
( 3 ) સમાંતરબાજુ ચતુષ્કોણ PQRSમાં PQ = 12 સેમી અને PQ ને અનુરૂપ વેધ ST = 10 સેમી હોય, તો PQRSનું ક્ષેત્રફળ 60 સેમી2 થાય.
( 4 ) ચોરસ ABCDનું ક્ષેત્રફળ 729 સેમી2 હોય, તો AB = 27 સેમી.
( 5 ) સમબાજુ ચતુષ્કોણ ABCDના વિકર્ણોની લંબાઈ 10 સેમી અને 15 સેમી હોય, તો તેનું ક્ષેત્રફળ 150 સેમી2 થાય.
જવાબો
1. ( 1 ) 1/2 × કાટખૂણો સમાવતી બાજુઓનો ગુણાકાર ( 2 ) 1/2 × વિર્ણોનો ગુણાકાર ( 3 ) લંબાઈ × પહોળાઈ ( 4 ) √3/4 (બાજુ)2 ( 5 ) વિકર્ણ
2. ( 1 ) 104 સેમી2 ( 2 ) 8 સેમી ( 3 ) 210 સેમી2 ( 4 ) 128 સેમી2 ( 5 ) 108 સેમી2
3. ( 1 ) 80 ( 2 ) 15 ( 3 ) 160 ( 4 ) 48 ( 5 ) 300
4. ( 1 ) ખરું ( 2 ) ખોટું ( 3 ) ખોટું ( 4 ) ખરું ( 5 ) ખોટું
સ્વાધ્યાય – 9.4 (વૈકલ્પિક)*
1. સમાંતરબાજુ ચતુષ્કોણ ABCD અને લંબચોરસ ABEF. એ એક જ પાયા પર આવેલા છે અને તેમનાં ક્ષેત્રફળ સમાન છે. સાબિત કરો કે, સમાંતરબાજુ ચતુષ્કોણની પરિમિતિ એ લંબચોરસની પિરિમિત કરતાં વધારે છે.

લંબચોરસ ABEFએ સમાંતરબાજુ ચતુષ્કોણ પણ છે જ. સમાંતરબાજુ ચતુષ્કોણો ABCD અને ABEF એક જ પાયા AB પર છે અને સમક્ષેત્ર છે.
માટે, તેઓ સમાંતરબાજુની જોડ FC || ABની વચ્ચે આવેલા છે. હવે, Δ AFDમાં ∠F એ લંબચોરસ ABEFનો ખૂણો હોવાથી કાટખૂણો છે અને તેથી AD કર્ણ છે.
∴ AD > AF
∴ AD + AB > AF + AB
∴ 2 (AD + AB) > 2 (AF + AB)
∴ સમાંતરબાજુ ચતુષ્કોણ ABCDની પરિમિતિ > લંબચોરસ ABEF ની પરિમિતિ
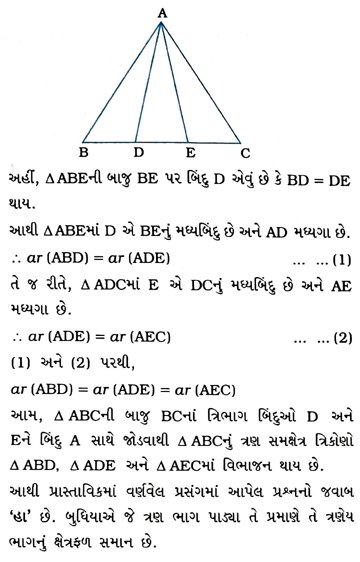
2. આપેલ આકૃતિમાં બાજુ BC પર બે બિંદુઓ D અને E એવી રીતે આવેલાં છે જેથી BD = DE = EC થાય, તો સાબિત કરો કે ar (ABD) = ar (ADE) = ar (AEC) છે.
શું તમે હવે અનુત્તર રહેલા પ્રાસ્તાવિકમાં આપેલ પ્રશ્નનો જવાબ આપી શકશો કે બુધિયાના ખેતરનું બરાબર સમાન ક્ષેત્રફળવાળા ત્રણ ભાગોમાં વિભાજન થયું છે?
[સૂચન : નોંધો કે, BD = DE = EC લેવાથી Δ ABC એ સમાન ક્ષેત્રફળવાળા ત્રણ ત્રિકોણ ABD, ADE અને AECમાં વિભાજિત થાય છે. આ જ રીતે BCને n જેટલા સમાન ભાગમાં વિભાજિત કરતાં બિંદુઓને BCના સામેના શિરોબિંદુ સાથે જોડવાથી તમે Δ ABCનું સમાન ક્ષેત્રફળવાળા n ત્રિકોણોમાં વિભાજન કરી શકો છો.]
3. આપેલ આકૃતિમાં ABCD, DCFE અને ABFE સમાંતરબાજુ ચતુષ્કોણ છે, તો ar (ADE) = ar (BCF) થાય તેમ સાબિત કરો.
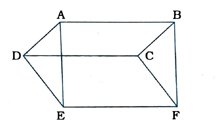
સમાંતરબાજુ ચતુષ્કોણની સામસામેની બાજુઓ સમાન હોય.
સમાંતરબાજુ ચતુષ્કોણ ABCDમાં AD = BC
સમાંતરબાજુ ચતુષ્કોણ DCFEમાં DE = CF
સમાંતરબાજુ ચતુષ્કોણ ABFEમાં AE = BF
હવે, Δ ADE અને Δ BCFમાં,
AD = BC, DE = CF અને AE = BF
∴ બાબાબા મુજબ, Δ ADE ≅ Δ BCF
∴ ar (ADE) = ar (BCF)
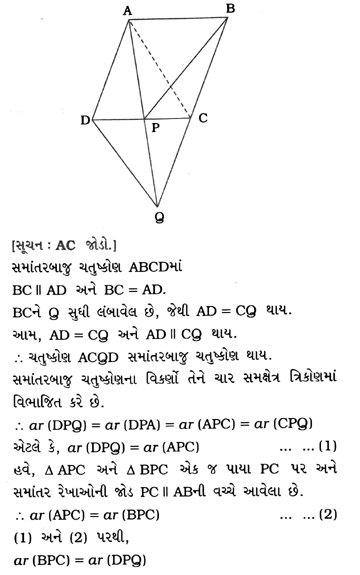
4. આપેલ આકૃતિમાં ABCD એક સમાંતરબાજુ ચતુષ્કોણ છે. BCને બિંદુ Q સુધી એવી રીતે લંબાવો જેથી AD = CQ થાય. જો AQ એ DCને P બિંદુમાં છેદે, તો સાબિત કરો કે ar (BPC) = ar (DPQ).
5. આપેલ આકૃતિમાં ABC અને BDE બે સમભુજ ત્રિકોણ છે. બિંદુ D એ BCનું મધ્યબિંદુ છે. જો AE એ BCને Fમાં છેદે, તો સાબિત કરો કે




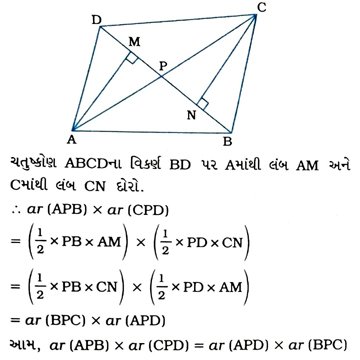
6. ચતુષ્કોણ ABCDના વિકર્ણો AC અને BD પરસ્પર P બિંદુમાં છેદે, તો સાબિત કરો કે
ar (APB) × ar (CPD) = ar (APD) × ar (BPC)
[સૂચન : A અને Cમાંથી BD પર લંબ દોરો.]
7. Δ ABCની બાજુઓ AB અને ACનાં મધ્યબિંદુઓ અનુક્રમે P અને Q છે તથા R એ APનું મધ્યબિંદુ છે, તો સાબિત કરો કે
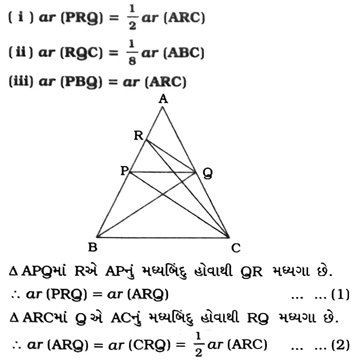
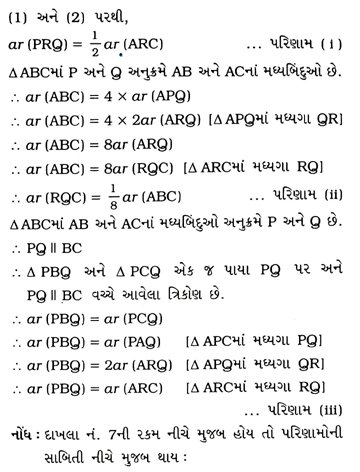
7. Δ ABCની બાજુઓ AB અને BCનાં મધ્યબિંદુઓ અનુક્રમે P અને Q છે તથા R એ APનું મધ્યબિંદુ છે, તો સાબિત કરો કે


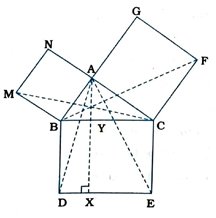
8. આપેલ આકૃતિમાં કાટકોણ ત્રિકોણ ABCમાં ખૂણો A કાટખૂણો છે. BCED, ACFG અને ABMN અનુક્રમે બાજુઓ BC, CA અને AB પર બનેલા ચોરસ છે. રેખાખંડ AX ⊥ DE અને તે બાજુ BCને ૪માં મળે છે, તો સાબિત કરો કે

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here