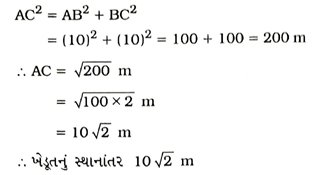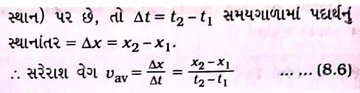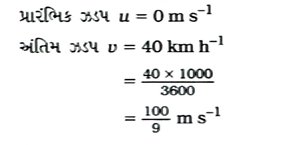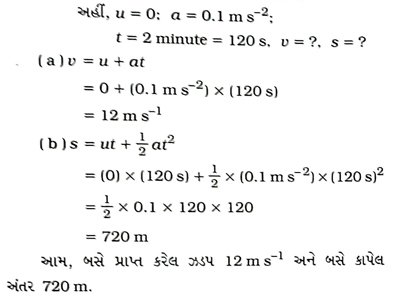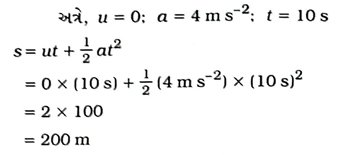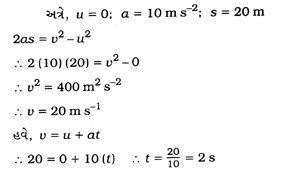Gujarat Board | Class 9Th | Science | Physics | Model Question Paper & Solution | Chapter – 8 Motion (ગતિ)

Gujarat Board | Class 9Th | Science | Physics | Model Question Paper & Solution | Chapter – 8 Motion (ગતિ)

પ્રશ્નોત્તર

પ્રસ્તાવના

પ્રશ્ન 1. ગતિ એટલે શું? એક ઉદાહરણ દ્વારા સ્પષ્ટ કરો કે ગતિ એ સાપેક્ષ ખ્યાલ છે. [2 ગુણ]

ઉત્તર : જ્યારે કોઈ એક પદાર્થ બીજા કોઈ પદાર્થની સાપેક્ષે સમય સાથે પોતાનું સ્થાન બદલે છે, ત્યારે તે પદાર્થ બીજા પદાર્થની સાપેક્ષમાં ગતિ કરે છે તેમ કહેવાય.

→ ધારો કે, એક વિદ્યાર્થી સ્કૂલબસમાં સ્કૂલબૅગ સાથે બેઠો છે અને સ્કૂલબસ તેની શાળા તરફ જઈ રહી છે.

→ આ વિદ્યાર્થી સ્કૂલબૅગને જુએ છે, તો તેને તે સ્થિર લાગે છે અને આ વિદ્યાર્થી બસની બારીમાંથી બહાર તરફ નજ૨ કરે, તો તેને રસ્તા પરનાં ઝાડ, મકાનો, વીજળીના થાંભલા વગે૨ે પોતાનાથી પાછળની તરફ ગતિ કરતાં લાગે છે.

→ આ વખતે વિદ્યાર્થીનો કોઈ મિત્ર રસ્તા ઉપર ઊભો હોય અને તે બસમાંના વિદ્યાર્થીને અને બૅગને જુએ, તો તેને બસમાંનો વિદ્યાર્થી અને બૅગ બંને ગતિ કરતા જણાય છે, જ્યારે રસ્તા પરના ઝાડ, મકાનો વગેરે તેને સ્થિર જણાય છે.

→ આમ, સ્કૂલબૅગ તો તેની તે જ છે પણ ગતિમાન બસમાંથી અવલોકન કરતાં તે સ્થિર જણાય છે અને રસ્તા પરથી અવલોકન કરતાં તે ગતિમાં જણાય છે.

→ આમ, હવે સ્પષ્ટપણે કહી શકાય કે પદાર્થ સ્થિર છે કે ગતિમાં છે તેનો આધાર પદાર્થનું કયા સ્થળેથી અવલોકન કરવામાં આવે છે તેના પર પણ રહેલો છે, જે દર્શાવે છે કે ગતિ એ સાપેક્ષ ખ્યાલ છે.

ઘણી વા૨ ગતિને પરોક્ષ પુરાવાઓની મદદથી અનુમાનિત પણ કરવામાં આવે છે. જેમ કે આપણે પૃથ્વી પર રહીએ છીએ પણ આપણને પૃથ્વીની ગતિનો અહેસાસ થતો નથી; પરંતુ સૂર્યોદય, સૂર્યાસ્ત, ઋતુઓમાં બદલાવ વગેરે તો પૃથ્વીની ગતિને આભારી છે. મોટા ભાગની ગતિઓ જટિલ હોય છે, જેમ કે કેટલાક પદાર્થો સુરેખ પથ પર ગતિ કરતા હોય, કેટલાક વર્તુળમાર્ગે ગતિ કરતા હોય, કેટલાક ચાકગતિ (Rotational motion) કરતા હોય, તો કેટલાક કંપન કે દોલિત ગતિ પણ કરતા હોય છે. તદ્ઉપરાંત કોઈ ગતિ એ બે કે તેથી વધારે પ્રકારની ગતિઓનું સંયોજન પણ હોઈ શકે છે.

8.1 ગતિનું વર્ણન

પ્રશ્ન 2. સંદર્ભબિંદુ એટલે શું? પદાર્થનું સ્થાન દર્શાવવા માટે સંદર્ભબિંદુનો ઉલ્લેખ અનિવાર્ય છે. સમજાવો. [2 ગુણ]

અથવા

સંદર્ભબિંદુ એટલે શું? એક ઉદાહરણ દ્વારા સમજાવો કે પદાર્થનું સ્થાન સાપેક્ષ રાશિ છે.

ઉત્તર : પદાર્થનું સ્થાન દર્શાવવા માટે જે નિયતબિંદુનો સંદર્ભ તરીકે ઉપયોગ કરવામાં આવે છે, તેને સંદર્ભબિંદુ કહે છે.

ઉદાહરણ : એક ગામમાં એક શાળા રેલવે સ્ટેશનથી ઉત્તર દિશા તરફ 2 kmના અંતરે છે અને એસ. ટી. સ્ટૅન્ડથી પશ્ચિમ દિશા તરફ 3 kmના અંતરે છે.

તો પહેલા કિસ્સામાં રેલવે સ્ટેશન સંદર્ભબિંદુ છે, જ્યારે બીજા કિસ્સામાં એસ. ટી. સ્ટૅન્ડ સંદર્ભબિંદુ છે.

→ આમ, સંદર્ભબિંદુ બદલાતાં પદાર્થનું સ્થાન બદલાય છે. તેથી કહી શકાય કે પદાર્થનું સ્થાન દર્શાવવા માટે સંદર્ભબિંદુનો ઉલ્લેખ અનિવાર્ય છે.

બીજા શબ્દોમાં એમ પણ કહી શકાય કે સ્થાન એ નિરપેક્ષ રાશિ નથી પણ સાપેક્ષ રાશિ છે, કારણ કે સંદર્ભબિંદુ બદલાતાં આપેલ પદાર્થનું સ્થાન બદલાય છે.

→ સંદર્ભબિંદુને ઊગમબિંદુ (Origin) પણ કહે છે.

[પદાર્થનું સ્થાન દર્શાવવા માટે (1) સંદર્ભબિંદુ, (2) સંદર્ભબિંદુથી પદાર્થનું અંતર અને (3) સંદર્ભબિંદુથી પાર્થની દિશા જાણવી જરૂરી છે.]

8.1.1 સુરેખ પથ પર ગતિ

પ્રશ્ન 3. અંતર અને સ્થાનાંતરની વ્યાખ્યા આપી, પ્રત્યેકનો SI એકમ જણાવો. [2 ગુણ]

ઉત્તર : અંતર : આપેલા સમયગાળામાં ગતિ કરતા પાર્થે કાપેલ ગતિપથની કુલ લંબાઈને અંતર (અથવા પથલંબાઈ) કહે છે.

→ અંતરનો SI એકમ મીટર (m) છે.

સ્થાનાંતર : પદાર્થના ગતિપથના પ્રારંભિક સ્થાનથી અંતિમ સ્થાન સુધીના લઘુતમ અંતરને સ્થાનાંતર કહે છે.

અથવા

આપેલા સમયગાળામાં ચોક્કસ દિશામાં પાર્થના સ્થાનમાં થતા ફેરફારને સ્થાનાંતર કહે છે.

→ સ્થાનાંતરનો SI એકમ મીટર (m) છે.

[અંતર અને સ્થાનાંતર માટે ‘s’ સંજ્ઞા વપરાય છે. વ્યવહારમાં અંતર અને સ્થાનાંતરના નાના-મોટા એકમો જેવા કે સેન્ટિમીટર (cm), મિલિમીટર (mm), કિલોમીટર (km) પણ ઉપયોગમાં લેવાય છે.]

પ્રશ્ન 4. સ્થાનાંતરનું મૂલ્ય શોધવા માટેનું સૂત્ર મેળવો અને સ્થાનાંતરની દિશા કઈ લેવામાં આવે છે તે જણાવો. [2 ગુણ]

ઉત્તર :

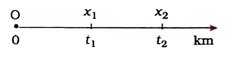
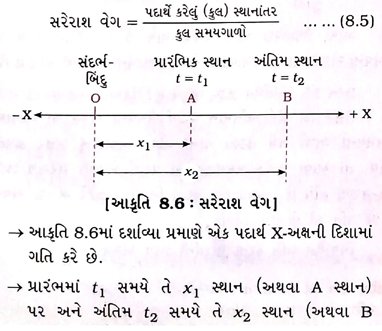
[આકૃતિ 8.1 : t₁ અને t₂ સમયે પદાર્થનું સુરેખ પથ પર સ્થાન] એક નિશ્ચિત સંદર્ભબિંદુ ‘O’ની સાપેક્ષે ધારો કે t₁ સમયે પદાર્થ x₁ સ્થાન પર છે અને t₂ સમયે તે x₂ સ્થાન પર છે, તો t₂ – t₁ સમયગાળામાં પદાર્થનું સ્થાનાંતર (મૂલ્ય) s નીચે મુજબ શોધી શકાય :

s = (અંતિમ સ્થાન) – (પ્રારંભિક સ્થાન)

= x₂ – x₁                                ……. (8.1)

→ સમીકરણ (8.1)ની મદદથી પદાર્થના સ્થાનાંતરનું મૂલ્ય શોધી શકાય છે.

→ સ્થાનાંતરની દિશા પ્રારંભિક સ્થાનથી અંતિમ સ્થાન તરફ હોય છે.

પ્રશ્ન 5. એક ઉદાહરણ દ્વારા અંતર અને સ્થાનાંતર વચ્ચેનો ભેદ સ્પષ્ટ કરો. [2 ગુણ]

ઉત્તર : ગતિનો સાદામાં સાદો પ્રકાર એટલે સુરેખ પથ પર થતી ગતિ.

→ આકૃતિ 8.2માં દર્શાવ્યા મુજબ એક પદાર્થની સુરેખ પથ પર થતી ગતિનો વિચાર કરો.

→ પદાર્થ તેની ગતિની શરૂઆત `O` બિંદુથી કરે છે, જે સંદર્ભબિંદુ છે.

→ C. B . અને A એ પદાર્થના જુદા જુદા સમયે સ્થાન દર્શાવે છે.

→ સૌપ્રથમ પદાર્થ Oથી A ૫૨ અને પછી Aથી C પર સુરેખ પથ પર ગતિ કરીને પહોંચે છે. આ વખતે તે 60 km (0થી 60 km) અને 35 km (60 kmથી 25 km) એટલે કે કુલ OA + AC = 60 km + 35 km = 95 km જેટલું અંતર કાપે છે, જેને પથલંબાઈ પણ કહે છે.

અંતરને દર્શાવવા માટે માત્ર સંખ્યાત્મક મૂલ્ય જ ધ્યાનમાં લેવાય છે, દિશા નહીં. ભૌતિક રાશિના સંખ્યાત્મક મૂલ્યને તેનું માન કહે છે.

→ હવે, પદાર્થના પ્રારંભિક સ્થાન O અને અંતિમ સ્થાન C વચ્ચેના અંતરને (પથલંબાઈને) પાર્થના સ્થાનાંતરનું મૂલ્ય કહે છે, જે અત્રે 25 km છે.

→ આમ, આ ઉદાહરણમાં આપેલ સમયગાળામાં પદાર્થે કાપેલ અંતર 95 km અને સ્થાનાંતર (મૂલ્ય) 25 km છે, જે સમાન નથી.

પ્રશ્ન 6. શું દરેક સંજોગમાં પદાર્થના સ્થાનાંતરનું મૂલ્ય અને તેણે કાપેલ અંતર સમાન હોય છે? યોગ્ય અને જરૂરી ઉદાહરણ આપીને સમજાવો. [4 ગુણ]

અથવા

“પથલંબાઈ (અંતર) હંમેશાં ધન જ હોય છે, જ્યારે સ્થાનાંતર ધન, ઋણ અથવા શૂન્ય હોઈ શકે છે.” આ વિધાન એક યોગ્ય ઉદાહરણ દ્વારા સમજાવો.

ઉત્તર : દરેક સંજોગમાં પદાર્થના સ્થાનાંતરનું મૂલ્ય અને તેણે કાપેલ અંતર સમાન હોતા નથી.

આ હકીકત સમજવા માટે આકૃતિ 8.3માં દર્શાવ્યા મુજબ પદાર્થની ગતિનો વિચાર કરો :

ઉદાહરણ :

કિસ્સો 1 : ધારો કે, પદાર્થ ૦ બિંદુથી ગતિની શરૂઆત કરીને A પર પહોંચે છે, આ ગતિપથ માટે પદાર્થની પથલંબાઈ (અંતર) અને સ્થાનાંતર નીચે મુજબ શોધી શકાય :

પથલંબાઈ = OA

= 60 km

સ્થાનાંતર (અંતિમ સ્થાન A) – (પ્રારંભિક સ્થાન O)

= 60 – 0 = + 60 km

સ્થાનાંતર (મૂલ્ય) = 60 km

આ કિસ્સામાં સ્થાનાંતરનું મૂલ્ય અને પથલંબાઈ સમાન છે તથા સ્થાનાંતરની દિશા ધન X દિશામાં છે.

કિસ્સો 2 : ધારો કે, પદાર્થ O-A-B માર્ગે ગતિ કરીને B પર પહોંચે છે. આ ગતિપથ માટે પદાર્થની પથલંબાઈ (અંતર) અને સ્થાનાંતર નીચે મુજબ શોધી શકાય :

પથલંબાઈ = OA + AB

= 60 km + 25 km

= 85 km

સ્થાનાંતર = (અંતિમ સ્થાન B) – (પ્રારંભિક સ્થાન O)

= 35 – 0

= + 35 km

સ્થાનાંતર (મૂલ્ય) = 35 km

આ કિસ્સામાં સ્થાનાંતરનું મૂલ્ય અને પથલંબાઈ સમાન નથી તથા સ્થાનાંતરની દિશા ધન X દિશામાં છે.

કિસ્સો 3 : ધારો કે, પાર્થ O-A-O માર્ચે ગતિ કરીને O પર પહોંચે છે. આ ગતિપથ માટે પાર્થની પથલંબાઈ (અંતર) અને સ્થાનાંતર નીચે મુજબ શોધી શકાય :

પથલંબાઈ = OA + AO

= 60 km + 60 km

= 120 km

સ્થાનાંતર = (અંતિમ સ્થાન O) – (પ્રારંભિક સ્થાન O)

= 0 – 0

= 0 km

આ કિસ્સામાં સ્થાનાંતરનું મૂલ્ય (0 km) અને પથલંબાઈ (120 km) સમાન નથી.

કિસ્સો 4 : ધારો કે, પદાર્થ પોતાની ગતિની શરૂઆત B બિંદુ આગળથી કરે છે અને B-A-C માર્ગે ગતિ કરીને C પર પહોંચે છે. આ ગતિપથ માટે પાર્થની પથલંબાઈ (અંતર) અને સ્થાનાંતર નીચે મુજબ શોધી શકાય :

પથલંબાઈ = BA + AB + BC

= 25 km + 25 km + 10 km = 60 km

સ્થાનાંતર = (અંતિમ સ્થાન C) – (પ્રારંભિક સ્થાન B)

= 25 – 35 = – 10 km

સ્થાનાંતર (મૂલ્ય) = 10 km

આ કિસ્સામાં સ્થાનાંતરનું મૂલ્ય અને પથલંબાઈ સમાન નથી તથા સ્થાનાંતરની દિશા ઋણ X દિશામાં છે.

ઉપર્યુક્ત ચારેય કિસ્સાઓ પરથી સ્પષ્ટ છે કે –

(1) દરેક સંજોગોમાં પદાર્થના સ્થાનાંતરનું મૂલ્ય અને પદાર્થે કાપેલ અંતર સમાન હોતું નથી.

(2) પથલંબાઈ (અંતર) હંમેશાં ધન જ હોય છે; જ્યારે સ્થાનાંતર (સદિશ રાશિ) ધન, ઋણ અથવા શૂન્ય હોઈ શકે છે.

નોંધ : (1) પાર્થે કાપેલું અંતર તેના ગતિપથની કુલ લંબાઈ દર્શાવે છે, જ્યારે સ્થાનાંતર એ પદાર્થની ગતિની અંતિમ પરિણામી અસર જ દર્શાવે છે.

(2) સ્થાનાંતર પરથી પદાર્થ ક્યા ગતિમાર્ગ પર થઈને સ્થાનાંતર કરે છે તે અંગેની માહિતી મળતી નથી, જ્યારે અંતર પરથી આ અંગેની માહિતી મળી શકે છે.

Intext પ્રશ્નોત્તર

પ્રશ્ન 7. કોઈ પદાર્થ દ્વારા કંઈક અંતર કપાયેલ છે. શું તેનું સ્થાનાંતર શૂન્ય હોઈ શકે? જો હા, તો આપના ઉત્તરને ઉદાહરણ દ્વારા સમજાવો. [2 ગુણ]

ઉત્તર : હા. પદાર્થનું સ્થાનાંતર શૂન્ય હોઈ શકે છે.

ઉપરોક્ત હકીકત ત્યારે જ શક્ય બને છે કે જ્યારે પદાર્થના ગતિપથનું પ્રારંભિક સ્થાન અને અંતિમ સ્થાન એક જ હોય.

ઉદાહરણ : એક વિદ્યાર્થી પોતાના ઘરેથી ચાલીને સ્કૂલે જાય છે અને ત્યાંથી પાછો ફરીને પોતાના ઘરે આવે છે.

તો વિદ્યાર્થીએ કેટલુંક અંતર કાપ્યું હશે પણ તેનું સ્થાનાંતર શૂન્ય હશે.

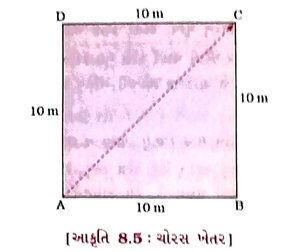
પ્રશ્ન 8. એક ખેડૂત 10 m લંબાઈના એક ચોરસ ખેતરની ધારે ધારે 40 sમાં એક ચક્કર પૂર્ણ કરે છે. 2 મિનિટ 20 સેકન્ડ બાદ આ ખેડૂતે પ્રારંભિક સ્થાનથી કેટલું સ્થાનાંતર કર્યું હશે? [3 ગુણ]

ઉત્તર :

અહીં, ચોરસ ખેતરની સરહદ પર ચાલીને 1 પરિક્રમણના અંતે ખેડૂતે કાપેલું અંતર = ચોરસની પરિમિતિ

= 4 × 10 m

= 40 m

હવે, 1 પરિક્રમણ પૂર્ણ કરવા માટે એટલે કે 40 m તર કાપવા માટે ખેડૂતને લાગતો સમય = 40 S

∴ 2 મિનિટ અને 20 સેકન્ડમાં એટલે કે 140 sમાં ખેડૂત દ્વારા કપાતું અંતર = 140 m

હવે, 40 m = 1 પરિક્રમણ

∴ 140 m = 140/40 પરિક્રમણ = 3.5 પરિક્રમણ

0.5 પરિક્રમણ = 0.5 × 40 m = 20 m

તેથી આકૃતિ 8.5માં દર્શાવ્યા પ્રમાણે ખેડૂતનું પ્રારંભિક સ્થાન A છે. તેથી 2 મિનિટ અને 20 સેકન્ડના અંતે તેનું અંતિમ સ્થાન C હશે.

∴ ખેડૂતનું સ્થાનાંતર = AC

સ્થાનાંતરનું મૂલ્ય શોધવા માટે કાટકોણ A ABC માટે પાયથાગોરસનો પ્રમેય વાપરતાં,

પ્રશ્ન 9. સ્થાનાંતર માટે નીચેના પૈકી કયું સાચું છે? (2 ગુણ)

(a) તે શૂન્ય હોઈ શકે નહિ.

(b) તેનું મૂલ્ય પદાર્થ દ્વારા કપાયેલ અંતર કરતાં વધુ હોય છે.

ઉત્તર :

(a) ખોટું. સ્થાનાંતર શૂન્ય હોઈ શકે છે.

(b) ખોટું. સ્થાનાંતરનું મૂલ્ય કપાયેલ અંતર જેટલું અથવા તેનાથી ઓછું હોય છે.

8.1.9 નિયમિત ગતિ અને અનિયમિત ગતિ

પ્રશ્ન 10. નિયમિત ગતિ અને અનિયમિત ગતિ સમજાવો. [2 ગુણ]

અથવા

યોગ્ય ઉદાહણ વર્ષ નિયમિત અને અનિશ્ચિત ગતિ વય્યેનો તકાવત સ્પષ્ટ કરો.

ઉત્તર : નિયમિત ગતિ કે જો કોઇ વિધાન એમ મ મ રામના એકરારમાં ગાળામાં કરાવવું એ શાખા) અંતર કાપતા હોય, તો તે પદાથ માં ગતિ કરે છે. તેમ કહેવાય.

ઉદાહરણ ધારો કે એક પાત્ર છે! આવ. પહેલી બેમાં, બીજું 5 ) તરીજી સેકન્ડમાં, 5) 1 શ્રીજી એન્ડમાં અને 5.) વર શોધી એન્ડમાં કાપે છે.

અહીં, પદાર્થ સમયના એકસરખા ગાળામાં એકસરનું યંત્ર ખ પથ પર કાપે છે. તેથી આ પદાર્થ નિમિત ગતિ કરે છે તેમ કહેવાય,

અનિયમિત ગતિ જો કોઈ ગતિમાન પદાર્થ સુખ પથ પર સમયના એકરારખા ગાળામાં એકસરખું અંતર (એક શાખા) કાપો. ન હોય, તો તે પદાર્થ અનિયમિત ગતિ કરે છે. તેમ કહેવાય.

ઉદાહરણ : ( 1 ) ભરચક રસ્તા પર થતી કાર ની ગતિ,

રસ્તા પર ટ્રાફિક હશે, તો કારની ઝપ ધીમી પડશે. તો ખુલ્લો હશે, તો કાર ઝડપથી આગળ વધશે અને ટ્રાફિક સિગ્નલ લાલ થતાં તે ત્યાં થોભી જશે,

આમ, કાર સમયના એકસરખા ગાળામાં એક્સરખું અંતર કાપતી નથી. તેથી તે નિયમિત ગતિ કરે છે. તેમ કહેવાય.

( 2 ) એક ગાર્ડનમાં કોઈ માણસનાં દોડવાની ગતિ.

8.2 ગતિના દરનું માપન

પ્રશ્ન 11. ઝડપ નામની ભૌતિક રાશિ શા માટે વ્યાખ્યાયિત કરવામાં આવે છે? ઝડપની વ્યાખ્યા લખો. [2 ગુણ]

ઉત્તર : ઘણી વાર જુદા જુદા પદાર્થો એકસરખું અંતર કાપવા માટે જુદો જુદો સમય લેતાં હોય છે. તેમાંના કેટલાંક ઝડપથી અને કેટલાંક ધીરેથી ગતિ કરતા હોય છે. ગતિનો દર એટલે કે ગતિની ત્વરા જુદા જુદા પદાર્થોની જુદી જુદી હોય છે અને કેટલીક વખત જુદા જુદા પદાર્થોની ગતિની ત્વરા સમાન હોય છે.

ગતિનો દર માપવાની પદ્ધતિઓમાંથી એક પદ્ધતિ મુજબ પદાર્થનો ગતિનો દર, તે પદાર્થ 1 સેકન્ડમાં કેટલું અંતર કાપે છે તે શોધીને નક્કી કરવામાં આવે છે. આ ભૌતિક રાશિને ઝડપ કહે છે.

વ્યાખ્યા : ગતિમાન પદાર્થ એકમ સમયમાં કાપેલા અંતરને તે પદાર્થની ઝડપ કહે છે.

પ્રશ્ન 12. ઝડપનું માત્ર સૂત્ર લખો અને તેનો SI એકમ જણાવો. તે † સદિશ રાશિ છે કે †† અદિશ? [2 ગુણ]

ઉત્તર :

પ્રશ્ન 13. સરેરાશ ઝડપ નામની ભૌતિક રાશિ શા માટે વ્યાખ્યાયિત કરવામાં આવે છે? એક ઉદાહરણ આપો. [2 ગુણ]

ઉત્તર : વ્યવહારમાં મોટા ભાગના ગતિમાન વાહનો અનિયમિત ગતિ કરતાં હોઈ જુદા જુદા સમયે વાહનોની ઝડપમાં વધ-ઘટ થતી હોય છે. આવા સંજોગોમાં વાહનની ગતિનો દર જાણવા માટે ‘સરેરાશ ઝડપ’ નામની ભૌતિક રાશિ વ્યાખ્યાયિત કરવામાં આવે છે.

ઉદાહરણ : એક મોટરકાર અમદાવાદથી સવારે 8 વાગે ઉપડીને તે જ દિવસે 10 વાગે વડોદરા પહોંચે છે. અમદાવાદ અને વડોદરા વચ્ચેનું અંતર 100 km છે.

આમ, કહી શકાય કે આ મોટરકારે 100 km અંતર 2 કલાકમાં કાપ્યું છે. હવે, મોટરકારમાંના સ્પીડોમિટર વડે જુદા જુદા સમયે તેની ઝડપ જુદી જુદી માલૂમ પડે છે. આવી પરિસ્થિતિમાં મોટરકારની ઝડપ જાણવાનો કોઈ મતલબ રહેતો નથી, કારણ કે તે સમયે સમયે બદલાયા કરે છે. તેથી સરેરાશ ઝડપ નામની ભૌતિક રાશિ વ્યાખ્યાયિત કરવામાં આવે છે.

પ્રશ્ન 14, સરેરાશ ઝડપ એટલે શું? તેનું સૂત્ર લો અને એક યોગ્ય ઉદાહરણ વડે સમજાવો કે સરેરાશ ઝડપ એ જુદી જુદી ઝોની સરેરાશ નથી પણ હકીકતમાં સમયના એકસરખા સમયગાળામાં મેળવેલ ઝડપનાં મૂલ્યોની સરેરાશ છે. [3 ગુણ)

ઉત્તર : સરેરાશ ઝડપ : પદાર્થે કાપેલું કુલ અંતર અને તે અંતર કાપવા માટે લાગતા કુલ સમયના ગુન્નોત્તરને તે પાર્થની સંશ ઝડપ કર્યું છે.

આમ, ઉદાહરણ પરથી સ્પષ્ટ થાય છે કે સરેરાશ ઝડપ એ સમયના એકસરખા સમયગાળામાં મેળવેલ ઝડપનાં મૂલ્યોની સરેરાશ છે.

પ્રશ્ન 15. નિયમિત ઝડપ એટલે શું? ટૂંકમાં સમજાવો. [2 ગુણ]

ઉત્તર : જો કોઈ ગતિમાન પદાર્થ સમયના એકસરખા ગાળામાં (સમયનો ગાળો ગમે તેટલો નાનો હોય) એકસરખું અંતર કાપતો હોય, તો આવા પ્રત્યેક સમયગાળામાં પાર્થે મેળવેલ સરેરાશ ઝડપ એકસરખી હોય છે. આથી આ પદાર્થ નિયમિત ઝડપે અથવા અચળ ઝડપે ગતિ કરે છે તેમ કહેવાય.

નિયમિત ગતિ કરતા પદાર્થની ઝડપ અચળ હોય છે.

8.2.1 દિશા સાથે ઝડપ

પ્રશ્ન 16. વેગ નામની ભૌતિક રાશિ શા માટે વ્યાખ્યાયિત કરવામાં આવે છે? વેગની વ્યાખ્યા લખો. [2 ગુણ]

ઉત્તર : પદાર્થની ઝડપ શોધતી વખતે ગતિમાન પદાર્થની ગતિની દિશા ધ્યાનમાં લેવામાં આવતી નથી, કારણ કે ઝડપ અદિશ રાશિ છે.

પરંતુ જો પદાર્થની ઝડપ સાથે તેની ગતિની દિશાને સાંકળવામાં આવે તો પદાર્થની ગતિની ત્વરા એટલે કે ગતિનો દર વિશાળ અને વ્યાપક બની જાય છે અર્થાત્ ગતિમાન પદાર્થ પ્રારંભિક સ્થાનથી કઈ દિશામાં અને કેટલા દરથી અંતિમ સ્થાને પહોંચે છે તે જાણી શકાય છે.

જે રાશિ ગતિનો દર અને દિશા બંનેને એકસાથે વર્ણવે છે, તેને વેગ કહે છે.

વ્યાખ્યા : ગતિમાન પદાર્થે એકમ સમયમાં કરેલા સ્થાનાંતરને પદાર્થનો વેગ કહે છે.

અથવા

ગતિમાન પદાર્થના સ્થાનાંતરના (અથવા સ્થાનમાં થતા ફેરફારના) સમયદરને પદાર્થનો વેગ કહે છે.

પ્રશ્ન 17. વેગનું માત્ર સૂત્ર લખો અને તેનો SI એકમ જણાવો. તે સદિશ રાશિ છે કે અદિશ? [2 ગુણ]

ઉત્તર :

પ્રશ્ન 18. સરેરાશ વેગની વ્યાખ્યા આપી તેની સમજૂતી આપો. [3 ગુણ]

ઉત્તર : ગતિમાન પદાર્થે કરેલું કુલ સ્થાનાંતર અને તે માટે લાગતા કુલ સમયગાળાના ગુણોત્તરને પદાર્થનો સરેરાશ વેગ કહે છે.

→ સરેરાશ વેગનું મૂલ્ય અને દિશા ફક્ત સ્થાનાંતર પર આધાર રાખે છે. પદાર્થ તેના પ્રારંભિક સ્થાનથી શરૂ કરી ક્યા માર્ગે થઈને કેટલા વળાંકો લઈને અંતિમ સ્થાન પર પહોંચે છે તે ધ્યાનમાં લેવાતું નથી.

દા. ત., એક વિદ્યાર્થી સાઇક્લ લઈને ઘરેથી 15 km/hની સરેરાશ ઝડપે ગતિ કરીને થોડાક સમય પછી પાછો ફરીને પોતાના ઘરે આવે છે, તો અહીં વિદ્યાર્થીનું પ્રારંભિક સ્થાન અને અંતિમ સ્થાન એક જ હોવાથી તે વિદ્યાર્થીનું સ્થાનાંતર શૂન્ય થશે. તેથી વિદ્યાર્થીના સરેરાશ વેગનું મૂલ્ય પણ શૂન્ય થશે.

પ્રશ્ન 19. પદાર્થની ગતિના દરનું મૂલ્ય કેવા સંજોગોમાં સરેરાશ વેગના મૂલ્યના પદમાં શોધવામાં આવે છે? સરેરાશ વેગ ક્યારે પદાર્થના પ્રારંભિક અને અંતિમ વેગના અંકગણિતીય સરેરાશ જેટલો લેવામાં આવે છે? [2 ગુણ]

ઉત્તર : પદાર્થનો વેગ અચળ અથવા ચલિત હોઈ શકે છે. વેગ ત્રણ રીતે બદલાઈ શકે છે ઃ વેગનું મૂલ્ય (ઝડપ) બદલાવાથી, ગતિની દિશા બદલાવાથી, ગતિની દિશા અને ઝડપ બંને બદલાવાથી.

→ જ્યારે પદાર્થ સુરેખ પથ પર બદલાતાં વેગથી ગતિ કરતો હોય ત્યારે તેની ગતિના દરનું મૂલ્ય, સરેરાશ વેગના મૂલ્યના પદમાં દર્શાવવામાં આવે છે.

→ જ્યારે પદાર્થનો વેગ નિયમિત રીતે બદલાતો હોય (વધતો હોય અથવા ઘટતો હોય) ત્યારે તેના સરેરાશ વેગને તેના પ્રારંભિક વેગ અને અંતિમ વેગના અંકગણિતીય સરેરાશ જેટલો લેવામાં આવે છે.

પ્રશ્ન 20. નિયમિત વેગ એટલે શું? અચળ વેગી ગતિ માટેની જરૂરી શરતો જણાવો. [3 ગુણ]

ઉત્તર : જો કોઈ ગતિમાન પદાર્થનો વેગ સમયની સાથે અચળ જળવાઈ રહેતો હોય, તો તે પદાર્થ નિયમિત વેગથી અથવા અચળ વેગથી ગતિ કરે છે તેમ કહેવાય.

જ્યારે કોઈ ગતિમાન પદાર્થ એક ચોક્કસ દિશામાં અચળ ઝડપથી ગતિ કરતો હોય, તો તે પદાર્થનો વેગ અચળ જળવાઈ રહે છે.

અચળ વેગી ગતિ માટે નીચેની બે શરતો પળાવી જોઈએ : (1) પદાર્થ અચળ ઝડપે ગતિ કરતો હોવો જોઈએ. (2) પદાર્થના વેગની દિશા બદલાવી જોઈએ નહીં.

[જો ગતિમાન પદાર્થના વેગનું મૂલ્ય (એટલે કે ઝડપ) અથવા ગતિની દિશા અથવા બંને બદલાતાં હોય તો તેનો વેગ બદલાય છે તેમ કહેવાય.]

Intext પ્રશ્નોત્તર

પ્રશ્ન 21. ઝડપ અને વેગ વચ્ચેનો ભેદ સ્પષ્ટ કરો. [2 ગુજ઼]

ઉત્તર :

પ્રશ્ન 22. કઈ પરિસ્થિતિમાં પદાર્થના સરેરાશ વેગ અને સરેરાશ ઝડપનાં મૂલ્યો સમાન થાય? [1 ગુણ]

ઉત્તર : જ્યારે પદાર્થ સુરેખ પથ પર એક જ દિશામાં ગતિ કરે છે ત્યારે તેના સરેરાશ વેગ અને સરેરાશ ઝડપનાં મૂલ્યો સમાન થાય.

પ્રશ્ન 23. વાહનનું ઓડોમિટર શું માપે છે? [1 ગુણ્ણ]

ઉત્તર : વાહનનું ઓડોમિટર વાહને કાપેલું અંતર માપે છે.

પ્રશ્ન 24. જ્યારે કોઈ પદાર્થ નિયમિત ગતિ કરતો હોય ત્યારે તેનો ગતિપથ કેવો દેખાશે? [1 ગુણ]

ઉત્તર : પદાર્થનો ગતિપથ સુરેખ હશે.

પ્રશ્ન 25. એક પ્રયોગ દરમિયાન અવકાશયાનમાંથી એક સિગ્નલને પૃથ્વી પરના સ્ટેશન સુધી પહોંચતાં 5min જેટલો સમય લાગે છે. પૃથ્વી પરના સ્ટેશનથી અવકાશયાનનું અંતર કેટલું હશે? સિગ્નલનો રંગ પ્રકાશના વેગ જેટલો જ એટલે કે 3 × 10⁸ ms^-1 છે. [2 ગુજ઼]

ઉકેલ : સમય t = 5 minute = 5 × 60 s = 300 s

8.3 વેગના ફેરફારનો દર

પ્રશ્ન 26, પ્રવેગ નામની ભૌતિક રાશિ શા માટે વ્યાખ્યાયિત કરવામાં આવે છે? પ્રવેગની વ્યાખ્યા લખો. [2 ગુણ]

ઉત્તર : સુરેખ પથ પર પદાર્થની નિયમિત ગતિ દરમિયાન પદાર્થનો વેગ સમય સાથે અચળ જળવાઈ રહે છે. આ પરિસ્થિતિમાં સમયના કોઈ પણ ગાળા દરમિયાન પદાર્થના વેગમાં થતો ફે૨ફા૨ શૂન્ય હોય છે.

પણ પદાર્થની અનિયમિત ગતિ દરમિયાન તેનો વેગ સમય સાથે બદલાય છે. જુદા જુદા ક્ષણે અને ગતિપથના જુદાં જુદાં બિંદુઓએ વેગનાં મૂલ્યો જુદાં જુદાં હોય છે. તેથી આવી પરિસ્થિતિમાં સમયના કોઈ પણ ગાળા દરમિયાન પદાર્થના વેગમાં થતો ફેરફાર શૂન્ય હોતો નથી.

ગતિમાન પદાર્થના વેગમાં સમય સાથે થતા ફેરફારોનો અભ્યાસ કરવા માટે ‘પ્રવેગ’ નામની ભૌતિક રાશિ વ્યાખ્યાયિત કરવામાં આવે છે.

વ્યાખ્યા : એકમ સમયમાં ગતિમાન પદાર્થના વેગમાં થતા ફેરફારને પ્રવેગ કહે છે.

અથવા

ગતિમાન પદાર્થના વેગમાં થતા ફેરફારના સમયદરને પ્રવેગ કહે છે.

પ્રશ્ન 27. પ્રવેગનું માત્ર સૂત્ર લખો અને તે પરથી પ્રવેગી ગતિ અને પ્રતિપ્રવેગી ગતિ સમજાવો. પ્રવેગનો એકમ જણાવો. તે દિશ રાશિ છે કે અદિશ તે જણાવો. [3 ગુણ]

ઉત્તર : પ્રવેગ એટલે એકમ સમયમાં વેગમાં થતા ફેરફારનું માપ.

→ પ્રવેગ સદિશ રાશિ છે અને વ્યાપકરૂપે પ્રવેગની દિશા વેગના ફેરફારની દિશામાં હોય છે.

પ્રશ્ન 28. પ્રવેગ અને પ્રતિપ્રવેગનાં બે-બે ઉદાહરણો આપો.

ઉત્તર : પ્રવેગનાં ઉદાહરણો : ( 1 ) કોઈ વાહનને પ્રવેગક (Accelerator = ઍક્સેલરેટર) આપવામાં આવે, તો તેના વેગમાં વધારો થાય છે અને તે પ્રવેગી ગતિ કરે છે.

( 2 ) અમુક ઊંચાઈએથી મુક્ત પતન કરતા દડાના વેગમાં સતત વધારો થાય છે, એટલે કે દડો પ્રવેગી ગતિ કરે છે.

પ્રતિપ્રવેગનાં ઉદાહરણો : ( 1 ) ઊર્ધ્વદિશામાં ઉછાળવામાં આવેલા દડાનો વેગ સતત ઘટે છે, એટલે કે દડો પ્રતિપ્રવેગી ગતિ કરે છે.

( 2 ) ગતિ કરતા વાહનને બ્રેક લગાડવામાં આવે ત્યારે તે વાહન પ્રતિપ્રવેગી ગતિ કરે છે.

પ્રશ્ન 29. નિયમિત પ્રવેગી અને નિયમિત પ્રતિપ્રવેગી ગતિ એટલે શું? તેના એક-એક ઉદાહરણ આપો. [2 ગુણ]

ઉત્તર : નિયમિત પ્રવેગી ગતિઃ સુરેખ ૫થ ૫૨ એક જ દિશામાં ગતિ કરતા પદાર્થના વેગમાં થતો વધારો સમયના એકસરખા ગાળામાં સમાન રહેતો હોય, તો તે પદાર્થ નિયમિત પ્રવેગી ગતિ કરે છે એમ કહેવાય.

ઉદાહરણ : મુક્ત પતન કરતા પદાર્થની ગતિ.

નિયમિત પ્રતિપ્રવેગી ગતિઃ સુરેખ પથ પર એક જ દિશામાં ગતિ કરતા પદાર્થના વેગમાં થતો ઘટાડો સમયના એકસરખા ગાળામાં સમાન રહેતો હોય, તો તે પદાર્થ નિયમિત પ્રતિપ્રવેગી ગતિ કરે છે એમ કહેવાય.

ઉદાહરણ : ઊર્ધ્વદિશામાં ફેંકવામાં આવેલા પદાર્થની ગતિ.

પ્રશ્ન 30, નિયમિત પ્રવેગી ગતિ યોગ્ય ઉદાહરણ આપીને સમજાવો. [3 ગુણ)

ઉત્તર : સુરેખ પથ પર એક જ દિશામાં ગતિ કરતા પદાર્થના વેગમાં થતો વધારો સમયના એકસરખા ગાળામાં સમાન રહેતો હોય, તો તે પદાર્થ નિયમિત પ્રવેગી ગતિ કરે છે એમ કહેવાય.

ઉદાહરણ : મુક્ત પતન કરતા પદાર્થની ગતિ.

મુક્ત પતન : જ્યારે કોઈ પદાર્થને અમુક ઊંચાઈએથી મુક્ત કરવામાં આવે છે ત્યારે તેનો પ્રારંભિક વેગ (u) શૂન્ય હોય છે. તેના પર લાગતું ઘર્ષણબળ નજીવું હોવાથી તેને અવગણતાં, તેના પ્રવેગનું મૂલ્ય (ગુરુત્વપ્રવેગ g જેટલું) 9.8 m s^-2 હોય છે તથા તેનો ગતિપથ સુરેખ હોય છે.

આ પ્રકારની ગતિને મુક્ત પતન કહે છે.

દા. ત., ટાવરની ટોચ પરથી મુક્ત પતન કરતો દડો એ નિયમિત પ્રવેગી ગતિનું ઉદાહરણ છે.

→ આકૃતિ 8.7માં ટાવરની ટોચ પરથી મુક્ત પતન કરતા દડા માટે પ્રત્યેક સેકન્ડે દડાનું સ્થાન, તેનો વેગ અને જે-તે સમયે તેનો પ્રવેગ દર્શાવેલ છે.

→ આકૃતિ પરથી સ્પષ્ટ છે કે પ્રત્યેક 1 સેકન્ડના સમયગાળામાં દડાના વેગમાં થતો વધારો એકસરખો રહેતો હોવાથી અને તેની ગતિની દિશા બદલાતી ન હોવાથી દડો નિયમિત અથવા અચળ પ્રવેગી ગતિ કરે છે તેમ કહેવાય.

→ દડાનો પ્રવેગ 9.8 m s^-2 છે એટલે કે દડાના વેગમાં દર સેકન્ડે 9.8 ms^-1 જેટલો એકસરખો વધારો થાય છે.

પ્રશ્ન 31. અનિયમિત પ્રવેગી ગતિ એટલે શું? તેનું એક ઉદાહરણ આપો. [2 ગુણ]

ઉત્તર : કોઈ પદાર્થના વેગનો બદલાવવાનો (ફેરફારનો) દર અનિયમિત હોય, તો તે પદાર્થ અનિયમિત પ્રવેગી ગતિ કરે છે તેમ કહેવાય.

ઉદાહરણ : ટ્રાફિકવાળા રસ્તા પર વાહનની ગતિ.

→ ટ્રાફિકવાળા રસ્તા પર વાહનનો પ્રવેગ વારંવાર બદલાતો હોય છે. આથી વાહનની ગતિ અનિયમિત પ્રવેગી ગતિ કહેવાય છે.

Intext પ્રશ્નોત્તર

પ્રશ્ન 32. તમે કોઈ વસ્તુની બાબતમાં ક્યારે કહી શકો કે,

(i) તે અચળ પ્રવેગથી ગતિ કરે છે?

(ii) તે અસમાન પ્રવેગથી ગતિ કરે છે? [2 ગુણ]

ઉત્તર : ( i ) જ્યારે પદાર્થ સુરેખ પથ પર ગતિ કરતો હોય અને એકસરખા સમયગાળામાં તેનો વેગ એકસરખા પ્રમાણમાં વધતો હોય, તો પદાર્થ અચળ પ્રવેગી કે નિયમિત પ્રવેગી ગતિ કરે છે તેમ કહેવાય.

(ii) જ્યારે પદાર્થનો વેગ એકસરખા સમયગાળામાં જુદા જુદા પ્રમાણમાં બદલાતો હોય, તો પદાર્થનો પ્રવેગ અનિયમિત છે તેમ કહેવાય.

પ્રશ્ન 33. એક બસની ગતિ 5sમાં 80kmh-1થી ઘટીને 60 km h⁻¹ થઈ જાય છે. બસનો પ્રવેગ શોધો. [2 ગુણ]

ઉકેલ :

પ્રશ્ન 34. એક ટ્રેન રેલવે સ્ટેશનથી ગતિનો પ્રારંભ કરે છે અને અચળ પ્રવેગથી ગતિ કરી 10minમાં 40 km h^-1 ની ઝડપ પ્રાપ્ત કરે છે, તો તેનો પ્રવેગ શોધો. [2 ગુણ]

ઉકેલ :

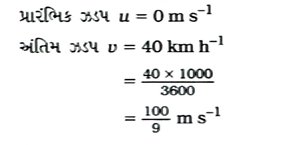
8.4 ગતિનું આલેખીય નિરૂપણ

પ્રશ્ન 35. આલેખનું મહત્ત્વ સમજાવો. [2 ગુણ]

ઉત્તર : ઘણી બધી જુદી જુદી ઘટનાઓ | બનાવોને લગતી મુળભુત માહિતી આલેખો વડે સરળતાથી મેળવી શકાય છે.

દા. ત., ( 1 ) એકદિવસીય ક્રિકેટ-મૅચના પ્રસારણ દરમિયાન ઊભા સ્તંભઆલેખ (ઊર્ધ્વબાર ગ્રાફ) વડે ટીમનો રન-રેટ (રનનો દર) દરેક ઓવરમાં કેટલો છે તે જાણી શકાય છે.

( 2 ) બે ચલ (ધારો કે x અને પુ) ધરાવતા સુરૈખીય સમીકરણનો ઉકેલ મેળવવા માટે સુરેખ આલેખ મદદરૂપ થાય છે.

→ પદાર્થની ગતિનું વર્ણન કરવા માટે સુરેખ આલેખનો ઉપયોગ થાય છે. આ કિસ્સામાં સુરેખ આલેખ એક ભૌતિક રાશિ (જેમ કે અંતર અથવા વેગ), બીજી ભૌતિક રાશિ (જેમ કે સમય) પર આધારિત છે તેમ દર્શાવે છે.

પ્રશ્ન 36. આલેખ કેવી રીતે દોરવામાં આવે છે? સમજાવો.

ઉત્તર :

આલેખ દોરતી વખતે નીચેના મુદ્દાઓ ક્રમિક ધ્યાનમાં લેવામાં આવે છે :

( 1 ) આકૃતિ 8.8માં દર્શાવ્યા મુજબ, સૌપ્રથમ આલેખપેપર ઉપ૨ એકબીજાને લંબ એવી બે રેખાઓ OX અને OY દોરો, રેખા Oxને X-અક્ષ અને OYને Y-અક્ષ કહે છે.

બંને અક્ષના છેદબિંદુ ‘O’ને ઊગમબિંદુ કહે છે. તેના યામ (0,0) છે.

( 2 ) X-અક્ષ પર સ્વતંત્ર ચલ રાશિ અને Y-અક્ષ પર પરતંત્ર ચલ રાશિ દર્શાવો.

દા. ત., વેગ− સમય(વંચાય : વેગ વિરુદ્ધ સમય)ના આલેખમાં વેગ પરતંત્ર ચલ રાશિ છે, જે Y-અક્ષ પર લેવામાં આવે છે અને સમય સ્વતંત્ર ચલ રાશિ છે, જે X-અક્ષ ૫૨ લેવામાં આવે છે.

વિંગ પરતંત્ર ચલ ચિત્ર કહેવાય છે અને સમય સ્વતંત્ર ચલ ચિશ કહેવાય છે, કારણ કે વૈગ સમય પર આધારિત હોય છે, સમય વેગ પર આધારિત નથી,1

( 3 )X અને Y અક્ષ પર યોગ્ય પ્રમાણમાપ સાથે આ બને શિઓના મૂલ્યો દર્શાવો.

સાચા સામાન્ય રીતે ઊગમબિંદુ પર બંને અક્ષ પરની શિશઓના મુલ્ય શૂન્ય લેવામાં આવે છે,

( 4 ) સ્વતંત્ર ચલ રાશિ xને અનુરૂપ પરતંત્ર ચલ રશિના મૂલ્ય પ્રુથી રચાતી પ્રત્યેક ક્રમયુક્ત જોડ (x, y)ને આલેખપેપર પર બિંદુઓ વડે દર્શાવો.

( 5 ) આ બધા બિંદુઓને જોડતો Smooth વક્ર અથવા સુરેખા દોરો.

આ રીતે મળતા આલેખનું સ્વરૂપ માહિતીના પ્રકાર મુજબ સુરેખ અથવા વક્રાકાર હોય છે,

8.4.1 અંતર – સમયના આલેખો 

પ્રશ્ન 37. અચળ ઝડપથી ગતિ કરતા પદાર્થ માટે અંતર – સમયનો આલેખ દોરો અને તેના પરથી પદાર્થની ઝડપ કેવી રીતે શોધી શકાય છે તે સમજાવો. [3 ગુણ]

ઉત્તર :

→ જ્યારે પદાર્થ સુરેખ પથ પર એકસરખા સમયગાળામાં એકસરખું અંતર કાપે છે ત્યારે તે અચળ | નિયમિત ઝડપે ગતિ કરે છે તેમ કહેવાય છે.

આ હકીકત દર્શાવે છે કે પદાર્થે કાપેલું અંતર, પદાર્થે તે અંતર કાપવા માટે લીધેલા સમયના સમપ્રમાણમાં હશે. તેથી અચળ ઝડપથી ગતિ કરતા પદાર્થનો અંતર વિરુદ્ધ સમયનો આલેખ સુરેખા હોય છે.

→ આલેખનો OB ભાગ દર્શાવે છે કે અંતર, સમય સાથે એકસરખા દરે વધે છે.

અંતર – સમયના આલેખ પરથી પદાર્થની ઝડપ નીચે મુજબ શોધી શકાય છે :

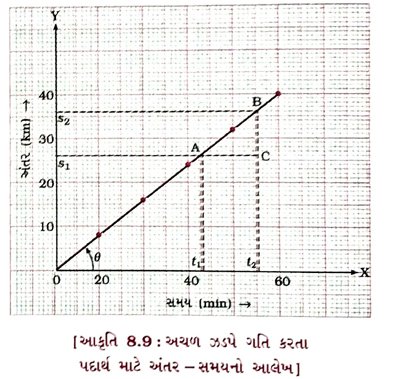
→ આકૃતિ 8.9માં દર્શાવ્યા મુજબ આલેખનો નાનો વિભાગ AB વિચારો.

→ A બિંદુ આગળથી X-અક્ષને સમાંતર એક રેખા અને B બિંદુ આગળથી Y-અક્ષને સમાંતર એક રેખા દોરો.

→ આ બંને રેખાઓ એકબીજીને C બિંદુ આગળ મળે છે અને કાટકોણ Δ ABC રચે છે.

→ હવે, આલેખ ઉપર AC એ સમયનો તફાવત (t₂ − t₁) અને BC એ અંતરનો તફાવત (s₂ − s₁) દર્શાવે છે.

→ આલેખ ઉપરથી સ્પષ્ટ છે કે જ્યારે પદાર્થ Aથી B પર પહોંચે છે ત્યારે તે (s₂ − s₁) જેટલું અંતર (t₂ − t₁) સમયગાળામાં કાપે છે.

∴ આલેખ પરથી પદાર્થની ઝડપ નીચે મુજબ શોધી શકાય :

→ રેખા OBનો ઢાળ m = tan θ છે; જ્યાં, θ = રેખા OB એ ધન X દિશા સાથે વિષમઘડી દિશામાં આંતરેલો ખૂણો.

→ સુરેખ આલેખ માટે ઢાળનું મૂલ્ય હંમેશાં અચળ હોય છે. તેથી અહીં પદાર્થની ઝડપ અચળ રહે છે તેમ કહેવાય.

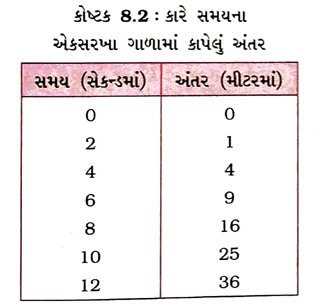
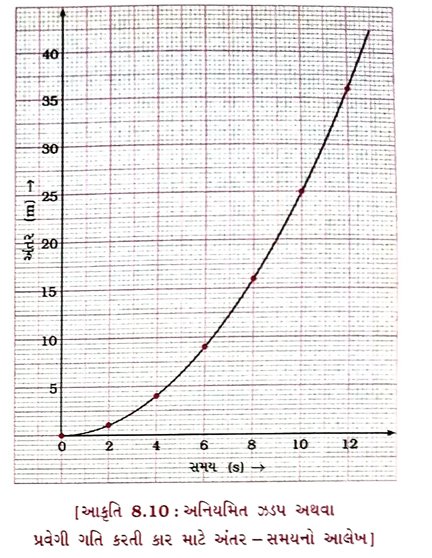
પ્રશ્ન 38. પ્રવેગી ગતિ માટે એક યોગ્ય ઉદાહરણ લઈને અંતર – સમયનો આલેખ દોરો અને ટૂંકમાં સમજાવો. [3 ગુણ]

ઉત્તર :

→ કોષ્ટક 8.2માં આપેલ સમય અને તેને અનુરૂપ અંતરનાં મૂલ્યોને આધારે કા૨ની ગતિ માટે અંતર – સમયનો આલેખ આકૃતિ 8.10માં દર્શાવ્યો છે.

→ અહીં આલેખનો આકાર સુરેખા નથી, જે નિયમિત ગતિ માટે હોય છે.

→ આલેખનો આકાર દર્શાવે છે કે કા૨ે કાપેલ અંતર અને તેને અનુરૂપ સમય વચ્ચે અરેખીય સંબંધ છે.

આમ, ઉપરોક્ત આલેખ અનિયમિત ઝડપ માટેનો છે. સમય વધતાં ઝડપ પણ વધે છે. તેથી તે પ્રવેગી ગતિ માટેનો પણ આલેખ છે.

પ્રશ્ન 39. પદાર્થ નિયમિત ઝડપે અને અનિયમિત ઝડપે ગતિ કરતો હોય, તો તેના માટે અંતર – સમયના આલેખો દોરો અને સવિસ્તાર સમજાવો. [4 ગુણ]

ઉત્તર : જુઓ પ્રશ્ન 37 અને 38ના ઉત્તર.

પ્રશ્ન 40. અંતર – સમયના આલેખોના ઉપયોગો જણાવો. [3 ગુણ]

ઉત્તર : (1) અંતર – સમયના આલેખ પરથી પદાર્થની ગતિના પ્રકાર વિશે જાણી શકાય છે. એટલે કે પદાર્થની ગતિ નિયમિત છે કે અનિયમિત તે જાણી શકાય છે.

(2) અંતર – સમયના આલેખ પરથી આપેલ સમયગાળાના કોઈ પણ સમયે ગતિ કરતા પદાર્થનું અંદાજિત સ્થાન નક્કી કરી શકાય છે તેમજ જે-તે સ્થાન પર પદાર્થ કયા સમયે પહોંચ્યો હશે તે પણ કહી શકાય છે.

(3) અંતર – સમયના આલેખમાં મળતી સુરેખાના ઢાળ પરથી નિયમિત ગતિ કરતા પદાર્થની ઝડપ (વેગનું મૂલ્ય) શોધી શકાય છે.

(4) એક જ આલેખપત્ર પર દોરેલા અંતર – સમયના આલેખ પરથી નિયમિત ઝડપથી ગતિ કરતા પદાર્થોની ઝડપની સરખામણી કરી શકાય છે.

(5) એક જ આલેખપત્ર પર દોરેલા અંતર–સમયના આલેખ પરથી એક જ સીધા રસ્તા પર જુદી જુદી ઝડપથી ગતિ કરતા બે પદાર્થો એકબીજાને ક્યાં અને ક્યારે મળશે તે પણ નક્કી કરી શકાય છે.

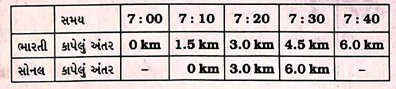
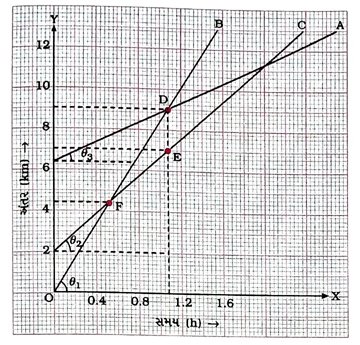
પ્રશ્ન 41. ભારતી અને સોનલ 6km દૂર આવેલી શાળાએ પોતપોતાની સાઇકલ લઈને નિયમિત ગતિએ જાય છે. ભારતી સવારે 7:00 વાગ્યે જ્યારે સોનલ 7:10 વાગ્યે શાળાએ જવા નીકળે છે. બંને એક જ રસ્તા પર થઈને છે. જુદા જુદા સમયે તેમણે કાપેલાં અંતર વિશેની માહિતી કોષ્ટક છે 8.3માં દર્શાવ્યા મુજબ છે : [4 ગુણ] 

(1) એક જ આલેખપેપર પર બંનેની સાઇકલની ગતિ માટે અંતર – સમયનો આલેખ દોરો.

(2) આલેખ પરથી નક્કી કરો કે સોનલ અને ભારતી બંનેમાંથી કોની ઝડપ વધારે છે?

(3) સોનલ અને ભારતી રસ્તા પર ક્યા સમયે અને ઘરથી કેટલા અંતરે એકબીજાને મળશે?

(4) સોનલ અને ભારતી બંનેમાંથી કોણ પહેલાં શાળાએ પહોંચશે?

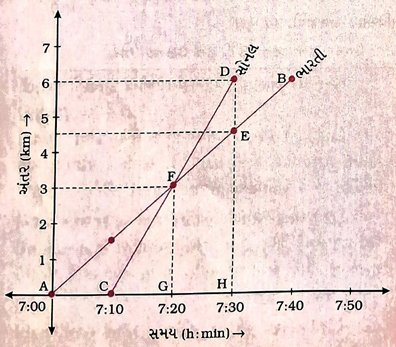
ઉત્તર : એક જ આલેખપેપર પર ભારતી અને સોનલની સાઇક્લની ગતિ માટે અંતર – સમય (x – t)નો આલેખ નીચેની આકૃતિ 8.11માં દર્શાવ્યા મુજબ મળશે :

આ આલેખ પરથી આપણને નીચે મુજબની માહિતી મળશે :

(1) ભારતી અને સોનલ બંને અલગ અલગ સમયે શાળાએ જવા નીકળે છે તેમજ અલગ અલગ સમયે શાળાએ પહોંચે છે.

(2) બંને આલેખો સુરેખા સ્વરૂપે મળે છે, જેથી બને નિયમિત ગતિએ સાઇકલ ચલાવે છે.

(3) બંને સુરેખાના ઢાળ શોધવાથી તેમની ઝડપનો ખ્યાલ આવે છે. આલેખ પરથી ઢાળ શોધો.

(4) આલેખ પરથી સ્પષ્ટ છે કે બંને રેખાઓ એકબીજાને F બિંદુ આગળ છેદે છે અને તેના યામ (7 : 20,3 km) છે. એટલે કે બંને જણા ઘરથી 3 km દૂર બરાબર 7 : 20 ક્લાકે એકબીજાને મળે છે. ત્યારબાદ સોનલ ભારતી કરતાં આગળ નીકળી જાય છે.

(5) સોનલ 7 : 30 વાગ્યે શાળાએ પહોંચે છે, જ્યારે આ સમયે ભારતી શાળાથી 1.5 km દૂર છે.

(6) સોનલ અને ભારતીને શાળાએ પહોંચતા અનુક્રમે 20 min અને 40 min લાગે છે.

8.4.2 વેગ – સમયના આલેખો

પ્રશ્ન 42. સુરેખ પથ પર એક દિશામાં નિયમિત વેગથી ગતિ કરતી કાર માટે વેગ – સમયનો આલેખ દોરો અને તેના પરથી કારે કાપેલું અંતર કેવી રીતે શોધી શકાય છે તે સમજાવો. [3 ગુણ]

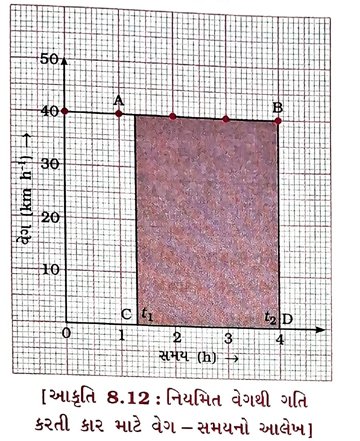
ઉત્તર :

આકૃતિ 8.12માં સુરેખ પથ પર એક દિશામાં અચળ વેગથી (40 km h−1થી) ગતિ કરતી એક કાર માટેનો છ– દર્શાવ્યો છે. –tનો આલેખ

અત્રે વેગ – સમયના આલેખની ઊંચાઈ સમય સાથે બદલાતી નથી. તે X-અક્ષ(t-અક્ષ)ને સમાંતર સુરેખા છે.

→ અચળ વેગથી ગતિ કરતા પદાર્થ માટે સમય અને વેગનો ગુણાકાર સ્થાનાંતર (સદિશ રાશિ) આપે છે.

→ વેગ – સમયના આલેખ તથા સમય-અક્ષ વડે ઘેરાતા વિસ્તારનું (બંધગાળાનું) ક્ષેત્રફળ સ્થાનાંતરનું મૂલ્ય આપે છે.

→ અહીં, કાર સુરેખ પથ પર એક દિશામાં અચળ વેગથી ગતિ કરે છે. તેથી t₁ અને t₂ સમયની વચ્ચે કા૨ે કાપેલું અંતર, કારે કરેલા સ્થાનાંતરના મૂલ્ય જેટલું હશે.

→ હવે, t₁ અને t₂ સમયની વચ્ચે કા૨ે કાપેલું અંતર શોધવા માટે t₁ અને t₂ સમયનાં મૂલ્યો ૫૨થી આલેખ પર લંબ દોરો.

→ વેગ 40 km h⁻¹ ને ઊંચાઈ (AC) અથવા (BD) વડે અને સમયના તફાવત (t₂ – t₁)ને લંબાઈ (CD) અથવા (AB) વડે દર્શાવેલ છે.

∴ (t₂ – t₁) સમયગાળામાં કા૨ે કાપેલું અંતર,

s = AC × CD

= [(40 km h⁻¹) × (t₂ − t₁) h]

= 40 (t₂ – t₁) km = લંબચોરસ ABDCનું ક્ષેત્રફળ

પ્રશ્ન 43. સુરેખ પથ પર એક દિશામાં અચળ પ્રવેગી ગતિ કરતી કાર માટે વેગ – સમયનો આલેખ દોરો અને તેના પરથી કારે કાપેલું અંતર કેવી રીતે શોધી શકાય છે તે સમજાવો. [3 ગુણ]

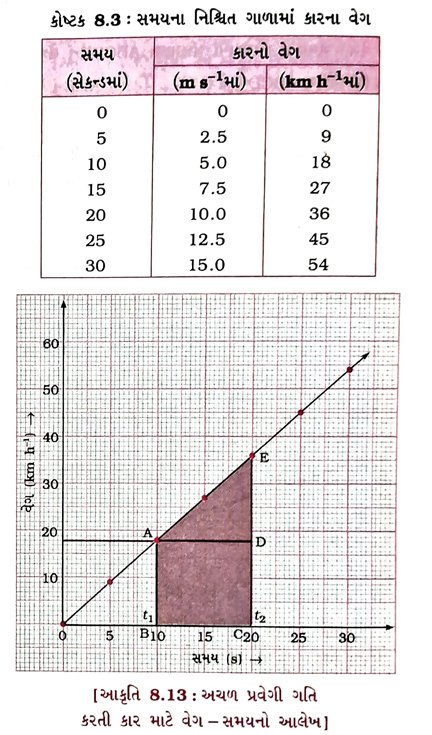
ઉત્તર : એક કાર સુરેખ પથ પર એક દિશામાં ગતિ શરૂ કરે છે. કારનો ડ્રાઇવર, કારના એન્જિનની ગુણવત્તા અને શક્તિની કસોટી કરવા માંગે છે. ડ્રાઇવરની બાજુમાં બેઠેલી વ્યક્તિ દર 5 સેકન્ડે કારના સ્પીડોમિટરની મદદથી કારની ઝડપ (અહીં વેગ) નોંધે છે.

→ કારનો વેગ km h⁻¹ માં અને m s⁻¹ માં કોષ્ટક 8,3માં દર 5 સેકન્ડે દર્શાવ્યો છે.

→ કોષ્ટક 8.3માં આપેલ સમય અને તેને અનુરૂપ વેગ(km h⁻¹માં)નાં મૂલ્યોને આધારે કારની ગતિ માટે વેગ – સમયનો આલેખ આકૃતિ 8.13માં દર્શાવ્યો છે.

→ આલેખનો આકાર દર્શાવે છે કે કારનો વેગ એકસરખા પ્રમાણમાં એકસરખા સમયગાળા દરમિયાન વધે છે, જે કારની અચળ પ્રવેગી ગતિનું સૂચન કરે છે.

આમ, દરેક અચળ પ્રવેગી ગતિ કરતા પદાર્થ માટે વેગ – સમયનો આલેખ સુરેખા હોય છે.

→ હવે, વેગ – સમયના આલેખ તથા સમય-અક્ષ વડે ઘેરાતા વિસ્તારનું (બંધગાળાનું) ક્ષેત્રફળ આપેલ સમયગાળા માટે સ્થાનાંતરનું મૂલ્ય આપે છે.

→ પણ અહીં કાર સુરેખ પથ પર એક દિશામાં અચળ પ્રવેગી ગતિ કરે છે. તેથી આ સ્થાનાંતરનું મૂલ્ય કારે આપેલ સમયગાળા દરમિયાન કાપેલા અંતરનું મૂલ્ય દર્શાવે છે.

→ (t₂ − t₁) સમયગાળા દરમિયાન કારે કાપેલું અંત૨ શોધવા માટે t₁ અને t₂ સમયનાં મૂલ્યો પરથી આલેખ ૫૨ લંબ દોરો.

→ અત્રે કાર સુરેખ પથ પર અચળ પ્રવેગી ગતિ કરે છે. તેથી (t₂ – t₁) સમયગાળા દરમિયાન કા૨ે કાપેલું અંતર,

s = વેગ – સમયના આલેખમાં બંધગાળા ABCDEનું ક્ષેત્રફળ =

= (લંબચોરસ ABCDનું ક્ષેત્રફળ) + (ત્રિકોણ ADEનું ક્ષેત્રફળ)

= (AB × BC) + 1/2 (AD × DE)

પ્રશ્ન 44, કાર અચળ વેગથી અને અચળ પ્રવેગથી ગતિ કરતી હોય, તો તેના માટે વેગ – સમયના આલેખો દોરો અને સવિસ્તર સમજાવો. [4 ગુણ]

ઉત્તર : જુઓ પ્રશ્ન 42 અને 43નો ઉત્તર.

પ્રશ્ન 45. નિયમિત પ્રતિપ્રવેગી ગતિ (Uniformly retarded motion) માટેનો વેગ – સમયનો આલેખ દોરો અને ટૂંકમાં સમજાવો. [3 ગુણ]

ઉત્તર :

→ અહીં ઋણ નિશાની સમય સાથે વેગમાં ઘટાડો થાય છે તેમ સૂચવે છે.

→ પદાર્થના વેગમાં 20/6 m s⁻¹ જેટલો ઘટાડો દર સેકન્ડે થાય છે અર્થાત્ એકસરખા સમયગાળામાં વેગમાં થતો ઘટાડો એકસરખો છે, જે નિયમિત પ્રતિપ્રવેગી ગતિ માટેની લાક્ષણિકતા છે.

પ્રશ્ન 46. અનિયમિત પ્રવેગી ગતિ માટે વેગ – સમયનો આલેખ દોરો અને તેને ટૂંકમાં સમજાવો. [2 ગુણ]

ઉત્તર :

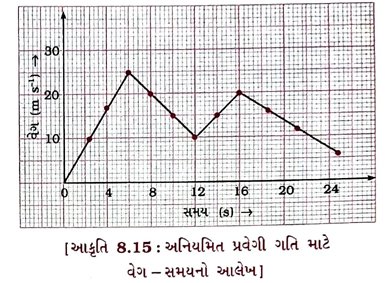
આકૃતિ 8.15માં અનિયમિત પ્રવેગી ગતિ કરતા પદાર્થનો વેગ – સમયનો આલેખ દર્શાવ્યો છે.

→ પ્રારંભમાં t = 0 સમયે પદાર્થનો વેગ શૂન્ય છે.

→ સમય વધતાં વેગ નિયમિત રીતે t = 6 s સુધી વધીને t = 6 સેકન્ડે મહત્તમ બને છે. (લગભગ 25 m s⁻¹)

→ ફરીથી સમય વધતાં વેગ નિયમિત રીતે ઘટે છે, t = 12 સેકન્ડે તે લગભગ 10 m s⁻¹ થાય છે.

→ સમય વધતાં તે ફરી પાછો વધે છે. આમ ચાલ્યા કરે છે.

આમ, અનિયમિત રીતે પદાર્થના વેગમાં વધારો-ઘટાડો થયા કરે છે. પદાર્થની આ પ્રકારની ગતિને અનિયમિત પ્રવેગી ગતિ કહે છે.

અનિયમિત પ્રવેગી ગતિ કરતા પદાર્થો માટે વેગ – સમયના આલેખો સુરેખા હોતા નથી, પણ તેમનો આકાર સુરેખા સિવાયનો કોઈ પણ હોય છે.

પ્રશ્ન 47. ગતિમાન પદાર્થ માટે વેગ – સમયના આલેખના ઉપયોગો જણાવો. [3 ગુણ]

ઉત્તર : ( 1 ) વેગ – સમયના આલેખ પરથી ગતિમાન પદાર્થ નિયમિત ગતિ કરે છે કે અનિયમિત તે જાણી શકાય છે.

( 2 ) વેગ – સમયના આલેખ પરથી પદાર્થના વેગના મૂલ્યમાં થતા ફેરફારો વિશે જાણકારી મેળવી શકાય છે. આલેખનો ઢાળ પ્રવેગ દર્શાવે છે. આ પરથી પદાર્થ પ્રવેગી અથવા પ્રતિપ્રવેગી ગતિ કરે છે તે જાણી શકાય છે.

( 3 ) વેગ – સમયના આલેખ પરથી આલેખ દ્વારા ઘેરાતા પ્રદેશનું ક્ષેત્રફળ શોધવાથી આપેલ સમયગાળા દરમિયાન પદાર્થે છે. કાપેલું અંતર શોધી શકાય છે.

( 4 ) એક જ આલેખપત્ર પર બે જુદા જુદા પદાર્થો માટે વેગ – સમયના આલેખ પરથી તે બે પદાર્થોના વેગની સરખામણી કરી શકાય છે.

Intext પ્રશ્નોત્તર

પ્રશ્ન 48. કોઈ પદાર્થની નિયમિત અને અનિયમિત ગતિ માટે અંતર – સમયના આલેખનો આકાર કેવો હોય છે? [1 ગુણ]

ઉત્તર : નિયમિત ગતિ માટે અંતર – સમયનો આલેખ સુરેખા હોય છે, જે સમય-અક્ષ (X-અક્ષ) સાથે ઢળતો હોય છે, અર્થાત્ આલેખના ઢાળનું કંઈક મૂલ્ય (શૂન્ય અને અનંત નહિ) હોય છે.

અનિયમિત ગતિ માટે અંતર – સમયનો આલેખ સુરેખ હોતો નથી.

પ્રશ્ન 49. કોઈ પદાર્થની ગતિની બાબતમાં તમે શું કહી શકો જેનો અંતર – સમયનો આલેખ સમયની અક્ષને સમાંતર રેખા હોય? [1 ગુણ]

ઉત્તર : તે પદાર્થ સ્થિર હશે, કારણ કે સમયની દરેક ક્ષણે પદાર્થનું અંતર બદલાતું નથી.

પ્રશ્ન 50. કોઈ પદાર્થની ગતિની બાબતમાં તમે શું કહી શકો જેનો ઝડપ – સમયનો આલેખ સમયની અક્ષને સમાંતર રેખા હોય? [1 ગુણ]

ઉત્તર : પદાર્થ અચળ ઝડપે ગતિ કરતો હશે, કારણ કે સમયના દરેક ક્ષણે પદાર્થની ઝડપ બદલાતી નથી.

પ્રશ્ન 51. વેગ – સમયના આલેખની નીચે ઘેરાયેલ ક્ષેત્રફળનું માપ કઈ ભૌતિક રાશિ દર્શાવે છે? [1 ગુણ]

ઉત્તર : આપેલ સમયગાળામાં પદાર્થના સ્થાનાંતરનું મૂલ્ય દર્શાવે છે.

જો પદાર્થ સુરેખ પથ પર એક જ દિશામાં ગતિ કરતો હોય, તો તે પદાર્થ દ્વારા કપાયેલું અંતર સૂચવે છે.

8.5 આલેખીય રીત વડે ગતિ(નિયમિત પ્રવેગી ગતિ)નાં સમીકરણો

પ્રશ્ન 52. ગતિનાં સમીકરણો અથવા નિયમિત પ્રવેગી ગતિનાં સમીકરણો કોને કહે છે? તે સમીકરણો જણાવો. [2 ગુણ]

ઉત્તર : જ્યારે પદાર્થ સુરેખ પથ પર અચળ પ્રવેગી ગતિ કરે છે ત્યારે તેના વેગ, પ્રવેગ અને આપેલ સમયગાળા દરમિયાન તેણે કાપેલા અંતરને એક્બીજા સાથે સાંકળતાં સમીકરણોને ગતિનાં સમીકરણો કહે છે. ગતિનાં સમીકરણો નીચે મુજબ છે :

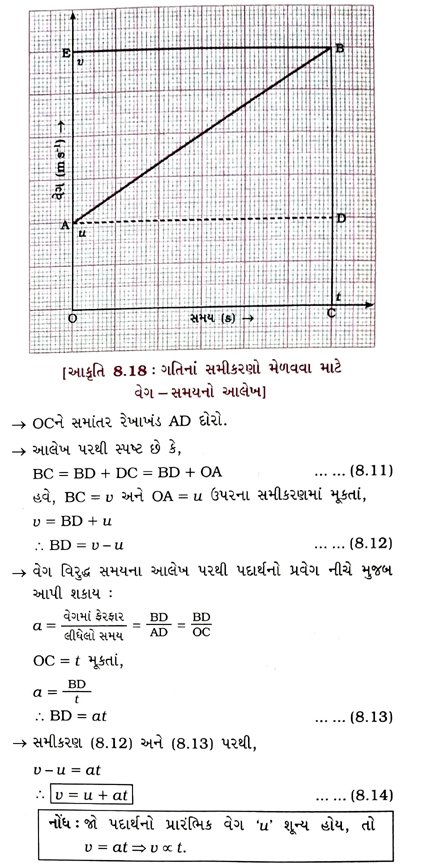
(1) વેગ અને સમય વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ,

v = u + at

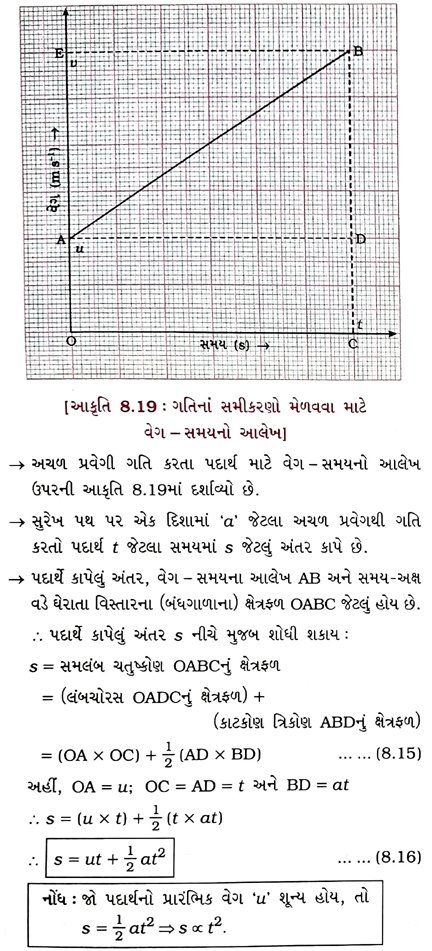
(2) અંતર અને સમય વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ,

s = ut + 1/2at²

(3) અંતર અને વેગ વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ,

2as = v² – u²

ઉપરોક્ત સમીકરણોમાં,

u = અચળ પ્રવેગી ગતિ કરતા પદાર્થનો પ્રારંભિક વેગ

v = અંતિમ વેગ

a = પ્રવેગ (અચળ)

t = સમય

s = t સમયમાં પદાર્થે કાપેલું અંતર

8.5.1 વેગ અને સમય વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ

પ્રશ્ન 53. સુરેખ પથ પર અચળ પ્રવેગી ગતિ માટે વેગ અને સમય વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ આલેખની રીતે મેળવો. [3 ગુણ]

અથવા

આલેખની રીતે સુરેખ પથ પર થતી અચળ પ્રવેગી ગતિનું સમીકરણ v = u + at મેળવો.

ઉત્તર : અચળ પ્રવેગી ગતિ કરતા પદાર્થ માટે વેગ – સમયનો આલેખ આકૃતિ 8.18માં દર્શાવ્યો છે.

→ આલેખ પરથી સ્પષ્ટ છે કે પદાર્થનો પ્રારંભિક વેગ u (A બિંદુ પાસે) છે અને તે t સમયમાં વધીને છ જેટલો (B બિંદુ પાસે) થાય છે.

→ વેગ ‘a‘ જેટલા અચળ દરે વધે છે.

→ આલેખ પરના B બિંદુ આગળથી સમય-અક્ષ અને વેગ-અક્ષ પર અનુક્રમે BC અને BE લંબ દોરેલા છે. તેથી OA પ્રારંભિક વેગ (u) દર્શાવે છે, BC અંતિમ વેગ (u) દર્શાવે છે અને OC સમય (t) દર્શાવે છે.

8.5.2 સ્થાન (અથવા અંતર) અને સમય વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ

પ્રશ્ન 54. સુરેખ પથ પર અચળ પ્રવેગી ગતિ માટે સ્થાન (અંતર) અને સમય વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ આલેખની રીતે મેળવો. [3 ગુણ]

અથવા

આલેખની રીતે સુરેખ પથ પર થતી અચળ પ્રવેગી ગતિનું સમીકરણ s = ut + 1/2at² મેળવો.

ઉત્તર :

8.5.3 સ્થાન (અથવા અંતર) અને વેગ વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ

પ્રશ્ન 55. સુરેખ પથ પર અચળ પ્રવેગી ગતિ માટે સ્થાન (અંતર) અને વેગ વચ્ચેનો સંબંધ દર્શાવતું સમીકરણ આલેખની રીતે મેળવો. [3, ગુણ]

અથવા

આલેખની રીતે સુરેખ પથ પર થતી અચળ પ્રવેગી ગતિનું સમીકરણ 2as = v² – u² મેળવો. 

ઉત્તર :

પ્રશ્ન 56. આલેખની મદદથી અચળ પ્રવેગી ગતિનાં સમીકરણો મેળવો. [4 ગુ]

ઉત્તર : જો પ્રશ્ન 53, 54 અને 55નો ઉત્તર,

Intext પ્રશ્નોત્તર

પ્રશ્ન 57 એક બસ સ્થિર સ્થિતિમાંથી ગતિની શરૂઆત કરે છે તથા 2 min સુધી 0.1 m s^-2 ના અચળ પ્રવેગથી ગતિ કરે છે, તો

(a) પ્રાપ્ત કરેલ ઝડપ અને (b) તેણે કાપેલ અંતર શોધો. [2 ગુણ]

ઉકેલ :

પ્રશ્ન 58. એક ટ્રેન 90 km h⁻¹ની ઝડપથી ગતિ કરી રહી છે. બ્રેક મારતાં તેમાં – 0.5 m s⁻²નો અચળ પ્રવેગ ઉત્પન્ન થાય છે. ટ્રેન સ્થિર સ્થિતિમાં આવે તે પહેલાં કેટલું અંતર કાપશે? [2 ગુણ]

ઉકેલ :

પ્રશ્ન 59. એક ટ્રૉલી ઢોળાવ ધરાવતી સપાટી પર 2 m s⁻²ના પ્રવેગથી નીચે તરફ ગતિ કરી રહી છે. ગતિની શરૂઆત બાદ 3 sના અંતે તેનો વેગ કેટલો હશે? [1 ગુણ]

ઉકેલ : અત્રે, u = 0; a = 2 cm s^-2; t = 3 s; v = ?

v = u + at

= 0 + (2 cm s^-2) × (3 s) = 6 cm s^-1

આમ, ટ્રૉલી સ્થિર સ્થિતિમાંથી ઢોળાવ પરથી નીચે તરફ ગતિ કરે ત્યારે 3 sના અંતે તેનો વેગ 6 cm s^-1 હશે.

પ્રશ્ન 60. એક રેસિંગ કારનો અચળ પ્રવેગ 4 ms^-2 છે. ગતિની શરૂઆત બાદ 10sના અંતે તેણે કેટલું અંતર કાપેલ હશે? [1 ગુણ)

ઉકેલ :

આમ, રેસિંગ કારે સ્થિર સ્થિતિમાંથી ગતિની શરૂઆત કર્યા બાદ 10 sના અંતે 200 m અંતર કાપેલ હશે.

પ્રશ્ન 61. એક પથ્થરને ઊદિશામાં 5 m s⁻¹ના વેગથી ફેંક્વામાં આવે છે. જો ગતિ દરમિયાન પથ્થરનો અધોદિશામાં પ્રવેગ 10 m s^-2 હોય, તો પથ્થર કેટલી ઊંચાઈ પ્રાપ્ત કરશે તથા તેને ત્યાં પહોંચતાં કેટલો સમય લાગશે? [3 ગુણ]

ઉકેલ :

આમ, પથ્થર 1.25 m જેટલી મહત્તમ ઊંચાઈ પ્રાપ્ત કરશે અને ત્યાં પહોંચવા માટે 0.5 s જેટલો સમય લેશે.

8.6 નિયમિત વર્તુળમય ગતિ

પ્રશ્ન 62. નિયમિત વર્તુળમય ગતિ એટલે શું? તેનાં બે ઉદાહરણ આપો. [2 ગુણ]

ઉત્તર : જો કોઈ પદાર્થ અચળ ઝડપે વર્તુળાકાર પથ પર ગતિ કરતો હોય, તો તે નિયમિત વર્તુળમય ગતિ કરે છે તેમ કહેવાય.

ઉદાહરણ : (1) ઘડિયાળના સેકન્ડ કાંટાનો છેડો (tip), ઘડિયાળના ડાયલ પર નિશ્ચિત સમયમાં વર્તુળગતિ કરતો હોય છે. તેથી તેની ગતિ નિયમિત વર્તુળમય ગતિ છે.

(2) ચંદ્ર પૃથ્વીનો કુદરતી ઉપગ્રહ છે. ચંદ્ર પૃથ્વીની આસપાસ નિશ્ચિત સમયમાં વર્તુળગતિ કરે છે. તેથી તેની ગતિ નિયમિત વર્તુળમય ગતિ છે.

સ્વાધ્યાયના પ્રશ્નોત્તર

(1) એક ઍથ્લેટ 200 m વ્યાસ ધરાવતા વર્તુળાકાર પથ પર એક ચક્કર 40 sમાં પૂરું કરે છે. 2 min 20 s બાદ તેણે કેટલું અંતર કાપ્યું હશે તથા તેનું સ્થાનાંતર કેટલું હશે? [3 ગુણ]

ઉકેલ : વર્તુળાકાર માર્ગનો વ્યાસ = 200 m

∴ ત્રિજ્યા r = 100 m

વર્તુળ પથ પર એક ચક્કર પૂર્ણ કરવા લાગતો સમય = 40 s

∴ 2 minute અને 20 s = 140 sમાં ઍથ્લેટ 140/40 = 3.5 ચક્કર પૂર્ણ કરશે.

→ 1 ચક્કર પૂર્ણ થતા કાપેલું અંતર = વર્તુળ પથનો પરિઘ

= 2πr

∴ 3.5 ચક્કર પૂર્ણ થતા કાપેલું અંતર = 2πr × 3.5

= 2 × 22/7 × 100 × 3.5

= 2200 m

→ 3.5 ચક્કર પૂર્ણ થતા ઍથ્લેટ વર્તુળ પથ પર વ્યાસના બીજા છેડે હશે.

∴ ઍથ્લેટનું સ્થાનાંતર = વર્તુળનો વ્યાસ = 2r = 200 m

આમ, અંતર = 2200 m અને સ્થાનાંતર = 200 m

(2) 300 mના સીધા રસ્તા પર જૉસેફ જૉગિંગ કરતો કરતો 2 min 30 sમાં એક છેડા Aથી બીજા છેડા B સુધી પહોંચે છે. ત્યાંથી પાછો ફરી 1 મિનિટમાં 100 m પાછળ રહેલા બિંદુ C પર પહોંચે છે. જૉસેફની સરેરાશ ઝડપ અને સરેરાશ વેગ ( ૩ ) A છેડાથી B છેડા સુધી તથા ( 5 ) A છેડાથી C છેડા સુધી કેટલો હશે? [3 ગુણ]

ઉકેલ :

(3) અબ્દુલ ગાડી દ્વારા શાળાએ જતી વખતે સરેરાશ ઝડપ 20 km h⁻¹ માપે છે. તે જ રસ્તા પર પાછા ફરતી વખતે ટ્રાફિક ઓછો હોવાને કારણે તે 30 km h⁻¹ સરેરાશ ઝડપ માપે છે. અબ્દુલની સમગ્ર મુસાફરી દરમિયાન સરેરાશ ઝડપ કેટલી હશે? [3 ગુણ]

ઉકેલ : ધારો કે, ઘરથી શાળાનું અંતર x km છે.

(4) તળાવમાં સ્થિર અવસ્થામાં રહેલી એક મોટરબોટ સુરેખ પથ પર 3.0 m s⁻²ના અચળ પ્રવેગથી 8.0 s સુધી ગતિ કરે છે. આ સમયગાળામાં મોટરબોટ કેટલી દૂર ગઈ હશે? [1 ગુણ]

ઉકેલ :

(5) 52 km h^-1ની ઝડપથી ગતિ કરતી કારનો ડ્રાઇવર બ્રેક મારતાં, કારમાં ગતિની વિરુદ્ધ દિશામાં અચળ પ્રવેગ ઉત્પન્ન થાય છે. કાર 5 sમાં અટકી જાય છે. બીજો ડ્રાઇવર 34 km h⁻¹ની ઝડપથી ગતિ કરતી બીજી કાર પર ધીમેથી બ્રેક લગાડતાં તે 10 s માં અટકે છે. એક જ આલેખ(ગ્રાફ)પેપર પર ઝડપ વિરુદ્ધ સમયનો આલેખ બંને કાર માટે દોરો. બ્રેક લગાડ્યા બાદ બંનેમાંથી કઈ કાર વધારે દૂર સુધી જશે? [3 ગુણ]

ઉકેલઃ

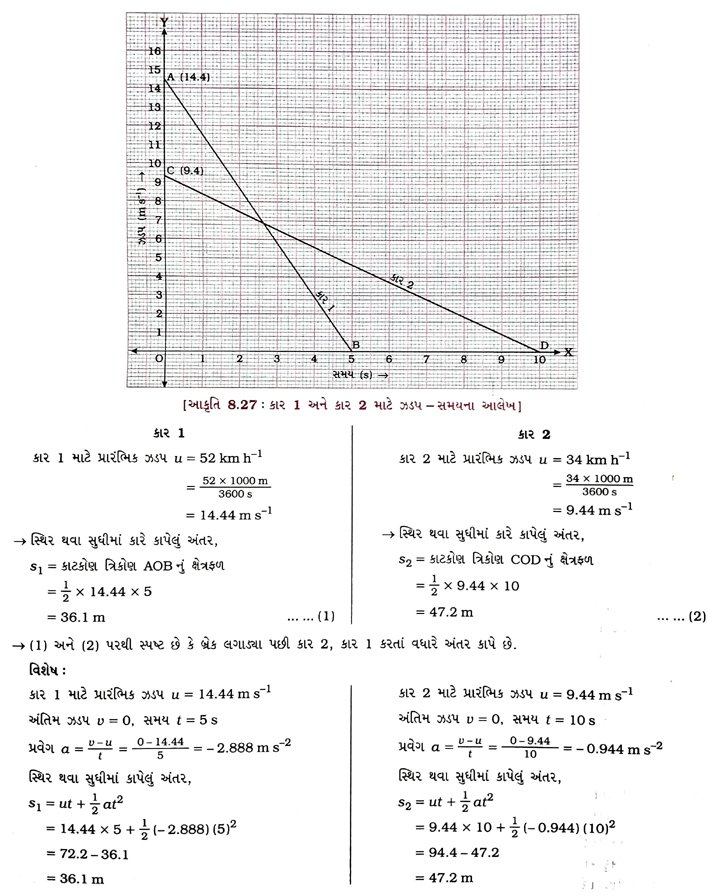
(6) આકૃતિ 8.28માં ત્રણ વાહનો A, B અને C માટે અંતર – સમયનો આલેખ દર્શાવેલ છે. આલેખનો અભ્યાસ કરી નીચેના પ્રશ્નોનો ઉત્તર આપો : [4 ગુણ]

(a) ત્રણેયમાંથી સૌથી વધારે ઝડપથી કોણ ગતિ કરે છે?

(b) શું. ત્રણેય કોઈ સમયે રોડ પરના એક જ બિંદુએ હશે?

(c) જ્યારે B, A પાસેથી પસાર થાય ત્યારે C કેટલે દૂર હશે?

(d) જ્યારે B, C પાસેથી પસાર થાય તે સમય દરમિયાન તેણે કેટલું અંતર કાપ્યું હશે?

ઉકેલ :

(a) ઝડપ = અંતર વિરુદ્ધ સમયના આલેખનો ઢાળ = tan θ

અત્રે, આપેલ આકૃતિ પરથી θ₁ > θ₂ > θ₃

∴ tan θ₁ > tan θ₂ > tan θ₃ થાય.

∴ (Bની ઝડપ) > (Cની ઝડપ) > (Aની ઝડપ)

∴ B વાહન સૌથી વધુ ઝડપે ગતિ કરે છે.

(b) રોડ પર ત્રણેય વાહનો એકસાથે ત્યારે જ જોવા મળે કે જ્યારે ત્રણેય વાહનોના આનુષાંગિક અંતરો અને સમયનાં મૂલ્યો એકસમાન હોય, એટલે કે અંતર – સમયના આલેખો ત્રણેય વાહનો માટે એક સામાન્ય બિંદુ આગળ છે. પણ આપેલ આકૃતિમાં આવું એક પણ સામાન્ય છેદનબિંદુ નથી. તેથી ત્રણેય વાહનો એકબીજાને એક સામાન્ય બિંદુ પાસે મળશે નહીં.

(c) આપેલ આકૃતિ પરથી સ્પષ્ટ છે કે વાહન B, વાહન Aને D બિંદુ આગળ પસાર કરે છે. આ વખતે વાહન C, E બિંદુ પાસે હશે, જેનો Y-યામ 7 km છે.

∴ જ્યારે B, A પાસેથી પસાર થશે ત્યારે C ઊગમબિંદુથી 7 km અંતરે હશે. (C એ કાપેલું અંતર (7 – 2) km = 5 km)

(d) આપેલ આકૃતિ પરથી સ્પષ્ટ છે કે B, Cને F બિંદુ આગળ પસાર કરે છે. Fબિંદુનું ઊગમબિંદુથી અંતર 4.5 km છે.

∴ જ્યારે B, C પાસેથી પસાર થશે ત્યારે B ઊગમબિંદુથી 4.5 km અંતરે હશે. (B એ કાપેલું અંતર 4.5 km)

(7) 20 mની ઊંચાઈ પરથી એક દડાને નીચે પડવા દેવામાં આવે છે. જો તેનો વેગ 10 m s⁻²ના નિયમિત પ્રવેગથી વધતો હોય, તો તે કેટલા વેગથી જમીન સાથે અથડાશે? કેટલા સમય બાદ તે જમીન સાથે અથડાશે? [3 ગુણ]

ઉકેલ :

આમ, દડો જમીનને 20 m s⁻¹ જેટલા વેગથી અથડાશે અને ગતિની શરૂઆત કર્યા બાદ 2 s પછી જમીનને અથડાશે.

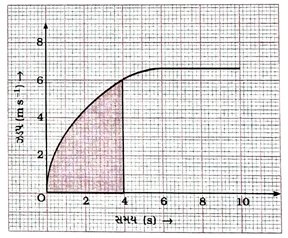
(8) આકૃતિ 8.29માં ઝડપ – સમયનો આલેખ એક ગતિ કરતી કાર માટે દર્શાવેલ છે.

(a) પ્રથમ 4 sમાં કાર કેટલું અંતર કાપશે? આ સમયગાળા દરમિયાન કાર દ્વારા કાપેલ અંતરને આલેખમાં છાયાંકિત કરો.

(b) આલેખનો કયો ભાગ કારની અચળ ગતિ દર્શાવે છે? [3 ગુણ]

ઉકેલ :

(a) આપેલ આલેખ પરથી …

સમય-અક્ષ પર 10 અતિ નાના વિભાગ = 2 s

ઝડપ-અક્ષ પર 10 અતિ નાના વિભાગ = 2 m s⁻¹

∴ 10 × 10 = 100 અતિ નાના ચોરસ

= 2 s × 2 m s⁻¹ = 4m

→ પ્રથમ 4 s દરમિયાન ઝડપ – સમયના આલેખ અને સમય-અક્ષ વડે ઘેરાતા વિસ્તારનું (બંધગાળાનું) ક્ષેત્રફળ = 400 નાના ચોરસ (લગભગ).

અત્રે છાયાંકિત ભાગમાંના અતિ નાના ચોરસોની સંખ્યા ગણતી વખતે જે ચોરસ અડધા કે તેના કરતાં વધુ છાયાંકિત છે તેમને પૂર્ણ ચોરસ તરીકે ગણ્યાં છે, જ્યારે જે અતિ નાના ચોરસ અડધાથી ઓછા છાયાંકિત છે તેમને ગણતરીમાં લીધા નથી.

હવે, અતિ નાના ચોરસોની સંખ્યા → અનુરૂપ અંતર

100 :: 4m

400 :: (?)

∴ પ્રથમ ચાર સેકન્ડ દરમિયાન કારે કાપેલું અંતર

= 400×4m/100 = 16.0 m (લગભગ)

(b) અચળ ગતિમાં પદાર્થની ઝડપ સમય સાથે અચળ રહે છે.

∴ t = 6 s થી લઈને t = 10 s સુધીના આલેખના ભાગમાં કાર અચળ ગતિ કરશે.

(9) નીચેના પૈકી કઈ પરિસ્થિતિ શક્ય છે તથા દરેકનાં ઉદાહરણ આપો :

(a) કોઈ પદાર્થ કે જેનો પ્રવેગ અચળ પણ વેગ શૂન્ય હોય.

(b) કોઈ પદાર્થ કે જે નિશ્ચિત દિશામાં ગતિ કરતો હોય તથા તેનો પ્રવેગ લંબ દિશામાં હોય. [3 ગુણ]

ઉકેલ :

(a) અમુક ઊંચાઈએથી મુક્ત પતન કરતો પદાર્થ

(મુક્ત પતન કરતા પદાર્થનો પ્રારંભિક વેગ (u) શૂન્ય હોય છે, પણ તેનો પ્રવેગ 9.8 m/s2 જેટલો અચળ હોય છે.)

(b) નિયમિત વર્તુળમય ગતિ કરતો પદાર્થ

(નિયમિત વર્તુળમય ગતિ કરતા પદાર્થના કિસ્સામાં વર્તુળમાર્ગના જે-તે બિંદુ આગળ પદાર્થનો વેગ ત્યાં દોરેલ સ્પર્શકની દિશામાં હોય છે, પણ તેનો પ્રવેગ કેન્દ્રગામી (વર્તુળના કેન્દ્ર તરફની દિશામાં) હોય છે; અર્થાત્ પદાર્થનો વેગ અને પ્રવેગ પરસ્પર લંબ હોય છે.)

હેતુલક્ષી પ્રશ્નોત્તર

પ્રશ્ન 1. નીચેના પ્રશ્નોના એક શબ્દ કે એક વાક્યમાં (1થી 10 શબ્દોની મર્યાદામાં) ઉત્તર લખો : (પ્રત્યેકનો 1 ગુણ)

(1) ગતિમાન પદાર્થે એકમ સમયમાં કરેલા સ્થાનાંતરને શું કહે છે?

(2) વેગનો SI એકમ જણાવો.

(3) એકમ સમયમાં ગતિમાન પદાર્થના વેગમાં થતાં ફેરફારને શું કહે છે?

(4) જો કોઈ ગતિમાન પદાર્થનો અંતિમ વેગ, પ્રારંભિક વેગ કરત ઓછો હોય, તો તે કેવા પ્રકારની ગતિ કરતો હશે?

(5) નિયમિત ગતિ કરતા પદાર્થ માટે અંતર – સમયનો આલેખ કેવો મળે?

(6) નિયમિત વર્તુળમય ગતિ કરતો પદાર્થ પ્રવેગી ગતિ કરે છે કે નિયમિત વેગવાળી ગતિ કરે છે?

(7) શું ગતિમાન પદાર્થની સરેરાશ ઝડપ અશૂન્ય અને સરેરાશ વેગ શૂન્ય હોઈ શકે? ઉદાહરણ આપો.

(8) એક કાર સુરેખ માર્ગ ૫૨ એક દિશામાં ગતિ કરી રહી છે. કારની ઝડપ દર 5 મિનિટે 5 km h⁻¹ જેટલી એક્સરખી વધે છે. આ કાર માટે ગતિની કઈ ભૌતિક રાશિ અચળ હશે?

(9) 314m પરિઘવાળા વર્તુળાકાર પથ પર રમેશ એક ચક્ર પૂરું કરે છે. રમેશે કરેલું સ્થાનાંતર કેટલું?

(10) m s^-2 કઈ ભૌતિક રાશિનો એકમ છે?

(11) ઝડપ છ – સમય t ના આલેખ દ્વારા ઘેરાતા બંધગાળાનું ક્ષેત્રફળ દર્શાવતી રાશિનો SI એકમ કર્યો છે?

(12) પદાર્થ ગતિ કરે છે એમ ક્યારે કહેવાય?

(13) પદાર્થ નિયમિત ગતિ કરે છે એમ ક્યારે કહેવાય?

(14) વાહનનું ઓડોમિટર કઈ ભૌતિક રાશિનું માપન દર્શાવે છે?

(15) વાહનનું સ્પીડોમિટર કઈ ભૌતિક રાશિનું માપન દર્શાવે છે?

(16) ઋણ પ્રવેગનું ઉદાહરણ આપો. અથવા પ્રતિપ્રવેગી ગતિનું ઉદ્યહરણ આપો.

(17) પદાર્થ અનિયમિત ગતિ કરે છે તેમ ક્યારે કહેવાય?

(18) વેગ (સદિશ રાશિ) v–સમય t આલેખ અને સમય-અક્ષ વડે ઘેરાતા બંધગાળાનું ક્ષેત્રફળ શું દર્શાવે છે?

ઉત્તર :

(1) વેગ

(2) m s^-1

(3) પ્રવેગ

(4) પ્રતિપ્રવેગી

(5) સુરેખા

(6) પ્રવેગી

(7) હા; વર્તુળમય ગતિ કરતો પદાર્થ એક પરિભ્રમણ પૂર્ણ કરે ત્યારે તેની ઝડપ અશૂન્ય અને સરેરાશ વેગ શૂન્ય હોય છે.

(8) પ્રવેગ

(9) શૂન્ય

(10) પ્રવેગનો

(11) મીટર

(12) જ્યારે કોઈ એક પદાર્થ બીજા કોઈ પદાર્થની સાપેક્ષે સમય સાથે પોતાનું સ્થાન બદલે, ત્યારે તે પદાર્થ બીજા પદાર્થની સાપેક્ષમાં ગતિ કરે છે તેમ કહેવાય.

(13) જો કોઈ ગતિમાન પદાર્થ (એક દિશામાં) સમયના એકસ૨ખા ગાળામાં એકસરખું અંતર કાપતો હોય, તો તે પદાર્થ નિયમિત ગતિ કરે છે તેમ કહેવાય.

(14) કાપેલું અંતર

(15) ઝડપ

(16) જ્યારે ગતિ કરતા વાહન ઉપર બ્રેક લગાડવામાં આવે છે ત્યા૨ે તેમાં પ્રવેગ ઉત્પન્ન થાય છે, જે ઋણ હોય છે. (અર્થાત્ વાહન પ્રતિપ્રવેગી ગતિ કરે છે.)

(17) જો કોઈ ગતિમાન પદાર્થ (એક દિશામાં) સમયના એકસરખા ગાળામાં એકસરખું અંતર કાપતો ન હોય, તો તે પદાર્થ અનિયમિત ગતિ કરે છે તેમ કહેવાય.

(18) સ્થાનાંતર મૂલ્ય

પ્રશ્ન 2. ખાલી જગ્યા પૂરો : [પ્રત્યેકનો 1 ગુણ]

(1) 72 km h⁻¹ની અચળ ઝડપે ગતિ કરતી કારની ઝડપ ……… m/s છે.

(2) નિયમિત ગતિ કરતા એક પદાર્થના x−tના આલેખમાં મળતી સુરેખાનો ઢાળ …..… નું મૂલ્ય આપે છે.

(3) નિયમિત વર્તુળમય ગતિ કરતા પદાર્થની રેખીય ઝડપ શોધવા માટેનું સૂત્ર ……… છે.

(4) એક જ દિશામાં જતી એક બસની ઝડપ 20 sમાં 36 km h⁻¹થી વધીને 72 km h⁻¹ થાય છે, તો તેનો પ્રવેગ …….. m s^-2 હશે.

(5 ) સુરેખ પથ પર 20 m s⁻¹ની ઝડપે ગતિ કરતી બસમાં 4m s^-2 પ્રવેગ ઉત્પન્ન કરવામાં આવે, તો 2 s બાદ તેની ઝડપ ……. ms^-1 હશે.

(6) એક ઇલેક્ટ્રિક ટ્રેન 120 km h⁻¹ના અચળ વેગથી ગતિ કરે છે. તેણે 1 minuteમાં ……. km અંતર કાપ્યું હશે.

(7) એક ટ્રેન અમદાવાદથી વડોદરા જતાં 2 ક્લાકનો સમય લે છે. તે જ ટ્રેન વડોદરાથી અમદાવાદ પાછી ફરતાં 3 ક્લાકનો સમય લે છે. અમદાવાદ અને વડોદરા વચ્ચેનું અંતર 100 km છે, તો ટ્રેનની સરેરાશ ઝડપ ……. km h^-1 છે.

(8) એક ટ્રેન એક સ્ટેશનેથી ગતિની શરૂઆત કરી સુરેખ માર્ગ પર ‘s’ અંતર 30 km h⁻¹ની અચળ ઝડપે કાપે છે. ત્યારબાદ ત્યાંથી વિરુદ્ધ દિશામાં ગતિ કરી તેટલું જ અંતર 45 km h⁻¹ની અચળ ઝડપે કાપીને મૂળ સ્ટેશને પાછી આવે છે, તો તેનો સરેરાશ વેગ …….. હશે.

(9) કા૨ે કાપેલું અંતર કારમાં રહેલા ……… સાધનની મદદથી જાણી શકાય છે.

(10) એક મોટરસાઇક્લની પહેલી 10 મિનિટમાં ઝડપ 40 km h^-1 અને બીજી 10 મિનિટમાં 50 km h⁻¹ છે, તો આ મોટરસાઇકલની 20 મિનિટના સમયગાળા દરમિયાન સરેરાશ ઝડપ ……… km h^-1 છે.

ઉત્તર :

(1) 20

(2) ઝડપ

(3) v = 2πr/t

(4) 0.5

(5) 28

(6) 2

(7) 40

(8) શૂન્ય

(9) ઓડોમિટર

(10) 45

પ્રશ્ન 3. નીચેનાં વિધાનો ખરાં છે કે ખોટાં તે જણાવો : [પ્રત્યેકનો 1 ગુણ]

(1) ગતિ એ નિરપેક્ષ ખ્યાલ છે.

(2) અંતર અને સ્થાનાંતર બંને માટે SI એકમ મીટર છે.

(3) એક પદાર્થે કરેલ સ્થાનાંતરનું મૂલ્ય 20 m છે, તો તે પદાર્થે કાપેલું અંતર 20 m છે એમ કહી શકાય.

(4) આપેલ સમયગાળામાં પદાર્થે કાપેલું અંતર ધન, ઋણ અથવા શૂન્ય હોઈ શકે.

(5) પદાર્થે કરેલ સ્થાનાંતર શૂન્ય હોઈ શકે.

(6) સરેરાશ ઝડપ એ જુદી જુદી ઝડપની સરેરાશ છે.

(7) નિયમિત વર્તુળમય ગતિ કરતો પદાર્થ અચળ ઝડપે ગતિ કરે છે. તેથી તેનો વેગ અચળ હોય છે એમ કહેવાય.

(8) નિયમિત વર્તુળમય ગતિ કરતો પદાર્થ પ્રવેગી ગતિ કરે છે.

(9) એક પદાર્થે કાપેલા 120 km અંતર પૈકી અડધું અંતર 20 km h⁻¹ની ઝડપે અને બાકીનું અડધું અંતર 30 km h⁻¹ની ઝડપે કાપ્યું હોય, તો તેની સરાસરી ઝડપ 25 km h⁻¹ છે.

(10) એક ટ્રેન પ્રથમ 15 મિનિટ સુધી 40 km h⁻¹ની ઝડપે અને પછીની 15 મિનિટ સુધી 60 km h⁻¹ની ઝડપે ગતિ કરે છે, તો આ સમયગાળા દરમિયાન તેની સરાસરી ઝડપ 50 km h^-1 છે.

ઉત્તર :

(1) ખોટું

(2) ખરું

(3) ખોટું

(4) ખોટું

(5) ખરું

(6) ખોટું

(7) ખોટું

(8) ખરું

(9) ખોટું

(10) ખરું

પ્રશ્ન 4. નીચેના દરેક પ્રશ્ન માટે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરી ઉત્તર લખો : [પ્રત્યેકનો 1 ગુણ]

1. નીચેના પૈકી કઈ ભૌતિક રાશિને તેના મૂલ્યની સાથે દિશા દર્શાવવી જરૂરી છે?

A. ઝડપ

B. પથલંબાઈ

C. સ્થાનાંતર

D. તાપમાન

2. કોઈ દોડવીર 400mના પરિઘવાળા વર્તુળાકાર પથ પર એક ચક્કર પૂર્ણ કરે ત્યારે તેણે કેટલું સ્થાનાંતર કર્યું કહેવાય?

A. 400m

B. 200m

C. 100m

D. શૂન્ય

3. 54 km/hની અચળ ઝડપે ગતિ કરતી ટ્રેનની ઝડપ m s⁻¹ના એકમમાં કેટલી થાય?

A. 15ms^-1

B. 90ms^-1

C. 1.5ms^-1

D. 9ms^-1

4. એક સ્કૂટરસવાર 30kmh⁻¹ની અચળ ઝડપે સુરેખ માર્ગ પર સતત 20min ગતિ કરે, તો તેણે કુલ કેટલું અંતર કાપ્યું હશે?

A. 1.5km

B. 6km

C. 10km

D. 90km

5. એક સાઇકલસવા૨ પૂર્વ દિશામાં 5km અંતર કાપે છે. ત્યારબાદ તે દક્ષિણ દિશામાં 12km અંતર કાપે છે. આ સાઇકલસવા૨ે કરેલ સ્થાનાંતરનું મૂલ્ય કેટલું ?

A. 17km

B. 13km

C. 7km

D. શૂન્ય

6. જો ગતિમાન પદાર્થનો વેગ – સમયનો આલેખ સમયની અક્ષને સમાંતર એવી સુરેખા મળે, તો તે કેવી રીતે ગતિ કરતો હશે?

A. સ્થિર હશે

B. અનિયમિત

C. અચળ પ્રવેગી

D. અચળવેગી

7. આકૃતિમાં દર્શાવેલ આલેખ પદાર્થની કેવા પ્રકારની ગતિ દર્શાવે છે?

A. નિયમિત ગતિ

B. નિયમિત પ્રવેગી ગતિ

C. અનિયમિત પ્રવેગી ગતિ

D. સ્થિર

8. જો કોઈ વાહનનો વેગ 5 sમાં 5 m s⁻¹થી વધીને 15 ms^-1 થાય, તો તેના પ્રવેગનું મૂલ્ય કેટલું હશે?

A. 4m s^-2

B. 4ms^-1

C. 2ms^-1

D. 2ms^-2

9. ગતિમાન વાહનો A અને B માટે વેગ વિરુદ્ધ સમયના આલેખો આકૃતિમાં દર્શાવ્યા છે. કયું વાહન પ્રવેગી ગતિ કરે છે અને કયું વાહન પ્રતિપ્રવેગી (એટલે કે ઋણ પ્રવેગી) ગતિ કરે છે? 

A. વાહન A પ્રતિપ્રવેગી, વાહન B પ્રવેગી

B. વાહન A પ્રવેગી, વાહન B પ્રતિપ્રવેગી

C. વાહન A અને વાહન B બંને પ્રવેગી

D. વાહન A અને વાહન B બંને પ્રતિપ્રવેગી

10. એક ગતિમાન કારનો પ્રવેગ 1.5 m s⁻² છે. ચાર સેકન્ડ બાદ તેના વેગમાં કેટલો વધારો થયો હશે?

A. 6 m s⁻¹

B. 4 m s⁻¹

C. 3 m s⁻¹

D. 2.66 m s⁻¹

11. નીચેના પૈકી કઈ ભૌતિક રાશિને મૂલ્ય સાથે દિશા દર્શાવવી જરૂરી નથી?

A. ઝડપ

B. સ્થાનાંતર

C. વેગ

D. પ્રવેગ

12. પદાર્થ નિયમિત ગતિ કરે છે એમ ક્યારે કહેવાય?

A. સરખા સમયગાળામાં જુદું જુદું અંતર કાપતો હોય ત્યારે

B. જુદા જુદા સમયગાળામાં સરખું અંતર કાપતો હોય ત્યારે

C. સરખા સમયગાળામાં સરખું અંતર કાપતો હોય ત્યારે

D. જુદા જુદા સમયગાળામાં જુદું જુદું અંતર કાપતો હોય ત્યારે

13. એક વ્યક્તિ પોતાના ઘરેથી ઉત્તર દિશામાં 4 km અંતર ચાલે છે. ત્યાંથી તે 3 km અંતર પશ્ચિમ દિશામાં ચાલે છે. હવે, આ સ્થળેથી વ્યક્તિ લઘુતમ અંતરવાળા માર્ગે ચાલીને પોતાના ઘેર જાય છે. આ વ્યક્તિએ કાપેલું કુલ અંતર કેટલું થશે?

A. 5 km

B. 7 km

C. 12 km

D. શૂન્ય

14. એક વાહન સુરેખ પથ પર t સમયગાળામાં 20 kmh⁻¹ ની અચળ ઝડપે અમુક અંતર કાપે છે. બીજા તેટલા જ સમયગાળામાં 30 kmh⁻¹ ની અચળ ઝડપે અમુક અંતર કાપે છે, તો વાહનની સરેરાશ ઝડપ કેટલી?

A. 25 km h⁻¹

B. 24km h⁻¹

C. 50km h⁻¹

D. 12 km h⁻¹

15. પ્રવેગ એટલે શું?

A. એકમ સમયમાં કપાયેલું અંતર

B. એકમ સમયમાં થતું સ્થાનાંતર

C. એકમ સમયમાં થતો વેગનો ફેરફાર

D. એકમ સમયમાં થતો વેગમાનનો ફેરફાર

16. નિયમિત વર્તુળમય ગતિ કરતા પદાર્થ માટે શું અચળ હોય છે?

A. પ્રવેગ

B. વેગ

C. સ્થાનાંતર

D. ઝડપ

17. ગતિમાન પદાર્થ માટે તેના સ્થાનાંતર અને કાપેલા અંતરના ગુણોત્તરનું સંખ્યાત્મક મૂલ્ય …….

A. હંમેશાં 1 કરતાં નાનું હોય છે.

B. હંમેશાં 1 જેટલું હોય છે.

C. હંમેશાં 1 કરતાં વધુ હોય છે.

D. 1 જેટલું કે 1 કરતાં ઓછું હોઈ શકે છે.

18. જો પદાર્થે કાપેલું અંતર (s), સમય (t)ના વર્ગના સમપ્રમાણમાં હોય, તો તે પદાર્થ ……..

A. અચળ વેગથી ગતિ કરતો હશે.

B. અચળ પ્રવેગી ગતિ કરતો હશે.

C. વધતા પ્રવેગ સાથે ગતિ કરતો હશે.

D. ઘટતા પ્રવેગ સાથે ગતિ કરતો હશે.

19. નીચે દર્શાવેલી કયા પ્રકારની ગતિમાં પદાર્થે કાપેલું અંતર અને તેના સ્થાનાંતરનું મૂલ્ય સમાન હોઈ શકે છે?

A. એક કાર સુરેખ પથ પર ગતિ કરતી હોય.

B. એક કાર વર્તુળાકાર પથ પર ગતિ કરતી હોય.

C. એક દોલક મધ્યમાનસ્થાનની આસપાસ દોલન કરતું હોય.

D. સૂર્યની આસપાસ પૃથ્વી પરિક્રમણ કરતી હોય.

ઉત્તર :

1. સ્થાનાંતર

2. શૂન્ય

3. 15 m s^-1

4. 10km

5. 13km

6. અચળ વેગી

7. નિયમિત પ્રવેગી ગતિ

8. 2m s^-2

9. વાહન A પ્રવેગી, વાહન B પ્રતિપ્રવેગી

10. 6 m s^-1

11. ઝડપ

12. સરખા સમયગાળામાં સરખું અંતર કાપતો હોય ત્યારે.

13. 12km

14. 25 km h^-1

15. એકમ સમયમાં થતો વેગનો ફેરફાર

16. ઝડપ

17. 1 જેટલું કે 1 કરતાં ઓછું હોઈ શકે છે.

18. અચળ પ્રવેગી ગતિ કરતો હશે.

19. એક કાર સુરેખ પથ પર ગતિ કરતી હોય.

મૂલ્યો આધારિત પ્રશ્નોત્તર (Value Based Questions with Answers)

(1) એક હાઈવે પર મહત્તમ ઝડપ મર્યાદા 80 km h⁻¹ની દર્શાવેલી છે. એક કારચાલક આ હાઈવે પર (મહત્તમ મર્યાદાનું બોર્ડ જોયા વગર) કારને 100 km h⁻¹ની ઝડપે હંકારે છે. પરંતુ તેની બાજુમાં બેઠેલ વિજ્ઞાનશિક્ષક તેને કારની ઝડપ ઘટાડીને 80 km h^-1 કરવાની સલાહ આપે છે. કારચાલક સલાહનું પાલન કરે છે. હવે અચાનક કારથી 55 mના અંતરે એક હૅન્ડિકૅપ વ્યક્તિ આ હાઈવેને ઓળંગવાનો પ્રયત્ન કરે છે. તેને જોઈને કારચાલક તરત જ જોરથી બ્રેક લગાડીને કારમાં 5m s⁻²નો પ્રતિપ્રવેગ ઉત્પન્ન કરે છે, તો

(a) શું અકસ્માત નિવારી શકાશે?

(b) વિજ્ઞાનશિક્ષકની સલાહ કારચાલકે માની ન હોત તો શું થાત?

(c) કારચાલક અને વિજ્ઞાનશિક્ષકનાં મૂલ્યો જણાવો.

ઉત્તર:

(a) બ્રેક માર્યા પછી કાર સ્થિર થાય ત્યાં સુધીમાં કારે કાપેલું અંતર નીચે મુજબ ગણી શકાય :

(c) કાર ચાલકનાં મૂલ્યો : આજ્ઞાંકિત

વિજ્ઞાનશિક્ષકનાં મૂલ્યો : નિયમ-પાલનતા, ભૌતિક વિજ્ઞાનનું બહોળું પ્રાયોગિક જ્ઞાન અને બીજા માટેનું કાળજીભર્યું વલણ.

(2) પૂજા અને તેની બહેનપણી સાનિયા એક કારમાં પોતાની સ્કૂલમાં જાય છે. પૂજા વિજ્ઞાનપ્રવાહની વિદ્યાર્થિની છે અને સાનિયા વાણિજ્ય પ્રવાહની વિદ્યાર્થિની છે. સાનિયા કારના ડ્રાઇવરને કારની ઝડપ વધારવાની સૂચના આપે છે. પૂજા તેનો વિરોધ કરે છે અને સાનિયાને સમજાવે છે કે શાળાએ પહોંચવાનો સમય સરેરાશ ઝડપ પર આધાર રાખે છે. કારની ઝડપ થોડાક સમય માટે વધારીને ખોટું જોખમ વધારવાની જરૂર નથી.

ઉપરનો ફકરો વાંચીને નીચેના પ્રશ્નોના જવાબ આપો :

(a) પૂજાનાં કર્યાં મૂલ્યો છતાં થાય છે?

(b) શું. પૂજાએ કરેલો વિરોધ સાચો છે?

(c) તમે સરેરાશ ઝડપ કયા સૂત્ર વડે રજૂ કરશો?

ઉત્તર :

(a) વ્યાપકરૂપે બીજા ડ્રાઇવરો માટે અને ચોક્કસપણે તેની બહેનપણી માટે કાળજી અને સુરક્ષાની ભાવના છતી કરે છે.

(b) હા. પુજાએ કરેલો વિરોધ સાચો છે.

(c) સરેરાશ ઝડપ = કાપેલું કુલ અંતર/તે કુલ અંતર કાપવા માટે લાગતો કુલ સમય

(3) બે મિત્રો અમિત અને રાઘવ પોતપોતાની બાઇક લઈને કૉલેજ પર જતા હોય છે. એક વખત ચાર રસ્તા પર ખૂબ ટ્રાફિક જામ થાય છે. તેથી અમિત લાલ સિગ્નલ તોડીને અતિઝડપે બાઇક ચલાવીને કૉલેજ પર વહેલો પહોંચે છે. અમિત અને રાઘવ માટે અંતર – સમયના આલેખ એક જ આલેખપત્ર પર નીચે દર્શાવ્યા છે :

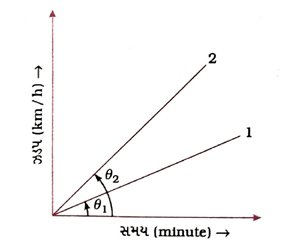
(a) ઝડપ – સમયનો કયો આલેખ અમિત માટેનો હશે?

(b) અમિત અને રાઘવનાં કયાં મૂલ્યો છતાં થાય છે?

(c) રાઘવે અમિતને કઈ સલાહ-સમજણ આપવી જોઈએ?

ઉત્તર :

(a) આલેખ – 2, કારણ કે આલેખ – 2નો ઢાળ, આલેખ – 1 કરતાં વધુ છે.

(b) અમિતનાં મૂલ્યો : બેકાળજીભર્યું વર્તન, ઉતાવળિયો સ્વભાવ, કાયદાનું પાલન ન કરનાર.

રાઘવનાં મૂલ્યો : કાયદાનું ચુસ્ત પાલન કરનાર, બીજાની દરકાર કરનાર, સહનશીલ.

(c) આપણે સમાજના હિત માટે કાયદાનું ચુસ્ત પાલન કરવું જોઈએ અને બેદરકારીભર્યું વર્તન સુધારવું જોઈએ. જેથી કરીને પોતાનું અને સમાજનું સારું થાય.

हमसे जुड़ें, हमें फॉलो करे ..

• Telegram ग्रुप ज्वाइन करे – Click Here
• Facebook पर फॉलो करे – Click Here
• Facebook ग्रुप ज्वाइन करे – Click Here
• Google News ज्वाइन करे – Click Here