NCERT Solutions Class 9Th Math – रचनाएँ
NCERT Solutions Class 9Th Math – रचनाएँ
लघु उत्तरीय प्रश्नोत्तर
रचनाएँ
1. एक दी हुई किरण के प्रारंभिक बिंदु पर 90° के कोण की रचना करें और कारण सहित रचना की पुष्टि करें।
हल – रचना के चरण
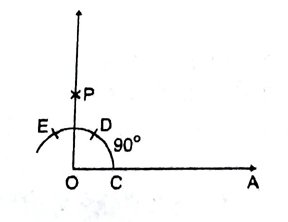
(i) किरण OA खींचा।
(ii) इसके आरंभिक बिंदु को केन्द्र मानकर किसी भी त्रिज्या का एक चाप CDE खींचा जो OA को C पर काटता है।
(iii) C को केन्द्र मानकर समान त्रिज्या का चाप खींचा जो चाप CDE को D पर काटता है।
(iv) D को केन्द्र मानकर समान त्रिज्या का चाप खींचा जो CDE को E पर काटता है।
(v) D और E को केन्द्र मानकर, सुविधाजनक त्रिज्या (½DE से अधिक) और दो चाप काटें जो एक-दूसरे को P बिंदु पर काटा ।
(vi) OP को मिलाएँ । इस प्रकार ∠AOP = 90⁰

2. एक दी हुई किरण के प्रारंभिक बिंदु पर 450 के कोण की रचना करें और कारण सहित रचना की पुष्टि करें।
हल – रचना के चरण
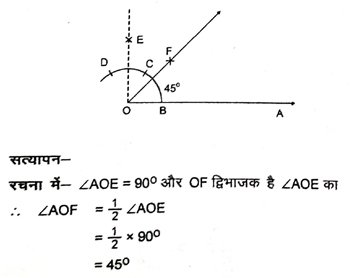
(i) किरण OA खींचा।
(ii) O को केन्द्र मानकर किसी भी सुविधाजनक त्रिज्या का एक चाप खींचा, जो OA को B बिंदु पर काटता ।
(iii) B को केन्द्र मानकर समान त्रिज्या का चाप खींचा जो C पर काटे ओर फिर C को केन्द्र से मानकर समान त्रिज्या का चाप खींचा जो D पर काटे ।
(iv) C केन्द्र से CD की आधी से अधिक त्रिज्या लेकर एक चाप खींचा।
(v) D केन्द्र से समान त्रिज्या का दूसरा चाप खींचा जो पिछले चाप को E पर काटे ।
(vi) OE को मिलाएँ । इस प्रकार ∠AOE = 90⁰
(vii) ∠AOE का द्विभाजक OF खींचा। इस प्रकार ∠AOF = 45⁰
3. निम्न मापों के कोणों की रचना करें-
(a) 30° (b) 22½° (c) 15°
हल – (a) रचना के चरण –
(i) किरण OA खींचा।
(ii) इसके आरंभिक बिंदु को केन्द्र मानकर किसी भी त्रिज्या का एक चाप खींचें जो OA को B पर काटता है।
(iii) B को केन्द्र मानकर समान त्रिज्या का एक चाप खींचा जो मानकर C पर काटा ।
(iv) B और C केन्द्र से किसी भी सुविधाजनक त्रिज्या ( ½BC से अधिक) वाले दो चाप खींचा जो परस्पर D पर काटा।
(v) OD को मिलाया । इस प्रकार ∠AOD = 30°

4. निम्न कोणों की रचना करें और चाँद द्वारा मापकर पुष्टि करें –

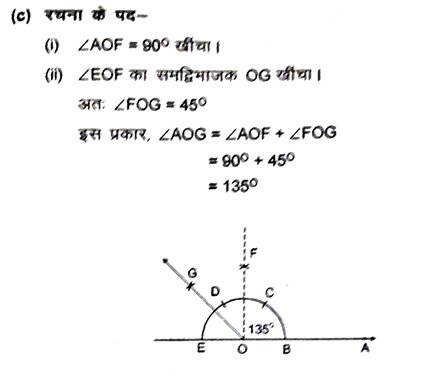
5. एक समबाहु त्रिभुज की रचना करें, जब इसकी भुजा दी हो तथा कारण सहित रचना करें ।
हल – रचना के चरण-
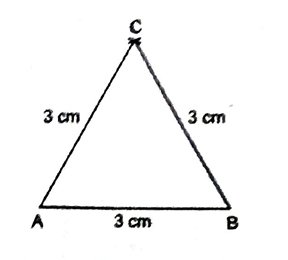
(i) AB = 3 सेमी खींचा।
(ii) A और B को केन्द्र मानकर AB = 3 सेमी त्रिज्या के दो चाप काटे जो परस्पर C पर काटते हैं ।
(iii) AC और BC को मिलाया ।
इस प्रकार, ABC अभीष्ट समबाहु त्रिभुज है।
सत्यापन – चूँकि रचना द्वारा AB = BC = CA = 3 सेमी
∴ Δ ABC एक समबाहु त्रिभुज है ।
6. एक त्रिभुज ABC की रचना करें, जिसमें BC = 7 सेमी, B = 75⁰ सेमी और AB + AC = 13 सेमी हो ।
हल- रचना के चरण-
(i) एक किरण BX खींचा। इसमें से एक रेखाखंड BC = 7 सेमी काटा।
(ii) ∠XBY = 75° बनाया ।
(iii) BY से BD = 13 सेमी काटा ।
(iv) CD को मिलाएँ ।
(v) CD का लंब समद्विभाजक RS खींचा जो BY को A बिंदु पर प्रतिच्छेदित करता है।
(vi) AC को मिलाया ।
इस प्रकार ABC एक त्रिभुज प्राप्त होता है।

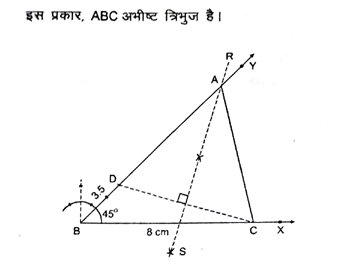
7. एक त्रिभुज ABC की रचना करें, जिसमें BC = 8 सेमी, ∠B = 45° और AB – AC = 3.5 सेमी हो ।
हल – रचना के चरण-
(i) एक किरण BX खींचें और इसमें से एक रेखाखंड BC = 8 सेमी काटा।
(ii) ∠YBC = 45° बनाया ।
(iii) BY से BD = 3.5 सेमी का रेखाखंड काटा ।
(iv) CD को मिलाया ।
(v) CD का लंब समद्विभाजक RS खींचा जो BY को A बिंदु पर प्रतिच्छेदित करता है।
(vi) AC को मिलाया ।
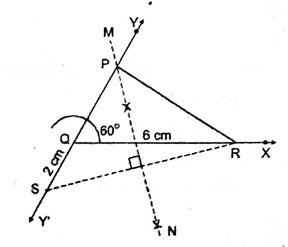
8. एक त्रिभुज PQR की रचना करें, जिसमें QR = 6 सेमी, ∠Q = 600 और PR – PQ = 2 सेमी हो ।
हल- रचना के चरण –
(i) एक किरण QX खींचा उनमें से एक रेखाखंड QR = 6 सेमी काटा।
(ii) QR से 60° का कोण बनाते हुए किरण QY खींचें और YQ को YQY’ तक आगे बढ़ाया।
(iii) QY से एक रेखाखंड QS = 2 सेमी काटा ।
(iv) RS का मिलाया ।
(v) RS का लंब समद्विभाजक MN खींचे जो QY को बिन्दु P पर प्रतिच्छेदित करता है ।
(vi) PR को मिलाया ।
इस प्रकार, PQR एक अभीष्ट त्रिभुज है ।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here