NCERT Solutions Class 9Th Math – वृत्त
NCERT Solutions Class 9Th Math – वृत्त
लघु उत्तरीय प्रश्नोत्तर
वृत्त
1. आकृति में केन्द्र O वाले एक वृत्त पर तीन बिंदु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60⁰ है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है, तो ∠ADC ज्ञात करें।
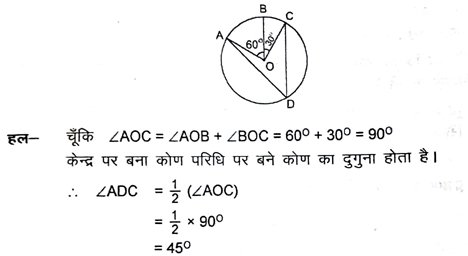
2. किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात करें तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात करें ।
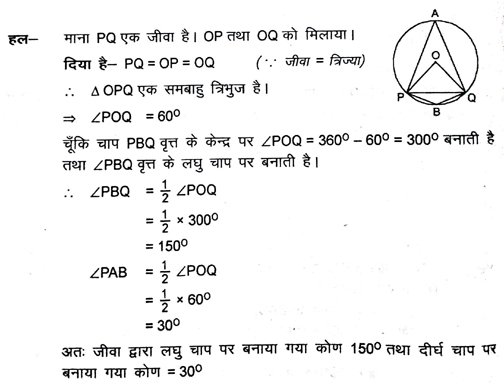
3. आकृति में, ∠PQR = 1000 है, जहाँ P, Q तथा R, केन्द्र O वाले एक वृत्त पर स्थित बिंदु हैं। ∠OPR ज्ञात करें ।

4. आकृति में, ∠ABC = 690° और ∠ACB = 31° हो, तो ∠BDC ज्ञात करें।
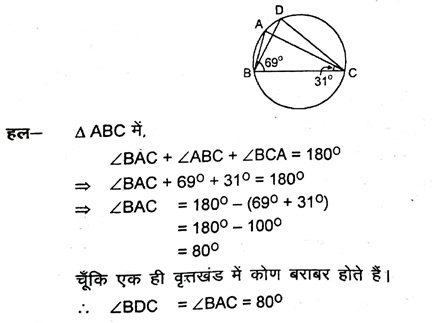
5. आकृति में, एक वृत्त पर A, B, C और D चार बिंदु हैं। AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130⁰ तथा ∠ECD = 20⁰है। ∠BAC ज्ञात करें।
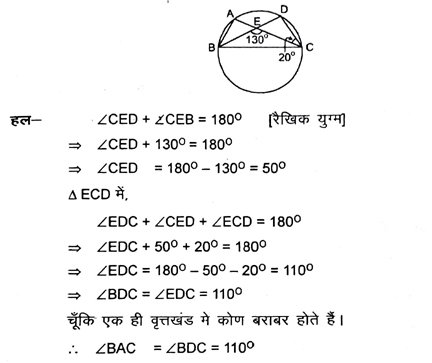
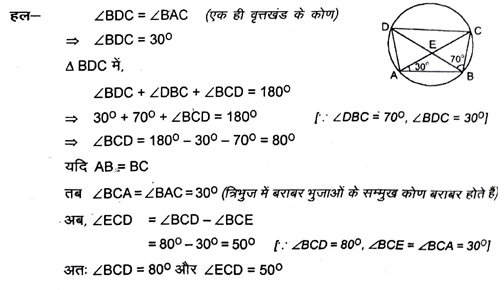
6. ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिंदु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात करें। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात करें ।
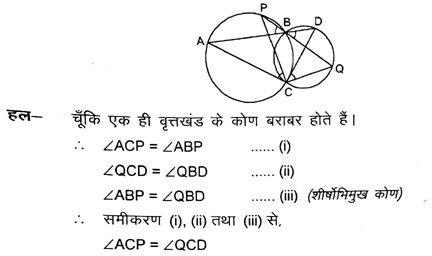
7. दो वृत्त दो बिंदुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखंड ABD और PBQ वृत्तों को A, D और P, Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गए हैं (देखें आकृति) । सिद्ध करें कि ∠ACP = ∠QCD है।
8. यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध करें कि इन वृत्तों का प्रतिच्छेद बिंदु तीसरी भुजा पर स्थित है।
हल – दिया है- Δ ABC की भुजाएँ AB तथा AC को व्यास लेते हुए दो वृत्त बनाए गए हैं। वृत्त एक दूसरे को A तथा D बिंदु पर प्रतिच्छेदित करते हैं।
सिद्ध करना है- D, BC पर स्थित है।
रचना– A तथा D को मिलाया ।
प्रमाण- चूँकि AB तथा AC दो वृत्तों के व्यास हैं।

9. उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध करें कि ∠CAD = ∠CBD है।

दीर्घ उत्तरीय प्रश्नोत्तर
वृत्त
1. याद करें कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध करें कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करती हैं।

2. सिद्ध करें कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अंतरित करें, तो जीवाएँ बराबर होती हैं ।

3. यदि दो वृत्त परस्पर दो बिंदुओं पर प्रतिच्छेद करें, तो सिद्ध करें कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब समद्विभाजक पर स्थित हैं।
हल – दिया है- दो वृत्त जिनके केन्द्र तथा O’ हैं। दो बिंदुओं A तथा B पर इस प्रकार प्रतिच्छेद करते हैं कि AB दोनों वृत्तों की उभयनिष्ठ जीवा है तथा 00′ एक रेखाखंड है जो कि वृत्तों के केन्द्र को मिलाती है।
माना कि OO’, AB को M पर प्रतिच्छेद करती है ।
सिद्ध करना है- OO’ AB का लम्ब समद्विभाजक है ।
रचना – रेखाखंड OA, OB, O’A तथा O’B खींचा l

4. 5 सेमी तथा 3 सेमी त्रिज्या वाले दो वृत्त दो बिंदुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 सेमी है। उभयनिष्ठ जीवा की लम्बाई ज्ञात करें ।

5. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध करें कि एक जीवा के दोनों खंड दूसरे जीवा के संगत खंडों के बराबर हैं।
हल – दिया है— AB तथा CD वृत्त की जीवाएँ हैं, O वृत्त का केन्द्र है। AB तथा CD, P पर प्रतिच्छेद करते हैं और AB = CD

6. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध करें कि प्रतिच्छेद बिंदु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
हल – दिया है— AB तथा CD वृत्त की जीवाएँ हैं, O वृत्त का केन्द्र है। AB तथा CD, P पर प्रतिच्छेद करते हैं तथा AB = CD


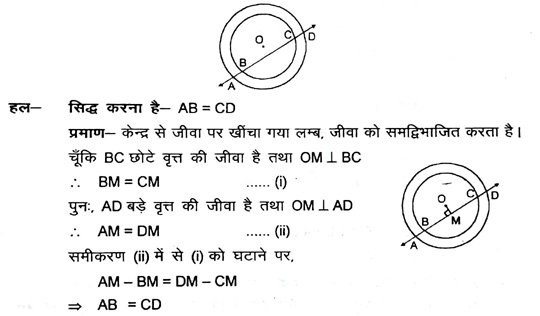
7. यदि एक रेखा दो संकेद्री वृतों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध करें AB = CD है (देखें आकृति) ।
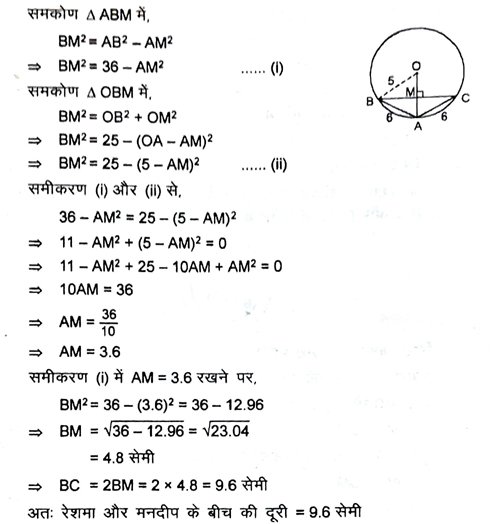
8. एक पार्क में बने 5 मी त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच-और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 मी हो, तो रेशमा और मनदीप के बीच की दूरी क्या है ?
हल – माना कि तीनों लड़कियाँ रेशमा, सलमा और मनदीप क्रमशः 5 सेमी की त्रिज्या वाले वृत्त पर बिंदु B, A तथा C पर खड़ी हैं ।
AB तथा AC एक वृत्त की दो समान जीवाएँ हैं तब वृत्त का केन्द्र ∠BAC के समद्विभाजक पर स्थित होगा ।
यहाँ AB = AC = 6 सेमी अर्थात् OA, ∠BAC का समद्विभाजक है।
∴ M, BC का मध्य बिंदु है ।
⇒ OM ⊥ BC
9. 20 मी त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात करें।


10. यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध करें कि वह एक आयत है।
हल – एक चक्रीय चतुर्भुज के विकर्ण AC तथा BD एक ही वृत्त के व्यास हैं जो चतुर्भुज ABCD के शीर्ष A, B, C तथा D हैं |
सिद्ध करना है- चतुर्भुज ABCD एक आयत है ।
प्रमाण- चूँकि एक वृत्त की सभी त्रिज्याएँ बराबर होती हैं ।

प्रमेय (वृत्त)
1. सिद्ध करें कि वृत्त की बराबर जीवाएँ केंद्र पर बराबर कोण अंतरित करती हैं |

2. सिद्ध करें कि यदि वृत्त की जीवाओं द्वारा केंद्र पर अंतरित कोण बराबर हों, तो जीवा बराबर होती हैं ।


3. सिद्ध करें कि वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है ।

4. सिद्ध करें कि वृत्त के केंद्र और जीवा के मध्य बिंदु को मिलाने वाली रेखा जीवा पर लंब होती है।
हल – दिया है – वृत्त C (O, r) की जीवा AB है जिसका मध्य बिंदु P है। OP को मिलाया गया है।

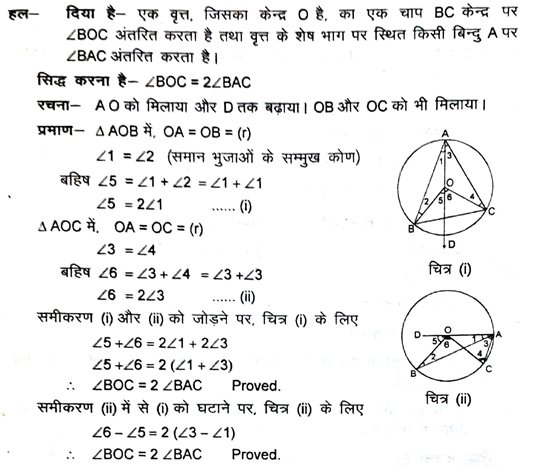
5. सिद्ध करें कि किसी चाप द्वारा केन्द्र पर अंतरित कोण उस चाप द्वारा वृत्त के शेष भाग पर स्थित किसी बिन्दु पर अंतरित कोण का दुगुना होता है।
6. सिद्ध करें कि एक ही वृतखंड के कोण बराबर होते हैं।

हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here