NCERT Solutions Class 9Th Math – यूक्लिड की ज्यामिति का परिचय
NCERT Solutions Class 9Th Math – यूक्लिड की ज्यामिति का परिचय
लघु उत्तरीय प्रश्नोत्तर
1. निम्नांकित कथनों में से कौन-से कथन सत्य हैं और कौन-से कथन असत्य हैं ? अपने उत्तरों के लिए कारण दें –
(i) एक बिंदु से होकर केवल एक ही रेखा खींची जा सकती है।
हल – असत्य ।
एक कागज पर एक बिंदु P अंकित करें । एक पेन्सिल तथा स्केल की सहायता से एक रेखा / उससे होकर गुजरती हुई बनाएँ। एक और रेखा mP से होकर गुजरती हुई बनाएँ । इस प्रक्रिया को लगातार करें । हम जितनी चाहें उतनी रेखाएँ P से होकर गुजरती हुई बना सकते हैं।
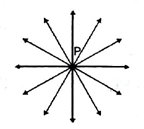
(ii) दो भिन्न बिंदुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
हल – असत्य ।
एक कागज पर दो बिंदु A तथा B अंकित करें । कागज को इस प्रकार मोड़े कि एक क्रीज बिंदु A से होकर गुजरे जैसा कि भाग (i) में दिखाया गया है । एक बिंदु से असीमित रेखाएँ गुजर सकती हैं।
पुनः कागज को इस प्रकार मोड़ें कि एक क्रीज B से होकर गुजरे । स्पष्ट रूप से B से असीमित रेखाएँ गुजर सकती हैं। हम यह पाते हैं कि यहाँ पर केवल एक ही रेखा है जो कि A तथा B से होकर गुजरती है। इसलिए दो बिंदुओं से होकर केवल एक ही रेखा गुजर सकती है।
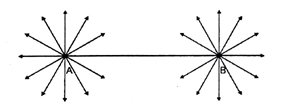
(iii) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है।
हल – सत्य ।
नोट करें कि जिसे आजकल हम एक रेखाखंड कहते हैं, यूक्लिड ने उसे एक निरस्त रेखा कहा था ।
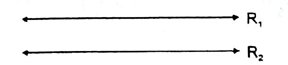
ज्यामिति में एक रेखा का मतलब रेखा की पूर्णता से, न कि उसका यह कोई हिस्सा है। पूर्ण रेखा का कोई भौतिक उदाहरण संभव नहीं है क्योंकि एक रेखा दोनों दिशाओं में अनंत तक जाती है इसलिए इसको पूर्ण रूप से एक कागज पर नहीं खींचा जा सकता है।
अभ्यास में रेखा का केवल एक हिस्सा खींचा जा सकता है और इस पर दो चिह्न लगाकर इसके अंत बिंदुओं को दोनों दिशाओं में दर्शाया जाता है। जैसा कि आकृति में दर्शाया गया है।

(iv) यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
हल – सत्य
एक वृत्त द्वारा घेरे गए क्षेत्र को यदि एक दूसरे वृत्त पर डाला जाए, तो वे वृत्त सम्पाती होते हैं तब उनके केंद्र तथा सीमाएँ भी सम्पाती होंगी। इसलिए उनकी त्रिज्याएँ भी बराबर होंगी।
(v) आकृति में, यदि AB = PQ और PQ = XY है, तो AB = XY होगा ।

हल – सत्य ।
क्योंकि चीजें जो एक ही चीज के बराबर हों, एक दूसरे के बराबर होती हैं।
2. निम्नांकित पदों में से प्रत्येक की परिभाषा दें-
(i) समांतर रेखाएँ, (ii) लम्ब रेखाएँ, (iii) रेखाखंड, (iv) वृत्त की त्रिज्या, (v) वर्ग ।
हल – (i) समांतर रेखाएँ- दो रेखाएँ समांतर रेखाएँ कहलाती हैं। जब (a) वे प्रतिच्छेद न करें, (b) जब वे समतलीय हों ।
(ii) लम्ब रेखाएँ – दो रेखाएँ AB तथा CD जो एक ही तल में स्थित हों, लम्ब रेखाएँ कहलाती हैं, यदि वे समकोण बनाएँ । हम लिखते हैं— AB I CD.

(iii) रेखाखंड – एक रेखाखंड रेखा का वह भाग होता है जब दो विभिन्न बिंदु A तथा B एक रेखा पर दिए गए हैं, तब रेखा का भाग जिसके अन्तः बिंदु A तथा B हों रेखाखंड कहलाती है।
इसे AB कहा जाता है | AB तथा BA एक ही रेखाखंड को दर्शाते हैं ।

(iv) वृत्त की त्रिज्या – केंद्र से वृत्त पर एक बिंदु की दूरी वृत्त की त्रिज्या कहलाती है।
या, केन्द्र से वृत्त पर स्थित किसी वस्तु की दूरी खिज्या कहलाती है।
(v) वर्ग– वह चतुर्भुज जिसकी चारों भुजाएँ बराबर हो तथा प्रत्येक कोण समकोण हो, वर्ग कहलाता है।
3. यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थिति है कि AC = BC है, तो सिद्ध करें कि AC = ½ AB है। एक आकृति खींच कर इसे स्पष्ट करें।
हल – हमारे पास एक बिंदु C है जो कि दो बिंदुओं A तथा B के बीच में इस प्रकार स्थित है कि AC = BC
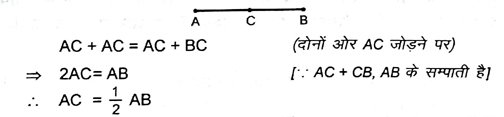
4. हलप्रश्न 3 में, C रेखाखंड AB का एक मध्य बिंदु कहलाता है। सिद्ध करें कि एक रेखाखंड का एक और केवल एक ही मध्य बिंदु होता है ।

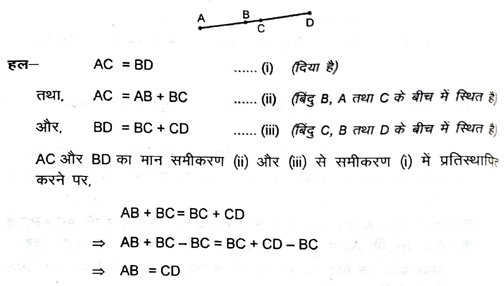
5. आकृति में, यदि AC = BD है, तो सिद्ध करें कि AB = CD है ।
6. युक्लिड की अभिगृहितों की सूची में दिया हुआ अभिगृहीत 5 एक सर्वव्यापी सत्य क्यों माना जाता है ? (ध्यान दें कि यह प्रश्न पाँचवीं अभिधारणा से संबंधित नहीं है।)
हल – युक्लिड की अभिगृहितों की सूचीं में दिया हुआ अभिगृहीत ब्रह्मांण की किसी भी चीज क लिए सत्य है । अतः यह सदैव सत्य है ।
7. आप युक्लिड की पाँचवी अभिधारणा को किस प्रकार लिखेंगे ताकि वह सरलता से समझी जा सके ?
हल – अभिगृहीत 2 तथ्यों का प्रयास
(i) P से गुजरती हुई एक रेखा है जो कि / के समांतर है।
(ii) ऐसी केवल एक ही रेखा है ।
8. क्या युक्लिड की पाँचवी अभिधारणा से समांतर रेखाओं के अस्तित्व का औचित्य निर्धारित होता है ? स्पष्ट करें।
हल – यदि एक सीधी रेखा , दो सीधी रेखाओं m तथा n पर इस प्रकार मिलती कि आंतरिक कोणों का योग दो समकोण / भुजा के एक ओर हो तो युक्लिड के पाँचवें अभिगृहीत के अनुसार रेखाएँ / के इस ओर नहीं मिलेंगी।
हम जानते हैं कि । के दूसरी ओर आंतरिक कोणों का योग भी दो समकोण होगा। इसलिए वे रेखाएँ इस ओर भी वहीं मिलेंगी। अतः ये कभी भी नहीं मिलेंगी इसलिए ये समांतर हैं ।
हमसे जुड़ें, हमें फॉलो करे ..
- Telegram ग्रुप ज्वाइन करे – Click Here
- Facebook पर फॉलो करे – Click Here
- Facebook ग्रुप ज्वाइन करे – Click Here
- Google News ज्वाइन करे – Click Here